Rizo (matemáticas)

Depiction of a two-dimensional vector field with a uniform curl.

En cálculo vectorial, el rotación es un operador vectorial que describe la circulación infinitesimal de un campo vectorial en el espacio euclidiano tridimensional. El rotacional en un punto del campo está representado por un vector cuya longitud y dirección denotan la magnitud y el eje de la circulación máxima. El rotacional de un campo se define formalmente como la densidad de circulación en cada punto del campo.

Un campo vectorial cuyo rotacional es cero se llama irrotacional. El rotacional es una forma de diferenciación para campos vectoriales. La forma correspondiente del teorema fundamental del cálculo es Stokes' teorema, que relaciona la integral de superficie del rotacional de un campo vectorial con la integral de línea del campo vectorial alrededor de la curva límite.

Curl F es una notación común hoy en los Estados Unidos y América. En muchos países europeos, particularmente en la literatura científica clásica, se usa tradicionalmente la notación alternativa rot F, que se escribe como "rotor", y proviene de la "tasa de rotación", que representa. Para evitar confusiones, los autores modernos tienden a utilizar la notación de productos cruzados con el operador del (nabla) ∇ × F, que también revela la relación entre curl (rotor), divergencia y operadores de gradiente.

A diferencia del gradiente y la divergencia, el rotacional tal como se formula en el cálculo vectorial no se generaliza simplemente a otras dimensiones; son posibles algunas generalizaciones, pero solo en tres dimensiones el rizo geométricamente definido de un campo vectorial vuelve a ser un campo vectorial. Esta deficiencia es consecuencia directa de las limitaciones del cálculo vectorial; por otro lado, cuando se expresa como un campo tensorial antisimétrico a través del operador de cuña del cálculo geométrico, el rotacional se generaliza a todas las dimensiones. La desafortunada circunstancia es similar a la del producto vectorial tridimensional y, de hecho, la conexión se refleja en la notación ∇× para el rotacional.

El nombre "rizo" fue sugerido por primera vez por James Clerk Maxwell en 1871, pero aparentemente el concepto fue utilizado por primera vez en la construcción de una teoría del campo óptico por James MacCullagh en 1839.

Definición

Los componentes F en posición r, normal y tangente a una curva cerrada C en un plano, encerrando un área de vectores plano ${displaystyle mathbf {A} =Amathbf {hat {n}$.

Regla de la mano derecha

Convención para la orientación vectorial de la línea integral

El pulgar apunta en la dirección ${displaystyle mathbf {hat {n}$ y los dedos se curvan a lo largo de la orientación de C

La curvatura de un campo vectorial F, denotada por curl F< /span>, o ∇ × F, o rot F, es un operador que asigna funciones Ck en R³ a C^k−1 funciones en R³, y en particular, mapea funciones continuamente diferenciables R³ → R³ a funciones continuas R³ → R³. Se puede definir de varias formas, a mencionar a continuación:

Una manera de definir el borde de un campo vectorial en un punto es implícitamente a través de sus proyecciones sobre varios ejes que pasan por el punto: ${displaystyle mathbf {ha}$ es cualquier vector de unidad, la proyección del rizo de F sobre ${displaystyle mathbf {ha}$ puede definirse como el valor límite de una línea cerrada integral en un plano ortogonal a ${displaystyle mathbf {ha}$ dividido por el área cerrada, ya que el camino de la integración se contrae indefinidamente alrededor del punto.

Más específicamente, el rizo se define en un punto p como

${displaystyle (nabla times mathbf {F})(p)cdot mathbf {hat {u} {overset {underset {mathrm {def} {}{} {} {}}}lim _{Ato 0}{}{}{}{} {} {}}} {}}}} {}}}}}}}} {}}} {}} {} {} {}}} {}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm} {mm} {m} {m} {mmmm} {mm} {mm} { {1} {fnK}oint} ¿Qué? {F} cdot mathrm {d} mathbf {r}$

donde la línea integral se calcula a lo largo del límite C de la zona A en cuestión, SilencioASilencio siendo la magnitud de la zona. Esta ecuación define la proyección del rizo de F sobre ${displaystyle mathbf {ha}$. Las superficies infinitesimal atadas por C han tenido ${displaystyle mathbf {ha}$ como su normalidad. C se orienta a través de la regla de la mano derecha.

La fórmula anterior significa que la proyección del rotacional de un campo vectorial a lo largo de cierto eje es la densidad de área infinitesimal de la circulación del campo proyectado sobre un plano perpendicular a ese eje. Esta fórmula no define a priori un campo vectorial legítimo, ya que las densidades de circulación individuales con respecto a varios ejes a priori no necesitan relacionarse entre sí de la misma manera que componentes de un vector do; que realmente se relacionen entre sí de esta manera precisa debe probarse por separado.

A esta definición se ajusta naturalmente el teorema de Kelvin-Stokes, como fórmula global correspondiente a la definición. Iguala la integral de superficie del rotacional de un campo vectorial a la integral de línea anterior tomada alrededor del límite de la superficie.

Otra forma en que se puede definir el vector rotacional de una función F en un punto es explícitamente como el valor límite de una integral de superficie con valor vectorial alrededor de un caparazón que encierra p dividido por el volumen encerrado, ya que el caparazón se contrae indefinidamente alrededor de p< /i>.

Más específicamente, el rizo puede definirse mediante la fórmula vectorial

${displaystyle (nabla times mathbf {F})(p){overset {compset {mathrm {def} {}{} {} {}}}lim _{Vto 0}{f}{} {f} {fn}}}}m}}m} {c}} {f}}} {fn}}} {fn}}}}}}}}}m}m}}m}m}m} {m}}} {m} {m}}}}}}}}}} {m}}}} {m}}} {m}} {m}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}mmmmmmmm}}mmmmmmmmmmmm}}}}}}}}}}}}}}}m}}}}}}}}}mm}}}mm}} {1} {fn}oint} ¿Qué? times mathbf {F} mathrm {d} S}$

donde la superficie integral se calcula a lo largo del límite S del volumen V, SilencioVSilencio siendo la magnitud del volumen, y ${displaystyle mathbf {hat {n}$ señalando hacia fuera desde la superficie S perpendicularmente en cada punto S.

En esta fórmula, el producto vectorial en el integrando mide la componente tangencial de F en cada punto de la superficie S, junto con la orientación de estas componentes tangenciales con respecto a la superficie S. Por lo tanto, la integral de superficie mide la extensión total en la que F circula alrededor de S< /span>, junto con la orientación neta de esta circulación en el espacio. El curl de un campo vectorial en un punto es entonces la densidad de volumen infinitesimal de la circulación neta vector (es decir, tanto la magnitud como la orientación espacial) del campo alrededor del punto.

A esta definición se ajusta naturalmente otra fórmula global (similar al teorema de Kelvin-Stokes) que iguala la integral de volumen del rotacional de un campo vectorial a la integral de superficie anterior tomada sobre el límite del volumen.

Mientras que las dos definiciones anteriores del rizo no tienen coordenadas, hay otra "fácil de memorizar" definición del rizo en coordenadas ortogonales curvilíneas, p. en coordenadas cartesianas, esféricas, cilíndricas, o incluso elípticas o parabólicas:

$${displaystyle {begin{aligned} {F}_{1}={frac {fnK} {fnMicroc {partial (h_{3}F_{3}}}}{partial {f}} {f}}} {f}}}} {f}} {f}}} {f}}}}} {f}}} {f}}}} {f}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}} {m}}} {m}}}}} {m}}}}} {m}}}}}}}}}}}}}} {m}}}}}}} {m}}}}}}}}}}}}}}}} u_{2}} {frac {partial (h_{2}F_{2}}{partial u_{3}}}}right),\[5pt] {F}_{2}={frac {fnK} {fnMicroc {partial (h_{1}F_{1}}}}{partial {f}} {f}}} {f}}}}} {fn0}}}}} {f}}}} {f}}}}} {f}}} {f}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}} {m}}} {m}}} {m} {m} {m}}}}}}}}}} {m}}}}}}}}}}}}}} {m}}}}}} {m}}}}}}}}}}}}}} { u_{3}}-{frac {partial (h_{3}F_{3}}{partial u_{1}}}}right),\[5pt] {F}_{3}={frac {fnK} {fnMicroc {partial (h_{2}F_{2}}}}{partial {f} {f}}} {f}}}} {f}} {f}}}} {f}}}} {f}} {f}}}}} {f}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}} {m} {m}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}} {m}}} {m} {m}}}}}}}}}} {m} {m}}}} {m}}}}} {m}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}}}} {fnMicros {fnMicrosoft Sans Serif}}} {fnMicrosoft Sans Serif}}} {f}}} {fnMicroc}}} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}mmmmmmmmmf}}}}}}}}}}}}}}}}}}}}mmf}}}mf}}}}}}}$$

La ecuación para cada componente (curl F)_k se puede obtener mediante intercambiando cada ocurrencia de un subíndice 1, 2, 3 en permutación cíclica: 1 → 2, 2 → 3 y 3 → 1 (donde los subíndices representan los índices relevantes).

Si (x₁, x₂, x₃) son las coordenadas cartesianas y (u₁, < i>u₂, u₃) son las coordenadas ortogonales, entonces

$${displaystyle h_{i}={sqrt {left({frac {partial ###### {fnMicroc {fnMicroc {fnMicroc {fnMicrosoft Sans Serif} {fnMicroc {fnMicrosoft Sans Serif} ################################################################################################################################################################################################################################################################ ¿Qué?$$

Interpretación intuitiva

Supongamos que el campo vectorial describe el campo de velocidad de un flujo de fluido (como un gran tanque de líquido o gas) y una pequeña bola está ubicada dentro del fluido o gas (el centro de la bola está fijo en un punto determinado). Si la bola tiene una superficie rugosa, el fluido que pasa por ella la hará girar. El eje de rotación (orientado según la regla de la mano derecha) apunta en la dirección del rizo del campo en el centro de la pelota, y la velocidad angular de la rotación es la mitad de la magnitud del rizo en este punto.

El rotacional del vector en cualquier punto viene dado por la rotación de un área infinitesimal en el plano xy (para el componente del eje z del rotacional), Plano zx (para el componente del eje y del rizo) y plano yz (para el eje x componente del vector rotacional). Esto se puede ver claramente en los siguientes ejemplos.

Uso

En la práctica, las dos definiciones sin coordenadas descritas anteriormente rara vez se usan porque, en prácticamente todos los casos, el operador rotacional se puede aplicar usando algún conjunto de coordenadas curvilíneas, para las cuales se han derivado representaciones más simples.

La notación ∇ × F tiene su origen en las similitudes con el producto vectorial tridimensional, y es útil como mnemónico en cartesiano. coordenadas si ∇ se toma como operador diferencial vectorial del. Tal notación que involucra operadores es común en física y álgebra.

Expandido en coordenadas cartesianas tridimensionales (ver Del en coordenadas cilíndricas y esféricas para representaciones de coordenadas esféricas y cilíndricas),∇ × F es, para F compuesto por [F_x, F_y, F_z] (donde los subíndices indican el componentes del vector, no derivadas parciales):

${displaystyle nabla times mathbf {F} ={begin{vmatrix}{boldsymbol {hat {fnMit}}} {fnMit} {fnMit}} {fnMit}} {fncipal} {fnuncio {fnMit}}} {fnMicroc} {fnMicroc} {fnMicroc}}}}}}} {fnMicroc} {f}}}}}}}}}}}}}}}}}}}} {m}}}}}}}} {m}}} {m}}}}}} {m}}} {m}}}}}}}}}}}}}}}}}}}}}}}}} {m}}} {m}}} {m}}} {m}}}} {m}}} {fnun}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}} { {partial }{partial }{dfrac {partial }\[10pt]F_{x} {c} {c} {c} {c} {c}cH}}fn}}} {f}}} {f}}}} {f}}}} {f}}f}}}}}}}}}}}}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}} {f}}} {f}}}} {f}}}}}}}}}}}}}}}}} {f}}}} {f}}}}}}} {f}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

donde i, j y k son los vectores unitarios para x-, y-, y z-ejes, respectivamente. Esto se expande de la siguiente manera:

${displaystyle nabla times mathbf {F} =left F_{z}{partial Y... ¿Qué? F_{x}{partial {fnMicroc {fnMicrosoft} ¿Qué? F_{y}{partial {fnMicroc {fnK} {fnMicrosoft Sans Serif} {fnK}}}={begin{bmatrix}{frac} {fnMicroc}} {fnMicroc} {fncip}}}}} {fncipi}} {fnMicroc} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}} {fnMicrosoft}}} {fnMicrosoft}}}}} {fnMicrosoft}}} {f}}}}} {fnMicrosoft}}}}}}}}}} { Y... {fnMicrosoft Sans Serif} ¿Qué? z}-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}} {fnMicrosoft}}} {fnMicrosoft}}}}} {fnMicrosoft}}} {f}}}}} {fnMicrosoft}}}}}}}}}} { ################################################################################################################################################################################################################################################################ {fnMicrosoft Sans Serif} F_{y}{partial {fnMicroc {fnK} {fnK}} {fnK}}} {f}}} {f}}} {fn}}}}} {f}}} {fn}}}}}} {f}}}}}}} {f}}}}}}}}}}} {f} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f}}}}}f}f}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}f}}}}f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Aunque se expresa en términos de coordenadas, el resultado es invariable bajo las rotaciones adecuadas de los ejes de coordenadas, pero el resultado se invierte bajo la reflexión.

En un sistema de coordenadas general, el rotacional viene dado por

${displaystyle (nabla times mathbf {F}{k}={frac Varepsilon ^{kell m}nabla ¿Qué?$

Donde ε denota el tensor Levi-Civita, Silencio el derivado covariante, ${displaystyle g}$ es el determinante del tensor métrico y la convención de sumación de Einstein implica que los índices repetidos se resumen. Debido a la simetría de los símbolos Christoffel que participan en el derivado covariante, esta expresión se reduce al derivado parcial:

${displaystyle (nabla times mathbf {F}={frac {1}{sqrt {g}}mathbf Varepsilon ^{kell m}partial ¿Qué?$

donde R_k son los vectores base locales. De manera equivalente, utilizando la derivada exterior, el rotacional se puede expresar como:

${displaystyle nabla times mathbf {F} =left {big (}{mathrm {d} - Sí.$

Aquí ♭ y ♯ son los isomorfismos musicales, y ★ es el operador estrella de Hodge. Esta fórmula muestra cómo calcular el rotacional de F en cualquier sistema de coordenadas y cómo extender el rotacional a cualquier variedad riemanniana tridimensional orientada. Dado que esto depende de la elección de la orientación, rotacional es una operación quiral. En otras palabras, si se invierte la orientación, también se invierte la dirección del rizo.

Ejemplos

Vector field F(x,y)=[y,-x] (izquierda) y su rizo (derecha).

Ejemplo 1

El campo vectorial

${displaystyle mathbf {F} (x,y,z)=y{boldsymbol {fnh}-x{boldsymbol {fnK}}}$

se puede descomponer como

${displaystyle F_{x}=y,F_{y}=-x,F_{z}=0.}$

Después de una inspección visual, el campo puede describirse como "giratorio". Si los vectores del campo representaran una fuerza lineal que actúa sobre los objetos presentes en ese punto, y se colocara un objeto dentro del campo, el objeto comenzaría a girar en el sentido de las agujas del reloj sobre sí mismo. Esto es cierto independientemente de dónde se coloque el objeto.

Calcular el rizo:

${displaystyle nabla times mathbf {F} =0{boldsymbol {hat {imath}}}+0{boldsymbol {hat {jmath}}}}+left({frac {partial }{partial x}(-x)-{frac {partial } {partial y}}}yderecha) {boldsymboldsymbol] {k}}=-2{boldsymbol {fnK}}}$

El campo vectorial resultante que describe el rotacional estaría apuntando en todos los puntos en la dirección z negativa. Los resultados de esta ecuación se alinean con lo que podría haberse predicho usando la regla de la mano derecha usando un sistema de coordenadas de mano derecha. Al ser un campo vectorial uniforme, el objeto descrito anteriormente tendría la misma intensidad de rotación independientemente de dónde se colocara.

Vector field F(x,y)=[0,−x²] (izquierda) y su rizo (derecha).

Ejemplo 2

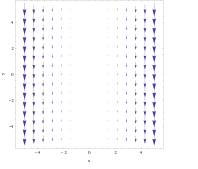
Para el campo vectorial

${displaystyle mathbf {F} (x,y,z)=-x^{2}{boldsymbol {fnK}}}$

el rizo no es tan obvio en el gráfico. Sin embargo, tomando el objeto del ejemplo anterior y colocándolo en cualquier lugar de la línea x = 3, la fuerza ejercida en el lado derecho sería ligeramente mayor que la fuerza ejercida sobre la izquierda, lo que hace que gire en el sentido de las agujas del reloj. Usando la regla de la mano derecha, se puede predecir que el rizo resultante será recto en la dirección negativa z. Inversamente, si se coloca en x = −3, el objeto rotaría en sentido antihorario y la regla de la mano derecha daría como resultado un z.

Calcular el rizo:

${displaystyle {nabla }times mathbf {F} =0{boldsymbol {hat {imath}}+0{boldsymbol {fnMith {fnh} {fnMicrosoft Sans Serif}left(-x^{2}right){boldsymbol {fnK}=-2x{boldsymbol {fnK}}}$

El rizo apunta en la dirección negativa z cuando x es positivo y viceversa. En este campo, la intensidad de rotación sería mayor a medida que el objeto se aleja del plano x = 0.

Ejemplos descriptivos

• En un campo vectorial que describe las velocidades lineales de cada parte de un disco giratorio, el rizo tiene el mismo valor en todos los puntos, y este valor resulta ser exactamente dos veces la velocidad angular vectorial del disco (orientada como de costumbre por la regla de la mano derecha). Más generalmente, para cualquier masa que fluye, el campo vectorial de velocidad lineal en cada punto del flujo de masa tiene un rizo (la vorticidad del flujo en ese punto) igual a exactamente dos veces el local Velocidad angular vectorial de la masa sobre el punto.
• Para cualquier objeto sólido sujeto a una fuerza física externa (como la gravedad o la fuerza electromagnética), se puede considerar el campo vectorial que representa las contribuciones de fuerza-por-unidad-volumen infinitesimal que actúan en cada uno de los puntos del objeto. Este campo de fuerza puede crear una red torque en el objeto sobre su centro de masa, y este par resulta ser directamente proporcional y vectorialmente paralelo a la integral (valorada por el actor) curl del campo de fuerza sobre todo el volumen.
• De las cuatro ecuaciones de Maxwell, dos —la ley de Faraday y la ley de Ampère— pueden expresarse compactamente usando curl. La ley de Faraday establece que el rizo de un campo eléctrico es igual al contrario de la velocidad de cambio del campo magnético, mientras que la ley de Ampère relaciona el rizo del campo magnético con la corriente y el tiempo de cambio del campo eléctrico.

Identidades

En coordenadas curvilíneas generales (no solo en coordenadas cartesianas), el rotacional de un producto vectorial de campos vectoriales v y F se puede demostrar que es

${displaystyle nabla times left(mathbf {vtimes F} right)={Big (}left(mathbf {nabla cdot F} right)+mathbf {Fcdot nabla } {Big)}mathbf {v} -{Big (}left(mathbf {nabla cdot v} right)+mathbf {vcdot nabla } {Big)}mathbf {F} .}$

Intercambiando el campo vectorial v y el operador ∇, llegamos al producto cruz de un campo vectorial con rotacional de un campo vectorial:

${displaystyle mathbf {vtimes } left(mathbf {nabla times F} right)=nabla _{mathbf {F}left(mathbf {vcdot F}right)-left(mathbf {vcdotnablat}bright)$

donde ∇_F es la notación de subíndice de Feynman, que considera solo la variación debida al campo vectorial F (es decir, en este caso, v se trata como una constante en el espacio).

Otro ejemplo es el rizo de un rizo de un campo vectorial. Se puede demostrar que en coordenadas generales

${displaystyle nabla times left(mathbf {nabla times F} right)=mathbf {nabla } (mathbf {nabla cdot F})-nabla ^{2}mathbf {F}}$

y esta identidad define el vector laplaciano de F, simbolizado como ∇²F.

El rotacional del gradiente de cualquier campo escalar φ es siempre el campo del vector cero

${displaystyle nabla times (nabla varphi)={boldsymbol {0}}$

que se deriva de la antisimetría en la definición del rotacional y la simetría de las segundas derivadas.

Si φ es una función con valores escalares y F es un campo vectorial, entonces

${displaystyle nabla times (varphi mathbf {F})=nabla varphi times mathbf {F} +varphi nabla times mathbf {F}$

Generalizaciones

Las operaciones de cálculo vectorial de grad, curl y div se generalizan más fácilmente en el contexto de formas diferenciales, que implica una serie de pasos. En resumen, corresponden a los derivados de 0-formas, 1-formas y 2-formas, respectivamente. La interpretación geométrica del curl como rotación corresponde a la identificación de bivectores (2-vectores) en 3 dimensiones con el álgebra especial de Lie ortogonal ${displaystyle {s} {fnK}}$3) de rotaciones infinitesimal (en coordenadas, simétricas 3 × 3 matrices), mientras que representa rotaciones por vectores corresponde a identificar 1-vectores (equivalentemente, 2-vectores) y ${displaystyle {s} {fnK}}$3), todos estos son espacios tridimensionales.

Formas diferenciales

En 3 dimensiones, una forma 0 diferencial es simplemente una función f(x, y, z); una forma diferencial 1 es la siguiente expresión, donde los coeficientes son funciones:

${displaystyle a_{1},dx+a_{2},dy+a_{3},dz;}$

una forma diferencial de 2 es la suma formal, de nuevo con coeficientes de función:

${displaystyle a_{12},dxwedge dy+a_{13},dxwedge dz+a_{23},dywedge dz;}$

y una forma diferencial de 3 se define por un solo término con una función como coeficiente:

${displaystyle a_{123},dxwedge dywedge dz.}$

(Aquí los a-coeficientes son funciones reales de tres variables; los "productos cuña", por ejemplo, dx ∧ dy, puede interpretarse como algún tipo de elementos de área orientada, dx ∧ dy = −dy ∧ dx, etc.)

La derivada exterior de una forma k en R ³ se define como la forma (k + 1) de arriba y en Rⁿ si, por ejemplo,

${displaystyle omega ^{(k)}=sum _{scriptstyle {i_{1} seleccioni_{2} scriptstyle {i_{1}ldotsn}a_{i_{1},ldotsi_{k},dx_{i_{1}}wedge cdots wedge dx_{i_{k}}}}}$

entonces la derivada exterior d conduce a

${displaystyle domega ^{(k)}=sum _{scriptstyle {j=1} atop scriptstyle {fn} {fn} {fn} {fn}fn} {fn}fn} {fn}} {fn}fn}} {fn}} {fnfnfnK}}}} {fnfnK}}}} {fnKfnK}}}}}}}}}} {f}}}}}}}}}}}}}}}}}\\\\p9}}}}}}}}}\\cdot\\cdotcdotcdot}}}}}}}}}}}}}}}}}} {cdot}}} {cdot}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\cdot}}}}}}}}}} {cdot}}}}} ################################################################################################################################################################################################################################################################ dx_{i_{1}wedge cdots wedge dx_{i_{k}.}$

La derivada exterior de una forma 1 es, por lo tanto, una forma 2, y la de una forma 2 es una forma 3. Por otro lado, debido a la intercambiabilidad de los derivados mixtos, p. porque

${displaystyle {frac {partial ^{2}{partial x,partial y}}={frac {partial ^{2}}{partial y,partial x}}}} {fnMicroc {c}}} {cccccH00}}}}}}}$

la doble aplicación de la derivada exterior conduce a 0.

Por lo tanto, denotando el espacio de k-formas por Ω^k(R³) y la derivada exterior por d< /span> se obtiene una secuencia:

${displaystyle 0,{overset {d}{longrightarrow };Omega ^{0}left(mathbb {R} ^{3}right),{overset {d}{longrightarrow };Omega ^{1}left(mathbb {R} ^{3}right),{overset {d} {longrightarrow };Omega ^{2}left(mathbb {R} ^{3}right),{overset {d}{}};Omega ^{3}left(mathbb {R} ^{3}right),{overset {d}{longrightarrow },0}$

Aquí Ω^k(Rⁿ⁾ es el espacio de secciones del álgebra exterior Λ^k(R< sup>n) paquete vectorial sobre Rⁿ, cuya dimensión es la coeficiente binomial ( ⁿ
_k< /span>); tenga en cuenta que Ω^k(R³) = 0 para k > 3 o k < 0. Escribiendo solo dimensiones, se obtiene una fila del triángulo de Pascal:

0 → 1 → 3 → 3 → 1 → 0;

las fibras unidimensionales corresponden a campos escalares y las fibras tridimensionales a campos vectoriales, como se describe a continuación. Modulo identificaciones adecuadas, las tres ocurrencias no triviales de la derivada exterior corresponden a grad, curl y div.

Las formas diferenciales y el diferencial se pueden definir en cualquier espacio euclidiano, o incluso en cualquier variedad, sin ninguna noción de métrica de Riemann. En una variedad Riemanniana, o más generalmente variedad pseudo-Riemanniana, las formas k pueden identificarse con campos de vectores k (k son k-campos covectoriales, y una métrica pseudo-riemanniana da un isomorfismo entre vectores y covectores), y en un espacio vectorial orientado con una forma no degenerada (un isomorfismo entre vectores y covectores), existe un isomorfismo entre k< /i>-vectores y (n − k)-vectores; en particular en (el espacio tangente de) una variedad pseudo-Riemanniana orientada. Por lo tanto, en una variedad pseudo-Riemanniana orientada, uno puede intercambiar formas k, k-campos vectoriales, (n − k)-formas y (n − k)-campos vectoriales; esto se conoce como dualidad de Hodge. Concretamente, en R³ esto viene dado por:

• 1-formas y campos 1-vector: el 1-form a_x dx + a_Sí. dy + a_z dz corresponde al campo vectorial ()a_x, a_Sí., a_z).
• 1-formas y 2-formas: una reemplaza dx por la cantidad dual dy ∧ dz (es decir, omit dx), y también, cuidando de la orientación: dy corresponde a dz ∧ dx =dx ∧ dz, y dz corresponde a dx ∧ dy. Así la forma a_x dx + a_Sí. dy + a_z dz corresponde a la "forma dual" a_z dx ∧ dy + a_Sí. dz ∧ dx + a_x dy ∧ dz.

Por lo tanto, identificando formas 0 y formas 3 con campos escalares, y formas 1 y formas 2 con campos vectoriales:

• grad toma un campo de escalar (0-form) a un campo vectorial (1-form);
• curl lleva un campo vectorial (1-form) a un campo pseudovector (2-form);
• div toma un campo pseudovector (2-form) a un campo pseudoescalar (3-form)

Por otro lado, el hecho de que d²< /span> = 0 corresponde a las identidades

${displaystyle nabla times (nabla f)=0}$

para cualquier campo escalar f, y

${displaystyle nabla cdot (nabla times mathbf {v}=0}$

para cualquier campo vectorial v.

Grad y div se generalizan a todas las variedades pseudo-Riemannianas orientadas, con la misma interpretación geométrica, porque los espacios de formas 0 y n- las formas en cada punto son siempre unidimensionales y se pueden identificar con campos escalares, mientras que los espacios de 1-formas y (n − 1)- los formularios son siempre n-dimensionales y se pueden identificar con campos vectoriales.

Curl no generaliza de esta manera a 4 o más dimensiones (o hasta 2 o menos dimensiones); en 4 dimensiones las dimensiones son

0 → 1 → 4 → 6 → 4 → 1 → 0;

entonces el rotacional de un campo de 1 vector (fibra cuadridimensional) es un campo de 2 vectores, que en cada punto pertenece al espacio vectorial de 6 dimensiones, por lo que uno tiene

${displaystyle omega ^{(2)}=sum ################################################################################################################################################################################################################################################################ Dx_{k},}$

que produce una suma de seis términos independientes y no se puede identificar con un campo de 1 vector. Tampoco se puede pasar significativamente de un campo de 1 vector a un campo de 2 vectores a un campo de 3 vectores (4 → 6 → 4), ya que tomar el diferencial dos veces arroja cero ( d² = 0). Por lo tanto, no existe una función rotacional de campos vectoriales a campos vectoriales en otras dimensiones que surjan de esta manera.

Sin embargo, se puede definir un rizo de un campo vectorial como un campo de 2 vectores en general, como se describe a continuación.

Rizar geométricamente

2-vectores corresponden a la potencia exterior ▪²V; en presencia de un producto interior, en las coordenadas estas son las matrices simétricas de cerda, que se consideran geométricamente como la ortogonal especial Lie algebra ${displaystyle {s} {fnK}}$()V) de rotaciones infinitesimal. Esto tiene ()ⁿ
₂) = 1/2n()n −1) dimensiones, y permite interpretar el diferencial de un campo de 1-vector como sus rotaciones infinitesimal. Sólo en 3 dimensiones (o trivialmente en 0 dimensiones) n = 1/2n()n −1), que es el caso más elegante y común. En 2 dimensiones el borde de un campo vectorial no es un campo vectorial sino una función, ya que las rotaciones 2-dimensionales son dadas por un ángulo (un escalar – se requiere una orientación para elegir si se cuenta las rotaciones en sentido de reloj o en sentido contrario como positivo); esto no es el div, pero es más bien perpendicular a él. En 3 dimensiones el rizo de un campo vectorial es un campo vectorial como es familiar (en 1 y 0 dimensiones el rizo de un campo vectorial es 0, porque no hay 2-vectores no-triviales), mientras que en 4 dimensiones el rizo de un campo vectorial es, geométricamente, en cada punto un elemento del álgebra de Lie 6-dimensional ${\displaystyle {\sh} {fnMicrosoft}} {fnMicrosoft}}} {fnK}}}}$.

El rotacional de un campo vectorial tridimensional que solo depende de 2 coordenadas (por ejemplo, x y < i>y) es simplemente un campo vectorial vertical (en la dirección z) cuya magnitud es el rotacional del Campo vectorial bidimensional, como en los ejemplos de esta página.

Se ha utilizado la consideración del rotacional como un campo de 2 vectores (un tensor de 2 antisimétrico) para generalizar el cálculo vectorial y la física asociada a dimensiones más altas.

Inversa

En el caso de que la divergencia de un campo vectorial V sea cero, un campo vectorial W existe tal que V = curl(W). Esta es la razón por la cual el campo magnético, caracterizado por la divergencia cero, puede expresarse como el rotacional de un vector potencial magnético.

Si W es un campo vectorial con curl(W) = < b>V, luego agregue cualquier campo de vector de gradiente grad(f) a W dará como resultado otro campo vectorial W + grad(f) tal que curl(W + grad(f)) = V también. Esto se puede resumir diciendo que el rotacional inverso de un campo vectorial tridimensional se puede obtener hasta un campo irrotacional desconocido con la ley de Biot-Savart.