Retrato de fase


En matemáticas, un retrato de fase es una representación geométrica de las órbitas de un sistema dinámico en el plano de fase. Cada conjunto de condiciones iniciales está representado por un punto o curva diferente.
Los retratos de fase son una herramienta invaluable para estudiar sistemas dinámicos. Consisten en un gráfico de trayectorias típicas en el espacio de fases. Esto revela información como si un atractor, un repelente o un ciclo límite está presente para el valor del parámetro elegido. El concepto de equivalencia topológica es importante para clasificar el comportamiento de los sistemas al especificar cuándo dos retratos de fase diferentes representan el mismo comportamiento dinámico cualitativo. Un atractor es un punto estable que también se denomina "sumidero". El repelente se considera un punto inestable, que también se conoce como "fuente".
Un gráfico de retrato de fase de un sistema dinámico representa las trayectorias del sistema (con flechas) y los estados estables (con puntos) e inestables (con círculos) en un espacio de fases. Los ejes son las variables de estado.
Ejemplos
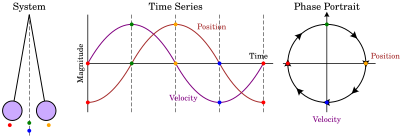
- Péndulo simple, ver imagen (derecha).
- Un simple oscilador armónico donde el retrato de fase se compone de elipses centrados en el origen, que es un punto fijo.
- Movimiento armónico dañado, vea la animación (derecha).
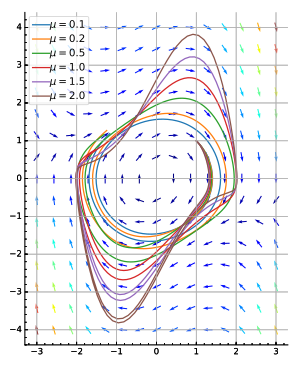
- Van der Pol oscillator ver imagen (abajo derecho).
Visualización del comportamiento de las ecuaciones diferenciales ordinarias
Un retrato de fase representa el comportamiento direccional de un sistema de ecuaciones diferenciales ordinarias (EDO). El retrato de fase puede indicar la estabilidad del sistema.
| Inestable | La mayor parte de las soluciones del sistema tienden hacia ∞ con el tiempo |
| Asintotically stable | Todas las soluciones del sistema tienden a 0 con el tiempo |
| Neutralmente estable | Ninguna de las soluciones del sistema tienden hacia ∞ con el tiempo, pero la mayoría de las soluciones no tienden hacia 0 o |
El comportamiento del retrato de fase de un sistema de EDO se puede determinar mediante los valores propios o la traza y el determinante (traza = λ1 + λ2, determinante = λ1 x λ2) del sistema.
| Eigenvalue, Trace, Determinant | Forma de retrato de fase |
|---|---|
| λ1 " λ2 son reales y de signo opuesto;
Determinante 0 | Silla (inestable) |
| λ1 " λ2 son reales y del mismo signo, y λ1 ■2;
0 0 determinado determinador2 4) | Nodo (establecido si traza < 0, inestable si traza 0) |
| λ1 " λ2 tienen un componente real e imaginario;
(trace2 4) Determinante | Espiral (estable si traza ) 0, inestable si traza 0) |
Véase también
- Espacio de fase
- Plano de fase
Referencias
- ^ a b c d Haynes Miller y Arthur Mattuck. 18.03 Ecuaciones diferenciales. Primavera 2010. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. Licencia: Creative Commons BY-NC-SA. (Notas complementarias 26 de Haynes Miller: https://ocw.mit.edu/courses/18-03-differential-equations-spring-2010/resources/mit18_03s10_chapter_26/)
- Jordania, D. W.; Smith, P. (2007). Ecuaciones diferenciales no lineales (cuarta edición). Oxford University Press. ISBN 978-0-19-920824-1. Capítulo 1.
- Steven Strogatz (2001). Dinámica y Caos no lineales: Con aplicaciones para Física, Biología, Química e Ingeniería. ISBN 9780738204536.
Enlaces externos
- Retratos de fase lineal, un matemático MIT.

