Respuesta frecuente

En procesamiento de señales y electrónica, la respuesta de frecuencia de un sistema es la medida cuantitativa de la magnitud y la fase de la salida en función de la frecuencia de entrada. La respuesta de frecuencia se usa ampliamente en el diseño y análisis de sistemas, como sistemas de audio y control, donde simplifican el análisis matemático al convertir las ecuaciones diferenciales gobernantes en ecuaciones algebraicas. En un sistema de audio, se puede usar para minimizar la distorsión audible mediante el diseño de componentes (como micrófonos, amplificadores y altavoces) para que la respuesta general sea lo más plana (uniforme) posible en todo el ancho de banda del sistema. En los sistemas de control, como el control de crucero de un vehículo, se puede utilizar para evaluar la estabilidad del sistema, a menudo mediante el uso de diagramas de Bode. Se pueden diseñar sistemas con una respuesta de frecuencia específica utilizando filtros analógicos y digitales.

La respuesta de frecuencia caracteriza los sistemas en el dominio de frecuencia, así como la respuesta de impulso caracteriza los sistemas en el dominio del tiempo. En sistemas lineales (o como aproximación a un sistema real descuidando las propiedades no lineales de segundo orden), bien la respuesta describe completamente el sistema y por lo tanto tiene una correspondencia única: la respuesta de frecuencia es la transformación Fourier de la respuesta del impulso. La respuesta de frecuencia permite un análisis más simple de sistemas cascadados como amplificadores multietapa, ya que la respuesta del sistema general se puede encontrar mediante la multiplicación de las respuestas de frecuencia de las etapas individuales (en contraposición a la convolución de la respuesta de impulso en el dominio del tiempo). La respuesta de frecuencia está estrechamente relacionada con la función de transferencia en sistemas lineales, que es la transformación de Laplace de la respuesta del impulso. Son equivalentes cuando la parte real σ σ {displaystyle sigma } la variable compleja de la función de transferencia s=σ σ +j⋅ ⋅ {displaystyle s=sigma +jomega } es cero.

Medición y trazado

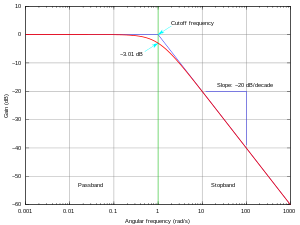
La medición de la respuesta de frecuencia generalmente implica excitar el sistema con una señal de entrada y medir la señal de salida resultante, calcular los espectros de frecuencia de las dos señales (por ejemplo, usar la transformada rápida de Fourier para señales discretas) y comparar los espectros con aislar el efecto del sistema. En sistemas lineales, el rango de frecuencia de la señal de entrada debe cubrir el rango de frecuencia de interés.

Se pueden usar varios métodos que utilizan diferentes señales de entrada para medir la respuesta de frecuencia de un sistema, incluidos:

• Aplicando la amplitud constante de los sinusoides paso a través de una gama de frecuencias y comparando la amplitud y el cambio de fase de la salida en relación con la entrada. El barrido de frecuencia debe ser lo suficientemente lento para que el sistema alcance su estado estable en cada punto de interés
• Aplicar una señal de impulso y tomar la transformación Fourier de la respuesta del sistema
• Aplicando una señal de ruido blanco estacionario de amplio sentido durante un largo período de tiempo y tomando la transformación Fourier de la respuesta del sistema. Con este método, se debe utilizar la densidad transversal (en lugar de la densidad espectral de potencia) si se requiere información de fase

La respuesta de frecuencia se caracteriza por la magnitud, normalmente en decibelios (dB) o como una amplitud genérica de la variable dependiente, y la fase, en radianes o grados, medido contra la frecuencia, en radianes/s, Hertz (Hz) o como una fracción de la frecuencia de muestreo.

Hay tres formas comunes de trazar medidas de respuesta:

• Parcelas de bode graph magnitud y fase contra frecuencia en dos parcelas rectangulares
• Parcelas Nyquist graph magnitud y fase paramétricamente contra frecuencia en forma polar
• Nichols trama gráfica magnitud y fase paramétricamente contra frecuencia en forma rectangular

Para el diseño de sistemas de control, se puede utilizar cualquiera de los tres tipos de diagramas para inferir la estabilidad de bucle cerrado y los márgenes de estabilidad a partir de la respuesta de frecuencia de bucle abierto. En muchas aplicaciones en el dominio de la frecuencia, la respuesta de fase es relativamente poco importante y la respuesta de magnitud del diagrama de Bode puede ser todo lo que se requiere. En los sistemas digitales (como los filtros digitales), la respuesta de frecuencia a menudo contiene un lóbulo principal con múltiples lóbulos laterales periódicos, debido a la fuga espectral causada por procesos digitales como el muestreo y la creación de ventanas.

Respuesta de frecuencia no lineal

Si el sistema bajo investigación no es lineal, el análisis de dominio de frecuencia lineal no revelará todas las características no lineales. Para superar estas limitaciones, se han definido funciones de respuesta de frecuencia generalizadas y funciones de respuesta de frecuencia de salida no lineales para analizar los efectos dinámicos no lineales. Los métodos de respuesta de frecuencia no lineal pueden revelar efectos tales como resonancia, intermodulación y transferencia de energía.

Aplicaciones

En el rango audible, la respuesta de frecuencia generalmente se refiere a amplificadores electrónicos, micrófonos y altavoces. La respuesta de frecuencia del espectro de radio puede referirse a mediciones de cable coaxial, cable de par trenzado, equipos de conmutación de video, dispositivos de comunicaciones inalámbricas y sistemas de antena. Las mediciones de respuesta de frecuencia infrasónica incluyen terremotos y electroencefalografía (ondas cerebrales).

Las curvas de respuesta de frecuencia se utilizan a menudo para indicar la precisión de los componentes o sistemas electrónicos. Cuando un sistema o componente reproduce todas las señales de entrada deseadas sin énfasis ni atenuación de una banda de frecuencia particular, se dice que el sistema o componente es "plano" o que tiene una curva de respuesta de frecuencia plana. En otro caso, podemos usar una forma 3D de superficie de respuesta de frecuencia.

Los requisitos de respuesta de frecuencia difieren según la aplicación. En audio de alta fidelidad, un amplificador requiere una respuesta de frecuencia plana de al menos 20 - 20 000 Hz, con una tolerancia tan estrecha como ±0,1 dB en las frecuencias de rango medio alrededor de 1000 Hz; sin embargo, en telefonía, una respuesta de frecuencia de 400 a 4000 Hz, con una tolerancia de ±1 dB es suficiente para la inteligibilidad del habla.

Una vez que se ha medido una respuesta de frecuencia (por ejemplo, como una respuesta de impulso), siempre que el sistema sea lineal e invariable en el tiempo, su característica puede aproximarse con precisión arbitraria mediante un filtro digital. De manera similar, si se demuestra que un sistema tiene una respuesta de frecuencia deficiente, se puede aplicar un filtro digital o analógico a las señales antes de su reproducción para compensar estas deficiencias.

La forma de una curva de respuesta de frecuencia es muy importante para la protección antiinterferencias de radares, comunicaciones y otros sistemas.

El análisis de respuesta de frecuencia también se puede aplicar a dominios biológicos, como la detección de hormesis en comportamientos repetidos con dinámicas de procesos oponentes, o en la optimización de regímenes de tratamiento farmacológico.