Resonancia orbital

En la mecánica celeste, la resonancia orbital se produce cuando los cuerpos en órbita ejercen una influencia gravitacional regular y periódica entre sí, generalmente porque sus períodos orbitales están relacionados por una proporción de números enteros pequeños. Más comúnmente, esta relación se encuentra entre un par de objetos (resonancia binaria). El principio físico detrás de la resonancia orbital es similar en concepto a empujar a un niño en un columpio, donde la órbita y el columpio tienen una frecuencia natural, y el cuerpo que realiza el 'empuje' actuará en repetición periódica para tener un efecto acumulativo en el movimiento. Las resonancias orbitales mejoran en gran medida la influencia gravitacional mutua de los cuerpos (es decir, su capacidad para alterar o restringir las órbitas de los demás). En la mayoría de los casos, esto da como resultado una interacción inestable, en la que los cuerpos intercambian impulso y cambian de órbita hasta que la resonancia ya no existe. En algunas circunstancias, un sistema resonante puede autocorregirse y, por lo tanto, ser estable. Algunos ejemplos son la resonancia 1:2:4 de las lunas de Júpiter, Ganímedes, Europa e Io, y la resonancia 2:3 entre Plutón y Neptuno. Las resonancias inestables con las lunas internas de Saturno dan lugar a espacios en los anillos de Saturno. El caso especial de resonancia 1:1 entre cuerpos con radios orbitales similares hace que los grandes cuerpos del sistema solar expulsen a la mayoría de los demás cuerpos que comparten sus órbitas; esto es parte del proceso mucho más extenso de limpiar el vecindario, un efecto que se usa en la definición actual de un planeta.
Una relación de resonancia binaria en este artículo debe interpretarse como la relación del número de órbitas completadas en el mismo intervalo de tiempo, en lugar de como la relación de períodos orbitales, que sería la razón inversa. Por lo tanto, la proporción de 2:3 anterior significa que Plutón completa dos órbitas en el tiempo que le toma a Neptuno completar tres. En el caso de relaciones de resonancia entre tres o más cuerpos, se puede usar cualquier tipo de relación (donde las secuencias de relación de entero entero más pequeñas no son necesariamente inversiones entre sí), y se especificará el tipo de relación.
Historia
Desde el descubrimiento de la ley de gravitación universal de Newton en el siglo XVII, la estabilidad del Sistema Solar ha preocupado a muchos matemáticos, empezando por Pierre-Simon Laplace. Las órbitas estables que surgen en una aproximación de dos cuerpos ignoran la influencia de otros cuerpos. El efecto de estas interacciones añadidas en la estabilidad del Sistema Solar es muy pequeño, pero al principio no se sabía si se sumarían durante períodos más largos para cambiar significativamente los parámetros orbitales y dar lugar a una configuración completamente diferente, o si alguna otra los efectos estabilizadores podrían mantener la configuración de las órbitas de los planetas.
Fue Laplace quien encontró las primeras respuestas que explican las órbitas vinculadas de las lunas galileanas (ver más abajo). Antes de Newton, también se consideraron razones y proporciones en los movimientos orbitales, en lo que se llamó "la música de las esferas", o musica universalis.
El artículo sobre interacciones resonantes describe la resonancia en el entorno moderno general. Un resultado principal del estudio de los sistemas dinámicos es el descubrimiento y la descripción de un modelo muy simplificado de bloqueo de modo; este es un oscilador que recibe patadas periódicas a través de un acoplamiento débil a algún motor impulsor. El análogo aquí sería que un cuerpo más masivo proporciona una patada gravitatoria periódica a un cuerpo más pequeño, a medida que pasa. Las regiones de bloqueo de modo se denominan lenguas de Arnold.
Tipos de resonancia
En general, una resonancia orbital puede
- involucrar una o cualquier combinación de los parámetros de órbita (por ejemplo, excentricidad versus eje semimajor, o excentricidad versus inclinación).
- actuar en cualquier escala de tiempo de corto plazo, acorde con los períodos de órbita, a secular, medido en 104 a 106 años.
- conducir a una estabilización a largo plazo de las órbitas o ser la causa de su desestabilización.
Una resonancia orbital de movimiento medio ocurre cuando dos cuerpos tienen períodos de revolución que son una razón entera simple entre sí. Dependiendo de los detalles, esto puede estabilizar o desestabilizar la órbita. La estabilización puede ocurrir cuando los dos cuerpos se mueven de manera tan sincronizada que nunca se acercan demasiado. Por ejemplo:
- Las órbitas de Plutón y los plutinos son estables, a pesar de cruzar el Neptuno mucho más grande, porque están en una resonancia 2:3 con él. La resonancia asegura que, cuando se acercan a la perihelión y a la órbita de Neptuno, Neptuno está constantemente distante (promedio de una cuarta parte de su órbita). Otros (mucho más numerosos) cuerpos de cruce de neptuno que no estaban en resonancia fueron expulsados de esa región por fuertes perturbaciones debido a Neptuno. También hay grupos más pequeños pero significativos de objetos resonantes trans-neptunianos que ocupan el 1:1 (Neptuno troyanos), 3:5, 4:7, 1:2 (dostinos) y 2:5 resonancias, entre otros, con respecto a Neptuno.
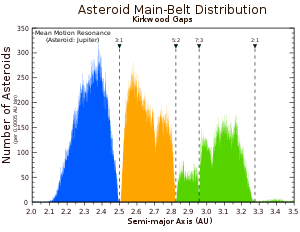
- En el cinturón de asteroides más allá de 3.5 UA del Sol, las resonancias 3:2, 4:3 y 1:1 con Júpiter son pobladas por bultos de asteroides (la familia Hilda, los pocos asteroides Thule, y los numerosos asteroides de Troya, respectivamente).
Las resonancias orbitales también pueden desestabilizar una de las órbitas. Este proceso puede aprovecharse para encontrar formas energéticamente eficientes de desorbitar naves espaciales. Para cuerpos pequeños, la desestabilización es mucho más probable. Por ejemplo:
- En el cinturón de asteroides dentro de 3,5 U del Sol, las principales resonancias de media-moción con Júpiter son lugares de deficiencias en la distribución de asteroides, las lagunas de Kirkwood (principalmente en las resonancias 4:1, 3:1, 5:2, 7:3 y 2:1). Los asteroides han sido expulsados de estos carriles casi vacíos por perturbaciones repetidas. Sin embargo, todavía hay poblaciones de asteroides presentes temporalmente en o cerca de estas resonancias. Por ejemplo, asteroides de la familia Alinda están dentro o cerca de la resonancia 3:1, con su excentricidad orbital aumentada constantemente por interacciones con Júpiter hasta que finalmente tengan un encuentro cercano con un planeta interior que los expulsa de la resonancia.
- En los anillos de Saturno, la División Cassini es una brecha entre el anillo B interior y el anillo A exterior que ha sido aclarado por una resonancia de 2:1 con la luna Mimas. (Más específicamente, el sitio de la resonancia es el Huygens Gap, que limita el borde exterior del anillo B.)
- En los anillos de Saturno, las lagunas de Encke y Keeler dentro del Anillo A se limpian por 1:1 resonancias con las lunas incrustadas Pan y Daphnis, respectivamente. El borde exterior de A Ring se mantiene por una resonancia desestabilizadora 7:6 con la luna Janus.
La mayoría de los cuerpos que están en resonancia orbitan en la misma dirección; sin embargo, el asteroide retrógrado 514107 Kaʻepaokaʻawela parece estar en una resonancia estable (durante un período de al menos un millón de años) 1:−1 con Júpiter. Además, se han encontrado algunos damocloides retrógrados que se capturan temporalmente en resonancia de movimiento medio con Júpiter o Saturno. Tales interacciones orbitales son más débiles que las correspondientes interacciones entre cuerpos que orbitan en la misma dirección.
Una resonancia de Laplace es una resonancia de tres cuerpos con una relación de período orbital de 1:2:4 (equivalente a una relación de órbitas de 4:2:1). El término surgió porque Pierre-Simon Laplace descubrió que tal resonancia gobernaba los movimientos de las lunas de Júpiter, Io, Europa y Ganímedes. Ahora también se aplica a menudo a otras resonancias de 3 cuerpos con las mismas proporciones, como la que existe entre los planetas extrasolares Gliese 876 c, b y e. Las resonancias de tres cuerpos que involucran otras proporciones de enteros simples se han denominado "similares a Laplace" o "tipo Laplace".
Una resonancia de Lindblad genera ondas de densidad espiral tanto en las galaxias (donde las estrellas están sujetas a la fuerza de los propios brazos espirales) como en los anillos de Saturno (donde las partículas del anillo están sujetas a la fuerza de los propios brazos espirales). las lunas de Saturno).
Una resonancia secular ocurre cuando la precesión de dos órbitas está sincronizada (generalmente una precesión del perihelio o nodo ascendente). Un cuerpo pequeño en resonancia secular con uno mucho más grande (por ejemplo, un planeta) precesionará al mismo ritmo que el cuerpo grande. Durante mucho tiempo (un millón de años, más o menos) una resonancia secular cambiará la excentricidad y la inclinación del cuerpo pequeño.
Varios ejemplos destacados de resonancia secular involucran a Saturno. Hay una resonancia cercana entre la precesión del eje de rotación de Saturno y la del eje orbital de Neptuno (ambos tienen períodos de alrededor de 1,87 millones de años), que se ha identificado como la fuente probable de Saturno. Gran inclinación axial (26,7°). Inicialmente, Saturno probablemente tenía una inclinación más cercana a la de Júpiter (3,1°). El agotamiento gradual del cinturón de Kuiper habría disminuido la tasa de precesión de la órbita de Neptuno; eventualmente, las frecuencias coincidieron y la precesión axial de Saturno fue capturada en una resonancia de giro-órbita, lo que llevó a un aumento en la oblicuidad de Saturno. (El momento angular de la órbita de Neptuno es 104 veces mayor que la velocidad de rotación de Saturno y, por lo tanto, domina la interacción). Sin embargo, parece que la resonancia ya no existe. El análisis detallado de los datos de la nave espacial Cassini da un valor del momento de inercia de Saturno que está justo fuera del rango para que exista la resonancia, lo que significa que el eje de giro no permanece en fase con la inclinación orbital de Neptuno en el largo plazo, como aparentemente lo hizo en el pasado. Una teoría de por qué terminó la resonancia es que había otra luna alrededor de Saturno cuya órbita se desestabilizó hace unos 100 millones de años, perturbando a Saturno.
La resonancia secular del perihelio entre los asteroides y Saturno (ν6 = g − g6 ) ayuda a dar forma al cinturón de asteroides (el subíndice "6" identifica a Saturno como el sexto planeta desde el Sol). Los asteroides que se acercan a él tienen su excentricidad aumentada lentamente hasta que se convierten en cruces de Marte, momento en el que generalmente son expulsados del cinturón de asteroides por un paso cercano a Marte. Esta resonancia forma el interior y el "lateral" límites del cinturón de asteroides alrededor de 2 UA, y con inclinaciones de unos 20°.
Las simulaciones numéricas han sugerido que la eventual formación de una resonancia secular perihelio entre Mercurio y Júpiter (g1 = g5 ) tiene el potencial de aumentar en gran medida la excentricidad de Mercurio y posiblemente desestabilizar el Sistema Solar interior dentro de varios miles de millones de años.
El Titán Ringlet dentro del Anillo C de Saturno representa otro tipo de resonancia en el que la velocidad de precesión absidal de una órbita coincide exactamente con la velocidad de revolución de otra. El extremo exterior de este anillo excéntrico siempre apunta hacia la luna principal de Saturno, Titán.
Una resonancia Kozai ocurre cuando la inclinación y la excentricidad de una órbita perturbada oscilan sincrónicamente (aumentando la excentricidad mientras disminuye la inclinación y viceversa). Esta resonancia se aplica solo a cuerpos en órbitas muy inclinadas; como consecuencia, tales órbitas tienden a ser inestables, ya que la creciente excentricidad daría como resultado pequeños pericentros, lo que generalmente conduciría a una colisión o (para lunas grandes) a la destrucción por las fuerzas de marea.
En un ejemplo de otro tipo de resonancia que implica excentricidad orbital, las excentricidades de Ganímedes y Calisto varían con un período común de 181 años, aunque con fases opuestas.
Resonancias de movimiento medio en el Sistema Solar
Solo hay unas pocas resonancias de movimiento medio conocidas (MMR) en el Sistema Solar que involucran planetas, planetas enanos o satélites más grandes (un número mucho mayor involucra asteroides, anillos planetarios, lunas y objetos más pequeños del cinturón de Kuiper, incluidos muchos posibles enanos). planetas).
- 2:3 Plutón-Neptuno (también Orcus y otros plutinos)
- 2:4 Tethys – Mimas (lunas de Saturn). No simplificado, porque se debe tener en cuenta la libración de los nodos.
- 1:2 Dione–Enceladus (Las lunas de gira)
- 3:4 Hiperión – Titán (lunas de la gira)
- 1:2:4 Ganymede–Europa–Io (lunas de Júpiter, proporción de órbitas).
Además, se cree que Haumea está en una resonancia de 7:12 con Neptuno y que Gonggong está en una resonancia de 3:10 con Neptuno.
Las proporciones de enteros simples entre períodos esconden relaciones más complejas:
- el punto de conjunción puede oscilar (librar) alrededor de un punto de equilibrio definido por la resonancia.
- dadas excentricidades no cero, los nodos o los periapsides pueden derivar (una resonancia relacionada, corto período, no precesión secular).
Como ilustración de este último, considere la conocida resonancia 2:1 de Io-Europa. Si los períodos orbitales estaban en esta relación, los movimientos medios n{displaystyle n,!} (inverso de períodos, a menudo expresados en grados por día) satisfaría lo siguiente
- nIo− − 2⋅ ⋅ nEu=0{displaystyle n_{rm [Io]}-2cdot n_{rm {Eu}=0}
Sustituyendo los datos (de Wikipedia) se obtiene −0,7395° día−1, un valor sustancialmente distinto de cero.
En realidad, la resonancia es perfecto, pero implica también la precesión de perijove (el punto más cercano a Júpiter), ⋅ ⋅ Í Í {displaystyle {dot {fnMiega }. La ecuación correcta (parte de las ecuaciones de Laplace) es:
- nIo− − 2⋅ ⋅ nEu+⋅ ⋅ Í Í Io=0{displaystyle n_{rm {Io}-2cdot n_{rm} {Eu}+{dot {omega ♪♪ {Io}=0}
En otras palabras, el movimiento medio de Io es de hecho el doble del de Europa teniendo en cuenta la precesión del perijove. Un observador sentado en el perijove (a la deriva) verá las lunas en conjunción en el mismo lugar (alargamiento). Los otros pares enumerados anteriormente satisfacen el mismo tipo de ecuación con la excepción de la resonancia de Mimas-Tethys. En este caso, la resonancia satisface la ecuación
- 4⋅ ⋅ nTe− − 2⋅ ⋅ nMi− − Ω Ω Í Í Te− − Ω Ω Í Í Mi=0{displaystyle 4cdot n_{rm {Te}-2cdot n_{rm} {Mi}-{dot ################################################################################################################################################################################################################################################################ ♪♪ {Te}-{dot ################################################################################################################################################################################################################################################################ ♪♪ {Mi}=0}
El punto de conjunción se libra alrededor del punto medio entre los nodos de las dos lunas.
Resonancia de Laplace
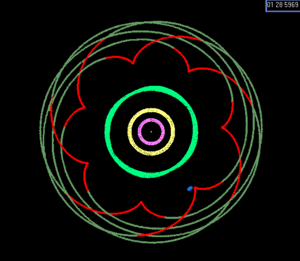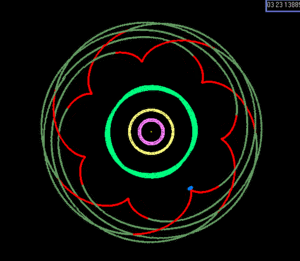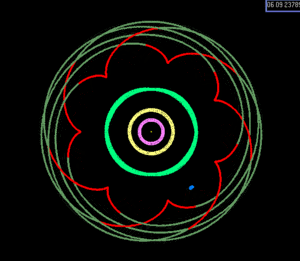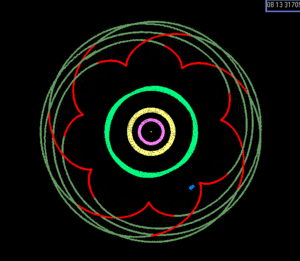
La resonancia de Laplace que involucra a Io–Europa–Ganymede incluye la siguiente relación que bloquea la fase orbital de las lunas:
- CCPR CCPR L=λ λ Io− − 3⋅ ⋅ λ λ Eu+2⋅ ⋅ λ λ Ga=180∘ ∘ {displaystyle Phi _{L}=lambda _{rm {Io}}-3cdot lambda _{rm {Eu}+2cdot lambda _{rm {}=180}{circ}}
Donde λ λ {displaystyle lambda } son longitudes medias de las lunas (el segundo signo igual ignora la libración).
Esta relación hace imposible una triple conjunción. (Una resonancia en el sistema Gliese 876, por el contrario, se asocia con una triple conjunción por órbita del planeta más exterior, ignorando la libración). El gráfico ilustra las posiciones de las lunas después de 1, 2 y 3 periodos Io. CCPR CCPR L{displaystyle ¿Qué? libra alrededor de 180° con una amplitud de 0.03°.
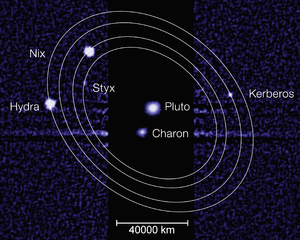
Otra "Laplace-like" la resonancia involucra a las lunas Styx, Nix e Hydra de Plutón:
- CCPR CCPR =3⋅ ⋅ λ λ S− − 5⋅ ⋅ λ λ N+2⋅ ⋅ λ λ H=180∘ ∘ {displaystyle Phi =3cdot lambda _{rm {S}-5cdot lambda ¿Por qué?
Esto refleja períodos orbitales para Styx, Nix e Hydra, respectivamente, que están cerca de una proporción de 18:22:33 (o, en términos de las resonancias cercanas con el período de Charon, 3+3/11:4:6; ver abajo); la relación respectiva de órbitas es 11:9:6. Basado en las ratios de periodos sinódicos, hay 5 conjunciones de Styx y Hydra y 3 conjunciones de Nix y Hydra para cada 2 conjunciones de Styx y Nix. Al igual que con la resonancia del satélite Galileo, se prohíben triples conjunciones. CCPR CCPR {displaystyle Phi } libra alrededor de 180° con una amplitud de al menos 10°.
Resonancias de Plutino
El planeta enano Plutón sigue una órbita atrapada en una red de resonancias con Neptuno. Las resonancias incluyen:
- Una resonancia media-moción de 2:3
- La resonancia del perihelio (libración alrededor de 90°), manteniendo el perihelio por encima de la eclíptica
- La resonancia de la longitud del perihelio en relación con la de Neptuno
Una consecuencia de estas resonancias es que se mantiene una separación de al menos 30 AU cuando Plutón cruza la órbita de Neptuno. La separación mínima entre los dos cuerpos en general es de 17 UA, mientras que la separación mínima entre Plutón y Urano es de solo 11 UA (consulte la órbita de Plutón para obtener una explicación detallada y gráficos).
El siguiente cuerpo más grande en una resonancia similar de 2:3 con Neptuno, llamado plutino, es el probable planeta enano Orcus. Orcus tiene una órbita similar en inclinación y excentricidad a la de Plutón. Sin embargo, los dos están obligados por su resonancia mutua con Neptuno a estar siempre en fases opuestas de sus órbitas; Por lo tanto, a veces se describe a Orcus como el "anti-Plutón".
Náyade: Thalassa 73:69 resonancia
La luna más interna de Neptuno, Náyade, está en una resonancia de cuarto orden de 73:69 con la siguiente luna exterior, Thalassa. A medida que orbita a Neptuno, la Náyade más inclinada pasa sucesivamente a Thalassa dos veces desde arriba y luego dos veces desde abajo, en un ciclo que se repite cada ~21,5 días terrestres. Las dos lunas están separadas por unos 3540 km cuando se cruzan. Aunque sus radios orbitales difieren en solo 1850 km, Naiad oscila ~2800 km por encima o por debajo del plano orbital de Thalassa en su aproximación más cercana. Como es común, esta resonancia estabiliza las órbitas al maximizar la separación en la conjunción, pero es inusual por el papel que juega la inclinación orbital para facilitar esta evasión en un caso donde las excentricidades son mínimas.
Resonancias de movimiento medio entre planetas extrasolares
Si bien no se ha encontrado que la mayoría de los sistemas planetarios extrasolares descubiertos tengan planetas en resonancias de movimiento medio, se han descubierto cadenas de hasta cinco planetas resonantes y hasta siete al menos planetas cercanos a la resonancia. Las simulaciones han demostrado que durante la formación del sistema planetario, la presencia del disco de gas primordial favorece la aparición de cadenas resonantes de embriones planetarios. Una vez que ese gas se disipa, el 90-95% de esas cadenas deben volverse inestables para igualar la baja frecuencia de las cadenas resonantes observadas.
- Como se mencionó anteriormente, Gliese 876 e, b y c están en una resonancia de Laplace, con una relación 4:2:1 de períodos (124.3, 61.1 y 30.0 días). En este caso, CCPR CCPR L{displaystyle ¿Qué? librados con una amplitud de 40° ± 13° y la resonancia sigue la relación media-tiempo:
- CCPR CCPR L=λ λ c− − 3⋅ ⋅ λ λ d+2⋅ ⋅ λ λ e=0∘ ∘ {displaystyle Phi _{L}=lambda _{rm {c}-3cdot lambda ¿Por qué? }
- Kepler-223 tiene cuatro planetas en una resonancia con una relación de órbita 8:6:4:3 y una relación de 3:4:6:8 de períodos (7.3845, 9.8456, 14.7887 y 19.7257 días). Esto representa la primera resonancia orbital confirmada de 4 cuerpos. Las libraciones dentro de este sistema son tales que los encuentros cercanos entre dos planetas ocurren sólo cuando los otros planetas están en partes distantes de sus órbitas. Las simulaciones indican que este sistema de resonancias debe haberse formado a través de la migración planetaria.
- Kepler-80 d, e, b, c y g tienen períodos en un ~ 1.000: 1.512: 2.296: 3.100: 4.767 ratio (3.0722, 4.6449, 7.0525, 9.5236 y 14.6456 días). Sin embargo, en un marco de referencia que gira con las conjunciones, esto reduce a una relación de período de 4:6:9:12:18 (una relación de órbita de 9:6:4:3:2). Conjunciones de d y e, e y b, b y c, y c y g ocurren a intervalos relativos de 2:3:6 (9.07, 13.61 y 27.21 días) en un patrón que repite alrededor de cada 190.5 días (siete ciclos completos en el marco giratorio) en el marco inercial o no rotativo (equivalente a 62:41:27:13 resonancia de la relación de órbita noro Las vibraciones de posibles resonancias de tres cuerpos tienen amplitudes de sólo unos 3 grados, y el modelado indica que el sistema resonante es estable para las perturbaciones. No ocurren conjunciones triples.
- TOI-178 tiene 6 planetas confirmados, de los cuales los 5 planetas externos forman una cadena resonante similar en un marco rotativo de referencia, que puede ser expresado como 2:4:6:9:12 en relación de período, o como 18:9:6:4:3 en relación órbita. Además, el planeta más interior b con el período de 1.91d órbitas cercanas a donde también sería parte de la misma cadena de resonancia de Laplace, como una resonancia 3:5 con el planeta c se cumpliría en el período de ~1.95d, lo que implica que podría haber evolucionado allí pero sacó de la resonancia, posiblemente por fuerzas de marea.
- Los siete planetas aproximadamente de tamaño terrestre de TRAPPIST-1 están en una cadena de resonancias cercanas (la cadena más larga conocida), teniendo una relación orbital de aproximadamente 24, 15, 9, 6, 4, 3 y 2, o ratios de períodos de vecinos más cercanos (procediendo hacia fuera) de unos 8/5, 5/3, 3/2, 3/2, 4/3 y 3/2 (1.603, 1.672, 1.506, 1.519, 1.509). También están configurados de tal manera que cada triple de planetas adyacentes está en una resonancia Laplace (es decir, b, c y d en una configuración de Laplace tal; c, d y e en otro, etc.). Se espera que la configuración resonante sea estable a una escala temporal de miles de millones de años, suponiendo que surgiera durante la migración planetaria. Se ha proporcionado una interpretación musical de la resonancia.
- Kepler-29 tiene un par de planetas en una resonancia de 7:9 (ratio de 1/1.28587).
- Kepler-36 tiene un par de planetas cerca de una resonancia de 6:7.
- Kepler-37 d, c y b están dentro del uno por ciento de una resonancia con una relación de órbita de 8:15:24 y una relación de 15:8:5 de los períodos (39.792187, 21.301886 y 13.367308 días).
- De los ocho planetas conocidos de Kepler-90, las ratios de período b:c, c:i y i:d están cerca de 4:5, 3:5 y 1:4, respectivamente (4:4.977, 3:4.97 y 1:4.13) y d, e, f, g y h están cerca de una relación de periodo 2:3:4:7:11 (2: 3.078: 4.182: 7.051: 11.102; también 7: 11.02 h) f Relevant to systems like this and that of Kepler-36, calculations suggest that the presence of an outer gas gigante planet facilitates the formation of closely packed resonances among inside super-Earths.
- HD 41248 tiene un par de super-Earths dentro del 0,3% de una resonancia 5:7 (ratio de 1/1.39718).
- K2-138 tiene 5 planetas confirmados en una cadena de resonancia no rota cerca de 3:2 (con períodos de 2.353, 3.560, 5.405, 8.261 y 12.758 días). El sistema fue descubierto en el proyecto científico ciudadano Exoplanet Explorers, utilizando datos K2. K2-138 podría albergar cuerpos co-orbitales (en una resonancia media-moción 1:1). Los sistemas de cadena resonantes pueden estabilizar los cuerpos coorbitales y un análisis específico de la curva de luz K2 y la velocidad radial de HARPS podrían revelarlos. Las observaciones de seguimiento con el Telescopio Espacial Spitzer sugieren que un sexto planeta continúe con la cadena de resonancia 3:2, dejando dos lagunas en la cadena (su período es de 41.97 días). Estas brechas podrían ser llenadas por pequeños planetas no transitorios. Las futuras observaciones con CHEOPS medirán las variaciones que estimulan el tránsito del sistema para seguir analizando la masa de los planetas y podrían potencialmente encontrar otros cuerpos planetarios en el sistema.
- K2-32 tiene cuatro planetas en una resonancia cercana a 1:2:5:7 (con períodos de 4.34, 8.99, 20.66 y 31.71 días). Planeta e tiene un radio casi idéntico al de la Tierra. Los otros planetas tienen un tamaño entre Neptuno y Saturno.
- V1298 Tauri tiene cuatro planetas confirmados de los cuales los planetas c, d y b están cerca de una resonancia 1:2:3 (con períodos de 8.25, 12.40 y 24.14 días). El Planeta e sólo muestra un solo tránsito en la curva de luz K2 y tiene un período superior a 36 días. Planeta e podría estar en una resonancia de orden bajo (de 2:3, 3:5, 1:2, o 1:3) con el planeta b. El sistema es muy joven (23±4 Myr) y podría ser un precursor de un sistema multiplanet compacto. La resonancia 2:3 sugiere que algunos planetas cercanos pueden formar en resonancias o evolucionar hacia ellos en escalas temporales de menos de 10 Mir. Los planetas del sistema tienen un tamaño entre Neptuno y Saturno. Sólo el planeta b tiene un tamaño similar a Júpiter.
- HD 158259 contiene cuatro planetas en una cadena de resonancia cerca de 3:2 (con períodos de 3.432, 5.198, 7.954 y 12.03 días, o ratios de período de 1,51, 1,53 y 1,51, respectivamente), con un posible quinto planeta también cerca de una resonancia de 3:2 (con un período de 17,4 días). Los exoplanetas fueron encontrados con el espectrógrafo Echelle SOPHIE, utilizando el método de velocidad radial.
- Kepler-1649 contiene dos planetas de tamaño terrestre cerca de una resonancia 9:4 (con períodos de 19.53527 y 8.689099 días, o una relación de periodo de 2.24825), incluyendo uno ("c") en la zona habitable. Un planeta no detectado con un período de 13.0 días crearía una cadena de resonancia 3:2.
- Kepler-88 tiene un par de planetas interiores cercanos a una resonancia 1:2 (ratio de periodo de 2.0396), con una relación de masa de ~22.5, produciendo variaciones de tiempo de tránsito muy grandes de ~0.5 días para el planeta más interno. Hay un planeta exterior aún más masivo en una órbita de ~1400 días.
Los casos de planetas extrasolares cercanos a una resonancia de movimiento medio de 1:2 son bastante comunes. Se informa que el dieciséis por ciento de los sistemas encontrados por el método de tránsito tienen un ejemplo de esto (con relaciones de período en el rango de 1,83 a 2,18), así como una sexta parte de los sistemas planetarios caracterizados por espectroscopia Doppler (con en este caso una relación de período más estrecha alcance). Debido al conocimiento incompleto de los sistemas, es probable que las proporciones reales sean mayores. En general, alrededor de un tercio de los sistemas caracterizados por velocidad radial parecen tener un par de planetas cercanos a una conmensurabilidad. Es mucho más común que los pares de planetas tengan proporciones de periodos orbitales un poco por ciento más grandes que una proporción de resonancia de movimiento medio que un poco por ciento más pequeñas (particularmente en el caso de resonancias de primer orden, en las que los números enteros en la proporción difieren en uno).). Se predijo que esto sería cierto en los casos en que las interacciones de las mareas con la estrella fueran significativas.
Casual 'cerca' proporciones de movimiento medio

A veces se señala una serie de relaciones de proporciones casi enteras entre las frecuencias orbitales de los planetas o lunas principales (consulte la lista a continuación). Sin embargo, estos no tienen importancia dinámica porque no hay una precesión apropiada del perihelio u otra libración para hacer que la resonancia sea perfecta (ver la discusión detallada en la sección anterior). Tales resonancias cercanas son dinámicamente insignificantes incluso si el desajuste es bastante pequeño porque (a diferencia de una resonancia verdadera), después de cada ciclo, la posición relativa de los cuerpos cambia. Cuando se promedia en escalas de tiempo astronómicamente cortas, su posición relativa es aleatoria, al igual que los cuerpos que no están cerca de la resonancia. Por ejemplo, considere las órbitas de la Tierra y Venus, que llegan a casi la misma configuración después de 8 órbitas terrestres y 13 órbitas de Venus. La relación real es 0,61518624, que está a solo un 0,032 % de distancia de exactamente 8:13. El desajuste después de 8 años es de solo 1,5° de Venus' movimiento orbital. Aún así, esto es suficiente para que Venus y la Tierra se encuentren en la orientación relativa opuesta a la original cada 120 ciclos de este tipo, que son 960 años. Por lo tanto, en escalas de tiempo de miles de años o más (aún diminutas según los estándares astronómicos), su posición relativa es efectivamente aleatoria.
La presencia de una resonancia cercana puede reflejar que existió una resonancia perfecta en el pasado, o que el sistema está evolucionando hacia una en el futuro.
Algunas coincidencias de frecuencia orbital incluyen:
| (Ratio) and bodies | Mismatch después de un ciclo | Hora de azar | Probabilidad |
|---|---|---|---|
| Planetas | |||
| (9:23) Venus–Mercury | 4.0° | 200 y | 0.19 |
| (8:13) Tierra – Venus | 1,5° | 1000 y | 0,065 |
| (243:395) Tierra–Venus | 0,8° | 50.000 y | 0,688 |
| (1:3) Marte–Venus | 20,6° | 20 y | 0.11 |
| (1:2) Marte – Tierra | 42.9° | 8 y | 0,244 |
| (1:12) Júpiter – Tierra | 49.1° | 40 y | 0,28 |
| (2:5) Saturno – Júpiter | 12,8° | 800 y | 0,13 |
| (1:7) Urano – Júpiter | 31.1° | 500 y | 0.18 |
| (7:20) Urano–Saturn | 5,7° | 20.000 y | 0.20 |
| (5:28) Neptuno–Saturn | 1.9° | 80.000 y | 0,052 |
| (1:2) Neptuno-Uranus | 14.0° | 2000 y | 0,078 |
| Sistema Marte | |||
| (1:4) Deimos–Phobos | 14.9° | 0,04 y | 0,083 |
| Principales asteroides | |||
| (1:1) Pallas–Ceres | 0,7° | 1000 y | 0,0039 |
| (7:18) Júpiter-Pallas | 0,10° | 100.000 y | 0,0040 |
| 87 Sistema Sylvia | |||
| (17:45) Romulus–Remus | 0,7° | 40 y | 0,067 |
| Sistema Júpiter | |||
| (1:6) Io-Metis | 0,6° | 2 y | 0,0031 |
| (3:5) Amalthea–Adrastea | 3,9° | 0.2 y | 0,064 |
| (3:7) Callisto-Ganymede | 0,7° | 30 y | 0,012 |
| Sistema Saturno | |||
| (2:3) Enceladus–Mimas | 33.2° | 0,04 y | 0.33 |
| (2:3) Dione-Tethys | 36.2° | 0,07 y | 0.36 |
| (3:5) Ñandú-Dione | 17.1° | 0.4 y | 0,266 |
| (2:7) Titan-Rhea | 21.0° | 0.7 y | 0.22 |
| (1:5) Iapetus-Titan | 9.2° | 4 y | 0,051 |
| Principales centaurios | |||
| (3:4) Urano-Chariklo | 4.5° | 10.000 y | 0,073 |
| Sistema de Urano | |||
| (3:5) Rosalind-Cordelia | 0.22° | 4 y | 0,0037 |
| (1:3) Umbriel-Miranda | 24,5° | 0,08 y | 0.14 |
| (3:5) Umbriel-Ariel | 24.2° | 0.3 y | 0,355 |
| (1:2) Titania-Umbriel | 36.3° | 0.1 y | 0.20 |
| (2:3) Oberon-Titania | 33,4° | 0.4 y | 0.34 |
| Sistema Neptuno | |||
| (1:20) Triton-Naiad | 13.5° | 0.2 y | 0,075 |
| (1:2) Proteus-Larissa | 8,4° | 0,07 y | 0,047 |
| (5:6) Proteus-Hippocamp | 2.1° | 1 y | 0,057 |
| Sistema Plutón | |||
| (1:3) Styx-Charon | 58,5° | 0.2 y | 0.33 |
| (1:4) Nix–Charon | 39,1° | 0.3 y | 0.22 |
| (1:5) Kerberos–Charon | 9.2° | 2 y | 0,05 |
| (1:6) Hydra-Charon | 6.6° | 3 y | 0,037 |
| Sistema Haumea | |||
| (3:8) Hiiaka–Namaka | 42,5° | 2 y | 0,555 |
- ^ Mismatch en longitud orbital del cuerpo interior, en comparación con su posición al comienzo del ciclo (con el ciclo definido como n órbitas del cuerpo exterior – ver abajo). Se asumen órbitas circulares (es decir, se ignora la precesión).
- ^ El tiempo necesario para que el desajuste de las posiciones orbitales longitudinales iniciales de los cuerpos crezca a 180°, redondeado al primer dígito significativo más cercano.
- ^ La probabilidad de obtener una coincidencia orbital de igual o menor desajuste por casualidad al menos una vez n intentos, donde n es el número entero de órbitas del cuerpo exterior por ciclo, y se supone que el desajuste varía entre 0° y 180° al azar. El valor se calcula como 1- (1- desajuste/180°)n. Este es un cálculo crudo que sólo intenta dar una idea áspera de probabilidades relativas.
- ^ Las dos comunidades cercanas enumeradas para la Tierra y Venus se reflejan en el momento de tránsitos de Venus, que ocurren en pares de 8 años de distancia, en un ciclo que repite cada 243 años.
- ^ La resonancia cercana 1:12 entre Júpiter y la Tierra hace que los asteroides Alinda, que ocupan (o están cerca) la resonancia 3:1 con Júpiter, estén cerca de una resonancia 1:4 con la Tierra.
- ^ Esta resonancia cercana ha sido calificada Gran calidad. Fue descrito por primera vez por Laplace en una serie de artículos publicados 1784-1789.
- ^ Es probable que las resonancias con una luna interior ahora desaparecida hayan estado involucradas en la formación de Phobos y Deimos.
- ^ Basado en los períodos orbitales apropiados, 1684.869 y 1681.601 días, para Pallas y Ceres, respectivamente.
- ^ Basado en el período orbital adecuado de Pallas, 1684.869 días, y 4332.59 días para Júpiter.
- ^ 87 Sylvia es el primer asteroide descubierto que tiene más de una luna.
- ^ Esta resonancia puede haber sido ocupada en el pasado.
- ^ Algunas definiciones de centauros estipulan que son órganos no resonantes.
- ^ Esta resonancia puede haber sido ocupada en el pasado.
- ^ Esta resonancia puede haber sido ocupada en el pasado.
- ^ Los resultados para el sistema Haumea no son muy significativos porque, contrariamente a las suposiciones implícitas en los cálculos, Namaka tiene una órbita excéntrica y no bajista que precede rápidamente (ver abajo). Hi-iaka y Namaka están mucho más cerca de una resonancia de 3:8 de lo indicado, y puede estar realmente en ella.
La correlación orbital menos probable de la lista es la que existe entre Io y Metis, seguida de las que existen entre Rosalinda y Cordelia, Palas y Ceres, Júpiter y Palas, Calisto y Ganímedes, e Hidra y Caronte, respectivamente.
Posibles resonancias pasadas de movimiento medio
Una resonancia pasada entre Júpiter y Saturno puede haber jugado un papel dramático en la historia temprana del Sistema Solar. Un modelo de computadora de 2004 de Alessandro Morbidelli del Observatoire de la Côte d'Azur en Niza sugirió la formación de una resonancia 1: 2 entre Júpiter y Saturno debido a interacciones con planetesimales que los hicieron migrar hacia adentro y hacia afuera, respectivamente. En el modelo, esto creó un empuje gravitacional que impulsó tanto a Urano como a Neptuno a órbitas más altas y, en algunos escenarios, hizo que cambiaran de lugar, lo que habría duplicado la distancia de Neptuno al Sol. La expulsión resultante de objetos del cinturón proto-Kuiper cuando Neptuno se movió hacia afuera podría explicar el Bombardeo Intenso Tardío 600 millones de años después de la formación del Sistema Solar y el origen de los asteroides troyanos de Júpiter. Una migración hacia el exterior de Neptuno también podría explicar la ocupación actual de algunas de sus resonancias (particularmente la resonancia 2:5) dentro del cinturón de Kuiper.
Si bien las lunas medianas de Saturno, Dione y Tethys, no están cerca de una resonancia exacta ahora, es posible que hayan estado en una resonancia 2:3 al principio de la historia del Sistema Solar. Esto habría llevado a la excentricidad orbital y al calentamiento de las mareas que podrían haber calentado a Tethys' lo suficientemente interior como para formar un océano subterráneo. La congelación posterior del océano después de que las lunas escaparan de la resonancia puede haber generado las tensiones de extensión que crearon el enorme sistema de fosas de Ithaca Chasma en Tethys.
El sistema de satélites de Urano es notablemente diferente de los de Júpiter y Saturno en que carece de resonancias precisas entre las lunas más grandes, mientras que la mayoría de las lunas más grandes de Júpiter (3 de las 4 más grandes) y de Saturno (6 de los 8 más grandes) están en resonancias de movimiento medio. En los tres sistemas de satélites, las lunas probablemente fueron capturadas en resonancias de movimiento medio en el pasado cuando sus órbitas cambiaron debido a la disipación de las mareas, un proceso por el cual los satélites ganan energía orbital a expensas de la energía de rotación primaria, lo que afecta el interior. lunas desproporcionadamente. En el sistema de Urano, sin embargo, debido al menor grado de achatamiento del planeta y al mayor tamaño relativo de sus satélites, escapar de una resonancia de movimiento medio es mucho más fácil. El menor achatamiento del primario altera su campo gravitatorio de tal manera que las diferentes resonancias posibles se espacian más juntas. Un tamaño de satélite relativo más grande aumenta la fuerza de sus interacciones. Ambos factores conducen a un comportamiento orbital más caótico en o cerca de las resonancias de movimiento medio. El escape de una resonancia puede estar asociado con la captura en una resonancia secundaria y/o aumentos impulsados por la evolución de las mareas en la excentricidad o inclinación orbital.
Las resonancias de movimiento medio que probablemente alguna vez existieron en el Sistema de Urano incluyen (3:5) Ariel-Miranda, (1:3) Umbriel-Miranda, (3:5) Umbriel-Ariel y (1:4) Titania -Ariel. La evidencia de tales resonancias pasadas incluye las excentricidades relativamente altas de las órbitas de Urano & # 39; satélites interiores, y la inclinación orbital anómalamente alta de Miranda. Las excentricidades orbitales del pasado alto asociadas con las resonancias (1: 3) Umbriel-Miranda y (1: 4) Titania-Ariel pueden haber llevado al calentamiento de las mareas en los interiores de Miranda y Ariel, respectivamente. Miranda probablemente escapó de su resonancia con Umbriel a través de una resonancia secundaria, y se cree que el mecanismo de este escape explica por qué su inclinación orbital es más de 10 veces mayor que la de las otras lunas regulares de Urano (ver los satélites naturales de Urano).
Al igual que en el caso de Miranda, se cree que las inclinaciones actuales de las pequeñas lunas de Júpiter, Amaltea y Tebe, son indicaciones de un pasado pasado a través de las resonancias 3:1 y 4:2 con Io, respectivamente.
Se cree que las lunas regulares de Neptuno, Proteo y Larisa, pasaron por una resonancia 1:2 hace unos cientos de millones de años; las lunas se han alejado unas de otras desde entonces porque Proteus está fuera de una órbita síncrona y Larissa está dentro de una. Se cree que el paso a través de la resonancia excitó a ambas lunas. excentricidades a un grado que desde entonces no se ha amortiguado por completo.
En el caso de los satélites de Plutón, se ha propuesto que las resonancias cercanas actuales son reliquias de una resonancia precisa previa que fue interrumpida por la amortiguación de la excentricidad de la órbita de Caronte por las mareas (ver Plutón's). 39;s satélites naturales para más detalles). Las resonancias cercanas pueden ser mantenidas por una fluctuación local del 15% en el campo gravitatorio de Plutón-Caronte. Por lo tanto, estas resonancias cercanas pueden no ser una coincidencia.
La luna interior más pequeña del planeta enano Haumea, Namaka, tiene una décima parte de la masa de la luna exterior más grande, Hiʻiaka. Namaka gira alrededor de Haumea en 18 días en una órbita excéntrica no kepleriana y, a partir de 2008, tiene una inclinación de 13 ° desde Hiʻiaka. Durante la escala de tiempo del sistema, debería haber sido amortiguado por las mareas en una órbita más circular. Parece que ha sido perturbado por resonancias con el más masivo Hiʻiaka, debido a las órbitas convergentes a medida que se alejaba de Haumea debido a la disipación de las mareas. Las lunas pueden haber quedado atrapadas y luego escaparon de la resonancia orbital varias veces. Probablemente pasaron por la resonancia 3:1 hace relativamente poco tiempo, y actualmente están en o al menos cerca de una resonancia 8:3. La órbita de Namaka está fuertemente perturbada, con una precesión actual de alrededor de -6,5° por año.
Contenido relacionado
Neutronio
Astronomía infrarroja
Viscosímetro