Relleno de cifrado asimétrico óptimo

En criptografía, el relleno de cifrado asimétrico óptimo (OAEP) es un esquema de relleno que se utiliza a menudo junto con el cifrado RSA. Bellare y Rogaway introdujeron OAEP y posteriormente lo estandarizaron en PKCS#1 v2 y RFC 2437.

El algoritmo OAEP es una forma de red Feistel que utiliza un par de oráculos aleatorios G y H para procesar el texto claro antes de la encriptación asimétrica. Cuando se combina con cualquier trampolín seguro permutación f{displaystyle f}, este procesamiento se prueba en el modelo oráculo aleatorio para dar lugar a un esquema combinado que es semánticamente seguro bajo ataque de texto escogido (IND-CPA). Cuando se implementa con ciertas permutaciones de trampolín (por ejemplo, RSA), OAEP también se demuestra que está segura contra el ataque de cifertexto elegido. OAEP se puede utilizar para construir una transformación de todo o nada.

La OAEP satisface los dos objetivos siguientes:

1. Añadir un elemento de aleatoriedad que se puede utilizar para convertir un esquema de encriptación determinista (por ejemplo, RSA tradicional) en un esquema probabilístico.
2. Prevenir el desciframiento parcial de los cifertextos (o otras fugas de información) asegurando que un adversario no pueda recuperar ninguna parte del texto sin poder invertir la permutación del trampolín f{displaystyle f}.

La versión original de OAEP (Bellare/Rogaway, 1994) mostró una forma de "conciencia de texto plano" (que, según afirmaron, implica seguridad contra el ataque de texto cifrado elegido) en el modelo de oráculo aleatorio cuando se utiliza OAEP con cualquier permutación de trampilla. Los resultados posteriores contradijeron esta afirmación y mostraron que OAEP solo era seguro para IND-CCA1. Sin embargo, se demostró que el esquema original en el modelo aleatorio de Oracle es seguro IND-CCA2 cuando se usa OAEP con la permutación RSA utilizando exponentes de cifrado estándar, como en el caso de RSA-OAEP. Victor Shoup ofreció un esquema mejorado (llamado OAEP+) que funciona con cualquier permutación unidireccional de trampilla para resolver este problema. Un trabajo más reciente ha demostrado que en el modelo estándar (es decir, cuando las funciones hash no se modelan como oráculos aleatorios) es imposible probar la seguridad IND-CCA2 de RSA-OAEP bajo la supuesta dureza del problema RSA.

Algoritmo

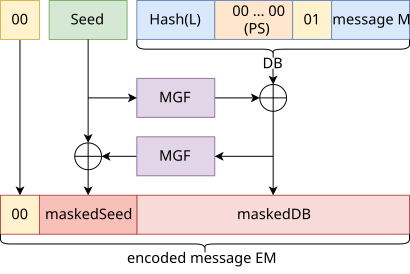
En el diagrama,

• MGF es la función generadora de máscaras, generalmente MGF1,
• Hash es la función hash elegida,
• h Len es la longitud de la salida de la función hash en bytes,
• k es la longitud del módulo RSA n en bytes,
• M es el mensaje a remar (en la mayoría k− − 2⋅ ⋅ hLen− − 2{displaystyle k-2cdot mathrm {hLen} -2} bytes),
• L es una etiqueta opcional que se asocia con el mensaje (la etiqueta es la cadena vacía por defecto y se puede utilizar para autenticar datos sin necesidad de encriptación),
• PS es una cadena de byte k− − mLen− − 2⋅ ⋅ hLen− − 2{displaystyle k-mathrm {mLen} -2cdot mathrm {hLen} -2} null-bytes.
• ⊕ es una XOR-Operación.

Codificación

RFC 8017 para PKCS#1 v2.2 especifica el esquema OAEP de la siguiente manera para la codificación:

1. Hash la etiqueta L usando la función hash elegida: lHash=Hash()L){displaystyle mathrm {lHash} =mathrm {Hash} (L)}
2. Generar una cadena de relleno PS consistente en k− − mLen− − 2⋅ ⋅ hLen− − 2{displaystyle k-mathrm {mLen} -2cdot mathrm {hLen} -2} bytes con el valor 0x00.
3. Concatenate lHash, PS, el único byte 0x01, y el mensaje M para formar un bloque de datos DB: DB=lHashSilencioSilencioPSSilencioSilencio0x01SilencioSilencioM{displaystyle mathrm {DB} =mathrm {lHash}. Este bloque de datos tiene longitud k− − hLen− − 1{displaystyle k-mathrm {hLen} -1} bytes.
4. Generar una semilla aleatoria de longitud h Len.
5. Utilice la función generadora de máscaras para generar una máscara de la longitud adecuada para el bloque de datos: dbMask=MGF()seed,k− − hLen− − 1){displaystyle mathrm {dbMask} =mathrm {MGF} (mathrm {seed}k-mathrm {hLen} -1)}
6. Máscara el bloque de datos con la máscara generada: maskedDB=DB⊕ ⊕ dbMask{displaystyle mathrm {masked DB} =mathrm {DB} oplus mathrm {dbMask}
7. Utilice la función generadora de máscaras para generar una máscara de longitud h Len para la semilla: seedMask=MGF()maskedDB,hLen){displaystyle mathrm {seed Mask} =mathrm {MGF} (mathrm {maskedDB}mathrm {hLen})}
8. Máscara la semilla con la máscara generada: maskedSeed=seed⊕ ⊕ seedMask{displaystyle mathrm {masked Seed} =mathrm {seed} oplus mathrm {seed Máscara
9. El mensaje codificado (pagado) es el byte 0x00 concatenado con el máscarasSeed y enmascaradoDB: EM=0x00SilencioSilenciomaskedSeedSilencioSilenciomaskedDB{displaystyle mathrm {EM} =mathrm {0x00} Semillas. DB}

Decodificación

La decodificación funciona invirtiendo los pasos seguidos en el algoritmo de codificación:

1. Hash la etiqueta L usando la función hash elegida: lHash=Hash()L){displaystyle mathrm {lHash} =mathrm {Hash} (L)}
2. Para revertir el paso 9, dividir el mensaje codificado EM en el byte 0x00, el máscarasSeed (con longitud) h Len) y el enmascaradoDB: EM=0x00SilencioSilenciomaskedSeedSilencioSilenciomaskedDB{displaystyle mathrm {EM} =mathrm {0x00} Semillas. DB}
3. Generar el semillas Máscara que se usó para enmascarar semillas: seedMask=MGF()maskedDB,hLen){displaystyle mathrm {seed Mask} =mathrm {MGF} (mathrm {maskedDB}mathrm {hLen})}
4. Para revertir el paso 8, recuperar el semillas con el semillas Máscara: seed=maskedSeed⊕ ⊕ seedMask{displaystyle mathrm {seed} =mathrm {masked Seed} oplus mathrm {seed Máscara
5. Generar el dbMask que se utilizó para ocultar el bloque de datos: dbMask=MGF()seed,k− − hLen− − 1){displaystyle mathrm {dbMask} =mathrm {MGF} (mathrm {seed}k-mathrm {hLen} -1)}
6. Para revertir el paso 6, recuperar el bloque de datos DB: DB=maskedDB⊕ ⊕ dbMask{displaystyle mathrm {DB} =mathrm {maskedDB} oplus mathrm {dbMask}
7. Para revertir el paso 3, dividir el bloque de datos en sus partes: DB=lHash.SilencioSilencioPSSilencioSilencio0x01SilencioSilencioM{displaystyle mathrm {DB} =mathrm {lHash'} Silencio eternamathrm {PS}.
   1. Verificar que:
      • lHash ' es igual al computado lHash
      • PS sólo consta de bytes 0x00
      • PS y M están separados por el byte 0x01 y
      • el primer byte de EM es el byte 0x00.
   2. Si alguna de estas condiciones no se cumplen, entonces el relleno es inválido.

Uso en RSA: El mensaje codificado se puede encriptar con RSA. La propiedad determinista de RSA ahora se evita utilizando la codificación OAEP porque la semillas se genera aleatoriamente e influye en todo el mensaje codificado.

Seguridad

El "todo o nada" la seguridad proviene del hecho de que para recuperar C:, uno debe recuperar toda la DB y toda la Seed; Se requiere DB para recuperar la semilla de la Semilla, y se requiere la semilla para recuperar el bloque de datos DB de DB. Dado que cualquier bit modificado de un hash criptográfico cambia completamente el resultado, toda la DB y toda la Seed deben recuperarse por completo.

Implementación

En el estándar PKCS#1, los oráculos aleatorios son idénticos. El estándar PKCS#1 requiere además que los oráculos aleatorios sean MGF1 con una función hash adecuada.