Relatividad general

La relatividad general, también conocida como teoría general de la relatividad y teoría de la gravedad de Einstein, es la teoría geométrica de gravitación publicado por Albert Einstein en 1915 y es la descripción actual de la gravitación en la física moderna. La relatividad general generaliza la relatividad especial y refina la ley de gravitación universal de Newton, proporcionando una descripción unificada de la gravedad como una propiedad geométrica del espacio y el tiempo o espacio-tiempo de cuatro dimensiones. En particular, la curvatura del espacio-tiempo está directamente relacionada con la energía y el momento de cualquier materia y radiación presentes. La relación se especifica mediante las ecuaciones de campo de Einstein, un sistema de ecuaciones diferenciales parciales de segundo orden.

La ley de gravitación universal de Newton, que describe la gravedad clásica, puede verse como una predicción de la relatividad general para la geometría del espacio-tiempo casi plana alrededor de distribuciones de masa estacionarias. Algunas predicciones de la relatividad general, sin embargo, están más allá de la ley de gravitación universal de Newton en la física clásica. Estas predicciones se refieren al paso del tiempo, la geometría del espacio, el movimiento de los cuerpos en caída libre y la propagación de la luz, e incluyen la dilatación del tiempo gravitacional, la lente gravitatoria, el corrimiento al rojo gravitatorio de la luz, el retraso de tiempo de Shapiro y singularidades/negro agujeros Hasta ahora, se ha demostrado que todas las pruebas de la relatividad general están de acuerdo con la teoría. Las soluciones dependientes del tiempo de la relatividad general nos permiten hablar sobre la historia del universo y han proporcionado el marco moderno para la cosmología, lo que llevó al descubrimiento del Big Bang y la radiación cósmica de fondo de microondas. A pesar de la introducción de una serie de teorías alternativas, la relatividad general sigue siendo la teoría más simple consistente con los datos experimentales.

Sin embargo, la reconciliación de la relatividad general con las leyes de la física cuántica sigue siendo un problema, ya que falta una teoría autoconsistente de la gravedad cuántica. Aún no se sabe cómo se puede unificar la gravedad con las tres fuerzas no gravitatorias: fuerte, débil y electromagnética.

La teoría de Einstein tiene implicaciones astrofísicas, incluida la predicción de agujeros negros, regiones del espacio en las que el espacio y el tiempo están distorsionados de tal manera que nada, ni siquiera la luz, puede escapar de ellos. Los agujeros negros son el estado final de las estrellas masivas. Se cree que los microquásares y los núcleos galácticos activos son agujeros negros estelares y agujeros negros supermasivos. También predice lentes gravitacionales, donde la curvatura de la luz da como resultado múltiples imágenes del mismo fenómeno astronómico distante. Otras predicciones incluyen la existencia de ondas gravitacionales, que han sido observadas directamente por la colaboración física LIGO y otros observatorios. Además, la relatividad general ha proporcionado la base de los modelos cosmológicos de un universo en expansión.

En el prefacio de Relativity: The Special and the General Theory, Einstein dijo: "El presente libro pretende, en la medida de lo posible, dar una idea exacta de la teoría de la relatividad a aquellos lectores que, desde un punto de vista punto de vista científico y filosófico general, están interesados en la teoría, pero que no están familiarizados con el aparato matemático de la física teórica. La obra supone un nivel de educación correspondiente al de un examen de matriculación universitaria y, a pesar de la brevedad del libro, una buena cantidad de paciencia y fuerza de voluntad por parte del lector. El autor no ha escatimado esfuerzos en su esfuerzo por presentar las ideas principales en la forma más simple e inteligible y, en conjunto, en la secuencia y conexión en las que realmente se originaron."

Ampliamente reconocida como una teoría de extraordinaria belleza, la relatividad general se ha descrito a menudo como la más hermosa de todas las teorías físicas existentes.

Historia

Poco después de publicar la teoría especial de la relatividad en 1905, Einstein comenzó a pensar en cómo incorporar la gravedad en su nuevo marco relativista. En 1907, comenzando con un experimento mental simple que involucraba a un observador en caída libre, se embarcó en lo que sería una búsqueda de ocho años para una teoría relativista de la gravedad. Después de numerosos desvíos y comienzos en falso, su trabajo culminó con la presentación a la Academia de Ciencias de Prusia en noviembre de 1915 de lo que ahora se conoce como las ecuaciones de campo de Einstein, que forman el núcleo de la teoría general de la relatividad de Einstein. Estas ecuaciones especifican cómo la geometría del espacio y el tiempo está influenciada por la materia y la radiación presentes. Una versión de la geometría no euclidiana, llamada Geometría de Riemann, permitió a Einstein desarrollar la relatividad general al proporcionar el marco matemático clave en el que encajaba sus ideas físicas de la gravedad. Esta idea fue señalada por el matemático Marcel Grossmann y publicada por Grossmann y Einstein en 1913.

Las ecuaciones de campo de Einstein no son lineales y se consideran difíciles de resolver. Einstein usó métodos de aproximación para elaborar las predicciones iniciales de la teoría. Pero en 1916, el astrofísico Karl Schwarzschild encontró la primera solución exacta no trivial para las ecuaciones de campo de Einstein, la métrica de Schwarzschild. Esta solución sentó las bases para la descripción de las etapas finales del colapso gravitacional y los objetos conocidos hoy como agujeros negros. En el mismo año, se dieron los primeros pasos para generalizar la solución de Schwarzschild a objetos cargados eléctricamente, lo que eventualmente resultó en la solución Reissner-Nordström, que ahora se asocia con agujeros negros cargados eléctricamente. En 1917, Einstein aplicó su teoría al universo como un todo, iniciando el campo de la cosmología relativista. De acuerdo con el pensamiento contemporáneo, asumió un universo estático, agregando un nuevo parámetro a sus ecuaciones de campo originales, la constante cosmológica, para que coincida con esa suposición observacional. Sin embargo, en 1929, el trabajo de Hubble y otros había demostrado que nuestro universo se está expandiendo. Esto se describe fácilmente mediante las soluciones cosmológicas en expansión encontradas por Friedmann en 1922, que no requieren una constante cosmológica. Lemaître utilizó estas soluciones para formular la primera versión de los modelos del Big Bang, en los que nuestro universo ha evolucionado desde un estado anterior extremadamente caliente y denso. Más tarde, Einstein declaró que la constante cosmológica era el mayor error de su vida.

Durante ese período, la relatividad general siguió siendo una especie de curiosidad entre las teorías físicas. Era claramente superior a la gravedad newtoniana, siendo consistente con la relatividad especial y teniendo en cuenta varios efectos no explicados por la teoría newtoniana. Einstein mostró en 1915 cómo su teoría explicaba el avance anómalo del perihelio del planeta Mercurio sin ningún parámetro arbitrario ("factores fudge"), y en 1919 una expedición dirigida por Eddington confirmó la predicción de la relatividad general para el desviación de la luz de las estrellas por el Sol durante el eclipse solar total del 29 de mayo de 1919, lo que instantáneamente hizo famoso a Einstein. Sin embargo, la teoría permaneció fuera de la corriente principal de la física teórica y la astrofísica hasta los desarrollos entre aproximadamente 1960 y 1975, ahora conocida como la edad de oro de la relatividad general. Los físicos comenzaron a comprender el concepto de agujero negro y a identificar los cuásares como uno de estos objetos. manifestaciones astrofísicas. Pruebas cada vez más precisas del sistema solar confirmaron el poder predictivo de la teoría, y la cosmología relativista también se volvió susceptible de pruebas de observación directa.

La relatividad general se ha ganado la reputación de ser una teoría de extraordinaria belleza. Subrahmanyan Chandrasekhar ha señalado que en múltiples niveles, la relatividad general exhibe lo que Francis Bacon ha denominado una "extrañeza en la proporción". (es decir. elementos que provocan asombro y sorpresa). Yuxtapone conceptos fundamentales (espacio y tiempo versus materia y movimiento) que antes se consideraban totalmente independientes. Chandrasekhar también señaló que las únicas guías de Einstein en su búsqueda de una teoría exacta eran el principio de equivalencia y su sentido de que una descripción adecuada de la gravedad debería ser geométrica en su base, de modo que hubiera un "elemento de revelación" en la forma en que Einstein llegó a su teoría. Otros elementos de belleza asociados con la teoría general de la relatividad son su simplicidad y simetría, la forma en que incorpora la invariancia y la unificación, y su perfecta consistencia lógica.

De la mecánica clásica a la relatividad general

La relatividad general se puede entender examinando sus similitudes y diferencias con la física clásica. El primer paso es darse cuenta de que la mecánica clásica y la ley de la gravedad de Newton admiten una descripción geométrica. La combinación de esta descripción con las leyes de la relatividad especial da como resultado una derivación heurística de la relatividad general.

Geometría de la gravedad newtoniana

Según la relatividad general, los objetos en un campo gravitacional se comportan de forma similar a los objetos dentro de un recinto acelerado. Por ejemplo, un observador verá una bola caer de la misma manera en un cohete (izquierda) como lo hace en la Tierra (derecha), siempre que la aceleración del cohete sea igual a 9,8 m/s² (la aceleración debido a la gravedad en la superficie de la Tierra).

En la base de la mecánica clásica se encuentra la noción de que el movimiento de un cuerpo se puede describir como una combinación de movimiento libre (o inercial) y desviaciones de este movimiento libre. Tales desviaciones son causadas por fuerzas externas que actúan sobre un cuerpo de acuerdo con la segunda ley del movimiento de Newton, que establece que la fuerza neta que actúa sobre un cuerpo es igual a la masa (inercial) de ese cuerpo multiplicada por su aceleración. Los movimientos de inercia preferidos están relacionados con la geometría del espacio y el tiempo: en los marcos de referencia estándar de la mecánica clásica, los objetos en movimiento libre se mueven a lo largo de líneas rectas a velocidad constante. En el lenguaje moderno, sus caminos son geodésicas, líneas rectas del mundo en un espacio-tiempo curvo.

Por el contrario, uno podría esperar que los movimientos de inercia, una vez identificados mediante la observación de los movimientos reales de los cuerpos y teniendo en cuenta las fuerzas externas (como el electromagnetismo o la fricción), puedan usarse para definir la geometría del espacio, así como una coordenada de tiempo. Sin embargo, existe una ambigüedad una vez que la gravedad entra en juego. De acuerdo con la ley de la gravedad de Newton, y verificada independientemente por experimentos como el de Eötvös y sus sucesores (ver el experimento de Eötvös), existe una universalidad de caída libre (también conocida como el principio de equivalencia débil, o la igualdad universal de masa inercial y pasivo-gravitacional): la trayectoria de un cuerpo de ensayo en caída libre depende únicamente de su posición y velocidad inicial, pero no de ninguna de sus propiedades materiales. Una versión simplificada de esto se materializa en el experimento del ascensor de Einstein, ilustrado en la figura de la derecha: para un observador en una habitación cerrada, es imposible decidir, mapeando la trayectoria de cuerpos como una pelota que se deja caer, ya sea que la habitación esté estacionaria en un campo gravitatorio y la pelota acelerando, o en el espacio libre a bordo de un cohete que acelera a una velocidad igual a la del campo gravitatorio contra la pelota que al soltarla tiene una aceleración nula.

Dada la universalidad de la caída libre, no existe una distinción observable entre el movimiento inercial y el movimiento bajo la influencia de la fuerza gravitacional. Esto sugiere la definición de una nueva clase de movimiento inercial, a saber, el de los objetos en caída libre bajo la influencia de la gravedad. Esta nueva clase de movimientos preferidos también define una geometría del espacio y el tiempo; en términos matemáticos, es el movimiento geodésico asociado con una conexión específica que depende del gradiente del potencial gravitacional. El espacio, en esta construcción, todavía tiene la geometría euclidiana ordinaria. Sin embargo, el espaciotiempo como un todo es más complicado. Como se puede demostrar utilizando experimentos mentales simples que siguen las trayectorias de caída libre de diferentes partículas de prueba, el resultado de transportar vectores de espacio-tiempo que pueden denotar la velocidad de una partícula (vectores similares al tiempo) variará con la velocidad de la partícula. trayectoria; matemáticamente hablando, la conexión newtoniana no es integrable. De esto, se puede deducir que el espacio-tiempo es curvo. La teoría resultante de Newton-Cartan es una formulación geométrica de la gravedad newtoniana que utiliza solo conceptos covariantes, es decir, una descripción que es válida en cualquier sistema de coordenadas deseado. En esta descripción geométrica, los efectos de marea, la aceleración relativa de los cuerpos en caída libre, están relacionados con la derivada de la conexión, mostrando cómo la geometría modificada es causada por la presencia de masa.

Generalización relativista

Cono de luz

Por intrigante que pueda ser la gravedad newtoniana geométrica, su base, la mecánica clásica, es simplemente un caso límite de la mecánica relativista (especial). En el lenguaje de la simetría: donde la gravedad puede despreciarse, la física es invariante de Lorentz como en la relatividad especial en lugar de invariante de Galilei como en la mecánica clásica. (La simetría definitoria de la relatividad especial es el grupo de Poincaré, que incluye traslaciones, rotaciones, impulsos y reflejos). Las diferencias entre los dos se vuelven significativas cuando se trata de velocidades cercanas a la velocidad de la luz y con fenómenos de alta energía.

Con la simetría de Lorentz, entran en juego estructuras adicionales. Están definidos por el conjunto de conos de luz (ver imagen). Los conos de luz definen una estructura causal: para cada evento A, hay un conjunto de eventos que pueden, en principio, influir o ser influenciados por A a través de señales o interacciones que no necesitan viajar más rápido que la luz (como el evento B en la imagen), y un conjunto de eventos para los cuales tales una influencia es imposible (como el evento C en la imagen). Estos conjuntos son independientes del observador. Junto con las líneas de mundo de partículas que caen libremente, los conos de luz se pueden usar para reconstruir la métrica semi-riemanniana del espacio-tiempo, al menos hasta un factor escalar positivo. En términos matemáticos, esto define una estructura conforme o geometría conforme.

La relatividad especial se define en ausencia de gravedad. Para aplicaciones prácticas, es un modelo adecuado siempre que se pueda despreciar la gravedad. Poniendo en juego la gravedad, y asumiendo la universalidad del movimiento de caída libre, se aplica un razonamiento análogo al de la sección anterior: no hay marcos inerciales globales. En cambio, hay marcos inerciales aproximados que se mueven junto con partículas que caen libremente. Traducido al lenguaje del espacio-tiempo: las líneas rectas similares al tiempo que definen un marco de inercia libre de gravedad se deforman en líneas curvas entre sí, lo que sugiere que la inclusión de la gravedad requiere un cambio en la geometría del espacio-tiempo.

A priori, no está claro si los nuevos marcos locales en caída libre coinciden con los marcos de referencia en los que se cumplen las leyes de la relatividad especial, esa teoría se basa en la propagación de la luz y, por lo tanto, en el electromagnetismo, que podría tener un conjunto diferente de marcos preferidos. Pero usando diferentes suposiciones sobre los marcos relativistas especiales (como que están fijos en la Tierra o en caída libre), uno puede derivar diferentes predicciones para el corrimiento al rojo gravitacional, es decir, la forma en que la frecuencia de la luz cambia a medida que la luz se propaga a través de un campo gravitatorio (cf. más abajo). Las medidas reales muestran que los marcos de caída libre son aquellos en los que la luz se propaga como lo hace en la relatividad especial. La generalización de esta afirmación, es decir, que las leyes de la relatividad especial tienen una buena aproximación en marcos de referencia en caída libre (y no giratorios), se conoce como el principio de equivalencia de Einstein, un principio rector crucial para generalizar la física relativista especial para incluir la gravedad..

Los mismos datos experimentales muestran que el tiempo medido por relojes en un campo gravitatorio (tiempo propio, para dar el término técnico) no sigue las reglas de la relatividad especial. En el lenguaje de la geometría del espacio-tiempo, no se mide con la métrica de Minkowski. Como en el caso newtoniano, esto sugiere una geometría más general. A escalas pequeñas, todos los marcos de referencia que están en caída libre son equivalentes y aproximadamente minkowskianos. En consecuencia, ahora estamos tratando con una generalización curva del espacio de Minkowski. El tensor métrico que define la geometría, en particular, cómo se miden las longitudes y los ángulos, no es la métrica de Minkowski de la relatividad especial, es una generalización conocida como métrica semi- o pseudo-riemanniana. Además, cada métrica riemanniana se asocia naturalmente con un tipo particular de conexión, la conexión Levi-Civita, y esta es, de hecho, la conexión que satisface el principio de equivalencia y hace que el espacio sea localmente minkowskiano (es decir, en coordenadas localmente inerciales adecuadas, la métrica es minkowskiana, y sus primeras derivadas parciales y los coeficientes de conexión desaparecen).

Ecuaciones de Einstein

Habiendo formulado la versión geométrica relativista de los efectos de la gravedad, la cuestión de la fuente de la gravedad permanece. En la gravedad newtoniana, la fuente es la masa. En la relatividad especial, la masa resulta ser parte de una cantidad más general llamada tensor de energía-cantidad de movimiento, que incluye densidades de energía y cantidad de movimiento, así como tensión: presión y corte. Usando el principio de equivalencia, este tensor se generaliza fácilmente al espacio-tiempo curvo. Profundizando en la analogía con la gravedad newtoniana geométrica, es natural suponer que la ecuación de campo de la gravedad relaciona este tensor con el tensor de Ricci, que describe una clase particular de efectos de marea: el cambio de volumen de una pequeña nube de partículas de prueba que están inicialmente en reposo y luego caen libremente. En relatividad especial, la conservación de la energía-momento corresponde a la afirmación de que el tensor de energía-momento está libre de divergencias. Esta fórmula también se generaliza fácilmente al espacio-tiempo curvo al reemplazar las derivadas parciales con sus contrapartes de variedades curvas, derivadas covariantes estudiadas en geometría diferencial. Con esta condición adicional (la divergencia covariante del tensor de energía-cantidad de movimiento, y por lo tanto de lo que sea que esté en el otro lado de la ecuación, es cero), el conjunto más simple de ecuaciones son las llamadas ecuaciones (de campo) de Einstein:

En el lado izquierdo está el tensor de Einstein, Gμ μ .. {displaystyle G_{munu}}, que es simétrico y una combinación específica sin divergencia del tensor Ricci Rμ μ .. {displaystyle R_{munu} y la métrica. En particular,

R=gμ μ .. Rμ μ .. {displaystyle R=g^{munu }R_{munu },}

es el escalar de curvatura. El tensor de Ricci en sí está relacionado con el tensor de curvatura de Riemann más general como

Rμ μ .. =Rα α μ μ α α .. .{displaystyle R_{munu }={R^{alpha {fnMi alpha nu},}

En el lado derecho, Tμ μ .. {displaystyle T... {munu}} es el tensor energético-momentum. Todos los tensores están escritos en notación de índice abstracto. Coincidiendo con la predicción de la teoría a los resultados observacionales para las órbitas planetarias o, equivalentemente, asegurando que el límite de baja gravedad débil y baja velocidad es la mecánica newtoniana, la constante proporcionalidad se encuentra 8π π Gc4{textstyle {frac {8cH00} G} {c^{4}}}, donde G{displaystyle G. es la constante gravitacional y c{displaystyle c} la velocidad de la luz en vacío. Cuando no hay ningún problema presente, de modo que el tensor energético-momentum desaparece, los resultados son las ecuaciones de vacío de Einstein,

Rμ μ .. =0.{displaystyle ¿Qué?

En relatividad general, la línea de universo de una partícula libre de toda fuerza externa no gravitatoria es un tipo particular de geodésica en el espacio-tiempo curvo. En otras palabras, una partícula que se mueve o cae libremente siempre se mueve a lo largo de una geodésica.

La ecuación geodésica es:

d2xμ μ ds2+.. μ μ α α β β dxα α dsdxβ β ds=0,{displaystyle {d^{2}x^{mu } over ds^{2}+ Gamma ^{mu {fnK} {fnMicrosoft Sans} {fnMicrosoft Sans} {fnMicrosoft Sans Serif}

Donde s{displaystyle s} es un parámetro escalar del movimiento (por ejemplo, el tiempo apropiado), y .. μ μ α α β β {displaystyle Gamma ^{mu }{alpha beta } son símbolos de Christoffel (a veces llamados coeficientes de conexión de afina o coeficientes de conexión Levi-Civita) que es simétrico en los dos índices inferiores. Los índices griegos pueden tomar los valores: 0, 1, 2, 3 y la convención de la suma se utiliza para índices repetidos α α {displaystyle alpha } y β β {displaystyle beta }. La cantidad en el lado izquierdo de esta ecuación es la aceleración de una partícula, y por lo tanto esta ecuación es análoga a las leyes de movimiento de Newton que también proporcionan fórmulas para la aceleración de una partícula. Esta ecuación de movimiento emplea la notación de Einstein, lo que significa que los índices repetidos se resumen (es decir, de cero a tres). Los símbolos de Christoffel son funciones de las cuatro coordenadas espacio-tiempo, y así son independientes de la velocidad o aceleración u otras características de una partícula de prueba cuyo movimiento es descrito por la ecuación geodésica.

Fuerza total en relatividad general

En relatividad general, la energía potencial gravitatoria efectiva de un objeto de masa m que gira alrededor de un cuerpo central masivo M viene dada por

Uf()r)=− − GMmr+L22mr2− − GML2mc2r3{displaystyle U_{f}(r)=-{frac {GMm} {r}+{frac} {fnK} {f} {f}}} {f}}} {f}} {f}}}}}}}}}

Entonces se puede obtener una fuerza total conservativa como

Ff()r)=− − GMmr2+L2mr3− − 3GML2mc2r4{displaystyle F_{f}(r)=-{frac {GMm}{2}}+{frac} {fnK} {f} {f}}} {f}}} {f}} {f}}}}} {f}}}}}}}} {f}}}}}}}} {f}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}

donde L es el momento angular. El primer término representa la fuerza de gravedad de Newton, que se describe mediante la ley del inverso del cuadrado. El segundo término representa la fuerza centrífuga en el movimiento circular. El tercer término representa el efecto relativista.

Alternativas a la relatividad general

Existen alternativas a la relatividad general basadas en las mismas premisas, que incluyen reglas y/o restricciones adicionales, lo que lleva a diferentes ecuaciones de campo. Algunos ejemplos son la teoría de Whitehead, la teoría de Brans-Dicke, el teleparalelismo, la gravedad f(R) y la teoría de Einstein-Cartan.

Definición y aplicaciones básicas

La derivación descrita en la sección anterior contiene toda la información necesaria para definir la relatividad general, describir sus propiedades clave y abordar una cuestión de importancia crucial en la física, a saber, cómo se puede utilizar la teoría para la construcción de modelos.

Definición y propiedades básicas

La relatividad general es una teoría métrica de la gravitación. En su núcleo se encuentran las ecuaciones de Einstein, que describen la relación entre la geometría de una variedad pseudo-Riemanniana de cuatro dimensiones que representa el espacio-tiempo y la energía-momentum contenida en ese espacio-tiempo. Los fenómenos que en la mecánica clásica se atribuyen a la acción de la fuerza de la gravedad (como la caída libre, el movimiento orbital y las trayectorias de las naves espaciales), corresponden al movimiento inercial dentro de una geometría curva del espacio-tiempo en relatividad general; no hay fuerza gravitatoria que desvíe los objetos de sus caminos rectos naturales. En cambio, la gravedad corresponde a cambios en las propiedades del espacio y el tiempo, lo que a su vez cambia los caminos más rectos posibles que seguirán los objetos de forma natural. La curvatura es, a su vez, causada por la energía-momento de la materia. Parafraseando al relativista John Archibald Wheeler, el espacio-tiempo le dice a la materia cómo moverse; la materia le dice al espacio-tiempo cómo curvarse.

Mientras que la relatividad general reemplaza el potencial gravitatorio escalar de la física clásica por un tensor simétrico de rango dos, este último se reduce al primero en ciertos casos límite. Para campos gravitatorios débiles y velocidades lentas en relación con la velocidad de la luz, las predicciones de la teoría convergen con las de la ley de gravitación universal de Newton.

Como se construye usando tensores, la relatividad general exhibe una covarianza general: sus leyes, y otras leyes formuladas dentro del marco de la relatividad general, toman la misma forma en todos los sistemas de coordenadas. Además, la teoría no contiene estructuras de fondo geométricas invariantes, es decir, es independiente del fondo. Por lo tanto, satisface un principio general más estricto de la relatividad, a saber, que las leyes de la física son las mismas para todos los observadores. Localmente, como se expresa en el principio de equivalencia, el espacio-tiempo es minkowskiano, y las leyes de la física exhiben invariancia local de Lorentz.

Construcción de modelos

El concepto central de la construcción de modelos relativistas generales es el de una solución de las ecuaciones de Einstein. Dadas las ecuaciones de Einstein y las ecuaciones adecuadas para las propiedades de la materia, dicha solución consiste en una variedad semirriemanniana específica (generalmente definida al dar la métrica en coordenadas específicas) y campos de materia específicos definidos en esa variedad. La materia y la geometría deben satisfacer las ecuaciones de Einstein, por lo que, en particular, el tensor de energía-momento de la materia debe estar libre de divergencias. Por supuesto, la materia también debe satisfacer las ecuaciones adicionales que se impongan a sus propiedades. En resumen, tal solución es un universo modelo que satisface las leyes de la relatividad general y, posiblemente, leyes adicionales que rigen cualquier materia que pueda estar presente.

Las ecuaciones de Einstein son ecuaciones diferenciales parciales no lineales y, como tales, difíciles de resolver con exactitud. Sin embargo, se conocen varias soluciones exactas, aunque solo unas pocas tienen aplicaciones físicas directas. Las soluciones exactas más conocidas, y también las más interesantes desde el punto de vista de la física, son la solución de Schwarzschild, la solución de Reissner-Nordström y la métrica de Kerr, cada una correspondiente a un cierto tipo de agujero negro en un universo vacío, y los universos de Friedmann-Lemaître-Robertson-Walker y de Sitter, cada uno de los cuales describe un cosmos en expansión. Las soluciones exactas de gran interés teórico incluyen el universo de Gödel (que abre la intrigante posibilidad de viajar en el tiempo en espacios-tiempo curvos), la solución de Taub-NUT (un universo modelo que es homogéneo, pero anisótropo) y el espacio anti-de Sitter (que ha llegado recientemente a la prominencia en el contexto de lo que se llama la conjetura de Maldacena).

Dada la dificultad de encontrar soluciones exactas, las ecuaciones de campo de Einstein también se resuelven con frecuencia mediante integración numérica en una computadora o considerando pequeñas perturbaciones de soluciones exactas. En el campo de la relatividad numérica, se emplean poderosas computadoras para simular la geometría del espacio-tiempo y resolver las ecuaciones de Einstein para situaciones interesantes, como dos agujeros negros en colisión. En principio, dichos métodos pueden aplicarse a cualquier sistema, dados los recursos informáticos suficientes, y pueden abordar cuestiones fundamentales como las singularidades desnudas. También se pueden encontrar soluciones aproximadas mediante teorías de perturbación como la gravedad linealizada y su generalización, la expansión posnewtoniana, ambas desarrolladas por Einstein. Este último proporciona un enfoque sistemático para resolver la geometría de un espacio-tiempo que contiene una distribución de materia que se mueve lentamente en comparación con la velocidad de la luz. La expansión involucra una serie de términos; los primeros términos representan la gravedad newtoniana, mientras que los términos posteriores representan correcciones cada vez más pequeñas a la teoría de Newton debido a la relatividad general. Una extensión de esta expansión es el formalismo posnewtoniano parametrizado (PPN), que permite comparaciones cuantitativas entre las predicciones de la relatividad general y las teorías alternativas.

Consecuencias de la teoría de Einstein

La relatividad general tiene una serie de consecuencias físicas. Algunos se derivan directamente de los axiomas de la teoría, mientras que otros se aclararon solo en el curso de muchos años de investigación que siguieron a la publicación inicial de Einstein.

Dilatación del tiempo gravitacional y cambio de frecuencia

Representación esquemática del rojizo gravitacional de una onda ligera que escapa de la superficie de un cuerpo masivo

Suponiendo que se cumple el principio de equivalencia, la gravedad influye en el paso del tiempo. La luz enviada hacia abajo en un pozo de gravedad se desplaza hacia el azul, mientras que la luz enviada en la dirección opuesta (es decir, saliendo del pozo de gravedad) se desplaza hacia el rojo; colectivamente, estos dos efectos se conocen como el cambio de frecuencia gravitacional. De manera más general, los procesos cercanos a un cuerpo masivo son más lentos en comparación con los procesos que tienen lugar más lejos; este efecto se conoce como dilatación del tiempo gravitacional.

El corrimiento al rojo gravitacional se ha medido en el laboratorio y mediante observaciones astronómicas. La dilatación del tiempo gravitatorio en el campo gravitatorio de la Tierra se ha medido numerosas veces utilizando relojes atómicos, mientras que la validación continua se proporciona como un efecto secundario de la operación del Sistema de Posicionamiento Global (GPS). La observación de púlsares binarios proporciona pruebas en campos gravitatorios más intensos. Todos los resultados están de acuerdo con la relatividad general. Sin embargo, con el nivel actual de precisión, estas observaciones no pueden distinguir entre la relatividad general y otras teorías en las que el principio de equivalencia es válido.

Desviación de la luz y retardo de tiempo gravitatorio

Deflexión de la luz (sentado fuera de la ubicación mostrada en azul) cerca de un cuerpo compacto (shown in gray)

La relatividad general predice que la trayectoria de la luz seguirá la curvatura del espacio-tiempo cuando pase cerca de una estrella. Este efecto se confirmó inicialmente al observar que la luz de las estrellas o de los cuásares distantes se desvía cuando pasa junto al Sol.

Esta predicción y otras relacionadas se derivan del hecho de que la luz sigue lo que se denomina una geodésica similar a la luz o nula, una generalización de las líneas rectas a lo largo de las cuales viaja la luz en la física clásica. Tales geodésicas son la generalización de la invariancia de la velocidad de la luz en la relatividad especial. A medida que se examinan modelos de espacio-tiempo adecuados (ya sea la solución exterior de Schwarzschild o, para más de una sola masa, la expansión posnewtoniana), surgen varios efectos de la gravedad sobre la propagación de la luz. Aunque la curvatura de la luz también se puede derivar extendiendo la universalidad de la caída libre a la luz, el ángulo de deflexión resultante de tales cálculos es solo la mitad del valor dado por la relatividad general.

Estrechamente relacionado con la deflexión de la luz está el retraso de tiempo gravitacional (o retraso de Shapiro), el fenómeno por el cual las señales de luz tardan más en moverse a través de un campo gravitacional de lo que lo harían en ausencia de ese campo. Ha habido numerosas pruebas exitosas de esta predicción. En el formalismo posnewtoniano parametrizado (PPN), las mediciones tanto de la desviación de la luz como del retardo gravitatorio determinan un parámetro llamado γ, que codifica la influencia de la gravedad en la geometría del espacio.

Ondas gravitacionales

Anillo de partículas de prueba deformadas por un paso (linearizado, amplificado para una mejor visibilidad) onda gravitacional

Predichas en 1916 por Albert Einstein, existen ondas gravitacionales: ondas en la métrica del espacio-tiempo que se propagan a la velocidad de la luz. Estas son una de varias analogías entre la gravedad de campo débil y el electromagnetismo en el sentido de que son análogas a las ondas electromagnéticas. El 11 de febrero de 2016, el equipo de Advanced LIGO anunció que había detectado directamente ondas gravitacionales de la fusión de un par de agujeros negros.

El tipo más simple de tal onda puede ser visualizado por su acción en un anillo de partículas libremente flotantes. Una onda sine propagando a través de tal anillo hacia el lector distorsiona el anillo de forma característica y rítmica (imagen animada a la derecha). Dado que las ecuaciones de Einstein son ondas gravitacionales no lineales, arbitrariamente fuertes no obedecen la superposición lineal, dificultando su descripción. Sin embargo, las aproximaciones lineales de las ondas gravitacionales son suficientemente precisas para describir las ondas extremadamente débiles que se espera que lleguen aquí en la Tierra desde acontecimientos cósmicos lejanos, lo que generalmente resulta en distancias relativas aumentando y disminuyendo al aumentar 10− − 21{displaystyle 10^{-21} o menos. Los métodos de análisis de datos suelen hacer uso del hecho de que estas ondas linearizadas pueden ser descompuestas Fourier.

Algunas soluciones exactas describen ondas gravitacionales sin ninguna aproximación, por ejemplo, un tren de ondas que viaja a través del espacio vacío o universos Gowdy, variedades de un cosmos en expansión lleno de ondas gravitacionales. Pero para las ondas gravitacionales producidas en situaciones astrofísicamente relevantes, como la fusión de dos agujeros negros, los métodos numéricos son actualmente la única forma de construir modelos apropiados.

Efectos orbitales y la relatividad de la dirección

La relatividad general difiere de la mecánica clásica en una serie de predicciones relativas a los cuerpos en órbita. Predice una rotación general (precesión) de las órbitas planetarias, así como el decaimiento orbital causado por la emisión de ondas gravitacionales y efectos relacionados con la relatividad de la dirección.

Precesión de ábsides

Newtonian (red) vs. Einsteinian orbit (blue) de un planeta solitario orbitando una estrella. La influencia de otros planetas es ignorada.

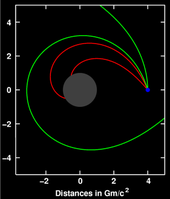
En la relatividad general, los ábsides de cualquier órbita (el punto de máxima aproximación del cuerpo en órbita al centro de masa del sistema) sufrirán una precesión; la órbita no es una elipse, sino similar a una elipse que gira sobre su foco, lo que da como resultado una forma de curva de rosa (ver imagen). Einstein primero derivó este resultado utilizando una métrica aproximada que representaba el límite newtoniano y tratando el cuerpo en órbita como una partícula de prueba. Para él, el hecho de que su teoría diera una explicación directa del desplazamiento anómalo del perihelio de Mercurio, descubierto anteriormente por Urbain Le Verrier en 1859, era una prueba importante de que por fin había identificado la forma correcta de las ecuaciones del campo gravitatorio.

El efecto también se puede derivar utilizando la métrica exacta de Schwarzschild (que describe el espacio-tiempo alrededor de una masa esférica) o el formalismo posnewtoniano mucho más general. Se debe a la influencia de la gravedad en la geometría del espacio y a la contribución de la energía propia a la gravedad de un cuerpo (codificada en la no linealidad de las ecuaciones de Einstein). La precesión relativista se ha observado en todos los planetas que permiten mediciones de precesión precisas (Mercurio, Venus y la Tierra), así como en los sistemas de púlsares binarios, donde es mayor en cinco órdenes de magnitud.

En la relatividad general el cambio de perihelio σ σ {displaystyle sigma }, expresado en radianos por revolución, es dado aproximadamente por

σ σ =24π π 3L2T2c2()1− − e2),{displaystyle sigma ={frac {24pi ¿Qué?

donde:

• L{displaystyle L. es el eje semi-major
• T{displaystyle T} es el período orbital
• c{displaystyle c} es la velocidad de la luz en vacío
• e{displaystyle e} es la excentricidad orbital

Desintegración orbital

Decaimiento orbital para PSR 1913+16: cambio de tiempo (en s), rastreado más de 30 años (2006).

Decaimiento orbital para PSR J0737−3039: cambio de tiempo (en s), seguimiento de más de 16 años (2021).

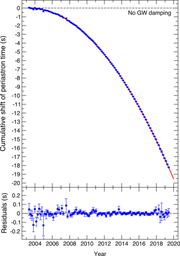
Según la relatividad general, un sistema binario emitirá ondas gravitacionales y, por lo tanto, perderá energía. Debido a esta pérdida, la distancia entre los dos cuerpos en órbita disminuye, al igual que su período orbital. Dentro del Sistema Solar o para estrellas dobles ordinarias, el efecto es demasiado pequeño para ser observable. Este no es el caso de un púlsar binario cercano, un sistema de dos estrellas de neutrones en órbita, una de las cuales es un púlsar: desde el púlsar, los observadores en la Tierra reciben una serie regular de pulsos de radio que pueden servir como un reloj de alta precisión, que permite mediciones precisas del período orbital. Debido a que las estrellas de neutrones son inmensamente compactas, se emiten cantidades significativas de energía en forma de radiación gravitatoria.

La primera observación de una disminución en el período orbital debido a la emisión de ondas gravitacionales fue realizada por Hulse y Taylor, utilizando el púlsar binario PSR1913+16 que habían descubierto en 1974. Esta fue la primera detección de ondas gravitacionales, aunque indirectas., por la que fueron galardonados con el Premio Nobel de Física de 1993. Desde entonces, se han encontrado varios otros púlsares binarios, en particular el púlsar doble PSR J0737−3039, donde ambas estrellas son púlsares y que se informó por última vez que también estaba de acuerdo con la relatividad general en 2021 después de 16 años de observaciones.

Precesión geodésica y arrastre de marcos

Varios efectos relativistas están directamente relacionados con la relatividad de la dirección. Una es la precesión geodésica: la dirección del eje de un giroscopio en caída libre en un espacio-tiempo curvo cambiará cuando se compara, por ejemplo, con la dirección de la luz recibida de estrellas distantes, aunque tal giroscopio representa la forma de mantener una dirección tan estable como sea posible. posible ("transporte paralelo"). Para el sistema Luna-Tierra, este efecto se ha medido con la ayuda del alcance del láser lunar. Más recientemente, se ha medido para masas de prueba a bordo del satélite Gravity Probe B con una precisión superior al 0,3 %.

Cerca de una masa giratoria, hay efectos gravitomagnéticos o de arrastre de marcos. Un observador distante determinará que los objetos cercanos a la masa son "arrastrados". Esto es más extremo para los agujeros negros giratorios donde, para cualquier objeto que entre en una zona conocida como ergosfera, la rotación es inevitable. Dichos efectos pueden probarse nuevamente a través de su influencia en la orientación de los giroscopios en caída libre. Se han realizado pruebas algo controvertidas utilizando los satélites LAGEOS, lo que confirma la predicción relativista. También se ha utilizado la sonda Mars Global Surveyor alrededor de Marte.

Interpretaciones

Interpretación Neo-Lorentziana

Franco Selleri y Antony Valentini son ejemplos de físicos destacados que apoyan las explicaciones neolorentzianas de la relatividad general.

Aplicaciones astrofísicas

Lentes gravitacionales

Cruz de Einstein: cuatro imágenes del mismo objeto astronómico, producidas por un lente gravitacional

La desviación de la luz por la gravedad es responsable de una nueva clase de fenómenos astronómicos. Si un objeto masivo está situado entre el astrónomo y un objeto distante con masa y distancias relativas apropiadas, el astrónomo verá múltiples imágenes distorsionadas del objetivo. Estos efectos se conocen como lentes gravitacionales. Según la configuración, la escala y la distribución de masa, puede haber dos o más imágenes, un anillo brillante conocido como anillo de Einstein o anillos parciales llamados arcos. El primer ejemplo se descubrió en 1979; desde entonces, se han observado más de cien lentes gravitacionales. Incluso si las múltiples imágenes están demasiado cerca unas de otras para ser resueltas, el efecto aún se puede medir, por ejemplo, como un brillo general del objeto de destino; una serie de tales "eventos de microlente" han sido observados.

Las lentes gravitacionales se han convertido en una herramienta de observación astronómica. Se utiliza para detectar la presencia y distribución de materia oscura, proporcionar un "telescopio natural" para observar galaxias distantes y obtener una estimación independiente de la constante de Hubble. Las evaluaciones estadísticas de los datos de lentes proporcionan información valiosa sobre la evolución estructural de las galaxias.

Astronomía de ondas gravitacionales

La impresión del artista del detector de ondas gravitacionales de origen espacial LISA

Las observaciones de púlsares binarios proporcionan una fuerte evidencia indirecta de la existencia de ondas gravitacionales (ver Decaimiento orbital, arriba). La detección de estas ondas es un objetivo principal de la investigación actual relacionada con la relatividad. Actualmente se encuentran en funcionamiento varios detectores de ondas gravitacionales terrestres, entre los que destacan los detectores interferométricos GEO 600, LIGO (dos detectores), TAMA 300 y VIRGO. Varias matrices de sincronización de púlsares utilizan púlsares de milisegundos para detectar ondas gravitacionales en el rango de frecuencia de 10⁻⁹ a 10⁻⁶ hercios, que se originan en agujeros negros supermasivos binarios. Actualmente se está desarrollando un detector europeo basado en el espacio, eLISA / NGO, con una misión precursora (LISA Pathfinder) lanzada en diciembre de 2015.

Las observaciones de ondas gravitacionales prometen complementar las observaciones en el espectro electromagnético. Se espera que proporcionen información sobre agujeros negros y otros objetos densos como estrellas de neutrones y enanas blancas, sobre ciertos tipos de implosiones de supernovas y sobre procesos en el universo muy primitivo, incluida la firma de ciertos tipos de cuerdas cósmicas hipotéticas. En febrero de 2016, el equipo de Advanced LIGO anunció que había detectado ondas gravitacionales de una fusión de agujeros negros.

Agujeros negros y otros objetos compactos

Simulación basada en las ecuaciones de la relatividad general: una estrella colapsando para formar un agujero negro mientras emite ondas gravitacionales

Siempre que la relación entre la masa de un objeto y su radio se vuelve lo suficientemente grande, la relatividad general predice la formación de un agujero negro, una región del espacio de la que nada, ni siquiera la luz, puede escapar. En los modelos actualmente aceptados de evolución estelar, se cree que las estrellas de neutrones de alrededor de 1,4 masas solares y los agujeros negros estelares con unas pocas a unas pocas docenas de masas solares son el estado final para la evolución de estrellas masivas. Por lo general, una galaxia tiene un agujero negro supermasivo con unos pocos millones a unos pocos miles de millones de masas solares en su centro, y se cree que su presencia desempeñó un papel importante en la formación de la galaxia y estructuras cósmicas más grandes.

Astronómicamente, la propiedad más importante de los objetos compactos es que proporcionan un mecanismo extremadamente eficiente para convertir la energía gravitacional en radiación electromagnética. Se cree que la acreción, la caída de polvo o materia gaseosa sobre agujeros negros estelares o supermasivos, es responsable de algunos objetos astronómicos espectacularmente luminosos, en particular diversos tipos de núcleos galácticos activos en escalas galácticas y objetos de tamaño estelar como los microquásares. En particular, la acumulación puede conducir a chorros relativistas, haces enfocados de partículas altamente energéticas que se lanzan al espacio casi a la velocidad de la luz. La relatividad general juega un papel central en el modelado de todos estos fenómenos, y las observaciones proporcionan una fuerte evidencia de la existencia de agujeros negros con las propiedades predichas por la teoría.

Los agujeros negros también son objetivos buscados en la búsqueda de ondas gravitacionales (cf. Ondas gravitacionales, arriba). La fusión de binarios de agujeros negros debería llevar a que algunas de las señales de ondas gravitacionales más fuertes lleguen a los detectores aquí en la Tierra, y la fase inmediatamente anterior a la fusión ("chirrido") podría usarse como una "vela estándar"; para deducir la distancia a los eventos de fusión y, por lo tanto, servir como una prueba de expansión cósmica a grandes distancias. Las ondas gravitacionales producidas cuando un agujero negro estelar se sumerge en uno supermasivo deberían proporcionar información directa sobre la geometría del agujero negro supermasivo.

Cosmología

Esta herradura azul es una galaxia lejana que ha sido magnificada y convertida en un anillo casi completo por la fuerte atracción gravitacional de la enorme galaxia roja luminosa de primer plano.

Los modelos actuales de cosmología se basan en las ecuaciones de campo de Einstein, que incluyen la constante cosmológica ▪ ▪ {displaystyle Lambda } ya que tiene una influencia importante en la dinámica a gran escala del cosmos,

Rμ μ .. − − 12Rgμ μ .. +▪ ▪ gμ μ .. =8π π Gc4Tμ μ .. {displaystyle R_{munu }-{textstyle 1 over 2}R,g_{munu }+Lambda g_{munu }={frac {8pi G} {c^{4}, T... {munu}}

Donde gμ μ .. {displaystyle g_{munu}} es la métrica espacial. Las soluciones isotrópicas y homogéneas de estas ecuaciones mejoradas, las soluciones Friedmann-Lemaître-Robertson-Walker, permiten a los físicos modelar un universo que ha evolucionado durante los últimos 14 mil millones de años desde una fase de Big Bang caliente y temprana. Una vez que un pequeño número de parámetros (por ejemplo, la densidad de materia media del universo) se han fijado por observación astronómica, se pueden utilizar más datos observacionales para poner los modelos a prueba. Las predicciones, todas exitosas, incluyen la abundancia inicial de elementos químicos formados en un período de nucleosíntesis primordial, la estructura a gran escala del universo, y la existencia y propiedades de un " eco térmico" del cosmos temprano, la radiación de fondo cósmico.

Las observaciones astronómicas de la tasa de expansión cosmológica permiten estimar la cantidad total de materia en el universo, aunque la naturaleza de esa materia sigue siendo un misterio en parte. Alrededor del 90% de toda la materia parece ser materia oscura, que tiene masa (o, de manera equivalente, influencia gravitacional), pero no interactúa electromagnéticamente y, por lo tanto, no se puede observar directamente. No existe una descripción generalmente aceptada de este nuevo tipo de materia, dentro del marco de la física de partículas conocida o de otro tipo. La evidencia observacional de los estudios de desplazamiento al rojo de supernovas distantes y las mediciones de la radiación de fondo cósmica también muestran que la evolución de nuestro universo está significativamente influenciada por una constante cosmológica que resulta en una aceleración de la expansión cósmica o, de manera equivalente, por una forma de energía con una ecuación inusual. de estado, conocida como energía oscura, cuya naturaleza sigue sin estar clara.

En 1980 se planteó la hipótesis de una fase inflacionaria, una fase adicional de expansión fuertemente acelerada en tiempos cósmicos de alrededor de 10⁻³³ segundos, para explicar varias observaciones desconcertantes que no estaban explicadas por los modelos cosmológicos clásicos, como como la homogeneidad casi perfecta de la radiación cósmica de fondo. Las mediciones recientes de la radiación cósmica de fondo han dado como resultado la primera evidencia de este escenario. Sin embargo, existe una variedad desconcertante de posibles escenarios inflacionarios, que no pueden ser restringidos por las observaciones actuales. Una pregunta aún mayor es la física del universo más primitivo, antes de la fase inflacionaria y cerca de donde los modelos clásicos predicen la singularidad del big bang. Una respuesta autorizada requeriría una teoría completa de la gravedad cuántica, que aún no se ha desarrollado (cf. la sección sobre la gravedad cuántica, a continuación).

Soluciones exóticas: viajes en el tiempo, motores warp

Kurt Gödel demostró que existen soluciones para las ecuaciones de Einstein que contienen curvas temporales cerradas (CTC), que permiten bucles en el tiempo. Las soluciones requieren condiciones físicas extremas que es poco probable que ocurran en la práctica, y sigue siendo una pregunta abierta si otras leyes de la física las eliminarán por completo. Desde entonces, se han encontrado otras soluciones GR que contienen CTC, igualmente poco prácticas, como el cilindro Tipler y los agujeros de gusano transitables. Stephen Hawking introdujo la conjetura de protección de la cronología, que es una suposición más allá de las de la relatividad general estándar para evitar los viajes en el tiempo.

Algunas soluciones exactas en relatividad general, como la impulsión de Alcubierre, presentan ejemplos de impulsión warp, pero estas soluciones requieren una distribución de materia exótica y, en general, sufren de inestabilidad semiclásica.

Conceptos avanzados

Simetrías asintóticas

El grupo de simetría del espacio-tiempo para la relatividad especial es el grupo de Poincaré, que es un grupo de diez dimensiones de tres impulsos de Lorentz, tres rotaciones y cuatro traslaciones del espacio-tiempo. Es lógico preguntar qué simetrías, si es que hay alguna, podrían aplicarse en la relatividad general. Un caso manejable podría ser considerar las simetrías del espacio-tiempo tal como las ven los observadores ubicados lejos de todas las fuentes del campo gravitatorio. La expectativa ingenua de las simetrías del espacio-tiempo asintóticamente planas podría ser simplemente extender y reproducir las simetrías del espacio-tiempo plano de la relatividad especial, a saber, el grupo de Poincaré.

En 1962, Hermann Bondi, M. G. van der Burg, A. W. Metzner y Rainer K. Sachs abordaron este problema de simetría asintótica para investigar el flujo de energía en el infinito debido a la propagación de ondas gravitacionales. Su primer paso fue decidir sobre algunas condiciones de contorno físicamente sensibles para colocar en el campo gravitacional en el infinito similar a la luz para caracterizar lo que significa decir que una métrica es asintóticamente plana, sin hacer suposiciones a priori sobre el naturaleza del grupo de simetría asintótica, ni siquiera la suposición de que tal grupo existe. Luego, después de diseñar lo que consideraban las condiciones de contorno más sensibles, investigaron la naturaleza de las transformaciones de simetría asintótica resultantes que dejan invariable la forma de las condiciones de contorno apropiadas para campos gravitatorios asintóticamente planos. Lo que encontraron fue que las transformaciones de simetría asintótica en realidad forman un grupo y la estructura de este grupo no depende del campo gravitacional particular que esté presente. Esto significa que, como era de esperar, se puede separar la cinemática del espacio-tiempo de la dinámica del campo gravitatorio al menos en el infinito espacial. La desconcertante sorpresa en 1962 fue su descubrimiento de un rico grupo de dimensión infinita (el llamado grupo BMS) como grupo de simetría asintótica, en lugar del grupo de Poincaré de dimensión finita, que es un subgrupo del grupo BMS. Las transformaciones de Lorentz no solo son transformaciones de simetría asintótica, también hay transformaciones adicionales que no son transformaciones de Lorentz sino transformaciones de simetría asintótica. De hecho, encontraron una infinidad adicional de generadores de transformación conocidos como supertraducciones. Esto implica la conclusión de que la Relatividad General (GR) no se reduce a la relatividad especial en el caso de campos débiles a largas distancias. Resulta que la simetría BMS, convenientemente modificada, podría verse como una reafirmación del teorema universal del gravitón suave en la teoría cuántica de campos (QFT), que relaciona el QFT infrarrojo universal (suave) con las simetrías asintóticas del espacio-tiempo GR.

Estructura causal y geometría global

Penrose–Carter diagrama de un universo infinito de Minkowski

En la relatividad general, ningún cuerpo material puede alcanzar o superar un pulso de luz. Ninguna influencia de un evento A puede llegar a ninguna otra ubicación X antes de que la luz se envíe de A a X. En consecuencia, una exploración de todas las líneas de mundo de luz (geodésicas nulas) arroja información clave sobre la estructura causal del espacio-tiempo. Esta estructura se puede mostrar utilizando diagramas de Penrose-Carter en los que regiones infinitamente grandes del espacio e infinitos intervalos de tiempo se contraen ('compactan') para encajar en un mapa finito, mientras que la luz todavía viaja a lo largo de las diagonales como en diagramas estándar de espacio-tiempo.

Conscientes de la importancia de la estructura causal, Roger Penrose y otros desarrollaron lo que se conoce como geometría global. En geometría global, el objeto de estudio no es una solución particular (o familia de soluciones) a las ecuaciones de Einstein. Más bien, las relaciones que son válidas para todas las geodésicas, como la ecuación de Raychaudhuri, y suposiciones adicionales no específicas sobre la naturaleza de la materia (generalmente en forma de condiciones de energía) se utilizan para obtener resultados generales.

Horizontes

Usando la geometría global, se puede mostrar que algunos espaciotiempos contienen límites llamados horizontes, que delimitan una región del resto del espaciotiempo. Los ejemplos más conocidos son los agujeros negros: si la masa se comprime en una región del espacio suficientemente compacta (como se especifica en la conjetura del aro, la escala de longitud relevante es el radio de Schwarzschild), ninguna luz del interior puede escapar al exterior. Dado que ningún objeto puede superar un pulso de luz, toda la materia interior también queda aprisionada. El paso del exterior al interior todavía es posible, lo que demuestra que el límite, el horizonte del agujero negro, no es una barrera física.

La ergósfera de un agujero negro giratorio, que juega un papel clave cuando se trata de extraer energía de tal agujero negro

Los primeros estudios de los agujeros negros se basaban en soluciones explícitas de las ecuaciones de Einstein, en particular, la solución de Schwarzschild con simetría esférica (utilizada para describir un agujero negro estático) y la solución de Kerr axisimétrica (utilizada para describir un agujero negro estacionario y giratorio)., e introduciendo características interesantes como la ergosfera). Usando geometría global, estudios posteriores han revelado propiedades más generales de los agujeros negros. Con el tiempo se convierten en objetos bastante simples caracterizados por once parámetros que especifican: carga eléctrica, masa-energía, momento lineal, momento angular y ubicación en un momento específico. Esto lo afirma el teorema de unicidad de los agujeros negros: 'los agujeros negros no tienen cabello', es decir, no tienen marcas distintivas como los peinados de los humanos. Independientemente de la complejidad de un objeto gravitatorio que colapsa para formar un agujero negro, el objeto que resulta (habiendo emitido ondas gravitacionales) es muy simple.

Aún más notable, existe un conjunto general de leyes conocidas como mecánica de agujeros negros, que es análoga a las leyes de la termodinámica. Por ejemplo, según la segunda ley de la mecánica de los agujeros negros, el área del horizonte de sucesos de un agujero negro general nunca disminuirá con el tiempo, de forma análoga a la entropía de un sistema termodinámico. Esto limita la energía que se puede extraer por medios clásicos de un agujero negro en rotación (por ejemplo, mediante el proceso de Penrose). Existe una fuerte evidencia de que las leyes de la mecánica de los agujeros negros son, de hecho, un subconjunto de las leyes de la termodinámica, y que el área del agujero negro es proporcional a su entropía. Esto conduce a una modificación de las leyes originales de la mecánica de los agujeros negros: por ejemplo, a medida que la segunda ley de la mecánica de los agujeros negros se convierte en parte de la segunda ley de la termodinámica, es posible que el área de los agujeros negros disminuya, siempre que otros procesos lo aseguren. que, en conjunto, la entropía aumenta. Como objetos termodinámicos con temperatura distinta de cero, los agujeros negros deberían emitir radiación térmica. Los cálculos semiclásicos indican que efectivamente lo hacen, con la gravedad de la superficie desempeñando el papel de la temperatura en la ley de Planck. Esta radiación se conoce como radiación de Hawking (cf. la sección de teoría cuántica, a continuación).

Hay otros tipos de horizontes. En un universo en expansión, un observador puede encontrar que algunas regiones del pasado no se pueden observar ("horizonte de partículas"), y algunas regiones del futuro no se pueden influenciar (horizonte de eventos). Incluso en el espacio plano de Minkowski, cuando lo describe un observador acelerado (espacio de Rindler), habrá horizontes asociados con una radiación semiclásica conocida como radiación Unruh.

Singularidades

Otra característica general de la relatividad general es la aparición de límites de espacio-tiempo conocidos como singularidades. El espacio-tiempo se puede explorar siguiendo las geodésicas similares al tiempo y a la luz, todas las formas posibles en que la luz y las partículas en caída libre pueden viajar. Pero algunas soluciones de las ecuaciones de Einstein tienen "bordes irregulares", regiones conocidas como singularidades del espacio-tiempo, donde los caminos de la luz y las partículas que caen llegan a un final abrupto y la geometría se vuelve mal definida. En los casos más interesantes, se trata de "singularidades de curvatura", donde las cantidades geométricas que caracterizan la curvatura del espacio-tiempo, como el escalar de Ricci, toman valores infinitos. Ejemplos bien conocidos de espaciotiempos con singularidades futuras, donde terminan las líneas de tiempo, son la solución de Schwarzschild, que describe una singularidad dentro de un agujero negro estático eterno, o la solución de Kerr con su singularidad en forma de anillo dentro de un agujero negro giratorio eterno. Las soluciones de Friedmann-Lemaître-Robertson-Walker y otros espaciotiempos que describen universos tienen singularidades pasadas en las que comienzan las líneas de mundo, a saber, singularidades del Big Bang, y algunas también tienen singularidades futuras (Big Crunch).

Dado que estos ejemplos son todos muy simétricos, y por lo tanto simplificados, es tentador concluir que la aparición de singularidades es un artefacto de idealización. Los famosos teoremas de singularidad, probados utilizando los métodos de la geometría global, dicen lo contrario: las singularidades son una característica genérica de la relatividad general, e inevitables una vez que el colapso de un objeto con propiedades materiales realistas ha superado cierta etapa y también al comienzo de una amplia clase de universos en expansión. Sin embargo, los teoremas dicen poco sobre las propiedades de las singularidades y gran parte de la investigación actual se dedica a caracterizar estas entidades. estructura genérica (hipotetizada, por ejemplo, por la conjetura BKL). La hipótesis de la censura cósmica establece que todas las singularidades futuras realistas (sin simetrías perfectas, materia con propiedades realistas) están ocultas de forma segura detrás de un horizonte y, por lo tanto, invisibles para todos los observadores distantes. Si bien aún no existe una prueba formal, las simulaciones numéricas ofrecen evidencia de respaldo de su validez.

Ecuaciones de evolución

Cada solución de la ecuación de Einstein abarca toda la historia de un universo; no es solo una instantánea de cómo son las cosas, sino un espacio-tiempo completo, posiblemente lleno de materia. Describe el estado de la materia y la geometría en todas partes y en cada momento en ese universo en particular. Debido a su covarianza general, la teoría de Einstein no es suficiente por sí sola para determinar la evolución temporal del tensor métrico. Debe combinarse con una condición de coordenadas, que es análoga a la fijación de indicadores en otras teorías de campo.

Para entender las ecuaciones de Einstein como ecuaciones diferenciales parciales, es útil formularlas de una manera que describa la evolución del universo a lo largo del tiempo. Esto se hace en "3+1" formulaciones, donde el espacio-tiempo se divide en tres dimensiones espaciales y una dimensión temporal. El ejemplo más conocido es el formalismo ADM. Estas descomposiciones muestran que las ecuaciones de evolución del espacio-tiempo de la relatividad general se comportan bien: las soluciones siempre existen y se definen de forma única, una vez que se han especificado las condiciones iniciales adecuadas. Tales formulaciones de las ecuaciones de campo de Einstein son la base de la relatividad numérica.

Cantidades globales y casi locales

La noción de ecuaciones de evolución está íntimamente ligada a otro aspecto de la física relativista general. En la teoría de Einstein, resulta imposible encontrar una definición general para una propiedad aparentemente simple como la masa (o energía) total de un sistema. La razón principal es que al campo gravitatorio, como a cualquier campo físico, se le debe atribuir cierta energía, pero resulta fundamentalmente imposible localizar esa energía.

Sin embargo, hay posibilidades de definir la masa total de un sistema, ya sea usando un hipotético "observador infinitamente distante" (masa ADM) o simetrías adecuadas (masa Komar). Si se excluye de la masa total del sistema la energía que las ondas gravitacionales llevan al infinito, el resultado es la masa de Bondi en el infinito nulo. Al igual que en la física clásica, se puede demostrar que estas masas son positivas. Existen definiciones globales correspondientes para el momento y el momento angular. También ha habido varios intentos de definir cantidades cuasi-locales, como la masa de un sistema aislado formulado usando solo cantidades definidas dentro de una región finita del espacio que contiene ese sistema. La esperanza es obtener una cantidad útil para declaraciones generales sobre sistemas aislados, como una formulación más precisa de la conjetura del aro.

Relación con la teoría cuántica

Si se considerara que la relatividad general es uno de los dos pilares de la física moderna, entonces la teoría cuántica, la base para comprender la materia desde las partículas elementales hasta la física del estado sólido, sería el otro. Sin embargo, cómo reconciliar la teoría cuántica con la relatividad general sigue siendo una pregunta abierta.

Teoría cuántica de campos en espacio-tiempo curvo

Las teorías de campo cuántico ordinarias, que forman la base de la física de partículas elementales moderna, se definen en el espacio plano de Minkowski, que es una excelente aproximación cuando se trata de describir el comportamiento de partículas microscópicas en campos gravitatorios débiles como los que se encuentran en la Tierra. Para describir situaciones en las que la gravedad es lo suficientemente fuerte como para influir en la materia (cuántica), pero no lo suficientemente fuerte como para requerir la propia cuantización, los físicos han formulado teorías cuánticas de campo en el espacio-tiempo curvo. Estas teorías se basan en la relatividad general para describir un espacio-tiempo de fondo curvo y definen una teoría de campo cuántico generalizada para describir el comportamiento de la materia cuántica dentro de ese espacio-tiempo. Usando este formalismo, se puede demostrar que los agujeros negros emiten un espectro de partículas de cuerpo negro conocido como radiación de Hawking, lo que lleva a la posibilidad de que se evaporen con el tiempo. Como se mencionó brevemente anteriormente, esta radiación juega un papel importante para la termodinámica de los agujeros negros.

Gravedad cuántica

La demanda de consistencia entre una descripción cuántica de la materia y una descripción geométrica del espacio-tiempo, así como la aparición de singularidades (donde las escalas de longitud de curvatura se vuelven microscópicas), indican la necesidad de una teoría completa de la gravedad cuántica: para una adecuada descripción del interior de los agujeros negros y del universo muy primitivo, se requiere una teoría en la que la gravedad y la geometría asociada del espacio-tiempo se describan en el lenguaje de la física cuántica. A pesar de los grandes esfuerzos, actualmente no se conoce ninguna teoría completa y consistente de la gravedad cuántica, aunque existen varios candidatos prometedores.

Proyección de un manifold de Calabi-Yau, una de las formas de compactar las dimensiones adicionales posited por la teoría de cuerdas

Los intentos de generalizar las teorías cuánticas de campo ordinarias, utilizadas en la física de partículas elementales para describir las interacciones fundamentales, para incluir la gravedad, han dado lugar a problemas graves. Algunos han argumentado que a bajas energías, este enfoque resulta exitoso, ya que da como resultado una teoría de gravedad de campo efectiva (cuántica) aceptable. Sin embargo, a energías muy altas, los resultados perturbadores son muy divergentes y conducen a modelos desprovistos de poder predictivo ("no renormalizabilidad perturbativa").

Red de giro simple del tipo utilizado en gravedad cuántica de bucle

Un intento de superar estas limitaciones es la teoría de cuerdas, una teoría cuántica no de partículas puntuales, sino de diminutos objetos unidimensionales extensos. La teoría promete ser una descripción unificada de todas las partículas e interacciones, incluida la gravedad; el precio a pagar son características inusuales como seis dimensiones adicionales de espacio además de las tres habituales. En lo que se conoce como la segunda revolución de supercuerdas, se conjeturó que tanto la teoría de cuerdas como una unificación de la relatividad general y la supersimetría conocida como supergravedad forman parte de un modelo hipotético de once dimensiones conocido como teoría M, que constituiría un modelo consistente y definido de manera única. teoría de la gravedad cuántica.

Otro enfoque comienza con los procedimientos de cuantificación canónica de la teoría cuántica. Usando la formulación de valor inicial de la relatividad general (cf. ecuaciones de evolución anteriores), el resultado es la ecuación de Wheeler-deWitt (un análogo de la ecuación de Schrödinger) que, lamentablemente, resulta estar mal definida sin un ultravioleta adecuado (celosía) corte. Sin embargo, con la introducción de lo que ahora se conoce como variables Ashtekar, esto conduce a un modelo prometedor conocido como gravedad cuántica de bucles. El espacio está representado por una estructura similar a una red llamada red de espín, que evoluciona con el tiempo en pasos discretos.

Dependiendo de qué características de la relatividad general y la teoría cuántica se acepten sin cambios, y en qué nivel se introduzcan los cambios, existen muchos otros intentos de llegar a una teoría viable de la gravedad cuántica, algunos ejemplos son la teoría reticular de la gravedad basada en el enfoque Feynman Path Integral y el cálculo Regge, triangulaciones dinámicas, conjuntos causales, modelos twistor o los modelos basados en integrales de trayectoria de la cosmología cuántica.

Todas las teorías candidatas aún tienen importantes problemas formales y conceptuales que superar. También se enfrentan al problema común de que, hasta el momento, no hay forma de someter a pruebas experimentales las predicciones de la gravedad cuántica (y, por lo tanto, decidir entre los candidatos dónde varían sus predicciones), aunque existe la esperanza de que esto cambie a medida que los datos futuros de cosmología. observaciones y experimentos de física de partículas se vuelve disponible.

Estado actual

Observación de ondas gravitacionales de la fusión de agujeros negros binarios GW150914

La relatividad general se ha convertido en un modelo muy exitoso de gravitación y cosmología, que hasta ahora ha superado muchas pruebas experimentales y de observación inequívocas. Sin embargo, hay fuertes indicios de que la teoría es incompleta. El problema de la gravedad cuántica y la cuestión de la realidad de las singularidades del espacio-tiempo siguen abiertas. Los datos de observación que se toman como evidencia de energía oscura y materia oscura podrían indicar la necesidad de una nueva física. Incluso tomada tal cual, la relatividad general es rica en posibilidades para una mayor exploración. Los relativistas matemáticos buscan comprender la naturaleza de las singularidades y las propiedades fundamentales de las ecuaciones de Einstein, mientras que los relativistas numéricos ejecutan simulaciones informáticas cada vez más potentes (como las que describen la fusión de agujeros negros). En febrero de 2016, se anunció que el equipo de Advanced LIGO detectó directamente la existencia de ondas gravitacionales el 14 de septiembre de 2015. Un siglo después de su introducción, la relatividad general sigue siendo un área de investigación muy activa.