Relación simétrica

ImprimirCitar

Tipo de relación binaria

Relaciones binarias transitivas

	Simétrico	Antisymmetric	Conectado	Bien fundada	Has joineds	Has meets	Reflexivo	Irreflexivo	Asimétrica
			Total, Semiconnex					Anti- reflexivo
Equivalencia relación	Y	✗	✗	✗	✗	✗	Y	✗	✗
Preorden (Quasiorder)	✗	✗	✗	✗	✗	✗	Y	✗	✗
Orden parcial	✗	Y	✗	✗	✗	✗	Y	✗	✗
Total preordenado	✗	✗	Y	✗	✗	✗	Y	✗	✗
Orden total	✗	Y	Y	✗	✗	✗	Y	✗	✗
Prewellordering	✗	✗	Y	Y	✗	✗	Y	✗	✗
Bien ordenado	✗	✗	✗	Y	✗	✗	Y	✗	✗
Bien ordenado	✗	Y	Y	Y	✗	✗	Y	✗	✗
Lattice	✗	Y	✗	✗	Y	Y	Y	✗	✗
Join-semilattice	✗	Y	✗	✗	Y	✗	Y	✗	✗
Meet-semilattice	✗	Y	✗	✗	✗	Y	Y	✗	✗
Orden parcial estricta	✗	Y	✗	✗	✗	✗	✗	Y	Y
Orden débil estricto	✗	Y	✗	✗	✗	✗	✗	Y	Y
Orden total estricta	✗	Y	Y	✗	✗	✗	✗	Y	Y
	Simétrico	Antisymmetric	Conectado	Bien fundada	Has joineds	Has meets	Reflexivo	Irreflexivo	Asimétrica
Definiciones, para todos $a,b$ y ${displaystyle Sneq varnothing:}$	${displaystyle {begin{aligned}&aRb\Rightarrow {}&bRaend{aligned}}}$	${displaystyle {begin{aligned}aRb{text{ and }}&bRa\Rightarrow a={}&bend{aligned}}}$	${displaystyle {begin{aligned}aneq {}&bRightarrow \aRb{text{ or }}&bRaend{aligned}}}$	${displaystyle {begin{aligned}min S\{text{exists}}end{aligned}}}$	${displaystyle {begin{aligned}avee b\{text{exists}}end{aligned}}}$	${displaystyle {begin{aligned}awedge b\{text{exists}}end{aligned}}}$	${displaystyle aRa}$	${displaystyle {text{not }}aRa}$	${displaystyle {begin{aligned}aRbRightarrow \{text{not }}bRaend{aligned}}}$

Y indica que la propiedad de la columna es siempre verdad el término de la fila (a la izquierda), mientras que ✗ indica que la propiedad no está garantizada en general (puede, o no, mantener). Por ejemplo, que cada relación de equivalencia es simétrica, pero no necesariamente antisimétrica, se indica por

Y en la columna "Simétrica" y ✗ en la columna "Antisimétrica", respectivamente.

Todas las definiciones requieren tácitamente la relación homogénea $R$ ser transitivo: para todos $a,b,c,$ si ${displaystyle aRb}$ y ${displaystyle bRc}$ entonces ${displaystyle aRc.}$
La definición de un término puede requerir propiedades adicionales que no se enumeran en esta tabla.

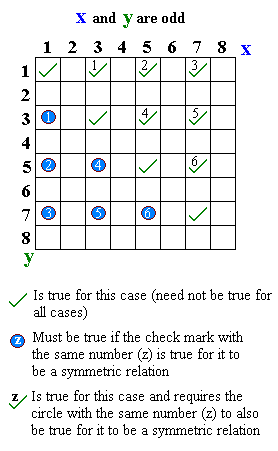
Una relación simétrica es un tipo de relación binaria. Un ejemplo es la relación "es igual a", porque si a = b es verdadera entonces b = a también es cierto. Formalmente, una relación binaria R sobre un conjunto X es simétrica si:

{displaystyle forall a,bin X(aRbLeftrightarrow bRa),}

donde la notación ${displaystyle aRb}$ significa que ${displaystyle (a,b)in R}$ .

Si R^T representa el inverso de R, entonces R es simétrico si y solo si R = R^T.

La simetría, junto con la reflexividad y la transitividad, son las tres propiedades definitorias de una relación de equivalencia.

Ejemplos

En matemáticas

"es igual a" (igualdad) (como "es menor que" no es simétrico)
"es comparable a", para elementos de un conjunto parcialmente ordenado
"... y... son extraños":

Afuera de las matemáticas

"está casado con" (en la mayoría de los sistemas legales)
"es un hermano completamente biológico de"
"es un homófono de"
"es co-trabajador de"
"es compañero de equipo"

Relación con relaciones asimétricas y antisimétricas

Relaciones simétricas y antisimétricas

Por definición, una relación no vacía no puede ser tanto simétrica como asimétrica (donde si a está relacionado con b, entonces b no puede estar relacionado a a (de la misma manera)). Sin embargo, una relación no puede ser ni simétrica ni asimétrica, como es el caso de "es menor o igual que" y "presas de").

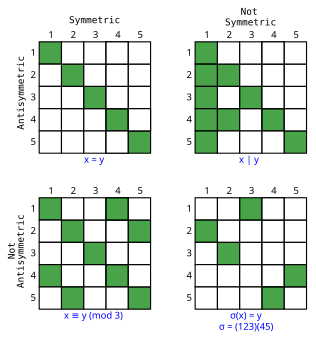
Simétrico y antisimétrico (donde la única forma en que a puede estar relacionado con b y b estar relacionado con a es si a = b) son en realidad independientes entre sí, como muestran estos ejemplos.

Ejemplos matemáticos
	Simétrico	No simétrica
Antisymmetric	igualdad	divide, inferior o igual a
No antisimétrico	congruencia en aritmética modular	// (división de números enteros), la mayoría de las permutaciones no

Ejemplos no matemáticos
	Simétrico	No simétrica
Antisymmetric	es la misma persona que, y está casada	es el plural de
No antisimétrico	es un hermano biológico completo	presas en

Propiedades

Una relación simétrica y transitiva siempre es cuasiflexiva.

Una relación simétrica, transitiva y reflexiva se llama una relación de equivalencia.

Una manera de contar las relaciones simétricas con elementos n, que en su representación matriz binaria el triángulo superior derecho determina la relación totalmente, y puede ser arbitraria dada, por lo tanto hay tantas relaciones simétricas como matrices de triángulo superior nxn binaria, ${displaystyle 2^{n(n+1)/2}.}$

Número de n-element binario relations of different types
Miembros	Cualquier	Transitive	Reflexivo	Simétrico	Preorden	Orden parcial	Total preordenado	Orden total	Equivalencia relación
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65.536	3.994	4.096	1.024	355	219	75	24	15
n	2^n²		2^n²−n	2^n()n+1)/2			${textstyle sum _{k=0}^{n}k!S(n,k)}$	n!	${textstyle sum _{k=0}^{n}S(n,k)}$
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

Tenga en cuenta que $S (n, k)$ se refiere a los números de Stirling del segundo tipo

Contenido relacionado

Más resultados...