Relación Ramberg-Osgood

La ecuación de Ramberg-Osgood se creó para describir la relación no lineal entre la tensión y la deformación (es decir, la curva de tensión-deformación) en materiales cerca de sus puntos de fluencia. Es especialmente aplicable a metales que se endurecen con la deformación plástica (véase endurecimiento por deformación), mostrando una transición elástica-plástica suave. Como se trata de un modelo fenomenológico, es esencial comprobar el ajuste del modelo con datos experimentales reales para el material de interés en particular.

En su forma original, la ecuación para la deformación es

${\displaystyle \varepsilon ={\frac {\sigma ¿Qué? - Sí.$

aquí

${\displaystyle \varepsilon }$ es tensión,

${\displaystyle \sigma }$ es estrés,

${\displaystyle E}$ es el módulo de Young, y

${\displaystyle K}$ y ${\displaystyle n}$ son constantes que dependen del material que se está considerando. En esta forma, K y n no son los mismos que las constantes comúnmente vistas en la ecuación Hollomon.

La ecuación está esencialmente asumiendo la porción de cepa elástica de la curva de entrenamiento de estrés, ${\displaystyle \varepsilon _{e}$, se puede modelar con una línea, mientras que la porción de plástico, ${\displaystyle \varepsilon _{p}$, puede ser modelado con una ley de poder. Los componentes elásticos y plásticos se resumen para encontrar la cepa total.

${\displaystyle \varepsilon =\varepsilon ¿Por qué? ¿Qué?$

El primer término en el lado derecho, ${\displaystyle {\sigma}/{E}\,}$, es igual a la parte elástica de la cepa, mientras que el segundo término, ${\displaystyle \ K({\sigma }/{E} {n}}$, cuentas de la parte de plástico, los parámetros ${\displaystyle K}$ y ${\displaystyle n}$ describiendo comportamiento de endurecimiento del material. Presentación de la rendimiento del material, ${\displaystyle \sigma ¿Qué?$, y definir un nuevo parámetro, ${\displaystyle \alpha }$, relacionado con ${\displaystyle K}$ como ${\displaystyle \alpha =K({\sigma ¿Qué?$, es conveniente reescribir el término en el lado derecho extremo como sigue:

${\displaystyle \ K\left({\frac {\sigma Bien. #frac {\sigma - ¿Qué? - Sí.$

Reemplazando la primera expresión, la ecuación de Ramberg-Osgood se puede escribir como

${\displaystyle \varepsilon ={\frac {\sigma {\fnMicrosoft}\fnMicroc {\sigma - ¿Qué? - Sí.$

En la última forma del modelo Ramberg-Osgood, el comportamiento de endurecimiento del material depende de las constantes materiales ${\displaystyle \alpha \,}$ y ${\displaystyle n\,}$. Debido a la relación poder-ley entre estrés y cepa plástica, el modelo Ramberg-Osgood implica que la cepa plástica está presente incluso para niveles muy bajos de estrés. Sin embargo, para las bajas tensiones aplicadas y para los valores comúnmente utilizados de las constantes materiales ${\displaystyle \alpha }$ y ${\displaystyle n}$, la cepa plástica sigue siendo insignificante en comparación con la cepa elástica. Por otro lado, para niveles de estrés superiores a los ${\displaystyle \sigma ¿Qué?$, la cepa plástica se vuelve progresivamente más grande que la cepa elástica.

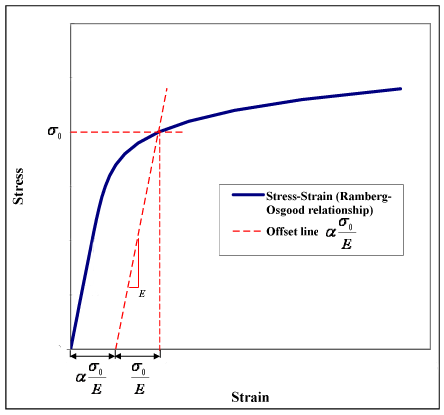
El valor ${\displaystyle \alpha {\frac {\sigma - Sí.$ puede ser visto como offset, como se muestra en la figura 1. Esto viene del hecho de que ${\displaystyle \varepsilon =(1+\alpha){{\sigma .$, cuando ${\displaystyle \sigma =\sigma _{0}\,}$.

En consecuencia, (ver Figura 1):

cepa elástica al rendimiento = ${\displaystyle {\sigma ¿Qué?$

cepa plástica al rendimiento = ${\displaystyle \alpha ({\sigma _{0}/E)\,}$ = offset

Valores usados comúnmente para ${\displaystyle n\,}$ son ~5 o mayor, aunque los valores más precisos se obtienen generalmente por la fijación de datos experimentales de tensil (o compresivo). Valores para ${\displaystyle \alpha \,}$ también se puede encontrar mediante el ajuste a los datos experimentales, aunque para algunos materiales, se puede fijar para tener el offset igual al valor aceptado de la cepa del 0,2%, lo que significa:

${\displaystyle \alpha {\frac {\sigma - Sí.$

Se pueden encontrar varias formulaciones alternativas ligeramente diferentes de la ecuación de Ramberg-Osgood. Como los modelos son puramente empíricos, a menudo resulta útil probar diferentes modelos y comprobar cuál se ajusta mejor al material elegido.

La ecuación Ramberg-Osgood también se puede expresar utilizando los parámetros Hollomon donde ${\displaystyle K}$ es el coeficiente de resistencia (Pa) y ${\displaystyle n}$ es el coeficiente de endurecimiento de la tensión (no unidades).

${\displaystyle \varepsilon ={\frac {\sigma ¿Qué? - Sí.$

Alternativamente, si el estrés del rendimiento, ${\displaystyle \sigma _{y}$, se supone que está en la cepa offset del 0,2%, la siguiente relación puede ser derivada. Note que ${\displaystyle n}$ se define de nuevo en la ecuación original Ramberg-Osgood y es el inverso del coeficiente de endurecimiento de la tensión del Hollomon.

${\displaystyle \varepsilon ={\frac {\sigma }+0.002\left({\frac {\sigma - Sí.$

• Viscoplasticidad#Johnson – Modelo de tensión de flujo de gancho