Relación dosis-respuesta

La relación dosis-respuesta, o relación exposición-respuesta, describe la magnitud de la respuesta de un organismo, en función de la exposición (o dosis) a un estímulo o factor estresante (normalmente una sustancia química) después de un tiempo de exposición determinado. Las relaciones dosis-respuesta se pueden describir mediante curvas dosis-respuesta. Esto se explica con más detalle en las siguientes secciones. Una función estímulo-respuesta o curva estímulo-respuesta se define de forma más amplia como la respuesta a cualquier tipo de estímulo, no limitado a las sustancias químicas.
Motivación para estudiar las relaciones dosis-respuesta
El estudio de la respuesta a la dosis y el desarrollo de modelos de dosis-respuesta son fundamentales para determinar los niveles y dosis "seguros", "peligrosos" y (cuando sea pertinente) beneficiosos de los medicamentos, contaminantes, alimentos y otras sustancias a las que están expuestos los seres humanos u otros organismos. Estas conclusiones suelen ser la base de las políticas públicas. La Agencia de Protección Ambiental de los Estados Unidos ha desarrollado una amplia guía e informes sobre el modelado y la evaluación de la respuesta a la dosis, así como software. La Administración de Alimentos y Medicamentos de los Estados Unidos también tiene una guía para dilucidar las relaciones dosis-respuesta durante el desarrollo de medicamentos. Las relaciones dosis-respuesta se pueden utilizar en individuos o en poblaciones. El adagio La dosis hace el veneno refleja cómo una pequeña cantidad de una toxina no tiene un efecto significativo, mientras que una gran cantidad puede ser mortal. Esto refleja cómo se pueden utilizar las relaciones dosis-respuesta en individuos. En las poblaciones, las relaciones dosis-respuesta pueden describir la forma en que grupos de personas u organismos se ven afectados en diferentes niveles de exposición. Las relaciones dosis-respuesta modeladas mediante curvas dosis-respuesta se utilizan ampliamente en farmacología y desarrollo de fármacos. En particular, la forma de la curva dosis-respuesta de un fármaco (cuantificada mediante los parámetros EC50, nH e ymax) refleja la actividad biológica y la potencia del fármaco.
Ejemplos de estímulos y respuestas
En las tablas que aparecen a continuación se muestran algunos ejemplos de medidas de las relaciones dosis-respuesta. Cada estímulo sensorial se corresponde con un receptor sensorial particular, por ejemplo, el receptor nicotínico de acetilcolina para la nicotina, o el mecanorreceptor para la presión mecánica. Sin embargo, los estímulos (como las temperaturas o la radiación) también pueden afectar a los procesos fisiológicos más allá de la sensación (e incluso dar la respuesta mensurable de la muerte). Las respuestas se pueden registrar como datos continuos (por ejemplo, la fuerza de la contracción muscular) o datos discretos (por ejemplo, el número de muertes).
| Ejemplo | Meta | |
|---|---|---|
| Dosis de fármaco/toxina | Agonista (por ejemplo, nicotina, isoprenalina) | Receptores bioquímicos, Enzymes, Transportadores |
| Antagonista (por ejemplo, ketamina, propranolol) | ||
| Modulador alosterérico (por ejemplo, Benzodiazepina) | ||
| Temperatura | Receptores de temperatura | |
| Niveles de sonido | Células de pelo | |
| Iluminación/Intensidad de luz | Fotoreceptores | |
| Presión mecánica | Mechanoreceptores | |
| Dosis patógena (por ejemplo, LPS) | n/a | |
| Intensidad de radiación | n/a | |
| Nivel de sistema | Respuesta del ejemplo |
|---|---|
| Población (Epidemiología) | Muerte, pérdida de conciencia |
| Organism/whole animal (Physiology) | Severidad de lesión, presión arterial, frecuencia cardíaca, extensión de movimiento, atención, datos EEG |
| Organ/Tissue | Producción ATP, proliferación, contracción muscular, producción bilis, muerte celular |
| Celular (biología celular, bioquímica) | Producción ATP, señales de calcio, morfología, mitosis |
Análisis y creación de curvas dosis-respuesta
Construcción de curvas dosis-respuesta
Una curva dosis-respuesta es un gráfico de coordenadas que relaciona la magnitud de una dosis (estímulo) con la respuesta de un sistema biológico. Se pueden estudiar varios efectos (o puntos finales). La dosis aplicada se representa generalmente en el eje X y la respuesta en el eje Y. En algunos casos, es el logaritmo de la dosis lo que se representa en el eje X. La curva es típicamente sigmoidea, con la parte más pronunciada en el medio. Los modelos basados en la biología que utilizan la dosis son preferibles al uso de log(dosis) porque este último puede implicar visualmente una dosis umbral cuando en realidad no existe ninguna.
El análisis estadístico de las curvas dosis-respuesta se puede realizar mediante métodos de regresión como el modelo probit o el modelo logit, u otros métodos como el método de Spearman-Kärber. Los modelos empíricos basados en la regresión no lineal suelen preferirse al uso de alguna transformación de los datos que linealice la relación dosis-respuesta.
Los diseños experimentales típicos para medir las relaciones dosis-respuesta son las preparaciones de baños de órganos, los ensayos de unión de ligandos, los ensayos funcionales y los ensayos clínicos de fármacos.
En relación con la respuesta a las dosis de radiación, la Health Physics Society (en los Estados Unidos) ha publicado una serie documental sobre los orígenes del modelo lineal sin umbral (LNT), aunque la sociedad no ha adoptado una política al respecto."
Ecuación de Hill
Las curvas dosis-respuesta logarítmicas suelen tener forma sigmoidea y son monótonas, y pueden ajustarse a una ecuación clásica de Hill. La ecuación de Hill es una función logística con respecto al logaritmo de la dosis y es similar a un modelo logit. También se ha sugerido un modelo generalizado para casos multifásicos.
La ecuación Hill es la siguiente fórmula, donde es la magnitud de la respuesta, es la concentración de drogas (o equivalente, intensidad de estímulo) y es la concentración de drogas que produce una respuesta máxima del 50% y es el coeficiente Hill.
Los parámetros de la curva dosis-respuesta reflejan medidas de potencia (como EC50, IC50, ED50, etc.) y medidas de eficacia (como la respuesta tisular, celular o poblacional).
Una curva dosis-respuesta que se utiliza con frecuencia es la curva CE50, la mitad de la concentración máxima efectiva, donde el punto CE50 se define como el punto de inflexión de la curva.
Las curvas de respuesta a la dosis se ajustan normalmente a la ecuación de Hill.
El primer punto del gráfico en el que se alcanza una respuesta superior a cero (o superior a la respuesta de control) se suele denominar dosis umbral. En el caso de la mayoría de las drogas beneficiosas o recreativas, los efectos deseados se producen con dosis ligeramente superiores a la dosis umbral. En dosis más altas, aparecen efectos secundarios no deseados que se intensifican a medida que aumenta la dosis. Cuanto más potente sea una sustancia en particular, más pronunciada será esta curva. En situaciones cuantitativas, el eje Y suele estar designado por porcentajes, que se refieren al porcentaje de individuos expuestos que registran una respuesta estándar (que puede ser la muerte, como en el caso de la DL50). Dicha curva se denomina curva dosis-respuesta cuántica, lo que la distingue de una curva dosis-respuesta graduada, en la que la respuesta es continua (ya sea medida o por juicio).
La ecuación de Hill se puede utilizar para describir relaciones dosis-respuesta, por ejemplo, probabilidad de apertura de canal iónico versus concentración de ligando.
La dosis se expresa generalmente en miligramos, microgramos o gramos por kilogramo de peso corporal en el caso de la exposición oral, o en miligramos por metro cúbico de aire ambiente en el caso de la exposición por inhalación. Otras unidades de dosis son moles por peso corporal, moles por animal y, en el caso de la exposición dérmica, moles por centímetro cuadrado.
Modelo Emax
El modelo Emax es una generalización de la ecuación de Hill, en la que se puede establecer un efecto para una dosis cero. Utilizando la misma notación que la anterior, podemos expresar el modelo como:
Compárese con un reordenamiento de Hill:
El modelo Emax es el modelo más común para describir la relación dosis-respuesta en el desarrollo de fármacos.
Forma de la curva dosis-respuesta
La forma de la curva dosis-respuesta depende generalmente de la topología de la red de reacción objetivo. Si bien la forma de la curva suele ser monótona, en algunos casos se pueden observar curvas dosis-respuesta no monótonas.
Limitaciones
El concepto de relación dosis-respuesta lineal, umbrales y respuestas de todo o nada pueden no ser aplicables a situaciones no lineales. Un modelo de umbral o un modelo lineal sin umbral puede ser más apropiado, dependiendo de las circunstancias. Una crítica reciente de estos modelos en su aplicación a los disruptores endocrinos aboga por una revisión sustancial de los modelos de prueba y toxicológicos a dosis bajas debido a la no monotonía observada, es decir, curvas dosis/respuesta en forma de U.
Las relaciones dosis-respuesta generalmente dependen del tiempo y la vía de exposición (p. ej., inhalación, ingesta alimentaria); la cuantificación de la respuesta después de un tiempo de exposición diferente o por una vía diferente conduce a una relación diferente y posiblemente a conclusiones diferentes sobre los efectos del factor estresante en consideración. Esta limitación se debe a la complejidad de los sistemas biológicos y a los procesos biológicos a menudo desconocidos que operan entre la exposición externa y la respuesta celular o tisular adversa.
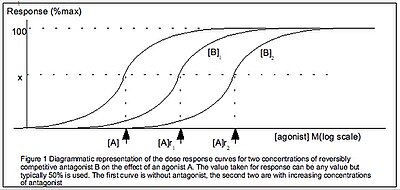
Análisis de SchildEl análisis de Schild también puede proporcionar información sobre el efecto de los medicamentos.

![{\displaystyle {\ce {[A]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/881146b6653b24508d87e34a81c84832f1d5ffea)


![{\displaystyle {\frac {E}{E_{\mathrm {max} }}}={\frac {[A]^{n}}{{\text{EC}}_{50}^{n}+[A]^{n}}}={\frac {1}{1+\left({\frac {\mathrm {EC} _{50}}{[A]}}\right)^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f925d0aa80958bffa0823bb0af1776f883c85e0)
![{\displaystyle E=E_{0}+{\frac {{[A]}^{n}\times {E_{\mathrm {max} }}}{{[A]}^{n}+\mathrm {EC} _{50}^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba22280d1fc6d1db52bf0ae46800e77d582b632f)
![{\displaystyle E_{\mathrm {hill} }={\frac {{[A]}^{n}\times {E_{\mathrm {max} }}}{{[A]}^{n}+\mathrm {EC} _{50}^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12552d523bba224b4d70fea7e1cbbc2d6781792a)