Relación de onda estacionaria

Compartir Imprimir Citar

Medida utilizada en la ingeniería radiofónica y las telecomunicaciones

En ingeniería de radio y telecomunicaciones, la relación de onda estacionaria (SWR) es una medida de adaptación de impedancia de las cargas a la impedancia característica de una línea de transmisión o guía de ondas. Los desajustes de impedancia dan como resultado ondas estacionarias a lo largo de la línea de transmisión, y SWR se define como la relación entre la amplitud de la onda estacionaria parcial en un antinodo (máximo) y la amplitud en un nodo (mínimo) a lo largo de la línea.

La ROE generalmente se considera en términos de los voltajes de CA máximos y mínimos a lo largo de la línea de transmisión, por lo que se denomina relación de onda estacionaria de voltaje o VSWR (a veces pronunciado & #34;vizwar"). Por ejemplo, el valor VSWR 1,2:1 significa que un voltaje de CA, debido a las ondas estacionarias a lo largo de la línea de transmisión, tendrá un valor máximo 1,2 veces mayor que el voltaje de CA mínimo a lo largo de esa línea, si la línea tiene al menos la mitad de la longitud de onda. largo. La ROE también se puede definir como la relación entre la amplitud máxima y la amplitud mínima de las corrientes de la línea de transmisión, la intensidad del campo eléctrico o la intensidad del campo magnético. Sin tener en cuenta la pérdida de la línea de transmisión, estas relaciones son idénticas.

La relación de onda estacionaria de potencia (PSWR) se define como el cuadrado de la VSWR; sin embargo, este término en desuso no tiene una relación física directa con la potencia realmente involucrada en la transmisión..

La ROE generalmente se mide con un instrumento dedicado llamado medidor de ROE. Dado que SWR es una medida de la impedancia de carga relativa a la impedancia característica de la línea de transmisión en uso (que en conjunto determinan el coeficiente de reflexión como se describe a continuación), un medidor de SWR dado puede interpretar la impedancia que ve en términos de SWR solo si tiene diseñado para la misma impedancia característica particular que la línea. En la práctica, la mayoría de las líneas de transmisión utilizadas en estas aplicaciones son cables coaxiales con una impedancia de 50 o 75 ohmios, por lo que la mayoría de los medidores de ROE corresponden a uno de estos.

Comprobar la SWR es un procedimiento estándar en una estación de radio. Aunque se podría obtener la misma información midiendo la impedancia de la carga con un analizador de impedancia (o "puente de impedancia"), el medidor SWR es más simple y robusto para este propósito. Al medir la magnitud del desajuste de impedancia en la salida del transmisor, se revelan problemas debido a la antena o la línea de transmisión.

Coincidencia de impedancia

SWR se utiliza como una medida de adaptación de la impedancia de una carga a la impedancia característica de una línea de transmisión que transporta señales de radiofrecuencia (RF). Esto se aplica especialmente a las líneas de transmisión que conectan transmisores y receptores de radio con sus antenas, así como a usos similares de cables de RF, como conexiones de televisión por cable a receptores de TV y amplificadores de distribución. La adaptación de impedancia se logra cuando la impedancia de la fuente es el complejo conjugado de la impedancia de la carga. La forma más fácil de lograr esto, y la forma que minimiza las pérdidas a lo largo de la línea de transmisión, es que la parte imaginaria de la impedancia compleja tanto de la fuente como de la carga sea cero, es decir, resistencias puras, igual a la impedancia característica de la línea de transmisión. Cuando hay una discrepancia entre la impedancia de carga y la línea de transmisión, parte de la onda directa enviada hacia la carga se refleja a lo largo de la línea de transmisión hacia la fuente. Entonces, la fuente ve una impedancia diferente de la que espera, lo que puede llevar a que suministre menos (o en algunos casos, más) potencia, siendo el resultado muy sensible a la longitud eléctrica de la línea de transmisión.

Tal desajuste generalmente no es deseado y da como resultado ondas estacionarias a lo largo de la línea de transmisión que magnifican las pérdidas de la línea de transmisión (significativas a frecuencias más altas y para cables más largos). La SWR es una medida de la profundidad de esas ondas estacionarias y, por lo tanto, es una medida de la adaptación de la carga a la línea de transmisión. Una carga adaptada daría como resultado una ROE de 1:1, lo que implica que no hay onda reflejada. Una SWR infinita representa la reflexión completa de una carga incapaz de absorber energía eléctrica, con toda la energía incidente reflejada hacia la fuente.

Debe entenderse que la coincidencia de una carga con la línea de transmisión es diferente de la coincidencia de una fuente con la línea de transmisión o la coincidencia de una fuente con la carga vista a través la línea de transmisión. Por ejemplo, si hay una coincidencia perfecta entre la impedancia de carga $Z$ _load y la impedancia de origen $Z$ _fuente = $Z$ ^*_load, esa combinación perfecta permanecerá si la fuente y la carga están conectadas a través de una transmisión línea con una longitud eléctrica de media longitud de onda (o un múltiplo de media longitud de onda) usando una línea de transmisión de cualquier impedancia característica $Z$ ₀. Sin embargo, la SWR generalmente no será 1:1, dependiendo únicamente de $Z$ _load y Z₀. Con una longitud diferente de la línea de transmisión, la fuente verá una impedancia diferente a la $Z$ _load que puede o puede no ser una buena coincidencia con la fuente. A veces, esto es deliberado, como cuando se utiliza una sección de adaptación de un cuarto de onda para mejorar la adaptación entre una fuente y una carga que, de lo contrario, no coincidirían.

Sin embargo, las fuentes de RF típicas, como los transmisores y los generadores de señales, están diseñadas para analizar una impedancia de carga puramente resistiva, como 50 Ω o 75 Ω, correspondiente a las líneas de transmisión comunes. impedancias características. En esos casos, haciendo coincidir la carga con la línea de transmisión, $Z$ _load = $Z$ ₀, siempre asegura que la fuente verá la misma impedancia de carga como si la transmisión línea no estaban allí. Esto es idéntico a una SWR de 1:1. Esta condición ( $Z$ _load = $Z$ ₀) también significa que la carga vista por la fuente es independiente de la longitud eléctrica de la línea de transmisión. Dado que la longitud eléctrica de un segmento físico de la línea de transmisión depende de la frecuencia de la señal, la violación de esta condición significa que la impedancia vista por la fuente a través de la línea de transmisión se convierte en función de la frecuencia (especialmente si la línea es larga), incluso si $Z$ _load es independiente de la frecuencia. Entonces, en la práctica, una buena SWR (cerca de 1: 1) implica que la salida de un transmisor vea la impedancia exacta que espera para una operación óptima y segura.

Relación con el coeficiente de reflexión

La onda de incidentes (azul) se refleja completamente (ola roja) fuera de fase en el extremo cortocircuito de la línea de transmisión, creando una onda de tensión (negro). Dimensiones = 1, SWR = ∞.

Ondas permanentes en línea de transmisión, voltaje neto mostrado en diferentes colores durante un período de oscilación. La onda entrante de izquierda (amplitud = 1) se refleja parcialmente con (de arriba a abajo) Dimensiones = 0,6 −0,333 y 0,8 ∠60°. SWR resultante = 4, 2, 9.

El componente de tensión de una onda de pie en una línea de transmisión uniforme consiste en la onda de avance (con amplitud compleja) $V_{f}$ ) superpuesto en la onda reflejada (con amplitud compleja) $V_{r}$ ).

Una ola se refleja en parte cuando una línea de transmisión se termina con una impedancia desigual a su impedancia característica. El coeficiente de reflexión $Gamma$ puede definirse como:

{displaystyle Gamma ={frac {V_{r}}{V_{f}}}.}

{displaystyle Gamma ={Z_{L}-Z_{o} over Z_{L}+Z_{o}}}

$Gamma$ es un número complejo que describe tanto la magnitud como el cambio de fase de la reflexión. Los casos más simples con $Gamma$ medida en la carga son:

${displaystyle Gamma =-1}$ : completa reflexión negativa, cuando la línea es corta,
$Gamma =0$ : sin reflexión, cuando la línea es perfectamente igualada,
${displaystyle Gamma =+1}$ : completa reflexión positiva, cuando la línea está abierta.

El SWR corresponde directamente a la magnitud de $Gamma$ .

En algunos puntos a lo largo de la línea las ondas hacia adelante y reflejadas interfieren constructivamente, exactamente en fase, con la amplitud resultante $V_text{max}$ dada por la suma de las amplitudes de esas olas:

{displaystyle {begin{aligned}|V_{text{max}}|&=|V_{f}|+|V_{r}|\&=|V_{f}|+|Gamma V_{f}|\&=(1+|Gamma |)|V_{f}|.end{aligned}}}

En otros puntos, las ondas interfieren 180° fuera de fase con las amplitudes cancelándose parcialmente:

{displaystyle {begin{aligned}|V_{text{min}}|&=|V_{f}|-|V_{r}|\&=|V_{f}|-|Gamma V_{f}|\&=(1-|Gamma |)|V_{f}|.end{aligned}}}

La relación de onda estacionaria de voltaje es entonces

{displaystyle {text{VSWR}}={frac {|V_{text{max}}|}{|V_{text{min}}|}}={frac {1+|Gamma |}{1-|Gamma |}}.}

Desde la magnitud de la $Gamma$ Siempre cae en el rango [0,1], el SWR siempre es mayor o igual a la unidad. Note que fase de V_f y V_r varían a lo largo de la línea de transmisión en direcciones opuestas entre sí. Por lo tanto, el coeficiente de reflexión de valor complejo $Gamma$ varía también, pero sólo en fase. Con el SWR dependiente sólo sobre la magnitud compleja $Gamma$ , se puede ver que el SWR medido en cualquiera El punto a lo largo de la línea de transmisión (por ejemplo, pérdidas de línea de transmisión) obtiene una lectura idéntica.

Dado que la potencia de las ondas directa y reflejada es proporcional al cuadrado de los componentes de voltaje debido a cada onda, SWR se puede expresar en términos de potencia directa y reflejada:

{displaystyle {text{SWR}}={frac {1+{sqrt {P_{r}/P_{f}}}}{1-{sqrt {P_{r}/P_{f}}}}}.}

Al muestrear el voltaje y la corriente complejos en el punto de inserción, un medidor SWR puede calcular los voltajes directos y reflejados efectivos en la línea de transmisión para la impedancia característica para la cual se diseñó el medidor SWR. Dado que la potencia directa y reflejada está relacionada con el cuadrado de los voltajes directo y reflejado, algunos medidores SWR también muestran la potencia directa y reflejada.

En el caso especial de una carga $R$ _L, que es puramente resistiva pero desigual a la impedancia característica de la línea de transmisión $Z$ ₀, la SWR viene dada simplemente por su relación:

{displaystyle {text{SWR}}=max left{{frac {R_{text{L}}}{,Z_{text{0}},}},,{frac {,Z_{text{0}},}{R_{text{L}}}}right}}

con la razón o su recíproco se elige para obtener un valor mayor a la unidad.

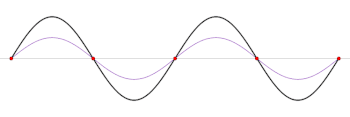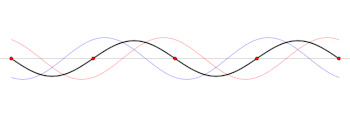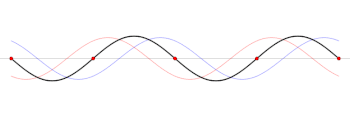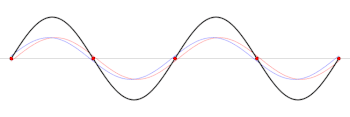
El patrón de onda estacionaria

Usando notación compleja para las amplitudes de tensión, para una señal a frecuencia ${displaystyle nu}$ los voltajes V reales_efectivos como función del tiempo $t$ se entiende que se relacionan con los voltajes complejos según:

{displaystyle V_{text{actual}}={mathcal {R_{e}}}(e^{i2pi nu t}V)~.}

Así, tomando la parte real de la cantidad compleja entre paréntesis, el voltaje real consiste en una onda sinusoidal a la frecuencia ν con una amplitud máxima igual a la magnitud compleja de $V$ , y con una fase dada por la fase del complejo $V$ . Luego, con la posición a lo largo de una línea de transmisión dada por $x$ , con la línea que termina en una carga ubicada en $x$ ₀, las amplitudes complejas de las ondas directa e inversa se escribirían como:

{begin{aligned}V_{f}(x)&=e^{-ik(x-x_{0})}A\V_{r}(x)&=Gamma e^{ik(x-x_{0})}Aend{aligned}}

para alguna amplitud compleja $A$ (correspondiente a la onda delantera $x$ ₀). Aquí. $k$ es el número de onda debido a la longitud de onda guiada a lo largo de la línea de transmisión. Tenga en cuenta que algunos tratamientos usan fáseres donde la dependencia del tiempo es según $e^{-i2pi nu t}$ y dependencia espacial (para una ola en la $+x$ dirección) $e^{+ik(x-x_{0})}$ . Cualquier convención obtiene el mismo resultado para $V$ _efectivos.

Según el principio de superposición, la tensión neta presente en cualquier punto $x$ de la línea de transmisión es igual a la suma de las Voltajes debidos a las ondas directa y reflejada:

{displaystyle {begin{aligned}V_{text{net}}(x)&=V_{f}(x)+V_{r}(x)\&=e^{-ik(x-x_{0})}left(1+Gamma e^{i2k(x-x_{0})}right)Aend{aligned}}}

Ya que estamos interesados en las variaciones de la magnitud de $V$ _net a lo largo de la línea (como una función de $x$ ), resolveremos en cambio para la magnitud al cuadrado de esa cantidad, que simplifica las matemáticas. Para obtener la magnitud al cuadrado, multiplicamos la cantidad anterior por su complejo conjugado:

{displaystyle {begin{aligned}|V_{text{net}}(x)|^{2}&=V_{text{net}}(x)V_{text{net}}^{*}(x)\&=e^{-ik(x-x_{0})}left(1+Gamma e^{i2k(x-x_{0})}right)A,e^{+ik(x-x_{0})}left(1+Gamma ^{*}e^{-i2k(x-x_{0})}right)A^{*}\&=left[1+|Gamma |^{2}+2,operatorname {mathcal {R_{e}}} (Gamma e^{i2k(x-x_{0})})right]|A|^{2}end{aligned}}}

Dependiendo de la fase del tercer mandato, los valores máximos y mínimos $V$ _neto (la raíz cuadrada de la cantidad en las ecuaciones) son ${displaystyle (1+|Gamma |)|A|}$ y ${displaystyle (1-|Gamma |)|A|}$ respectivamente, por una relación de onda fija de:

{displaystyle {text{SWR}}={frac {|V_{text{max}}|}{|V_{text{min}}|}}={frac {1+|Gamma |}{1-|Gamma |}}}

{displaystyle |Gamma |={frac {{text{SWR}}-1}{{text{SWR}}+1}}}

como se afirmó anteriormente. A lo largo de la línea, la expresión anterior para $|V_{text{net}}(x)|^{2}$ se ve oscilar sinusoidalmente entre $|V_{text{min}}|^{2}$ y $|V_{text{max}}|^{2}$ con un período 2 $π$ /2 $k$ . Esto es mitad de la longitud de onda guiada $λ$ = 2 $π$ / $k$ para la frecuencia $.$ . Eso se puede ver como debido a la interferencia entre dos olas de esa frecuencia que están viajando opuesto direcciones.

Por ejemplo, a una frecuencia ν = 20 MHz (longitud de onda en el espacio libre de 15 m) en una línea de transmisión cuyo factor de velocidad es 2/3, la longitud de onda guiada (distancia entre los picos de voltaje de la onda directa sola) sería $λ$ = 10 m. En los casos en que la onda hacia adelante en $x$ = 0 está en fase cero (voltaje máximo) y luego en $x$ = 10 m también estaría en fase cero, pero en $x$ = 5 m sería a 180° de fase (voltaje negativo pico). Por otro lado, la magnitud del voltaje debido a una onda estacionaria producida por su adición a una onda reflejada, tendría una longitud de onda entre picos de solo 1/2 $λ$ = 5 m. Según la ubicación de la carga y la fase de reflexión, puede haber un pico en la magnitud de $V$ _net en $x$ = 1,3 m. Luego se encontraría otro pico donde |V_net|=V_max en $x$ = 6,3 m, mientras que encontraría los mínimos de la onda estacionaria en $x$ = 3,8 m, 8,8 m, etc.

Implicaciones prácticas de SWR

Ejemplo de ancho de banda estimado de antena según el horario VSWR por la ayuda del Ansys HFSS

El caso más común para medir y examinar SWR es cuando se instalan y sintonizan antenas transmisoras. Cuando un transmisor está conectado a una antena por una línea de alimentación, la impedancia del punto de activación de la antena debe coincidir con la impedancia característica de la línea de alimentación para que el transmisor vea la impedancia para la que fue diseñado (la impedancia de la línea de alimentación, generalmente 50 o 75 ohmios).

La impedancia de un diseño de antena en particular puede variar debido a una serie de factores que no siempre se pueden identificar claramente. Esto incluye la frecuencia del transmisor (en comparación con el diseño de la antena o la frecuencia de resonancia), la altura de la antena por encima y la calidad del suelo, la proximidad a grandes estructuras metálicas y las variaciones en el tamaño exacto de los conductores. utilizado para construir la antena.

Cuando una antena y una línea de alimentación no tienen impedancias coincidentes, el transmisor ve una impedancia inesperada, donde es posible que no pueda producir toda su potencia e incluso puede dañar el transmisor en algunos casos. La potencia reflejada en la línea de transmisión aumenta la corriente promedio y, por lo tanto, las pérdidas en la línea de transmisión en comparación con la potencia realmente entregada a la carga. Es la interacción de estas ondas reflejadas con las ondas directas lo que provoca patrones de ondas estacionarias, con las repercusiones negativas que hemos señalado.

A veces se puede hacer coincidir la impedancia de la antena con la impedancia de la línea de alimentación ajustando la propia antena, pero de lo contrario es posible usando un sintonizador de antena, un dispositivo de igualación de impedancia. La instalación del sintonizador entre la línea de alimentación y la antena permite que la línea de alimentación vea una carga cercana a su impedancia característica, mientras envía la mayor parte de la potencia del transmisor (una pequeña cantidad puede disiparse dentro del sintonizador) para ser radiada por la antena a pesar de su impedancia de punto de alimentación inaceptable. La instalación de un sintonizador entre el transmisor y la línea de alimentación también puede transformar la impedancia que se ve en el extremo del transmisor de la línea de alimentación a la preferida por el transmisor. Sin embargo, en el último caso, la línea de alimentación todavía tiene una alta SWR presente, con el aumento resultante de pérdidas en la línea de alimentación sin mitigar.

La magnitud de esas pérdidas depende del tipo de línea de transmisión y su longitud. Siempre aumentan con la frecuencia. Por ejemplo, una determinada antena utilizada lejos de su frecuencia resonante puede tener una ROE de 6:1. Para una frecuencia de 3,5 MHz, con esa antena alimentada a través de 75 metros de cable coaxial RG-8A, la pérdida debida a las ondas estacionarias sería de 2,2 dB. Sin embargo, el mismo desajuste de 6:1 a través de 75 metros de coaxial RG-8A incurriría en 10,8 dB de pérdida a 146 MHz. Por lo tanto, una mejor adaptación de la antena a la línea de alimentación, es decir, una SWR más baja, se vuelve cada vez más importante con el aumento de la frecuencia, incluso si el transmisor es capaz de adaptarse a la impedancia observada (o si se usa un sintonizador de antena entre el transmisor y la alimentación). línea).

Ciertos tipos de transmisiones pueden sufrir otros efectos negativos por las ondas reflejadas en una línea de transmisión. La televisión analógica puede experimentar "fantasmas" de señales retrasadas que rebotan de un lado a otro en una línea larga. El estéreo FM también puede verse afectado y las señales digitales pueden experimentar pulsos retrasados que conducen a errores de bits. Siempre que los tiempos de retardo de una señal que baja y vuelve a subir son comparables a las constantes de tiempo de modulación, se producen efectos. Por esta razón, estos tipos de transmisiones requieren una SWR baja en la línea de alimentación, incluso si la pérdida inducida por SWR puede ser aceptable y la coincidencia se realiza en el transmisor.

Métodos para medir la relación de ondas estacionarias

Línea Ranurada. La sonda se mueve a lo largo de la línea para medir el voltaje variable. SWR es el máximo dividido por el voltaje mínimo

Se pueden utilizar muchos métodos diferentes para medir la relación de ondas estacionarias. El método más intuitivo utiliza una línea ranurada, que es una sección de la línea de transmisión con una ranura abierta que permite que una sonda detecte el voltaje real en varios puntos a lo largo de la línea.

Por lo tanto, los valores máximo y mínimo se pueden comparar directamente. Este método se utiliza en VHF y frecuencias más altas. A frecuencias más bajas, tales líneas son imprácticamente largas.

Los acopladores direccionales se pueden utilizar en frecuencias de HF a través de microondas. Algunos son de un cuarto de onda o más largos, lo que restringe su uso a las frecuencias más altas. Otros tipos de acopladores direccionales muestrean la corriente y el voltaje en un solo punto en la ruta de transmisión y los combinan matemáticamente para representar la potencia que fluye en una dirección. El tipo común de SWR/medidor de potencia utilizado en operaciones de aficionados puede contener un acoplador direccional dual. Otros tipos usan un solo acoplador que se puede girar 180 grados para muestrear el flujo de energía en cualquier dirección. Los acopladores unidireccionales de este tipo están disponibles para muchos rangos de frecuencia y niveles de potencia y con valores de acoplamiento apropiados para el medidor analógico utilizado.

Un wattímetro direccional utilizando un elemento acoplador direccional giratorio.

La potencia directa y reflejada medida por los acopladores direccionales se puede utilizar para calcular la ROE. Los cálculos se pueden realizar matemáticamente en forma analógica o digital o utilizando métodos gráficos integrados en el medidor como una escala adicional o leyendo desde el punto de cruce entre dos agujas en el mismo medidor. Los instrumentos de medición anteriores se pueden utilizar "en línea" es decir, toda la potencia del transmisor puede pasar a través del dispositivo de medición para permitir el monitoreo continuo de SWR. Otros instrumentos, como analizadores de red, acopladores direccionales de baja potencia y puentes de antena, utilizan baja potencia para la medición y deben conectarse en lugar del transmisor. Los circuitos de puente se pueden usar para medir directamente las partes real e imaginaria de una impedancia de carga y usar esos valores para derivar SWR. Estos métodos pueden proporcionar más información que solo SWR o potencia directa y reflejada. Los analizadores de antena autónomos utilizan varios métodos de medición y pueden mostrar SWR y otros parámetros representados en función de la frecuencia. Al usar acopladores direccionales y un puente en combinación, es posible hacer un instrumento en línea que lea directamente en impedancia compleja o en SWR. También hay disponibles analizadores de antena independientes que miden múltiples parámetros.

Relación de onda estacionaria de potencia

El término relación de ondas estacionarias de potencia (PSWR) a veces se denomina y se define como el cuadrado de la relación de ondas estacionarias de tensión. El término se cita ampliamente como "engañoso".

La expresión "proporción de onda de poder", que a veces se puede encontrar, es aún más engañosa, ya que la distribución de energía a lo largo de una línea libre de pérdidas es constante....
—J.H. Gridley (2014)

Sin embargo, corresponde a un tipo de medición de SWR utilizando lo que anteriormente era un instrumento de medición estándar en frecuencias de microondas, la línea ranurada. La línea ranurada es una guía de ondas (o línea coaxial llena de aire) en la que una pequeña antena de detección que forma parte de un detector de cristal o detector se coloca en el campo eléctrico en la línea. El voltaje inducido en la antena se rectifica mediante un diodo de contacto puntual (rectificador de cristal) o un diodo de barrera Schottky que se incorpora en el detector. Estos detectores tienen una salida de ley cuadrática para bajos niveles de entrada. Por lo tanto, las lecturas correspondieron al cuadrado del campo eléctrico a lo largo de la ranura, E²(x), con lecturas máximas y mínimas de E²_max y E²_min encontrados como sonda se mueve a lo largo de la ranura. La relación de estos produce el cuadrado de la ROE, el llamado PSWR.

Esta técnica de racionalización de términos está plagada de problemas. El comportamiento de la ley cuadrática del diodo detector se exhibe solo cuando el voltaje a través del diodo está por debajo de la rodilla del diodo. Una vez que el voltaje detectado excede la rodilla, la respuesta del diodo se vuelve casi lineal. En este modo, el diodo y su capacitor de filtrado asociado producen un voltaje que es proporcional al pico del voltaje muestreado. El operador de tal detector no tendría una indicación lista en cuanto al modo en el que está funcionando el diodo detector y, por lo tanto, diferenciar los resultados entre SWR o PSWR no es práctico. Quizás aún peor, es el caso común en el que el voltaje mínimo detectado está por debajo de la rodilla y el voltaje máximo está por encima de la rodilla. En este caso, los resultados calculados carecen en gran medida de sentido. Por lo tanto, los términos PSWR y Power Standing Wave Ratio están en desuso y deben considerarse solo desde una perspectiva de medición heredada.

Implicaciones de SWR en aplicaciones médicas

SWR también puede tener un impacto perjudicial en el rendimiento de las aplicaciones médicas basadas en microondas. En la electrocirugía por microondas, es posible que una antena que se coloca directamente en el tejido no siempre tenga una coincidencia óptima con la línea de alimentación, lo que da como resultado una ROE. La presencia de SWR puede afectar los componentes de monitoreo utilizados para medir los niveles de potencia, lo que afecta la confiabilidad de dichas mediciones.

Te puede interesar
Ferroelectricidad
(leer más)
Te puede interesar
Centro de presión (mecánica de fluidos)
(leer más)
Te puede interesar
Constante de propagación
(leer más)
Más resultados...