Relación de elevación a arrastre
En aerodinámica, la relación sustentación-resistencia (o relación L/D) es la sustentación generada por un cuerpo aerodinámico como un perfil aerodinámico o un avión, dividida por la resistencia aerodinámica causada por el movimiento a través del aire. Describe la eficiencia aerodinámica en determinadas condiciones de vuelo. La relación L/D para cualquier cuerpo dado variará según estas condiciones de vuelo.
Para un ala aerodinámica o una aeronave motorizada, la L/D se especifica en vuelo recto y nivelado. Para un planeador, determina la tasa de planeo, de la distancia recorrida frente a la pérdida de altura.
El término se calcula para cualquier velocidad aerodinámica en particular midiendo la sustentación generada y luego dividiéndola por la resistencia a esa velocidad. Estos varían con la velocidad, por lo que los resultados generalmente se trazan en un gráfico bidimensional. En casi todos los casos, el gráfico tiene forma de U, debido a los dos componentes principales de la resistencia. La L/D se puede calcular usando dinámica de fluidos computacional o simulación por computadora. Se mide empíricamente mediante ensayos en túnel de viento o en vuelo libre.
La relación L/D se ve afectada tanto por el arrastre de forma del cuerpo como por el arrastre inducido asociado con la creación de una fuerza de sustentación. Depende principalmente de los coeficientes de sustentación y arrastre, el ángulo de ataque al flujo de aire y la relación de aspecto del ala.
La relación L/D es inversamente proporcional a la energía requerida para una trayectoria de vuelo determinada, por lo que duplicar la relación L/D requerirá solo la mitad de la energía para la misma distancia recorrida. Esto resulta directamente en una mejor economía de combustible.
La relación L/D también se puede utilizar para embarcaciones y vehículos terrestres. Las relaciones L/D para hidroalas y embarcaciones de desplazamiento se determinan de manera similar a las aeronaves.
Levantar y arrastrar


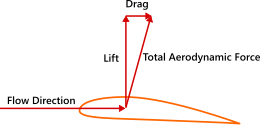
Se puede crear sustentación cuando un cuerpo con forma de perfil aerodinámico viaja a través de un fluido viscoso como el aire. El perfil aerodinámico a menudo está combado y/o colocado en un ángulo de ataque al flujo de aire. La sustentación luego aumenta como el cuadrado de la velocidad del aire.
Siempre que un cuerpo aerodinámico genera sustentación, también crea resistencia inducida por sustentación o resistencia inducida. A bajas velocidades, un avión tiene que generar sustentación con un mayor ángulo de ataque, lo que da como resultado una mayor resistencia inducida. Este término domina el lado de baja velocidad del gráfico de sustentación versus velocidad.
El arrastre de forma es causado por el movimiento del cuerpo a través del aire. Este tipo de arrastre, conocido también como resistencia del aire o arrastre de perfil, varía con el cuadrado de la velocidad (ver ecuación de arrastre). Por esta razón, la resistencia del perfil es más pronunciada a mayores velocidades, formando el lado derecho de la forma de U del gráfico de sustentación/velocidad. El arrastre del perfil se reduce principalmente mediante la racionalización y la reducción de la sección transversal.
La resistencia total de cualquier cuerpo aerodinámico tiene dos componentes, la resistencia inducida y la resistencia de forma.
Coeficientes de sustentación y arrastre
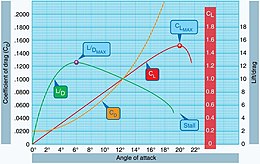
Las tasas de cambio de sustentación y arrastre con el ángulo de ataque (AoA) se denominan respectivamente coeficientes de sustentación y arrastre CL y CD. La relación variable entre sustentación y arrastre con AoA a menudo se representa en términos de estos coeficientes.
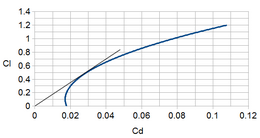
Para cualquier valor dado de sustentación, el AoA varía con la velocidad. Los gráficos de CL y CD frente a la velocidad se denominan curvas de arrastre. La velocidad se muestra aumentando de izquierda a derecha. La relación sustentación/arrastre viene dada por la pendiente desde el origen hasta algún punto de la curva, por lo que la relación L/D máxima no se produce en el punto de menor coeficiente de arrastre, el punto más a la izquierda. En cambio, ocurre a una velocidad ligeramente mayor. Los diseñadores normalmente seleccionarán un diseño de ala que produzca un pico L/D a la velocidad de crucero elegida para un avión de ala fija propulsado, maximizando así la economía. Como todas las cosas en la ingeniería aeronáutica, la relación sustentación-resistencia no es la única consideración para el diseño del ala. El rendimiento en un alto ángulo de ataque y una entrada en pérdida suave también son importantes.
Ratio de planeo
Como el fuselaje de la aeronave y las superficies de control también agregarán resistencia y posiblemente sustentación, es justo considerar la L/D de la aeronave como un todo. La relación de planeo, que es la relación entre el movimiento de avance de una aeronave (sin motor) y su descenso, es (cuando se vuela a velocidad constante) numéricamente igual a la L/D de la aeronave. Esto es especialmente interesante en el diseño y operación de planeadores de alto rendimiento, que pueden tener índices de planeo de casi 60 a 1 (60 unidades de distancia hacia adelante por cada unidad de descenso) en el mejor de los casos, pero 30:1 se considera un buen rendimiento. para uso recreativo general. Lograr la mejor L/D de un planeador en la práctica requiere un control preciso de la velocidad del aire y un funcionamiento suave y restringido de los controles para reducir la resistencia de las superficies de control desviadas. En condiciones de viento cero, L/D será igual a la distancia recorrida dividida por la altitud perdida. Alcanzar la distancia máxima para la altitud perdida en condiciones de viento requiere una modificación adicional de la mejor velocidad aerodinámica, al igual que la alternancia de crucero y térmica. Para lograr una alta velocidad en todo el país, los pilotos de planeadores que anticipan fuertes térmicas a menudo cargan sus planeadores (planeadores) con lastre de agua: el aumento de la carga alar significa una relación de planeo óptima a mayor velocidad aerodinámica, pero a costa de ascender más lentamente en las térmicas. Como se indica a continuación, la L/D máxima no depende del peso ni de la carga alar, pero con una mayor carga alar, la L/D máxima se produce a una velocidad aerodinámica más rápida. Además, la velocidad aerodinámica más rápida significa que la aeronave volará con un mayor número de Reynolds y esto generalmente generará un coeficiente de arrastre de sustentación cero más bajo.
Teoría
Subsónico
Matemáticamente, la relación máxima de elevación a arrastre se puede estimar como:
- ()L/D)max=12π π ε ε ARCD,0,{displaystyle (L/D)_{max }={frac {1}{2}{sqrt {frac {pivarepsilon ¿Qué?
Donde AR es la relación de aspecto, ε ε {displaystyle varepsilon } el factor de eficiencia del lapso, un número menos que pero cerca de la unidad para las alas largas y rectas, y CD,0{displaystyle C_{D,0} el coeficiente de arrastre de elevación cero.
Lo que es más importante, la relación máxima de elevación a arrastre es independiente del peso de la aeronave, el área del ala o la carga alar.
Se puede demostrar que dos factores principales de la máxima relación sustentación-resistencia para un avión de ala fija son la envergadura y el área mojada total. Un método para estimar el coeficiente de arrastre de sustentación cero de una aeronave es el método equivalente de fricción superficial. Para un avión bien diseñado, la resistencia aerodinámica de sustentación cero (o resistencia parásita) se compone principalmente de la resistencia aerodinámica de la piel más un pequeño porcentaje de resistencia aerodinámica causada por la separación del flujo. El método utiliza la ecuación:
- CD,0=CfeSmojadoSref,{displaystyle C_{D,0}=C_{text{fe}{frac {S_{text{wet}} {S_{text{ref}}}}} {f}}} {f}}} {f}}}} {f}}}}}} {f}}}}}} {f}}}}}}}}} {f}
Donde Cfe{displaystyle C_{text{fe}} es el coeficiente de fricción de la piel equivalente, Smojado{displaystyle S_{text{wet}} es el área mojada y Sref{displaystyle S_{text{ref}} es el área de referencia del ala. El coeficiente equivalente de fricción de la piel representa tanto el arrastre de separación como el arrastre de fricción de la piel y es un valor bastante consistente para los tipos de aviones de la misma clase. Sustituir esto en la ecuación para la relación máxima de elevación a deriva, junto con la ecuación para relación de aspecto (b2/Sref{displaystyle B^{2}/S_{text{ref}}), produce la ecuación:
- ()L/D)max=12π π ε ε Cfeb2Smojado{displaystyle (L/D)_{max }={frac {1}{2}{sqrt {{frac {pivarepsilon {fnMicroc} {fnMicroc} {fnK}} {f}}}} {fn}}}}}} {f}}}}} {f}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
Donde b Es el ala. El término b2/Smojado{displaystyle - Sí. se conoce como la relación de aspecto mojado. La ecuación demuestra la importancia de la relación de aspecto mojado para lograr un diseño aerodinámicamente eficiente.
Supersónico
A velocidades muy altas, las relaciones entre sustentación y arrastre tienden a ser más bajas. El Concorde tenía una relación sustentación/resistencia de aproximadamente 7 a Mach 2, mientras que un 747 tiene aproximadamente 17 a aproximadamente Mach 0,85.
Dietrich Küchemann desarrolló una relación empírica para predecir la relación L/D para Mach alto:
- L/Dmax=4()M+3)M{displaystyle L/D_{max }={frac {4(M+3)}{M}}}} {m} {m}}} {m}}}}}} {m} {m}}} {fn}}}}}}}} {m}
where M is the Mach number. Wind Tunnel tests have shown this to be approximately accurate.
Ejemplos de relaciones L/D

- Flecha de casa: 4:1
- Herring gull 10:1
- Común 12:1
- Albatross 20:1
- Wright Flyer 8.3:1
- Boeing 747 en crucero 17.7:1.
- Cruising Airbus A380 20:1
- Concorde en el despegue y aterrizaje 4:1, aumentando a 12:1 en Mach 0.95 y 7.5:1 en Mach 2
- Helicóptero a 100 kn (190 km/h) 4.5:1
- Cessna 172 gliding 10.9:1
- Cruising Lockheed U-2 25.6:1
- Rutan Voyager 27:1
- Virgin Atlantic GlobalFlyer 37:1
| Jetliner | crucero L/D | Primer vuelo |
|---|---|---|
| L1011-100 | 14.5 | 16 de noviembre de 1970 |
| DC-10-40 | 13.8 | 29 de agosto de 1970 |
| A300-600 | 15.2 | 28 de octubre de 1972 |
| MD-11 | 16.1 | 10 de enero de 1990 |
| B767-200ER | 16.1 | 26 de septiembre de 1981 |
| A310-300 | 15.3 | Apr 3, 1982 |
| B747-200 | 15.3 | 9 de febrero de 1969 |
| B747-400 | 15,5 | 29 de abril de 1988 |
| B757-200 | 15.0 | 19 de febrero de 1982 |
| A320-200 | 16.3 | 22 de febrero de 1987 |
| A310-300 | 18.1 | 2 de noviembre de 1992 |
| A340-200 | 19.2 | 1o de abril de 1992 |
| A340-300 | 19.1 | 25 de octubre de 1991 |
| B777-200 | 19.3 | 12 de junio de 1994 |
Contenido relacionado
Histograma de color
El engaño del coeficiente intelectual presidencial de EE. UU.
Van der Waals










