Refracción atmosférica

La refracción atmosférica es la desviación de la luz u otra onda electromagnética de una línea recta a su paso por la atmósfera debido a la variación de la densidad del aire en función de la altura. Esta refracción se debe a que la velocidad de la luz a través del aire disminuye (el índice de refracción aumenta) al aumentar la densidad. La refracción atmosférica cerca del suelo produce espejismos. Tal refracción también puede elevar o disminuir, estirar o acortar las imágenes de objetos distantes sin involucrar espejismos. El aire turbulento puede hacer que los objetos distantes parezcan parpadear o brillar. El término también se aplica a la refracción del sonido. La refracción atmosférica se considera al medir la posición de objetos celestes y terrestres.

La refracción astronómica o celeste hace que los objetos astronómicos parezcan más altos sobre el horizonte de lo que realmente están. La refracción terrestre generalmente hace que los objetos terrestres parezcan más altos de lo que realmente son, aunque por la tarde, cuando el aire cerca del suelo se calienta, los rayos pueden curvarse hacia arriba haciendo que los objetos parezcan más bajos de lo que realmente son.

La refracción no sólo afecta a los rayos de luz visible, sino a toda la radiación electromagnética, aunque en distintos grados. Por ejemplo, en el espectro visible, el azul se ve más afectado que el rojo. Esto puede hacer que los objetos astronómicos aparezcan dispersos en un espectro en imágenes de alta resolución.

Siempre que sea posible, los astrónomos programarán sus observaciones alrededor de los momentos de culminación, cuando los objetos celestes están más altos en el cielo. Asimismo, los marineros no dispararán a una estrella a menos de 20° sobre el horizonte. Si no se pueden evitar las observaciones de objetos cercanos al horizonte, es posible equipar un telescopio óptico con sistemas de control para compensar el desplazamiento causado por la refracción. Si la dispersión también es un problema (en el caso de observaciones de alta resolución de banda ancha), también se pueden emplear correctores de refracción atmosférica (fabricados con pares de prismas de vidrio giratorios).

Dado que la cantidad de refracción atmosférica es función del gradiente de temperatura, la temperatura, la presión y la humedad (la cantidad de vapor de agua, que es especialmente importante en longitudes de onda del infrarrojo medio), la cantidad de esfuerzo necesario para una compensación exitosa puede resultar prohibitivo. Los topógrafos, por otro lado, suelen programar sus observaciones por la tarde, cuando la magnitud de la refracción es mínima.

La refracción atmosférica se vuelve más severa cuando los gradientes de temperatura son fuertes y la refracción no es uniforme cuando la atmósfera es heterogénea, como cuando ocurre turbulencia en el aire. Esto provoca condiciones de visión subóptimas, como el centelleo de las estrellas y diversas deformaciones de la forma aparente del Sol poco antes del atardecer o después del amanecer.

Refracción astronómica

La refracción astronómica se ocupa de la posición angular de los cuerpos celestes, su apariencia como fuente puntual y, a través de la refracción diferencial, la forma de cuerpos extendidos como el Sol y la Luna.

La refracción atmosférica de la luz de una estrella es cero en el cenit, menos de 1′ (un minuto de arco) a 45° de altitud aparente, y todavía sólo 5,3′ a 10° de altitud; aumenta rápidamente a medida que disminuye la altitud, alcanzando 9,9′ a 5° de altitud, 18,4′ a 2° de altitud y 35,4′ en el horizonte; todos los valores son para 10 °C y 1013,25 hPa en la parte visible del espectro.

En el horizonte, la refracción es ligeramente mayor que el diámetro aparente del Sol, por lo que cuando la parte inferior del disco solar parece tocar el horizonte, la verdadera altitud del Sol es negativa. Si la atmósfera desapareciera repentinamente en ese momento, no se podría ver el sol, ya que estaría completamente debajo del horizonte. Por convención, la salida y la puesta del sol se refieren a los momentos en que el extremo superior del Sol aparece o desaparece del horizonte y el valor estándar para la altitud verdadera del Sol es −50′: −34′ para la refracción. y −16′ para el semidiámetro del Sol. La altitud de un cuerpo celeste normalmente se da para el centro del disco del cuerpo. En el caso de la Luna, se necesitan correcciones adicionales para el paralaje horizontal de la Luna y su semidiámetro aparente; ambos varían con la distancia Tierra-Luna.

La refracción cerca del horizonte es muy variable, principalmente debido a la variabilidad del gradiente de temperatura cerca de la superficie de la Tierra y la sensibilidad geométrica de los rayos casi horizontales a esta variabilidad. Ya en 1830, Friedrich Bessel había descubierto que incluso después de aplicar todas las correcciones de temperatura y presión (pero no del gradiente de temperatura) al observador, mediciones muy precisas de refracción variaban en ±0,19′ a dos grados sobre el horizonte y en ±0,19′ a dos grados sobre el horizonte y en ± 0,50′ a medio grado sobre el horizonte. En el horizonte y debajo de él, se han observado valores de refracción significativamente superiores al valor nominal de 35,4′ en una amplia gama de climas. Georg Constantin Bouris midió una refracción de hasta 4° para las estrellas en el horizonte en el Observatorio de Atenas y, durante su desafortunada expedición Endurance, Sir Ernest Shackleton registró una refracción de 2°37′:

“El sol que había hecho 'definitivamente su última aparición' siete días antes nos sorprendió al levantar más de la mitad de su disco sobre el horizonte el 8 de mayo. Un resplandor en el horizonte norte se convirtió en el sol a las 11 am de ese día. . Un cuarto de hora más tarde, el visitante irracional volvió a desaparecer, sólo para levantarse de nuevo a las 11:40, fijarse a las 13:00, levantarse a las 13:10 y desaparecer lentamente a las 13:20. Estos curiosos fenómenos se debieron a una refracción que ascendió a 2° 37′ a las 13:20 horas. La temperatura era 15° por debajo de 0° Fahr., y calculamos que la refracción estaba 2° por encima de lo normal”.

Las variaciones meteorológicas de un día a otro afectarán a las horas exactas de salida y puesta del sol, así como a la salida y puesta de la luna, y por esa razón, generalmente no tiene sentido indicar las horas de salida y puesta con mayor precisión. que el minuto más cercano. Cálculos más precisos pueden ser útiles para determinar los cambios diarios en los tiempos de subida y bajada que ocurrirían con el valor estándar de refracción si se entiende que los cambios reales pueden diferir debido a variaciones impredecibles en la refracción.

Debido a que la refracción atmosférica es nominalmente de 34′ en el horizonte, pero sólo de 29′ a 0,5° por encima de él, el sol poniente o naciente parece estar aplanado aproximadamente 5′ (aproximadamente 1/6 de su diámetro aparente).

Calcular la refracción

Young distinguió varias regiones donde eran aplicables diferentes métodos para calcular la refracción astronómica. En la parte superior del cielo, con una distancia cenital inferior a 70° (o una altitud superior a 20°), varias fórmulas de refracción simples basadas en el índice de refracción (y por tanto en la temperatura, presión y humedad) en el observador son adecuados. Entre 20° y 5° del horizonte, el gradiente de temperatura se convierte en el factor dominante y se requiere la integración numérica, utilizando un método como el de Auer y Standish y empleando el gradiente de temperatura de la atmósfera estándar y las condiciones medidas en el observador. Más cerca del horizonte, es necesario emplear en la integración numérica mediciones reales de los cambios con la altura del gradiente de temperatura local. Debajo del horizonte astronómico, la refracción es tan variable que sólo se pueden hacer estimaciones aproximadas de la refracción astronómica; por ejemplo, la hora observada de salida o puesta del sol puede variar varios minutos de un día a otro. Como señala The Nautical Almanac, "los valores reales de... la refracción a bajas altitudes pueden, en condiciones atmosféricas extremas, diferir considerablemente de los valores medios utilizados en las tablas".

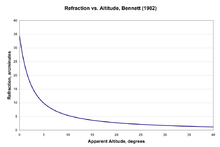
Se han desarrollado muchas fórmulas diferentes para calcular la refracción astronómica; son razonablemente consistentes, difieren entre sí en unos pocos minutos de arco en el horizonte y se vuelven cada vez más consistentes a medida que se acercan al cenit. Las formulaciones más simples implicaban nada más que la temperatura y la presión en el observador, potencias de la cotangente de la altitud aparente del cuerpo astronómico y, en términos de orden superior, la altura de una atmósfera homogénea ficticia. La versión más simple de esta fórmula, que según Smart sólo era precisa dentro de los 45° del cenit, es:

R=()n0− − 1)cot⁡ ⁡ ha,{displaystyle R=(n_{0}-1)cot h_{mathrm {a},}

donde R es la refracción en radianes, n₀ es el índice de refracción en el observador (que depende de la temperatura, presión , y humedad), y h_a es el ángulo de altitud aparente del cuerpo astronómico.

George Comstock desarrolló una primera aproximación simple de esta forma, que incorporaba directamente la temperatura y la presión en el observador:

R=21.5b273+tcot⁡ ⁡ ha,{displaystyle R={frac {21.5b}{273+t}cot h_{mathrm {a},}

donde R es la refracción en segundos de arco, b es la presión atmosférica en milímetros de mercurio y t es la temperatura en Celsius. Comstock consideró que esta fórmula daba resultados dentro de un segundo de arco de los valores de Bessel para la refracción desde 15° sobre el horizonte hasta el cenit.

Una mayor expansión en términos de la tercera potencia de la cotangente de la altitud aparente incorpora H₀, la altura de la atmósfera homogénea, además de las condiciones habituales al observador:

R=()n0− − 1)()1− − H0)cot⁡ ⁡ ha− − ()n0− − 1)[H0− − 12()n0− − 1)]cot3⁡ ⁡ ha.{displaystyle R=(n_{0}-1)(1-H_{0})cot h_{mathrm {a}-(n_{0}-1)[H_{0}-{0}{2} {0}(n_{0}-1)]

Se utiliza una versión de esta fórmula en los Estándares de Astronomía Fundamental de la Unión Astronómica Internacional; una comparación del algoritmo de la IAU con procedimientos de trazado de rayos más rigurosos indicó una concordancia dentro de 60 milisegundos de arco en altitudes superiores a 15°.

Bennett desarrolló otra fórmula empírica simple para calcular la refracción a partir de la altitud aparente que da la refracción R en minutos de arco:

R=cot⁡ ⁡ ()ha+7.31ha+4.4).{displaystyle R=cot left(h_{mathrm {a}+{frac {7.31}{h_{mathrm {a} }+4}right),}

Esta fórmula se utiliza en el Observatorio Naval de EE.UU. Vector Astrometry Software, y se reporta que es consistente con el algoritmo más complejo de Garfinkel dentro de 0.07′ sobre todo el rango desde el cenit hasta el horizonte. Sæmundsson desarrolló una fórmula inversa para determinar la refracción de verdadero altitud; si h es la verdadera altitud en grados, refracción R en arcminutes es dado por

R=1.02cot⁡ ⁡ ()h+10.3h+5.11);{displaystyle R=1.02cot left(h+{frac {10.3}{h+5.11}right);}

la fórmula es consistente con la de Bennett con una precisión de 0,1′. Las fórmulas de Bennet y Sæmundsson suponen una presión atmosférica de 101,0 kPa y una temperatura de 10 °C; para diferentes presiones P y temperaturas T, la refracción calculada a partir de estas fórmulas se multiplica por

P101283273+T{displaystyle {frac {f}},{frac {283}{273+T}}

La refracción aumenta aproximadamente un 1 % por cada aumento de presión de 0,9 kPa y disminuye aproximadamente un 1 % por cada disminución de presión de 0,9 kPa. De manera similar, la refracción aumenta aproximadamente un 1% por cada 3 °C de disminución de temperatura y disminuye aproximadamente un 1% por cada 3 °C de aumento de temperatura.

Efectos de refracción aleatoria

La turbulencia en la atmósfera de la Tierra dispersa la luz de las estrellas, haciéndolas parecer más brillantes y más débiles en una escala de tiempo de milisegundos. Los componentes más lentos de estas fluctuaciones son visibles como centelleos (también llamados centelleo).

La turbulencia también provoca pequeños movimientos esporádicos de la imagen de la estrella y produce rápidas distorsiones en su estructura. Estos efectos no son visibles a simple vista, pero pueden verse fácilmente incluso con telescopios pequeños. Perturban las condiciones de visión astronómica. Algunos telescopios emplean óptica adaptativa para reducir este efecto.

Refracción terrestre

refracción terrestre, a veces llamada refracción geodésica, se ocupa de la posición angular aparente y la distancia medida de los cuerpos terrestres. Es de especial interés para la producción de mapas y estudios precisos. Dado que la línea de visión en la refracción terrestre pasa cerca de la superficie terrestre, la magnitud de la refracción depende principalmente del gradiente de temperatura cerca del suelo, que varía ampliamente en diferentes momentos del día, estaciones del año, la naturaleza del terreno, el estado del tiempo y otros factores.

Como aproximación común, la refracción terrestre se considera como una curvatura constante del rayo de luz o de la línea de visión, en la que se puede considerar que el rayo describe una trayectoria circular. Una medida común de refracción es el coeficiente de refracción. Desafortunadamente existen dos definiciones diferentes de este coeficiente. Uno es la relación entre el radio de la Tierra y el radio de la línea de visión, el otro es la relación entre el ángulo que la línea de visión subtiende en el centro de la Tierra y el ángulo de refracción medido por el observador. Dado que la última definición sólo mide la curvatura del rayo en un extremo de la línea de visión, es la mitad del valor de la definición anterior.

El coeficiente de refracción está directamente relacionado con el gradiente de temperatura vertical local y la temperatura y presión atmosférica. La versión más grande del coeficiente k, que mide la relación entre el radio de la Tierra y el radio de la línea de visión, viene dada por:

k=503PT2()0,0343+dTdh),{displaystyle k=503{frac {fnK}}left(0.0343+{frac {dT}right),}

donde la temperatura T se da en kelvins, la presión P en milibares y la altura h en metros. El ángulo de refracción aumenta con el coeficiente de refracción y con la longitud de la línea de visión.

Aunque la línea recta desde el ojo hasta una montaña distante puede estar bloqueada por una colina más cercana, el rayo puede curvarse lo suficiente como para hacer visible el pico distante. Un método conveniente para analizar el efecto de la refracción en la visibilidad es considerar un radio efectivo aumentado de la Tierra R_eff, dado por

Reff=R1− − k,{displaystyle ¿Qué? {R}{1-k},}

Donde R es el radio de la Tierra y k es el coeficiente de refracción. Bajo este modelo, el rayo puede considerarse una línea recta en una Tierra de mayor radio.

La curvatura del rayo refractado en segundos de arco por metro se puede calcular usando la relación

1σ σ =16.3PT2()0,0342+dTdh)#⁡ ⁡ β β {displaystyle {frac}{sigma }=16.3{frac {P}{2}}left(0.0342+{frac {dT}right)cos beta }

donde 1/σ es la curvatura del rayo en segundos de arco por metro, P es la presión en milibares, T es la temperatura en kelvins y β es la ángulo del rayo con la horizontal. Multiplicar la mitad de la curvatura por la longitud de la trayectoria del rayo da el ángulo de refracción en el observador. Para una línea de visión cerca del horizonte, cos β difiere poco de la unidad y puede ignorarse. Esto produce

Ω Ω =8.15LPT2()0,0342+dTdh),{displaystyle Omega =8.15{frac {LP} {T^{2}}left(0.0342+{frac {dT}{dh}}right),}

donde L es la longitud de la línea de visión en metros y Ω es la refracción en el observador medida en segundos de arco.

Una aproximación simple es considerar que la altitud aparente de una montaña a la vista (en grados) excederá su altitud real por su distancia en kilómetros dividida por 1500. Esto supone una línea de visión bastante horizontal y aire ordinario. densidad; si la montaña es muy alta (gran parte de la línea de visión está en el aire menos espesa), divida entre 1600.