Red distributiva

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En matemáticas, una red distributiva es una red en la que las operaciones de unir y encontrar se distribuyen entre sí. Los ejemplos prototípicos de tales estructuras son colecciones de conjuntos para los cuales las operaciones de celosía se pueden dar mediante la unión y la intersección de conjuntos. De hecho, estos retículos de conjuntos describen completamente el paisaje: cada retículo distributivo se da —salvo el isomorfismo— como tal retículo de conjuntos.

Definición

Como en el caso de los retículos arbitrarios, uno puede optar por considerar un retículo distributivo L ya sea como una estructura de teoría del orden o de álgebra universal. Ambos puntos de vista y su correspondencia mutua se discuten en el artículo sobre celosías. En la situación actual, la descripción algebraica parece ser más conveniente.

Una red (L,∨,∧) es distributiva si la siguiente identidad adicional se cumple para todas las x, y y z en L:

x ∧Sí. Alternativa z) =x ∧ Sí.) ∨x ∧ z).

Al ver los retículos como conjuntos parcialmente ordenados, esto indica que la operación de reunión conserva uniones finitas no vacías. Es un hecho básico de la teoría de la red que la condición anterior es equivalente a su dual:

x AlternativaSí. ∧ z) =x Alternativa Sí.∧x Alternativa z) para todos x, Sí., y z dentro L.

En cada celosía, definiendo p≤q como de costumbre para significar p∧q= p, la desigualdad x ∧ (y ∨ z) ≥ (x ∧ y) ∨ (x ∧ z) se cumple tan bien como su desigualdad dual x ∨ (y ∧ z) ≤ (x ∨ y) ∧ (x ∨ z). Una red es distributiva si también se cumple una de las desigualdades inversas. Se puede encontrar más información sobre la relación de esta condición con otras condiciones de distributividad de la teoría del orden en el artículo sobre distributividad (teoría del orden).

Morfismos

Un morfismo de retículos distributivos es simplemente un homomorfismo de retículos como se indica en el artículo sobre retículos, es decir, una función que es compatible con las dos operaciones de retículos. Debido a que tal morfismo de retículas conserva la estructura de la retícula, en consecuencia también preservará la distributividad (y por lo tanto será un morfismo de retículas distributivas).

Ejemplos

Las redes distributivas son estructuras ubicuas pero también bastante específicas. Como ya se mencionó, el principal ejemplo de retículas distributivas son las retículas de conjuntos, donde la unión y el encuentro están dados por las operaciones habituales de la teoría de conjuntos. Otros ejemplos incluyen:

El álgebra Lindenbaum de la mayoría de las lógicas que soportan la conjunción y la disyunción es una celosía distributiva, es decir, "y" distribuye sobre "o" y viceversa.
Cada álgebra booleana es una celosía distributiva.
Cada álgebra Heyting es una celosía distributiva. Especialmente esto incluye todos los locales y por lo tanto todas las vestiduras abiertas de los espacios topológicos. También note que los álgebras Heyting se pueden ver como álgebras Lindenbaum de la lógica intuitionista, que los hace un caso especial del primer ejemplo.
Cada conjunto totalmente ordenado es una celosa distributiva con máx como unirse y min como conocer.
Los números naturales forman una celosía distributiva (condicionalmente completa) tomando el mayor divisor común como reunión y el múltiplo menos común como unión. Esta celosía también tiene un elemento mínimo, a saber, 1, que por lo tanto sirve como elemento de identidad para las uniones.
Dado un entero positivo n, el conjunto de todos los divisores positivos n forma una celosía distributiva, de nuevo con el mayor divisor común como encuentro y el más común múltiple como unirse. Este es un álgebra booleana si y sólo si n es libre de cuadrados.
Un espacio vectorial de celosía es una celosía distributiva.
La vestimenta de Young dada por la inclusión ordenando los diagramas Young representando particiones enteros es una celosía distributiva.
Los puntos de un politopo distributivo (un politopo convexo cerrado bajo mínimo coordenado y operaciones máximas coordinadas), con estas dos operaciones como la unión y las operaciones de la celosía.

Al principio del desarrollo de la teoría del entramado, Charles S. Peirce creía que todos los entramados son distributivos, es decir, la distributividad se deriva del resto de los axiomas del entramado. Sin embargo, las pruebas de independencia fueron dadas por Schröder, Voigt, ^(de) Lüroth, Korselt y Dedekind.

Propiedades características

Existen varias formulaciones equivalentes a la definición anterior. Por ejemplo, L es distributivo si y solo si lo siguiente se cumple para todos los elementos x, y, z en L:

()x

wedge

Sí.)

vee

()Sí.

wedge

vee

()z

wedge

x) =x

vee

Sí.)

wedge

()Sí.

vee

wedge

()z

vee

x).

Del mismo modo, L es distributivo si y solo si

wedge

z = Sí.

wedge

z y x

vee

z = Sí.

vee

z siempre implicado x=Sí..

Diagramas de Hasse de las dos tratecciones prototípicas no distributivas
El traje de diamante M₃ no es distributivo: x ∧Sí. Alternativa z) = x ∧ 1 = x √≥ 0 = 0 ∨ 0 = ()x ∧ Sí.) ∨x ∧ z).
La vestimenta del Pentágono N₅ no es distributivo: x ∧Sí. Alternativa z) = x ∧ 1 = x ل z = 0 z = ()x ∧ Sí.) ∨x ∧ z).

Las redes no distributivas más simples son M₃, la "red de diamantes" y N ₅, la "red del pentágono". Una red es distributiva si y solo si ninguna de sus subredes es isomorfa a M₃ o N₅; una subred es un subconjunto que se cierra bajo las operaciones de encuentro y unión de la red original. Tenga en cuenta que esto no es lo mismo que ser un subconjunto que es una red en el orden original (pero posiblemente con diferentes operaciones de unión y reunión). Otras caracterizaciones se derivan de la teoría de la representación en la siguiente sección.

Una forma alternativa de afirmar el mismo hecho es que todo retículo distributivo es un producto subdirecto de copias de la cadena de dos elementos, o que el único miembro subdirectamente irreducible de la clase de retículos distributivos es la cadena de dos elementos. Como corolario, toda red booleana también tiene esta propiedad.

Finalmente, la distributividad implica varias otras propiedades agradables. Por ejemplo, un elemento de un retículo distributivo es primo si y solo si es irreducible, aunque esta última es en general una propiedad más débil. Por dualidad, lo mismo es cierto para los elementos unidos-primos y unidos-irreducibles. Si una red es distributiva, su relación de cobertura forma un gráfico mediano.

Además, cada red distributiva también es modular.

Teoría de la representación

La introducción ya insinuó la caracterización más importante de los retículos distributivos: un retículo es distributivo si y solo si es isomorfo a un retículo de conjuntos (cerrado bajo unión e intersección de conjuntos). (La última estructura a veces se denomina anillo de conjuntos en este contexto.) Que la unión y la intersección de conjuntos sean realmente distributivas en el sentido anterior es un hecho elemental. La otra dirección es menos trivial, ya que requiere los teoremas de representación que se indican a continuación. La idea importante de esta caracterización es que las identidades (ecuaciones) que se cumplen en todos los retículos distributivos son exactamente las mismas que se cumplen en todos los retículos de conjuntos en el sentido anterior.

El teorema de representación de Birkhoff para retículas distributivas establece que cada retícula distributiva finita es isomorfa a la retícula de los conjuntos inferiores del conjunto de sus elementos primos unidos (equivalentemente: elementos irreducibles unidos). Esto establece una biyección (hasta el isomorfismo) entre la clase de todos los posets finitos y la clase de todos los retículos distributivos finitos. Esta biyección se puede extender a una dualidad de categorías entre homomorfismos de redes distributivas finitas y funciones monótonas de posets finitas. Sin embargo, generalizar este resultado a redes infinitas requiere agregar una estructura adicional.

Otro de los primeros teoremas de representación ahora se conoce como teorema de representación de Stone para redes distributivas (el nombre honra a Marshall Harvey Stone, quien lo demostró por primera vez). Caracteriza los retículos distributivos como los retículos de conjuntos abiertos compactos de ciertos espacios topológicos. Este resultado puede verse como una generalización del famoso teorema de representación de Stone para álgebras booleanas y como una especialización del escenario general de la dualidad de Stone.

Hilary Priestley estableció otra representación importante en su teorema de representación para redes distributivas. En esta formulación, se utiliza una red distributiva para construir un espacio topológico con un orden parcial adicional en sus puntos, lo que produce un espacio de Stone ordenado (completamente separado por orden) (o espacio de Priestley). Se recupera la celosía original como el conjunto de conjuntos inferiores abiertos de este espacio.

Como consecuencia de los teoremas de Stone y Priestley, uno ve fácilmente que cualquier red distributiva es realmente isomorfa a una red de conjuntos. Sin embargo, las pruebas de ambas afirmaciones requieren el teorema del ideal primo booleano, una forma débil del axioma de elección.

Redes distributivas libres

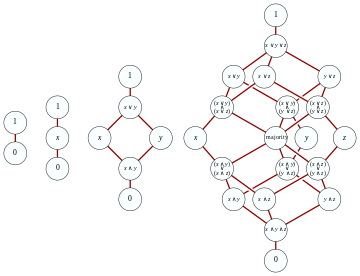
La rejilla distributiva gratuita sobre un conjunto de generadores G se puede construir mucho más fácilmente que una ropa libre general. La primera observación es que, utilizando las leyes de distribución, cada término formado por las operaciones binarias $lor$ y $land$ en un conjunto de generadores se puede transformar en el equivalente siguiente forma normal:

{displaystyle M_{1}lor M_{2}lor cdots lor M_{n},}

Donde $M_{i}$ son encuentros finitos de elementos de G. Además, ya que ambos se reúnen y se unen son asociativos, comunicativos e idempotentes, se puede ignorar los duplicados y el orden, y representar una unión de reuniones como la anterior como un conjunto de conjuntos:

{displaystyle {N_{1},N_{2},ldotsN_{n}},}

Donde $N_{i}$ son subconjuntos finitos de G. Sin embargo, es posible que dos de esos términos denotan el mismo elemento de la celosía distributiva. Esto ocurre cuando hay índices j y k tales que $N_{j}$ es un subconjunto de ${displaystyle N_{k}.}$ En este caso la reunión de $N_{k}$ estará por debajo de la reunión ${displaystyle N_{j},}$ y por lo tanto uno puede quitar con seguridad redundante redundante set $N_{k}$ sin cambiar la interpretación de todo el término. En consecuencia, un conjunto de subconjuntos finitos de G será llamado irredundant cuando todos sus elementos $N_{i}$ son mutuamente incomparables (con respecto al orden del subconjunto); es decir, cuando forma un antichain de conjuntos finitos.

Ahora la rejilla distributiva gratuita sobre un conjunto de generadores G se define en el conjunto de todos los conjuntos finitos irredundantes de subconjuntos finitos de G. La unión de dos conjuntos de irredundantes finitos se obtiene de su unión eliminando todos los conjuntos redundantes. Del mismo modo el encuentro de dos sets S y T es la versión irredundante de ${displaystyle {Ncup Mmid Nin S,Min T}.}$ La verificación de que esta estructura es una celosía distributiva con la propiedad universal requerida es rutinaria.

El número de elementos en redes distributivas libres con generadores n viene dado por los números de Dedekind. Estos números crecen rápidamente y solo se conocen para n ≤ 9; ellos son

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788, 286386577668298411128469151667598498812366 A000372 en el OEIS).

Los números anteriores cuentan el número de elementos en retículas distributivas libres en las que las operaciones de retícula son uniones y encuentros de conjuntos finitos de elementos, incluido el conjunto vacío. Si no se permiten uniones vacías ni encuentros vacíos, los retículos distributivos libres resultantes tienen dos elementos menos; sus números de elementos forman la secuencia

0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 56130437228687557907786, 286386577668298411128469151667598498812364 A007153 en el OEIS).

Contenido relacionado

Más resultados...