Recursividad (computación)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En informática, recursividad o recursión es un método para resolver un problema computacional donde la solución depende de soluciones a instancias más pequeñas del mismo problema. La recursividad resuelve tales problemas recursivos mediante el uso de funciones que se llaman a sí mismas desde su propio código. El enfoque se puede aplicar a muchos tipos de problemas, y la recursividad es una de las ideas centrales de la informática.

Evidentemente, el poder de la recursividad reside en la posibilidad de definir un conjunto infinito de objetos mediante un enunciado finito. De la misma manera, un programa recursivo finito puede describir un número infinito de cálculos, incluso si este programa no contiene repeticiones explícitas.

— Niklaus Wirth, Algoritmos + Estructuras de datos = Programas , 1976

La mayoría de los lenguajes de programación de computadoras admiten la recursividad al permitir que una función se llame a sí misma desde su propio código. Algunos lenguajes de programación funcionales (por ejemplo, Clojure) no definen ninguna construcción de bucle, sino que se basan únicamente en la recursividad para llamar repetidamente al código. Está demostrado en la teoría de la computabilidad que estos lenguajes solo recursivos son Turing completos; esto significa que son tan poderosos (pueden usarse para resolver los mismos problemas) como lenguajes imperativos basados en estructuras de control como whiley for.

Llamar repetidamente a una función desde dentro de sí misma puede hacer que la pila de llamadas tenga un tamaño igual a la suma de los tamaños de entrada de todas las llamadas involucradas. De ello se deduce que, para problemas que pueden resolverse fácilmente mediante iteración, la recursividad es generalmente menos eficiente y, para problemas grandes, es fundamental utilizar técnicas de optimización como la optimización de llamada de cola.

Funciones y algoritmos recursivos

Una táctica común de diseño de algoritmos es dividir un problema en subproblemas del mismo tipo que el original, resolver esos subproblemas y combinar los resultados. Esto a menudo se conoce como el método divide y vencerás; cuando se combina con una tabla de búsqueda que almacena los resultados de los subproblemas resueltos previamente (para evitar resolverlos repetidamente e incurrir en tiempo de cálculo adicional), puede denominarse programación dinámica o memorización.

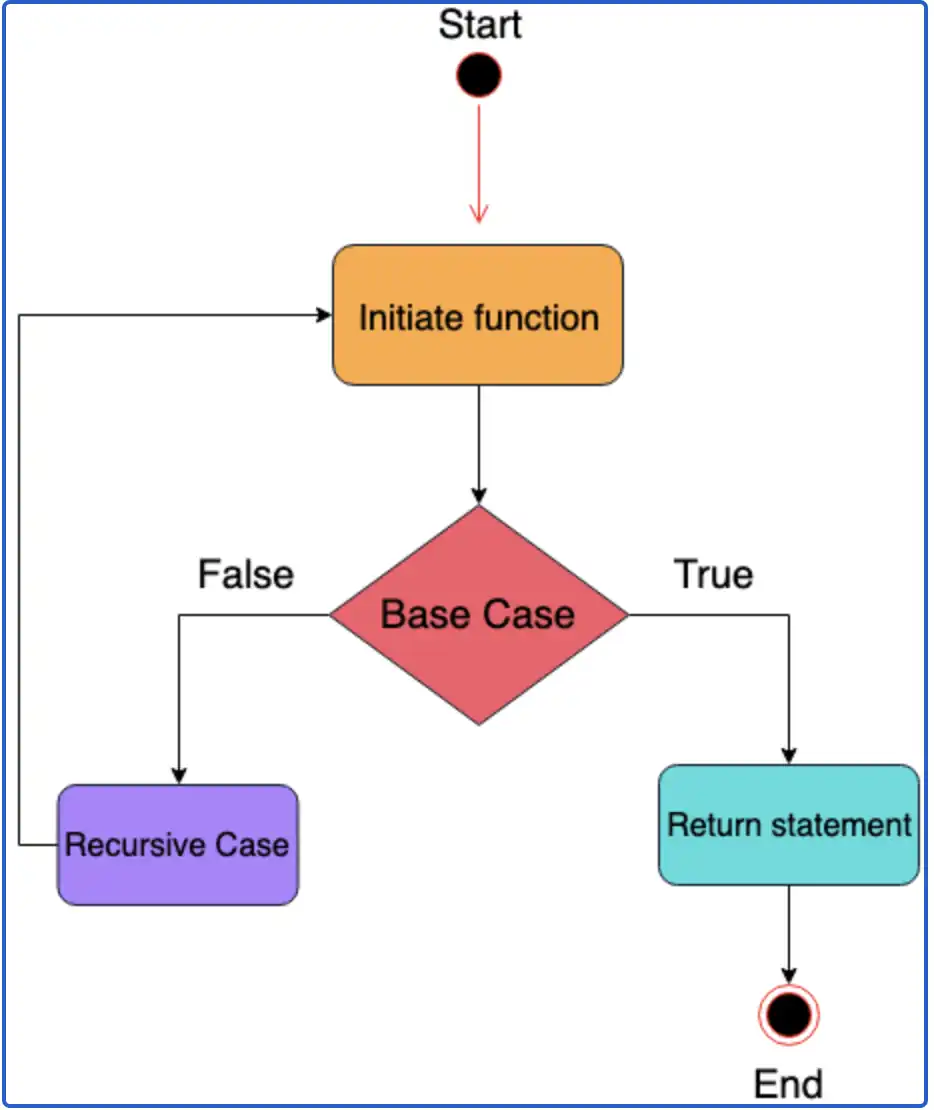
Caso base

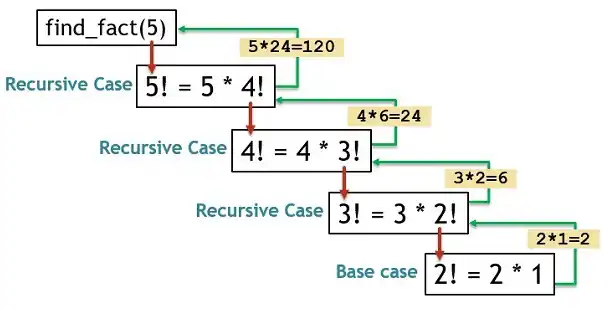
Una definición de función recursiva tiene uno o más casos base, es decir, entradas para las cuales la función produce un resultado de forma trivial (sin recurrencia), y uno o más casos recursivos, es decir, entradas para las cuales el programa recurre (se llama a sí mismo). Por ejemplo, la función factorial se puede definir recursivamente mediante las ecuaciones 0! = 1 y, para todo n > 0, n ! = norte (norte - 1)!. Ninguna ecuación por sí misma constituye una definición completa; el primero es el caso base y el segundo es el caso recursivo. Debido a que el caso base rompe la cadena de recursividad, a veces también se le llama "caso final".

El trabajo de los casos recursivos puede verse como descomponer entradas complejas en otras más simples. En una función recursiva correctamente diseñada, con cada llamada recursiva, el problema de entrada debe simplificarse de tal manera que finalmente se debe llegar al caso base. (Las funciones que no están destinadas a terminar en circunstancias normales, por ejemplo, algunos procesos del sistema y del servidor, son una excepción a esto). Omitir escribir un caso base o probarlo incorrectamente puede causar un bucle infinito.

Para algunas funciones (como una que calcula la serie para e = 1/0! + 1/1! + 1/2! + 1/3! +...) no hay un caso base obvio implícito en los datos de entrada; para estos, se puede agregar un parámetro (como el número de términos que se agregarán, en nuestro ejemplo de serie) para proporcionar un 'criterio de finalización' que establece el caso base. Este ejemplo se trata de forma más natural mediante la correcursión, donde los términos sucesivos de la salida son las sumas parciales; esto se puede convertir en una recursividad usando el parámetro de indexación para decir "calcular el n -ésimo término (la n -ésima suma parcial)".

Tipos de datos recursivos

Muchos programas de computadora deben procesar o generar una cantidad arbitrariamente grande de datos. La recursividad es una técnica para representar datos cuyo tamaño exacto es desconocido para el programador: el programador puede especificar estos datos con una definición autorreferencial. Hay dos tipos de definiciones autorreferenciales: definiciones inductivas y coinductivas.

Datos definidos inductivamente

Una definición de datos recursivos definida inductivamente es aquella que especifica cómo construir instancias de los datos. Por ejemplo, las listas enlazadas se pueden definir de forma inductiva (aquí, usando la sintaxis de Haskell):

datos  ListOfStrings  =  ListaVacía  |  Contras  Cadena  ListOfStrings

El código anterior especifica que una lista de cadenas esté vacía o una estructura que contenga una cadena y una lista de cadenas. La autorreferencia en la definición permite la construcción de listas de cualquier número (finito) de cadenas.

Otro ejemplo de definición inductiva son los números naturales (o enteros positivos):

Un número natural es 1 o n+1, donde n es un número natural.

De manera similar, las definiciones recursivas se usan a menudo para modelar la estructura de expresiones y declaraciones en lenguajes de programación. Los diseñadores de idiomas a menudo expresan gramáticas en una sintaxis como la forma Backus-Naur; aquí hay una gramática de este tipo, para un lenguaje simple de expresiones aritméticas con multiplicación y suma:

 < expr >::=  < número > 
          | (< expr > * < expr >)
          | (< expresión > + < expresión >)

Esto dice que una expresión es un número, un producto de dos expresiones o una suma de dos expresiones. Al referirse recursivamente a expresiones en la segunda y tercera línea, la gramática permite expresiones aritméticas arbitrariamente complicadas como (5 * ((3 * 6) + 8)), con más de una operación de producto o suma en una sola expresión.

Datos definidos de forma coincidente y correcursión

Una definición de datos coinductivos es aquella que especifica las operaciones que se pueden realizar en un dato; por lo general, las definiciones coinductivas autorreferenciales se utilizan para estructuras de datos de tamaño infinito.

Una definición coinductiva de flujos infinitos de cadenas, dada de manera informal, podría verse así:

Un flujo de cadenas es un objeto tal que:
 head(s) es una cadena, y
 tail(s) es un flujo de cadenas.

Esto es muy similar a una definición inductiva de listas de cadenas; la diferencia es que esta definición especifica cómo acceder a los contenidos de la estructura de datos, es decir, a través de las funciones de acceso heady tailcuáles pueden ser esos contenidos, mientras que la definición inductiva especifica cómo crear la estructura y de qué se puede crear.

La correcursión está relacionada con la coinducción y se puede usar para calcular instancias particulares de (posiblemente) objetos infinitos. Como técnica de programación, se usa con mayor frecuencia en el contexto de lenguajes de programación perezosos y puede ser preferible a la recursividad cuando se desconoce el tamaño o la precisión deseados de la salida de un programa. En tales casos, el programa requiere tanto una definición para un resultado infinitamente grande (o infinitamente preciso) como un mecanismo para tomar una porción finita de ese resultado. El problema de calcular los primeros n números primos se puede resolver con un programa correcursivo (por ejemplo, aquí).

Tipos de recursividad

Recurrencia única y recursión múltiple

La recursividad que contiene una sola autorreferencia se conoce comorecursión única, mientras que la recursión que contiene múltiples autorreferencias se conoce comorecursión múltiple. Los ejemplos estándar de recursividad única incluyen el recorrido de listas, como en una búsqueda lineal, o el cálculo de la función factorial, mientras que los ejemplos estándar de recursividad múltiple incluyen el recorrido de árboles, como en una búsqueda en profundidad.

La recursión única suele ser mucho más eficiente que la recursión múltiple y, en general, puede reemplazarse por un cálculo iterativo, que se ejecuta en tiempo lineal y requiere un espacio constante. La recursión múltiple, por el contrario, puede requerir tiempo y espacio exponenciales, y es más fundamentalmente recursiva, ya que no puede ser reemplazada por iteración sin una pila explícita.

A veces, la recursividad múltiple se puede convertir en recursividad única (y, si se desea, de ahí en iteración). Por ejemplo, mientras que calcular la secuencia de Fibonacci implica ingenuamente múltiples iteraciones, ya que cada valor requiere dos valores previos, se puede calcular mediante una sola recursión pasando dos valores sucesivos como parámetros. Esto se enmarca de manera más natural como correcursión, que se construye a partir de los valores iniciales, mientras se rastrean dos valores sucesivos en cada paso; consulte corecursión: ejemplos. Un ejemplo más sofisticado implica el uso de un árbol binario con subprocesos, que permite el recorrido iterativo del árbol, en lugar de la recursividad múltiple.

Recursividad indirecta

La mayoría de los ejemplos básicos de recursión, y la mayoría de los ejemplos presentados aquí, demuestranrecursividad directa, en la que una función se llama a sí misma. La recursión indirecta ocurre cuando una función no es llamada por sí misma sino por otra función a la que llamó (ya sea directa o indirectamente). Por ejemplo, si f llama a f, eso es recursión directa, pero si f llama a g que llama a f, entonces eso es recursión indirecta de f. Son posibles cadenas de tres o más funciones; por ejemplo, la función 1 llama a la función 2, la función 2 llama a la función 3 y la función 3 llama a la función 1 nuevamente.

La recursión indirecta también se llama recursión mutua, que es un término más simétrico, aunque esto es simplemente una diferencia de énfasis, no una noción diferente. Es decir, si f llama a g y luego g llama a f, que a su vez llama a g nuevamente, desde el punto de vista de f solo, f es indirectamente recurrente, mientras que desde el punto de vista de g solo, es indirectamente recurrente, mientras que desde el punto de vista de ambos, f y g son mutuamente recurrentes entre sí. De manera similar, un conjunto de tres o más funciones que se llaman entre sí puede llamarse un conjunto de funciones mutuamente recursivas.

Recurrencia anónima

La recursividad generalmente se realiza llamando explícitamente a una función por su nombre. Sin embargo, la recursividad también se puede realizar llamando implícitamente a una función basada en el contexto actual, lo que es particularmente útil para funciones anónimas y se conoce como recursividad anónima.

Recurrencia estructural versus generativa

Algunos autores clasifican la recursividad como "estructural" o "generativa". La distinción está relacionada con dónde obtiene un procedimiento recursivo los datos con los que trabaja y cómo procesa esos datos:

[Las funciones que consumen datos estructurados] normalmente descomponen sus argumentos en sus componentes estructurales inmediatos y luego procesan esos componentes. Si uno de los componentes inmediatos pertenece a la misma clase de datos que la entrada, la función es recursiva. Por esa razón, nos referimos a estas funciones como FUNCIONES (ESTRUCTURALMENTE) RECURSIVAS.

— Felleisen, Findler, Flatt y Krishnaurthi, Cómo diseñar programas , 2001

Por lo tanto, la característica definitoria de una función estructuralmente recursiva es que el argumento de cada llamada recursiva es el contenido de un campo de la entrada original. La recursividad estructural incluye casi todos los recorridos de árboles, incluido el procesamiento XML, la creación y búsqueda de árboles binarios, etc. Al considerar la estructura algebraica de los números naturales (es decir, un número natural es cero o el sucesor de un número natural), funciones como como factorial también puede considerarse como recursividad estructural.

La recursividad generativa es la alternativa:

Muchos algoritmos recursivos bien conocidos generan una pieza de datos completamente nueva a partir de los datos dados y recurren a ellos. HtDP ( Cómo diseñar programas ) se refiere a este tipo como recursividad generativa. Los ejemplos de recursividad generativa incluyen: gcd, clasificación rápida, búsqueda binaria, clasificación por fusión, método de Newton, fractales e integración adaptativa.

— Matthias Felleisen, Programación funcional avanzada , 2002

Esta distinción es importante para probar la terminación de una función.

Se puede demostrar fácilmente que todas las funciones estructuralmente recursivas en estructuras de datos finitas (definidas inductivamente) terminan, a través de la inducción estructural: intuitivamente, cada llamada recursiva recibe una porción más pequeña de datos de entrada, hasta que se alcanza un caso base.
Las funciones recursivas generativas, por el contrario, no alimentan necesariamente una entrada más pequeña a sus llamadas recursivas, por lo que la prueba de su terminación no es necesariamente tan simple, y evitar bucles infinitos requiere un mayor cuidado. Estas funciones generativamente recursivas a menudo se pueden interpretar como funciones correcursivas (cada paso genera los nuevos datos, como la aproximación sucesiva en el método de Newton) y terminar esta correcursión requiere que los datos finalmente satisfagan alguna condición, que no necesariamente está garantizada.
En términos de variantes de bucle, la recursividad estructural es cuando hay una variante de bucle obvia, a saber, el tamaño o la complejidad, que comienza siendo finito y disminuye en cada paso recursivo.
Por el contrario, la recursión generativa es cuando no existe una variante de bucle tan obvia y la terminación depende de una función, como "error de aproximación", que no necesariamente disminuye a cero y, por lo tanto, la terminación no está garantizada sin más análisis.

Problemas de implementación

En la implementación real, en lugar de una función recursiva pura (verificación única para el caso base, de lo contrario, paso recursivo), se pueden realizar una serie de modificaciones, con fines de claridad o eficiencia. Éstos incluyen:

Función de envoltorio (en la parte superior)
Cortocircuitando el caso base, también conocido como "recursión de plena competencia" (en la parte inferior)
Algoritmo híbrido (en la parte inferior): cambiar a un algoritmo diferente una vez que los datos son lo suficientemente pequeños

Sobre la base de la elegancia, las funciones de envoltorio generalmente se aprueban, mientras que cortocircuitar el caso base está mal visto, particularmente en la academia. Los algoritmos híbridos se utilizan a menudo por motivos de eficiencia, para reducir la sobrecarga de la recursividad en casos pequeños, y la recursividad en condiciones de plena competencia es un caso especial de esto.

Función de envoltorio

Una función contenedora es una función que se llama directamente pero que no recurre a sí misma, sino que llama a una función auxiliar separada que en realidad hace la recursión.

Las funciones contenedoras se pueden usar para validar parámetros (para que la función recursiva pueda omitirlos), realizar inicializaciones (asignar memoria, inicializar variables), particularmente para variables auxiliares como "nivel de recursión" o cálculos parciales para memorización, y manejar excepciones y errores. En los lenguajes que admiten funciones anidadas, la función auxiliar se puede anidar dentro de la función contenedora y usar un ámbito compartido. En ausencia de funciones anidadas, las funciones auxiliares son, en cambio, una función separada, si es posible privada (ya que no se las llama directamente), y la información se comparte con la función contenedora mediante el uso de pass-by-reference.

Cortocircuitando el caso base

recursividad ordinaria	recursividad de cortocircuito
int fac1 (int n) { si (norte <= 0) devolver 1; más volver fac1 (n -1) * n; }	int estático fac2 (int n) { // afirmar(n >= 2); si (norte == 2) devolver 2; más volver fac2 (n -1) * n; } int fac2wrapper (int n) { si (norte <= 1) devolver 1; más devolver fac2 (n); }

Cortocircuitar el caso base, también conocido como recursividad de plena competencia, consiste en verificar el caso base anteshacer una llamada recursiva, es decir, verificar si la próxima llamada será el caso base, en lugar de llamar y luego verificar el caso base. El cortocircuito se realiza particularmente por razones de eficiencia, para evitar la sobrecarga de una llamada de función que regresa inmediatamente. Tenga en cuenta que dado que el caso base ya se ha verificado (inmediatamente antes del paso recursivo), no es necesario verificarlo por separado, pero sí es necesario usar una función de contenedor para el caso cuando la recursividad general comienza con el caso base. sí mismo. Por ejemplo, en la función factorial, propiamente el caso base es 0! = 1, ¡mientras que devuelve inmediatamente 1 por 1! es un cortocircuito y puede perder 0; esto puede ser mitigado por una función contenedora. El cuadro muestra el código C para atajar los casos factoriales 0 y 1.

Los cortocircuitos son principalmente una preocupación cuando se encuentran muchos casos base, como punteros nulos en un árbol, que pueden ser lineales en el número de llamadas a funciones, por lo tanto, ahorros significativos para los algoritmos O (n); esto se ilustra a continuación para una búsqueda en profundidad. El cortocircuito en un árbol corresponde a considerar una hoja (nodo no vacío sin hijos) como caso base, en lugar de considerar un nodo vacío como caso base. Si solo hay un caso base único, como en el cálculo del factorial, el cortocircuito proporciona solo ahorros de O (1).

Conceptualmente, se puede considerar que el cortocircuito tiene el mismo caso base y el mismo paso recursivo, verificando el caso base solo antes de la recurrencia, o se puede considerar que tiene un caso base diferente (un paso eliminado del caso base estándar) y un paso recursivo más complejo, a saber, "comprobar válido y luego repetir", como al considerar los nodos de hoja en lugar de los nodos nulos como casos base en un árbol. Debido a que el cortocircuito tiene un flujo más complicado, en comparación con la clara separación del caso base y el paso recursivo en la recursividad estándar, a menudo se considera un estilo deficiente, particularmente en el mundo académico.

Búsqueda en profundidad

Un ejemplo básico de cortocircuito se da en la búsqueda en profundidad (DFS) de un árbol binario; vea la sección de árboles binarios para una discusión recursiva estándar.

El algoritmo recursivo estándar para un DFS es:

caso base: si el nodo actual es nulo, devuelve falso
paso recursivo: de lo contrario, verifique el valor del nodo actual, devuelva verdadero si coincide, de lo contrario recurse en los niños

En cortocircuito, esto es en cambio:

verifique el valor del nodo actual, devuelva verdadero si coincide,
de lo contrario, en niños, si no es Nulo, entonces recurse.

En términos de los pasos estándar, esto mueve la verificación del caso base antes del paso recursivo. Alternativamente, estos pueden considerarse una forma diferente de caso base y paso recursivo, respectivamente. Tenga en cuenta que esto requiere una función contenedora para manejar el caso cuando el árbol en sí está vacío (el nodo raíz es Nulo).

En el caso de un árbol binario perfecto de altura h, hay 2 −1 nodos y 2 punteros nulos como hijos (2 para cada una de las 2 hojas), por lo que el cortocircuito reduce el número de llamadas a la función a la mitad en el peor de los casos..

En C, el algoritmo recursivo estándar puede implementarse como:

bool tree_contains (struct node * tree_node, int i) {      
    si (árbol_nodo == NULL)   
        devolver falso; // caso base si no (tree_node -> datos == i)   
        
        devolver verdadero; 
    más
        devuelve tree_contains (tree_node -> izquierda, i) ||   
               tree_contains (tree_node -> derecha, i); 
}

El algoritmo cortocircuitado se puede implementar como:

// Función contenedora para manejar el árbol vacío 
bool tree_contains (struct node * tree_node, int i) {      
    si (árbol_nodo == NULL)   
        devolver falso; // árbol vacío más   
    
        return tree_contains_do (tree_node, i); // llamar a la función auxiliar }    


// Supone tree_node != NULL 
bool tree_contains_do (struct node * tree_node, int i) {      
    if (nodo_árbol -> datos == i)   
        devolver verdadero; // encontrado otra cosa // retorno recursivo (tree_node -> left && tree_contains_do (tree_node -> left, i)) ||   
      
               
               (tree_node -> right && tree_contains_do (tree_node -> right, i));   
}

Tenga en cuenta el uso de la evaluación de cortocircuito de los operadores booleanos && (AND), de modo que la llamada recursiva se realice solo si el nodo es válido (no nulo). Tenga en cuenta que mientras el primer término en AND es un puntero a un nodo, el segundo término es un booleano, por lo que la expresión general se evalúa como un booleano. Este es un idioma común en el cortocircuito recursivo. Esto se suma a la evaluación de cortocircuito del booleano || (OR), para verificar solo el hijo derecho si el hijo izquierdo falla. De hecho, todo el flujo de control de estas funciones se puede reemplazar con una sola expresión booleana en una declaración de retorno, pero la legibilidad no se ve afectada por la eficiencia.

Algoritmo híbrido

Los algoritmos recursivos a menudo son ineficientes para datos pequeños, debido a la sobrecarga de llamadas y devoluciones de funciones repetidas. Por esta razón, las implementaciones eficientes de algoritmos recursivos a menudo comienzan con el algoritmo recursivo, pero luego cambian a un algoritmo diferente cuando la entrada se vuelve pequeña. Un ejemplo importante es la ordenación por fusión, que a menudo se implementa cambiando a la ordenación por inserción no recursiva cuando los datos son lo suficientemente pequeños, como en la ordenación por fusión en mosaico. Los algoritmos recursivos híbridos a menudo se pueden refinar aún más, como en Timsort, derivados de una clasificación híbrida de fusión/clasificación por inserción.

Recursión versus iteración

Anidamiento de la recursión dentro de un ciclo recursivo

La recursividad y la iteración son igualmente expresivas: la recursividad se puede reemplazar por la iteración con una pila de llamadas explícita, mientras que la iteración se puede reemplazar por la recursividad final. El enfoque preferible depende del problema que se esté considerando y del lenguaje utilizado. En la programación imperativa, se prefiere la iteración, particularmente para la recursividad simple, ya que evita la sobrecarga de las llamadas a funciones y la gestión de la pila de llamadas, pero la recursividad generalmente se usa para recursividad múltiple. Por el contrario, en los lenguajes funcionales se prefiere la recursividad, y la optimización de recursividad de cola genera poca sobrecarga. La implementación de un algoritmo mediante iteración puede no ser fácil de lograr.

Compare las plantillas para calcular x _n definido por x _n = f(n, x _n-1) a partir de x _base:

función recursiva(n) si n == base retorno x _base más devuelve f(n, recursiva(n-1))

función iterativa(n) x = _{base x} para i = base+1 a n x = f(yo, x) volver x

Para un lenguaje imperativo, la sobrecarga es para definir la función, y para un lenguaje funcional, la sobrecarga es para definir la variable acumuladora x.

Por ejemplo, una función factorial puede implementarse iterativamente en C asignando una variable de índice de bucle y una variable de acumulador, en lugar de pasar argumentos y devolver valores por recursión:

int sin signo factorial (int sin signo n) {     
  producto int sin signo = 1; // el producto vacio es 1 while (n) {     
    
    producto *= n;  
    -- n;
  }
  devolución del producto; 
}

Poder expresivo

La mayoría de los lenguajes de programación en uso hoy en día permiten la especificación directa de funciones y procedimientos recursivos. Cuando se llama a una función de este tipo, el entorno de tiempo de ejecución del programa realiza un seguimiento de las diversas instancias de la función (a menudo mediante una pila de llamadas, aunque se pueden utilizar otros métodos). Cada función recursiva se puede transformar en una función iterativa reemplazando las llamadas recursivas con construcciones de control iterativo y simulando la pila de llamadas con una pila administrada explícitamente por el programa.

Por el contrario, todas las funciones y procedimientos iterativos que pueden ser evaluados por una computadora (ver Completitud de Turing) pueden expresarse en términos de funciones recursivas; Las construcciones de control iterativo, como los bucles while y for, se reescriben de forma rutinaria en forma recursiva en lenguajes funcionales.Sin embargo, en la práctica, esta reescritura depende de la eliminación de llamadas de cola, que no es una característica de todos los idiomas. C, Java y Python son lenguajes principales notables en los que todas las llamadas a funciones, incluidas las llamadas finales, pueden causar una asignación de pila que no ocurriría con el uso de construcciones en bucle; en estos lenguajes, un programa iterativo en funcionamiento reescrito en forma recursiva puede desbordar la pila de llamadas, aunque la eliminación de llamadas finales puede ser una característica que no está cubierta por la especificación de un lenguaje, y diferentes implementaciones del mismo lenguaje pueden diferir en las capacidades de eliminación de llamadas finales.

Problemas de desempeño

En los lenguajes (como C y Java) que favorecen las construcciones de bucles iterativos, generalmente hay un costo significativo de tiempo y espacio asociado con los programas recursivos, debido a la sobrecarga requerida para administrar la pila y la relativa lentitud de las llamadas a funciones; en los lenguajes funcionales, una llamada de función (particularmente una llamada de cola) suele ser una operación muy rápida y la diferencia suele ser menos notable.

Como ejemplo concreto, la diferencia de rendimiento entre las implementaciones iterativas y recursivas del ejemplo "factorial" anterior depende en gran medida del compilador utilizado. En los lenguajes donde se prefieren las construcciones de bucle, la versión iterativa puede ser hasta varios órdenes de magnitud más rápida que la recursiva. En lenguajes funcionales, la diferencia de tiempo total de las dos implementaciones puede ser insignificante; de hecho, el costo de multiplicar primero los números más grandes en lugar de los números más pequeños (lo que ocurre con la versión iterativa que se da aquí) puede abrumar el tiempo ahorrado al elegir la iteración.

Espacio de pila

En algunos lenguajes de programación, el tamaño máximo de la pila de llamadas es mucho menor que el espacio disponible en el montón y los algoritmos recursivos tienden a requerir más espacio de pila que los algoritmos iterativos. En consecuencia, estos lenguajes a veces imponen un límite en la profundidad de la recursividad para evitar desbordamientos de pila; Python es uno de esos lenguajes. Tenga en cuenta la advertencia a continuación con respecto al caso especial de recursión de cola.

Vulnerabilidad

Debido a que los algoritmos recursivos pueden estar sujetos a desbordamientos de pila, pueden ser vulnerables a entradas patológicas o maliciosas. Algunos programas maliciosos se dirigen específicamente a la pila de llamadas de un programa y aprovechan la naturaleza inherentemente recursiva de la pila. Incluso en ausencia de malware, un desbordamiento de pila causado por una recurrencia ilimitada puede ser fatal para el programa, y la lógica de manejo de excepciones puede no evitar que el proceso correspondiente finalice.

Multiplicar problemas recursivos

Los problemas recursivos de multiplicación son inherentemente recursivos, debido al estado previo que necesitan rastrear. Un ejemplo es el cruce de árboles como en la búsqueda primero en profundidad; aunque se utilizan métodos recursivos e iterativos, contrastan con el recorrido de listas y la búsqueda lineal en una lista, que es un método únicamente recursivo y, por lo tanto, naturalmente iterativo. Otros ejemplos incluyen algoritmos de divide y vencerás como Quicksort y funciones como la función de Ackermann. Todos estos algoritmos se pueden implementar de forma iterativa con la ayuda de una pila explícita, pero el esfuerzo del programador involucrado en la gestión de la pila y la complejidad del programa resultante posiblemente superen cualquier ventaja de la solución iterativa.

Refactorización de recursividad

Los algoritmos recursivos se pueden reemplazar con contrapartes no recursivas. Un método para reemplazar algoritmos recursivos es simularlos usando memoria de montón en lugar de memoria de pila. Una alternativa es desarrollar un algoritmo de reemplazo completamente basado en métodos no recursivos, lo que puede ser un desafío. Por ejemplo, los algoritmos recursivos para emparejar comodines, como el algoritmo wildmat de Rich Salz, alguna vez fueron típicos. Se han desarrollado algoritmos no recursivos para el mismo propósito, como el algoritmo de comodines de coincidencia de Krauss, para evitar los inconvenientes de la recursividad y se han mejorado solo gradualmente en función de técnicas como la recopilación de pruebas y el rendimiento de perfiles.

Funciones recursivas de cola

Las funciones recursivas de cola son funciones en las que todas las llamadas recursivas son llamadas de cola y, por lo tanto, no acumulan ninguna operación diferida. Por ejemplo, la función gcd (que se muestra nuevamente a continuación) es recursiva en la cola. Por el contrario, la función factorial (también a continuación) no es recursiva en la cola; debido a que su llamada recursiva no está en la posición final, acumula operaciones de multiplicación diferidas que deben realizarse después de que se completa la llamada recursiva final. Con un compilador o intérprete que trata las llamadas recursivas de cola como saltos en lugar de llamadas a funciones, una función recursiva de cola como gcd se ejecutará usando un espacio constante. Por lo tanto, el programa es esencialmente iterativo, equivalente al uso de estructuras de control de lenguaje imperativas como los bucles "for" y "while".

Recurrencia de cola:	Aumento de la recursividad:
//ENTRADA: Enteros x, y tales que x >= y y y >= 0 int gcd (int x, int y) { si (y == 0) devuelve x; más devuelve mcd (y, x % y); }	//ENTRADA: n es un entero tal que n >= 0 int fact (int n) { si (norte == 0) devolver 1; más devuelve n * hecho (n - 1); }

La importancia de la recursión de cola es que cuando se realiza una llamada recursiva de cola (o cualquier llamada de cola), no es necesario guardar la posición de retorno de la persona que llama en la pila de llamadas; cuando la llamada recursiva regrese, se bifurcará directamente en la posición de retorno previamente guardada. Por lo tanto, en los lenguajes que reconocen esta propiedad de las llamadas de cola, la recursión de cola ahorra espacio y tiempo.

Orden de ejecución

Considere estas dos funciones:

Función 1

void función recursiva (int num) {   
    printf ("%d n ", numero); 
    si (num < 4)   
        función recursiva (num + 1);  
}

Función 2

void función recursiva (int num) {   
    si (num < 4)   
        función recursiva (num + 1);  
    printf ("%d n ", numero); 
}

La función 2 es la función 1 con las líneas intercambiadas.

En el caso de una función que se llama a sí misma una sola vez, las instrucciones colocadas antes de la llamada recursiva se ejecutan una vez por recursión antes que cualquiera de las instrucciones colocadas después de la llamada recursiva. Estos últimos se ejecutan repetidamente una vez alcanzada la recursividad máxima.

También tenga en cuenta que el orden de las declaraciones de impresión se invierte, lo que se debe a la forma en que las funciones y las declaraciones se almacenan en la pila de llamadas.

Procedimientos recursivos

Factorial

Un ejemplo clásico de un procedimiento recursivo es la función utilizada para calcular el factorial de un número natural: $operatorname {hecho} (n)={begin{casos}1&{mbox{si}}n=0\ncdot operatorname {hecho} (n-1)&{mbox{si}}n >0\end{casos}}$

Pseudocódigo (recursivo):
la función factorial es:entrada: entero n tal que n >= 0salida: [ n × (n -1) × (n -2) ×... × 1]1. si n es 0, devuelve 1 2. de lo contrario, devuelve [ n × factorial(n -1) ]end factorial

La función también se puede escribir como una relación de recurrencia: $b_{n}=nb_{n-1}$ $b_{0}=1$

Esta evaluación de la relación de recurrencia demuestra el cálculo que se realizaría al evaluar el pseudocódigo anterior:

Calculando la relación de recurrencia para n = 4:
segundo ₄ = 4 × segundo ₃ = 4 × (3 × _{segundo 2}) = 4 × (3 × (2 × b ₁)) = 4 × (3 × (2 × (1 × b ₀))) = 4 × (3 × (2 × (1 × 1))) = 4 × (3 × (2 × 1)) = 4 × (3 × 2) = 4 × 6 = 24

Esta función factorial también se puede describir sin usar la recursividad haciendo uso de las típicas construcciones de bucle que se encuentran en los lenguajes de programación imperativos:

Pseudocódigo (iterativo):
la función factorial es:entrada: entero n tal que n >= 0salida: [ n × (n -1) × (n -2) ×... × 1]1. crear una nueva variable llamada total_ejecutable con un valor de 12 bucle de inicio 1. si n es 0, salir del ciclo 2. establecer total_ejecutable en (total_ejecutable × n) 3. decrementar n 4. repetir bucle3. devolver total_ejecutableterminar factorial

Pseudocódigo (iterativo):

la función factorial es:entrada: entero n tal que n >= 0salida: [ n × (n -1) × (n -2) ×... × 1]1. crear una nueva variable llamada total_ejecutable con un valor de 12 bucle de inicio 1. si n es 0, salir del ciclo 2. establecer total_ejecutable en (total_ejecutable × n) 3. decrementar n 4. repetir bucle3. devolver total_ejecutableterminar factorial

El código imperativo anterior es equivalente a esta definición matemática usando una variable acumuladora t: ${displaystyle {begin{alineado}operatorname {hecho} (n)&=operatorname {hecho_{acc}} (n,1)\operatorname {hecho_{acc}} (n,t)&={ begin{cases}t&{mbox{if }}n=0\operatorname {fact_{acc}} (n-1,nt)&{mbox{if }}n>0\end{cases }}end{alineado}}}$

La definición anterior se traduce directamente a lenguajes de programación funcionales como Scheme; este es un ejemplo de iteración implementada recursivamente.

Máximo común divisor

El algoritmo de Euclides, que calcula el máximo común divisor de dos números enteros, se puede escribir de forma recursiva.

Definición de función: $gcd(x,y)={begin{casos}x&{mbox{if }}y=0\gcd(y,operatorname {resto} (x,y))&{mbox{if } }y>0\end{casos}}$

Pseudocódigo (recursivo):
la función gcd es: entrada: entero x, entero y tal que x > 0 e y >= 01. si y es 0, devuelve x 2. de lo contrario, devuelve [ gcd(y, (resto de x / y)) ]end mcd

Relación de recurrencia del máximo común divisor, donde $x%y$ expresa el resto de $x/y$ : $gcd(x,y)=gcd(y,x%y)$ si $yneq 0$ $mcd(x,0)=x$

Calculando la relación de recurrencia para x = 27 y y = 9:
mcd(27, 9) = mcd(9, 27 % 9) = mcd(9, 0) = 9
Calculando la relación de recurrencia para x = 111 y y = 259:
mcd(111, 259) = mcd(259, 111 % 259) = mcd(259, 111) = mcd(111, 259 % 111) = mcd(111, 37) = mcd(37, 111 % 37) = mcd(37, 0) = 37

El programa recursivo anterior es recursivo a la cola; es equivalente a un algoritmo iterativo, y el cálculo que se muestra arriba muestra los pasos de evaluación que realizaría un lenguaje que elimina las llamadas de cola. A continuación se muestra una versión del mismo algoritmo que usa iteración explícita, adecuada para un lenguaje que no elimina las llamadas de cola. Al mantener su estado completamente en las variables x e y y al usar una construcción de bucle, el programa evita realizar llamadas recursivas y hacer crecer la pila de llamadas.

Pseudocódigo (iterativo):
la función gcd es:entrada: entero x, entero y tal que x >= y y y >= 01. crea una nueva variable llamada resto2. comienza el ciclo 1. si y es cero, salir del ciclo 2. establecer el resto en el resto de x/y 3. establece x en y 4. establecer y en el resto 5. repetir bucle3. devolver xend gcd

El algoritmo iterativo requiere una variable temporal, e incluso conociendo el algoritmo de Euclides es más difícil entender el proceso por simple inspección, aunque los dos algoritmos son muy similares en sus pasos.

Torres de Hanoi

Las Torres de Hanoi es un rompecabezas matemático cuya solución ilustra la recursividad. Hay tres clavijas que pueden sostener pilas de discos de diferentes diámetros. Nunca se puede apilar un disco más grande encima de uno más pequeño. Comenzando con n discos en una clavija, deben moverse a otra clavija de uno en uno. ¿Cuál es el menor número de pasos para mover la pila?

Definición de función: $operatorname {hanoi} (n)={begin{casos}1&{mbox{if }}n=1\2cdot operatorname {hanoi} (n-1)+1&{mbox{if }} n>1\end{casos}}$

Relación de recurrencia para Hanoi: $h_{n}=2h_{n-1}+1$ $h_{1}=1$

Calculando la relación de recurrencia para n = 4:
hanoi(4) = 2×hanoi(3) + 1 = 2×(2×hanoi(2) + 1) + 1 = 2×(2×(2×hanoi(1) + 1) + 1) + 1 = 2×(2×(2×1 + 1) + 1) + 1 = 2×(2×(3) + 1) + 1 = 2×(7) + 1 = 15

Implementaciones de ejemplo:

Pseudocódigo (recursivo):
la función hanoi es:entrada: entero n, tal que n >= 11. si n es 1 , devuelve 12. devuelve [2 * [ call hanoi(n-1)] + 1]end hanoi

Aunque no todas las funciones recursivas tienen una solución explícita, la sucesión de la Torre de Hanoi se puede reducir a una fórmula explícita.

Una fórmula explícita para Towers of Hanoi:
h ₁ = 1 = 2 - 1 h ₂ = 3 = 2 - 1 h ₃ = 7 = 2 - 1 h ₄ = 15 = 2 - 1 h ₅ = 31 = 2 - 1 h ₆ = 63 = 2 - 1 h ₇ = 127 = 2 - 1 En general: h _n = 2 - 1, para todo n >= 1

Búsqueda binaria

El algoritmo de búsqueda binaria es un método para buscar un solo elemento en una matriz ordenada cortando la matriz por la mitad con cada pasada recursiva. El truco consiste en elegir un punto medio cerca del centro de la matriz, comparar los datos en ese punto con los datos que se buscan y luego responder a una de las tres condiciones posibles: los datos se encuentran en el punto medio, los datos en el punto medio son mayores que los datos que se buscan, o los datos en el punto medio son menores que los datos que se buscan.

La recursividad se usa en este algoritmo porque con cada pasada se crea una nueva matriz cortando la anterior por la mitad. El procedimiento de búsqueda binaria se llama recursivamente, esta vez en la matriz nueva (y más pequeña). Normalmente, el tamaño de la matriz se ajusta manipulando un índice inicial y final. El algoritmo exhibe un orden logarítmico de crecimiento porque esencialmente divide el dominio del problema por la mitad con cada paso.

Ejemplo de implementación de búsqueda binaria en C:

 /* 
  Llame a binary_search con las condiciones iniciales adecuadas.

  ENTRADA: 
    los datos son una matriz de enteros ORDENADOS en orden ASCENDENTE, 
    toFind es el entero a buscar, 
    count es el número total de elementos en la matriz

  SALIDA: 
    resultado de binary_search

*/
 búsqueda int (int * data, int toFind, int count)      
 {
    // Inicio = 0 (índice inicial) 
// Fin = recuento - 1 (índice superior) return binary_search (datos, toFind, 0, recuento -1);    
        
 }

 /* 
   Algoritmo de búsqueda binaria.

   ENTRADA: 
        los datos son una matriz de enteros ORDENADOS en orden ASCENDENTE, 
        toFind es el entero a buscar, 
        start es el índice mínimo de la matriz, 
        end es el índice máximo de la matriz 
   SALIDA: 
        posición del entero a buscar dentro de los datos de la matriz, 
        -1 si no se encuentra 
*/
 int binary_search (int * data, int toFind, int start, int end)        
 {
    //Obtener el punto medio. 
int mid = inicio + (fin - inicio) / 2; //División entera              


    if (inicio > fin) //Condición de parada (caso base) return -1;                        
        
    else if (data [ mid ] == toFind) //Encontrado, retorno de índice return mid;            
        
    else if (data [ mid ] > toFind) //Los datos son mayores que toFind, busca la mitad inferior return binary_search (data, toFind, start, mid -1);             
           
    else // Los datos son menores que toFind, buscar en la mitad superior return binary_search (data, toFind, mid + 1, end);                                 
           
 }

Estructuras de datos recursivas (recursión estructural)

Una aplicación importante de la recursividad en informática es la definición de estructuras de datos dinámicas, como listas y árboles. Las estructuras de datos recursivas pueden crecer dinámicamente hasta un tamaño teóricamente infinito en respuesta a los requisitos de tiempo de ejecución; por el contrario, el tamaño de una matriz estática debe establecerse en tiempo de compilación.

"Los algoritmos recursivos son particularmente apropiados cuando el problema subyacente o los datos a tratar se definen en términos recursivos".

Los ejemplos de esta sección ilustran lo que se conoce como "recursión estructural". Este término se refiere al hecho de que los procedimientos recursivos actúan sobre datos que se definen recursivamente.

Siempre que un programador derive la plantilla de una definición de datos, las funciones emplean recursividad estructural. Es decir, las recursiones en el cuerpo de una función consumen una parte inmediata de un valor compuesto dado.

Listas enlazadas

A continuación se muestra una definición en C de una estructura de nodo de lista enlazada. Observe especialmente cómo se define el nodo en términos de sí mismo. El elemento "siguiente" del nodo de estructura es un puntero a otro nodo de estructura, creando efectivamente un tipo de lista.

 nodo de estructura
{
  datos int; // algunos datos enteros struct node * next; // puntero a otro nodo de estructura };

Debido a que la estructura de datos del nodo struct se define de forma recursiva, los procedimientos que operan en ella se pueden implementar de forma natural como procedimientos recursivos. El procedimiento list_print definido a continuación recorre la lista hasta que está vacía (es decir, el puntero de la lista tiene un valor NULL). Para cada nodo, imprime el elemento de datos (un número entero). En la implementación de C, la lista permanece sin cambios por el procedimiento list_print.

void list_print (estructura nodo * lista)   
{
    if (lista != NULL) // caso base {                  
    
       printf ("%d", lista -> datos); // imprime datos enteros seguidos de un espacio list_print (lista -> siguiente); // llamada recursiva en el siguiente nodo }    
             
    
}

árboles binarios

A continuación se muestra una definición simple para un nodo de árbol binario. Al igual que el nodo de las listas enlazadas, se define recursivamente en términos de sí mismo. Hay dos punteros autorreferenciales: izquierdo (que apunta al subárbol izquierdo) y derecho (que apunta al subárbol derecho).

 nodo de estructura
{
  datos int; // alguna estructura de datos enteros nodo * izquierda; // puntero al subárbol izquierdo struct node * right; // apunta al subárbol derecho };

Las operaciones en el árbol se pueden implementar usando recursividad. Tenga en cuenta que debido a que hay dos punteros autorreferenciales (izquierdo y derecho), las operaciones de árbol pueden requerir dos llamadas recursivas:

// Prueba si tree_node contiene i; devuelva 1 si es así, 0 si no. 
int tree_contains (struct node * tree_node, int i) {      
    si (árbol_nodo == NULL)   
        devolver 0; // caso base si no (tree_node -> datos == i)   
        
        devolver 1; 
    más
        devuelve tree_contains (tree_node -> izquierda, i) || tree_contains (tree_node -> derecha, i);     
}

Se realizarán como máximo dos llamadas recursivas para cualquier llamada dada a tree_contains como se definió anteriormente.

// Recorrido en orden: 
void tree_print (struct node * tree_node) {    
    if (tree_node != NULL) { // caso base tree_print (tree_node -> izquierda); // ir a la izquierda printf ("%d", tree_node -> data); // imprime el entero seguido de un espacio tree_print (tree_node -> right); // ir a la derecha }                  
              
            
             
    
}

El ejemplo anterior ilustra un recorrido en orden del árbol binario. Un árbol de búsqueda binario es un caso especial del árbol binario donde los elementos de datos de cada nodo están en orden.

Travesía del sistema de archivos

Dado que la cantidad de archivos en un sistema de archivos puede variar, la recursividad es la única forma práctica de atravesar y, por lo tanto, enumerar su contenido. Atravesar un sistema de archivos es muy similar a atravesar un árbol, por lo tanto, los conceptos detrás del recorrido de un árbol son aplicables a atravesar un sistema de archivos. Más específicamente, el siguiente código sería un ejemplo de un recorrido de preorden de un sistema de archivos.

importar  java.io.File ;

 sistema de archivos de clase  pública { 

	public  static  void  main (String  []  args)  {
		atravesar ();
	}

	/**
	 * Obtiene las raíces del sistema de archivos
	 * Continúa con el recorrido del sistema de archivos recursivo
	 */
	 recorrido de vacío estático  privado () {  
		Archivo []  fs  =  Archivo. listRoots ();
		for  (int  i  =  0;  i  <  fs. longitud;  i ++)  {
			sistema _ fuera _ println (fs [ i ]);
			if  (fs [ i ]. isDirectory ()  &&  fs [ i ]. canRead ())  {
				rtraversa (fs [ i ]);
			}
		}
	}

	/**
	 * Atraviesa recursivamente un directorio dado
	 *
	 * @param fd indica el punto de partida del recorrido
	 */
	privado  estático  vacío  rtraverse (Archivo  fd)  {
		Archivo []  fss  =  fd. listararchivos ();

		para  (int  i  =  0;  i  <  fss. longitud;  i ++)  {
			sistema _ fuera _ println (fss [ i ]);
			if  (fss [ i ]. isDirectory ()  &&  fss [ i ]. canRead ())  {
				rtraversa (fss [ i ]);
			}
		}
	}

}

Este código es a la vez recursivo e iterativo: los archivos y directorios se iteran y cada directorio se abre de forma recursiva.

El método "rtraverse" es un ejemplo de recursividad directa, mientras que el método "traverse" es una función contenedora.

El escenario del "caso base" es que siempre habrá un número fijo de archivos y/o directorios en un sistema de archivos determinado.

Tiempo-eficiencia de algoritmos recursivos

La eficiencia temporal de los algoritmos recursivos se puede expresar en una relación de recurrencia de notación Big O. Pueden (generalmente) luego simplificarse en un solo término Big-O.

Regla de atajo (teorema maestro)

Si la complejidad temporal de la función está en la forma

Entonces el Gran O de la complejidad temporal es así:

Si ${displaystyle f(n)=O(n^{log _{b}a-varepsilon})}$ para alguna constante $varepsilon >0$ , entonces ${displaystyle T(n)=Theta (n^{log _{b}a})}$
si ${displaystyle f(n)=Theta (n^{log _{b}a})}$ , entonces ${displaystyle T(n)=Theta (n^{log _{b}a}log n)}$
Si ${displaystyle f(n)=Omega (n^{log _{b}a+varepsilon})}$ para alguna constante $varepsilon >0$ , y si ${displaystyle acdot f(n/b)leq ccdot f(n)}$ para alguna constante c < 1 y todas n suficientemente grandes, entonces ${displaystyle T(n)=Theta (f(n))}$

donde a representa el número de llamadas recursivas en cada nivel de recursividad, b representa por qué factor menor es la entrada para el siguiente nivel de recursión (es decir, el número de partes en las que divide el problema), y f (n) representa el trabajo que la función hace independientemente de cualquier recursión (por ejemplo, partición, recombinación) en cada nivel de recursión.

Contenido relacionado

Más resultados...