Razonamiento logico
| ||||||||||||||||||||||||||||||||||||||||||||||||
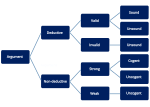
| El razonamiento lógico se refiere a la corrección de los argumentos. Una distinción clave es entre argumentos deductivos y no deductivos. |
razonamiento lógico es una actividad mental que tiene como objetivo llegar a una conclusión de forma rigurosa. Ocurre en forma de inferencias o argumentos partiendo de un conjunto de premisas y razonamiento hasta una conclusión respaldada por estas premisas. Las premisas y la conclusión son proposiciones, es decir, afirmaciones verdaderas o falsas sobre el caso. Juntos, forman un argumento. El razonamiento lógico está regido por normas en el sentido de que apunta a formular argumentos correctos que cualquier persona racional encontraría convincentes. La principal disciplina que estudia el razonamiento lógico se llama lógica.
Los distintos tipos de razonamiento lógico difieren entre sí en cuanto a las normas que emplean y la certeza de la conclusión a la que llegan. El razonamiento deductivo ofrece el apoyo más fuerte: las premisas aseguran la conclusión, lo que significa que es imposible que la conclusión sea falsa si todas las premisas son verdaderas. Tal argumento se llama argumento válido, por ejemplo: todos los hombres son mortales; Sócrates es un hombre; por tanto, Sócrates es mortal. Para argumentos válidos, no es importante si las premisas son realmente verdaderas, sino sólo que, si fueran verdaderas, la conclusión no podría ser falsa. Los argumentos válidos siguen una regla de inferencia, como modus ponens o modus tollens. El razonamiento deductivo juega un papel central en la lógica formal y las matemáticas.
Para el razonamiento lógico no deductivo, las premisas hacen que su conclusión sea racionalmente convincente sin garantizar su verdad. Esto suele entenderse en términos de probabilidad: las premisas hacen que sea más probable que la conclusión sea verdadera y las inferencias sólidas la hacen muy probable. Queda cierta incertidumbre porque la conclusión introduce nueva información que aún no se encuentra en las premisas. El razonamiento no deductivo juega un papel central en la vida cotidiana y en la mayoría de las ciencias. Los tipos que se analizan a menudo son el razonamiento inductivo, abductivo y analógico. El razonamiento inductivo es una forma de generalización que infiere una ley universal a partir de un patrón que se encuentra en muchos casos individuales. Se puede utilizar para concluir que "todos los cuervos son negros" Basado en muchas observaciones individuales de cuervos negros. El razonamiento abductivo, también conocido como "inferencia hacia la mejor explicación", comienza a partir de una observación y razona el hecho que explica esta observación. Un ejemplo es un médico que examina los síntomas de su paciente para hacer un diagnóstico de la causa subyacente. El razonamiento analógico compara dos sistemas similares. Observa que uno de ellos tiene una característica y concluye que el otro también la tiene.
Los argumentos que no cumplen con los estándares del razonamiento lógico se denominan falacias. Para las falacias formales, como afirmar el consecuente, el error reside en la forma lógica del argumento. Para las falacias informales, como los falsos dilemas, la fuente del razonamiento defectuoso suele encontrarse en el contenido o el contexto del argumento. Algunos teóricos entienden el razonamiento lógico en un sentido amplio que equivale aproximadamente al pensamiento crítico. En este sentido, abarca habilidades cognitivas además de la capacidad de sacar conclusiones a partir de premisas. Algunos ejemplos son las habilidades para generar y evaluar razones y evaluar la confiabilidad de la información. Otros factores son buscar nueva información, evitar inconsistencias y considerar las ventajas y desventajas de diferentes cursos de acción antes de tomar una decisión.
Definición
El razonamiento lógico es una forma de pensamiento que se ocupa de llegar a una conclusión de manera rigurosa. Esto sucede en forma de inferencias transformando la información presente en un conjunto de premisas para llegar a una conclusión. Puede definirse como "seleccionar e interpretar información de un contexto determinado, establecer conexiones y verificar y sacar conclusiones basadas en la información proporcionada e interpretada y las reglas y procesos asociados". El razonamiento lógico es riguroso en el sentido de que no genera ninguna conclusión pero asegura que las premisas respalden la conclusión y actúen como razones para creerla. Un aspecto central es que este apoyo no se limita a un razonador específico sino que cualquier persona racional encontraría convincente la conclusión basada en las premisas. De esta manera, el razonamiento lógico juega un papel en la ampliación del conocimiento.
La principal disciplina que estudia el razonamiento lógico se llama lógica. Se divide en lógica formal e informal, que estudian el razonamiento lógico formal e informal. Tradicionalmente, el razonamiento lógico se asociaba principalmente con el razonamiento deductivo estudiado por la lógica formal. Pero en un sentido más amplio, también incluye formas de razonamiento no deductivo, como el razonamiento inductivo, abductivo y analógico.
Las formas de razonamiento lógico tienen en común que utilizan premisas para hacer inferencias de una manera gobernada por normas. Como prácticas gobernadas por normas, apuntan a un acuerdo intersubjetivo sobre la aplicación de las normas, es decir, un acuerdo sobre si las premisas apoyan su conclusión y en qué medida. Los tipos de razonamiento lógico difieren en cuanto a las normas exactas que utilizan, así como en la certeza de la conclusión a la que llegan. El razonamiento deductivo ofrece el apoyo más fuerte e implica su conclusión con certeza, como las pruebas matemáticas. Para el razonamiento no deductivo, las premisas hacen que la conclusión sea más probable pero no la aseguran. Este apoyo se da en grados: argumentos sólidos hacen que la conclusión sea muy probable, como ocurre con cuestiones bien investigadas en las ciencias empíricas. Algunos teóricos dan una definición muy amplia de razonamiento lógico que incluye su papel como habilidad cognitiva responsable del pensamiento de alta calidad. En este sentido, tiene aproximadamente el mismo significado que el pensamiento crítico.
Conceptos básicos
En el estudio y análisis del razonamiento lógico se utiliza una variedad de conceptos básicos. El razonamiento lógico se produce al inferir una conclusión a partir de un conjunto de premisas. Las premisas y las conclusiones normalmente se consideran proposiciones. Una proposición es una afirmación que hace una afirmación sobre cuál es el caso. En este sentido, las proposiciones actúan como portadoras de verdad: son verdaderas o falsas. Por ejemplo, la frase "El agua está hirviendo". expresa una proposición ya que puede ser verdadera o falsa. Las frases "¿Está hirviendo el agua?" o "¡Hervir el agua!", por otro lado, no expresan proposiciones ya que no son ni verdaderas ni falsas. Las proposiciones utilizadas como punto de partida del razonamiento lógico se denominan premisas. La proposición que se infiere de ellos se llama conclusión. Por ejemplo, en el argumento “todos los cachorros son perros; todos los perros son animales; por lo tanto todos los cachorros son animales", las proposiciones "todos los cachorros son perros" y "todos los perros son animales" actúan como premisas mientras que la proposición "todos los cachorros son animales" es la conclusión.
Un conjunto de premisas junto con una conclusión se llama argumento. Una inferencia es el proceso mental de razonamiento que parte de las premisas y llega a la conclusión. Pero los términos "argumento" y "inferencia" A menudo se usan indistintamente en lógica. El propósito de los argumentos es convencer a una persona de que algo es así, proporcionando razones para esta creencia. Muchos argumentos en lenguaje natural no establecen explícitamente todas las premisas. En cambio, las premisas a menudo se asumen implícitamente, especialmente si parecen obvias y pertenecen al sentido común. Algunos teóricos distinguen entre argumentos simples y complejos. Un argumento complejo se compone de muchos subargumentos. De esta manera, se forma una cadena en la que las conclusiones de argumentos anteriores actúan como premisas para argumentos posteriores. Cada eslabón de esta cadena tiene que tener éxito para que un argumento complejo tenga éxito.
Un argumento es correcto o incorrecto dependiendo de si las premisas ofrecen apoyo a la conclusión. Esto a menudo se entiende en términos de probabilidad: si las premisas de un argumento correcto son verdaderas, aumenta la probabilidad de que su conclusión también lo sea. Se pueden distinguir formas de razonamiento lógico en función de cómo las premisas respaldan la conclusión. Los argumentos deductivos ofrecen el apoyo más sólido posible. Los argumentos no deductivos son más débiles pero, no obstante, son formas correctas de razonamiento. El término "prueba" Se utiliza a menudo para argumentos deductivos o argumentos no deductivos muy sólidos. Los argumentos incorrectos no ofrecen apoyo suficiente o no lo son y se denominan falacias, aunque el uso de argumentos incorrectos no significa que sus conclusiones sean incorrectas.
Razonamiento deductivo
El razonamiento deductivo es el proceso mental de sacar inferencias deductivas. Las inferencias deductivamente válidas son la forma más fiable de inferencia: es imposible que su conclusión sea falsa si todas las premisas son verdaderas. Esto significa que la verdad de las premisas asegura la verdad de la conclusión. Un argumento deductivo es sólido si es válido y todas sus premisas son verdaderas. Por ejemplo, inferir la conclusión "ningún gato es rana" del local "todas las ranas son anfibios" y "ningún gato es anfibio" es un argumento sólido. Pero incluso los argumentos con premisas falsas pueden ser deductivamente válidos, como inferir que "ningún gato es rana"; desde el local "todas las ranas son mamíferos" y "ningún gato es mamífero". En este sentido, sólo importa que la conclusión no pueda ser falsa si las premisas son verdaderas y no si realmente lo son.
Los argumentos deductivamente válidos siguen una regla de inferencia. Una regla de inferencia es un esquema para sacar conclusiones que depende sólo de la forma lógica de las premisas y la conclusión, pero no de su contenido específico. La regla de inferencia más discutida es el modus ponens. Tiene la siguiente forma: p; si p entonces q; por lo tanto q. Este esquema es deductivamente válido sin importar lo que representen p y q. Por ejemplo, el argumento “hoy es domingo; si hoy es domingo entonces no tengo que ir a trabajar hoy; por lo tanto no tengo que ir a trabajar hoy" es deductivamente válido porque tiene la forma de modus ponens. Otras reglas populares de inferencia incluyen modus tollens (no q; si p entonces q; por lo tanto, no p) y el silogismo disyuntivo (p o q; no p; por lo tanto, q).
Las reglas que gobiernan el razonamiento deductivo a menudo se expresan formalmente como sistemas lógicos para evaluar la exactitud de los argumentos deductivos. La lógica aristotélica es uno de los primeros sistemas y fue tratada como canon de la lógica en el mundo occidental durante más de dos mil años. Se basa en silogismos, como concluir que “Sócrates es un mortal”; de las premisas "Sócrates es un hombre" y "todos los hombres son mortales". El sistema actualmente dominante se conoce como lógica clásica y cubre muchas formas adicionales de inferencias además de los silogismos. Las llamadas lógicas extendidas se basan en la lógica clásica e introducen reglas de inferencia adicionales para dominios específicos. Por ejemplo, la lógica modal se puede utilizar para razonar sobre lo que es posible y lo que es necesario. La lógica temporal se puede utilizar para hacer inferencias sobre lo que sucedió antes, durante y después de un evento. La lógica clásica y sus extensiones se basan en un conjunto de intuiciones lógicas básicas aceptadas por la mayoría de los lógicos. Incluyen la ley del tercero excluido, la eliminación de la doble negación, el principio de explosión y la bivalencia de la verdad. Las llamadas lógicas desviadas rechazan algunas de estas intuiciones básicas y proponen reglas alternativas que rigen la validez de los argumentos. Por ejemplo, las lógicas intuicionistas rechazan la ley del tercero excluido y la eliminación de la doble negación, mientras que las lógicas paraconsistentes rechazan el principio de explosión.
El razonamiento deductivo juega un papel central en la lógica formal y las matemáticas. En matemáticas, se utiliza para demostrar teoremas matemáticos basados en un conjunto de premisas, normalmente llamadas axiomas. Por ejemplo, la aritmética de Peano se basa en un pequeño conjunto de axiomas a partir de los cuales se pueden inferir todas las propiedades esenciales de los números naturales mediante razonamiento deductivo.
Razonamiento no deductivo
El razonamiento no deductivo es una forma importante de razonamiento lógico además del razonamiento deductivo. Ocurre en forma de inferencias extraídas de premisas para llegar y respaldar una conclusión, al igual que su contraparte deductiva. El sello distintivo del razonamiento no deductivo es que este apoyo es falible. Esto significa que si las premisas son verdaderas, es más probable, pero no seguro, que la conclusión también lo sea. Entonces, para un argumento no deductivo, es posible que todas sus premisas sean verdaderas mientras que su conclusión sigue siendo falsa. Existen varios tipos de razonamiento no deductivo, como el razonamiento inductivo, abductivo y analógico. El razonamiento no deductivo es más común en la vida cotidiana que el razonamiento deductivo.
El razonamiento no deductivo es ampliativo y anulable. A veces, los términos razonamiento no deductivo, razonamiento ampliativo y razonamiento anulable se utilizan como sinónimos aunque existan ligeras diferencias en su significado. El razonamiento no deductivo es ampliativo en el sentido de que llega a información que aún no está presente en las premisas. El razonamiento deductivo, por el contrario, no es ampliativo ya que sólo extrae información que ya está presente en las premisas sin añadir ninguna información adicional. Entonces, con el razonamiento no deductivo, uno puede aprender algo nuevo que no sabía antes. Pero el hecho de que se agregue nueva información significa que esta información adicional puede ser falsa. Ésta es la razón por la que el razonamiento no deductivo no es tan seguro como el razonamiento deductivo.
Un aspecto estrechamente relacionado es que el razonamiento no deductivo es anulable o no monótono. Esto significa que es posible que uno tenga que retirar una conclusión al conocer nueva información. Por ejemplo, si todos los pájaros que una persona ha visto hasta ahora pueden volar, esta persona está justificada para llegar a la conclusión inductiva de que todos los pájaros vuelan. Esta conclusión es revocable porque el razonador puede tener que revisarla al enterarse de que los pingüinos son aves que no vuelan.
Inductivo

El razonamiento inductivo comienza a partir de un conjunto de casos individuales y utiliza la generalización para llegar a una ley universal que gobierna todos los casos. Algunos teóricos utilizan el término en un sentido muy amplio para incluir cualquier forma de razonamiento no deductivo, incluso si no implica ninguna generalización. En un sentido más estricto, puede definirse como "el proceso de inferir una ley o principio general a partir de observaciones de casos particulares". Por ejemplo, partiendo de la observación empírica de que "todos los cuervos que he visto hasta ahora son negros", se puede utilizar el razonamiento inductivo para inferir que "todos los cuervos son negros". En una forma ligeramente más débil, la inducción también se puede utilizar para inferir una conclusión individual sobre un caso concreto, por ejemplo, que "el próximo cuervo que veré es negro". El razonamiento inductivo está estrechamente relacionado con el razonamiento estadístico y el razonamiento probabilístico. Como otras formas de razonamiento no deductivo, la inducción no es segura. Esto significa que las premisas respaldan la conclusión haciéndola más probable pero no aseguran su verdad. En este sentido, la conclusión de una inferencia inductiva contiene información nueva que aún no se encuentra en las premisas.
Varios aspectos de las premisas son importantes para garantizar que ofrezcan un apoyo significativo a la conclusión. En este sentido, el tamaño de la muestra debe ser grande para garantizar que se consideren muchos casos individuales antes de llegar a la conclusión. Un factor íntimamente relacionado es que la muestra sea aleatoria y representativa. Esto significa que incluye una selección justa y equilibrada de personas con diferentes características clave. Por ejemplo, al hacer una generalización sobre los seres humanos, la muestra debe incluir miembros de diferentes razas, géneros y grupos de edad. Gran parte del razonamiento en la vida cotidiana es inductivo. Por ejemplo, al predecir cómo reaccionará una persona ante una situación, se puede emplear el razonamiento inductivo basándose en cómo reaccionó la persona anteriormente en circunstancias similares. Desempeña un papel igualmente central en las ciencias, que a menudo comienzan con muchas observaciones particulares y luego aplican el proceso de generalización para llegar a una ley universal.
Un tema bien conocido en el campo del razonamiento inductivo es el llamado problema de la inducción. Se trata de la cuestión de si alguien está justificado o por qué para creer en las conclusiones de las inferencias inductivas. Este problema fue planteado inicialmente por David Hume, quien sostiene que los acontecimientos futuros no tienen por qué parecerse a observaciones pasadas. En este sentido, el razonamiento inductivo sobre acontecimientos futuros parece descansar en el supuesto de que la naturaleza sigue siendo uniforme.
Abductivo
El razonamiento abductivo generalmente se entiende como una inferencia de una observación a un hecho que explica esta observación. Inferir que ha llovido tras ver que las calles están mojadas es un ejemplo. A menudo, la expresión "inferencia hacia la mejor explicación" se utiliza como sinónimo. Esta expresión subraya que normalmente hay muchas explicaciones posibles para un mismo hecho y que el razonador sólo debe inferir la mejor explicación. Por ejemplo, un tsunami también podría explicar por qué las calles están mojadas, pero ésta no suele ser la mejor explicación. Como forma de razonamiento no deductivo, la abducción no garantiza la verdad de la conclusión incluso si las premisas son verdaderas.
Cuanto más plausible es la explicación, más fuerte la respaldan las premisas. En este sentido, es importante que la explicación sea sencilla, es decir, que no incluya afirmaciones innecesarias y que sea coherente con el conocimiento establecido. Otros criterios centrales para una buena explicación son que se ajuste a hechos observados y comúnmente conocidos y que sea relevante, precisa y no circular. Idealmente, la explicación debería ser verificable mediante evidencia empírica. Si la explicación implica afirmaciones extraordinarias, entonces requiere pruebas muy sólidas.

El razonamiento abductivo juega un papel central en la ciencia cuando los investigadores descubren fenómenos inexplicables. En este caso, suelen recurrir a una forma de conjetura para llegar a principios generales que puedan explicar las observaciones. Luego, las hipótesis se prueban y comparan para descubrir cuál proporciona la mejor explicación. Esto se aplica particularmente a los casos de razonamiento causal que intentan descubrir la relación entre causas y efectos. La abducción también es muy común en la vida cotidiana. Se utiliza allí de forma similar pero menos sistemática. Esto se relaciona, por ejemplo, con la confianza que la gente deposita en lo que dicen los demás. La mejor explicación de por qué una persona afirma algo suele ser que lo cree y tiene pruebas de ello. Esta forma de razonamiento abductivo es relevante para explicar por qué uno normalmente confía en lo que dicen otras personas, aunque esta inferencia generalmente no se hace de manera explícita. Algo similar sucede cuando la afirmación del hablante es ambigua y la audiencia intenta descubrir y explicar lo que el hablante podría haber querido decir. El razonamiento abductivo también es común en medicina cuando un médico examina los síntomas de su paciente para llegar a un diagnóstico de su causa subyacente.
Analógica
(feminine)
El razonamiento analógico implica la comparación de dos sistemas en relación con su similitud. Comienza a partir de información sobre un sistema e infiere información sobre otro sistema en función de la semejanza entre los dos sistemas. Expresados esquemáticamente, los argumentos por analogía tienen la siguiente forma: (1) a es similar a b; (2) a tiene la característica F; (3) por lo tanto, b probablemente también tenga la característica F. El razonamiento analógico se puede utilizar, por ejemplo, para inferir información sobre humanos a partir de experimentos médicos con animales: (1) las ratas son similares a los humanos; (2) las píldoras anticonceptivas afectan el desarrollo del cerebro de las ratas; (3) por lo tanto, también pueden afectar el desarrollo del cerebro de los humanos.
A través del razonamiento analógico, el conocimiento se puede transferir de una situación o dominio a otro. Los argumentos por analogía respaldan su conclusión, pero no garantizan su verdad. Su fuerza depende de varios factores. Cuanto más similares sean los sistemas, más probable será que una característica dada de un objeto también caracterice al otro objeto. Otro factor se refiere no sólo al grado de similitud sino también a su relevancia. Por ejemplo, una fresa artificial hecha de plástico puede ser similar a una fresa real en muchos aspectos, incluida la forma, el color y la estructura de la superficie. Pero estas similitudes son irrelevantes para saber si la fresa artificial tiene un sabor tan dulce como la real.
El razonamiento analógico juega un papel central en la resolución de problemas, la toma de decisiones y el aprendizaje. Se puede utilizar tanto para características físicas simples como para ideas abstractas complejas. En ciencia, las analogías se utilizan a menudo en modelos para comprender fenómenos complejos de una manera sencilla. Por ejemplo, el modelo de Bohr explica las interacciones de las partículas subatómicas por analogía con la forma en que los planetas giran alrededor del sol.
Falacias
Una falacia es un argumento incorrecto o una forma de razonamiento defectuosa. Esto significa que las premisas no proporcionan apoyo suficiente o nulo para la conclusión. Las falacias a menudo parecen correctas en la primera impresión y, por lo tanto, inducen a la gente a aceptarlas y utilizarlas. En lógica, el término "falacia" no significa que la conclusión sea falsa. Más bien, sólo significa que se cometió algún tipo de error en el camino para llegar a la conclusión. Un argumento puede ser una falacia incluso si, por un accidente fortuito, la conclusión es verdadera. Fuera del campo de la lógica, el término "falacia" A veces se usa en un sentido ligeramente diferente para una creencia o teoría falsa y no para un argumento.
Las falacias generalmente se dividen en falacias formales e informales. Las falacias formales se expresan en un lenguaje formal y suelen pertenecer al razonamiento deductivo. Su error reside en la forma lógica del argumento, es decir, que no sigue una regla de inferencia válida. Una falacia formal muy conocida es afirmar el consecuente. Tiene la siguiente forma: (1) q; (2) si p entonces q; (3) por lo tanto p. Esta falacia se comete, por ejemplo, cuando una persona argumenta que "los ladrones entraron por la puerta principal" basado en las premisas "los ladrones forzaron la cerradura" y "si los ladrones entraron por la puerta principal, forzaron la cerradura". Esta falacia es similar a la regla válida de inferencia conocida como modus ponens. Es defectuoso porque la primera premisa y la conclusión están invertidas. Otras falacias formales bien conocidas son negar el antecedente, afirmar una disyunción, negar una conjunción y la falacia del tercero no distribuido.
Las falacias informales se expresan en lenguaje natural. Su principal defecto normalmente no reside en la forma del argumento sino que tiene otras fuentes, como su contenido o contexto. Algunas falacias informales, como algunos casos de falsos dilemas y falacias del hombre de paja, incluso implican un razonamiento deductivo correcto en el nivel formal. El contenido de un argumento es la idea que en él se expresa. Por ejemplo, un falso dilema es una falacia informal que se basa en un error en una de las premisas. La premisa errónea simplifica demasiado la realidad: afirma que las cosas son de una manera u otra pero ignoran muchas otras alternativas viables. Los políticos suelen utilizar falsos dilemas cuando afirman que o se acepta su propuesta o habrá consecuencias nefastas. Estas afirmaciones suelen ignorar que existen varias alternativas para evitar esas consecuencias, es decir, que su propuesta no es la única solución viable.
La falacia del hombre de paja es otra falacia informal. Su error ocurre en el nivel del contexto. Consiste en tergiversar la opinión de un oponente y luego refutar esa opinión. La refutación misma suele ser correcta, pero el error reside en la suposición falsa de que el oponente en realidad defiende este punto de vista. Por ejemplo, un cabildero del alcohol puede responder a la sugerencia de prohibir los anuncios de alcohol en la televisión afirmando que es imposible hacer que la gente deje de beber alcohol. Se trata de una falacia del hombre de paja, ya que la sugerencia era simplemente prohibir la publicidad y no detener por completo el consumo de alcohol.
Las expresiones ambiguas y vagas en el lenguaje natural son a menudo responsables del razonamiento defectuoso en las falacias informales. Por ejemplo, este es el caso de las falacias de ambigüedad, como el argumento "(1) las plumas son ligeras; (2) la luz se opone a la oscuridad; (3) por lo tanto las plumas se oponen a la oscuridad". El error se encuentra en el término ambiguo "ligero", que tiene un significado en la primera premisa ("no pesado") y un significado diferente en la segunda premisa ("visible radiación electromagnética").
Como habilidad
Algunos teóricos analizan el razonamiento lógico en un sentido muy amplio que incluye su papel como una habilidad amplia responsable del pensamiento de alta calidad. En este sentido, equivale aproximadamente al pensamiento crítico e incluye la capacidad de seleccionar y aplicar las reglas lógicas apropiadas a situaciones específicas. Abarca una gran variedad de habilidades además de sacar conclusiones a partir de premisas. Algunos ejemplos son comprender una posición, generar y evaluar razones a favor y en contra de ella, así como evaluar críticamente si se acepta o rechaza cierta información. Se trata de emitir juicios y sacar conclusiones después de una evaluación cuidadosa y, en este sentido, contrasta con los juicios precipitados y acríticos y las corazonadas. Otras habilidades básicas vinculadas al razonamiento lógico son evaluar las razones antes de aceptar una afirmación y buscar nueva información si se necesita más para llegar a una conclusión confiable. También incluye la capacidad de considerar diferentes cursos de acción y comparar las ventajas y desventajas de sus consecuencias, utilizar el sentido común y evitar inconsistencias. Las habilidades responsables del razonamiento lógico se pueden aprender, entrenar y mejorar.
El razonamiento lógico es relevante tanto a nivel teórico como práctico. A nivel teórico, ayuda a disminuir el número de creencias falsas. Un aspecto central se refiere a las habilidades utilizadas para distinguir hechos de meras opiniones, como el proceso de encontrar y evaluar razones a favor y en contra de una posición para llegar a la propia conclusión. Esto incluye ser capaz de diferenciar entre fuentes de información confiables y no confiables. Esto es importante para un razonamiento eficaz, ya que a menudo es necesario confiar en la información proporcionada por otras personas en lugar de comprobar cada hecho por uno mismo. De esta manera, el razonamiento lógico puede ayudar a la persona a evitar los efectos de la propaganda o ser manipulada por otros. Cuando falta información importante, a menudo es mejor suspender el juicio que sacar conclusiones precipitadas. En este sentido, el razonamiento lógico debe ser escéptico y abierto al mismo tiempo.
En el nivel práctico, el razonamiento lógico se refiere a la cuestión de tomar decisiones racionales y efectivas. Para muchas decisiones de la vida real, el agente dispone de varios cursos de acción. Para cada acción posible, puede haber razones contradictorias, algunas a favor y otras en contra. En tales casos, el razonamiento lógico incluye sopesar los posibles beneficios y desventajas, así como considerar su probabilidad para llegar a una decisión equilibrada que tenga en cuenta todos los aspectos. Por ejemplo, cuando una persona se queda sin agua potable en medio de un viaje de senderismo, podría emplear las habilidades asociadas con el razonamiento lógico para decidir si hervir y beber agua de un arroyo que podría contener microorganismos peligrosos en lugar de interrumpir el viaje. y camine de regreso al estacionamiento. Esto podría incluir considerar factores como evaluar qué tan peligrosos son los microorganismos y la probabilidad de que sobrevivan al procedimiento de ebullición. También puede implicar recopilar información relevante para realizar estas evaluaciones, por ejemplo, preguntando a otros excursionistas.
El tiempo también juega un papel central en el razonamiento lógico. Si a uno le falta información importante, a menudo es mejor retrasar la decisión y buscar nueva información antes de llegar a una conclusión. Por otro lado, si la decisión es urgente, el razonamiento lógico puede implicar tomar una decisión rápida basada en la evidencia actualmente disponible, incluso si es muy limitada. Por ejemplo, si un amigo grita "¡Agáchate!" Durante un partido de béisbol, la respuesta más lógica puede ser confiar ciegamente en ellos y agacharse en lugar de exigir una explicación o investigar qué pudo haber provocado su exclamación. En términos generales, cuanto menos tiempo haya, más importante será confiar en las intuiciones y las corazonadas. Por otra parte, si hay más tiempo, resulta importante examinar las ambigüedades y evaluar la información contradictoria.