Radiosidad (gráficos por computadora)

Escena realizada con RRV (simple implementación del renderizador de radiosidad basado en OpenGL) 79a iteración.

La caja Cornell, renderizada con y sin radio por BMRT

En gráficos 3D por computadora, la radiosidad es una aplicación del método de elementos finitos para resolver la ecuación de representación de escenas con superficies que reflejan la luz de manera difusa. A diferencia de los métodos de representación que usan algoritmos de Monte Carlo (como el seguimiento de rutas), que manejan todo tipo de rutas de luz, la radiosidad típica solo tiene en cuenta las rutas (representadas por el código "LD*E") que dejan una fuente de luz y se reflejan de forma difusa un cierto número de veces (posiblemente cero) antes de llegar al ojo. La radiosidad es un algoritmo de iluminación global en el sentido de que la iluminación que llega a una superficie no solo proviene directamente de las fuentes de luz, sino también de otras superficies que reflejan la luz. La radiosidad es independiente del punto de vista, lo que aumenta los cálculos involucrados, pero los hace útiles para todos los puntos de vista.

Los métodos de radiosidad se desarrollaron por primera vez alrededor de 1950 en el campo de la ingeniería de la transferencia de calor. Más tarde, investigadores de la Universidad de Cornell y la Universidad de Hiroshima los refinaron específicamente para el problema de renderizar gráficos por computadora en 1984.

Los motores de radiosidad comerciales notables son Enlighten de Geomerics (usado para juegos como Battlefield 3 y Need for Speed: The Run); 3ds máximo; forma•Z; LightWave 3D y el sistema de animación de imágenes eléctricas.

Características visuales

Diferencia entre iluminación directa estándar sin sombra penumbra, y radiosidad con sombra penumbra

La inclusión de cálculos de radiosidad en el proceso de renderizado a menudo aporta un elemento adicional de realismo a la escena final, debido a la forma en que imita los fenómenos del mundo real. Considere una escena de habitación simple.

La imagen de la izquierda se renderizó con un típico renderizador de iluminación directa. Hay tres tipos de iluminación en esta escena que han sido elegidos y colocados específicamente por el artista en un intento de crear una iluminación realista: iluminación puntual con sombras (colocada fuera de la ventana para crear la luz que incide en el suelo), la iluminación ambiental (sin la cual cualquier parte de la habitación que no esté directamente iluminada por una fuente de luz quedaría totalmente a oscuras) y la iluminación omnidireccional sin sombras (para reducir la monotonía de la iluminación ambiental).

La imagen de la derecha se renderizó usando un algoritmo de radiosidad. Sólo hay una fuente de luz: una imagen del cielo colocada fuera de la ventana. Se marca la diferencia. La habitación brilla con luz. Las sombras suaves son visibles en el piso y los efectos de iluminación sutiles se notan alrededor de la habitación. Además, el color rojo de la alfombra se ha difuminado en las paredes grises, dándoles un aspecto ligeramente cálido. Ninguno de estos efectos fue elegido o diseñado específicamente por el artista.

Resumen del algoritmo de radiosidad

Las superficies de la escena a renderizar se dividen cada una en una o más superficies más pequeñas (parches). Se calcula un factor de vista (también conocido como factor de forma) para cada par de parches; es un coeficiente que describe qué tan bien los parches pueden verse entre sí. Los parches que están lejos unos de otros, o que están orientados en ángulos oblicuos entre sí, tendrán factores de visualización más pequeños. Si hay otros parches en el camino, el factor de visualización se reducirá o será cero, dependiendo de si la oclusión es parcial o total.

Los factores de visualización se utilizan como coeficientes en un sistema lineal de ecuaciones de representación. Resolver este sistema produce la radiosidad, o brillo, de cada parche, teniendo en cuenta las interreflexiones difusas y las sombras suaves.

La radiosidad progresiva resuelve el sistema de forma iterativa con valores de radiosidad intermedios para el parche, correspondientes a los niveles de rebote. Es decir, después de cada iteración, sabemos cómo se ve la escena después de un ligero rebote, después de dos pases, dos rebotes, etc. Esto es útil para obtener una vista previa interactiva de la escena. Además, el usuario puede detener las iteraciones una vez que la imagen se vea lo suficientemente bien, en lugar de esperar a que el cálculo converja numéricamente.

A medida que el algoritmo se itera, la luz se puede ver para fluir en la escena, ya que se computan múltiples bonces. Los parches individuales son visibles como cuadrados en las paredes y el suelo.

Otro método común para resolver la ecuación de radiosidad es "disparar radiosidad" que resuelve iterativamente la ecuación de radiosidad "disparando" luz del parche con más energía en cada paso. Después de la primera pasada, solo se iluminarán los parches que estén en la línea de visión directa de un parche emisor de luz. Después del segundo pase, se iluminarán más parches a medida que la luz comience a rebotar alrededor de la escena. La escena continúa haciéndose más brillante y finalmente alcanza un estado estable.

Formulación matemática

El método básico de radiosidad tiene su base en la teoría de la radiación térmica, ya que la radiosidad se basa en calcular la cantidad de energía luminosa transferida entre superficies. Para simplificar los cálculos, el método supone que toda la dispersión es perfectamente difusa. Las superficies suelen discretizarse en elementos cuadriláteros o triangulares sobre los que se define una función polinomial por partes.

Después de este desglose, la cantidad de transferencia de energía luminosa se puede calcular utilizando la reflectividad conocida del parche reflectante, combinada con el factor de vista de los dos parches. Esta cantidad adimensional se calcula a partir de la orientación geométrica de dos parches y se puede considerar como la fracción del área total de emisión posible del primer parche que está cubierta por el segundo.

Más correctamente, la radiosidad B es la energía por unidad de área que sale de la superficie del parche por intervalo de tiempo discreto y es la combinación de energía emitida y reflejada:

B()x)dA=E()x)dA+*** *** ()x)dA∫ ∫ SB()x.)1π π r2#⁡ ⁡ Silencio Silencio x#⁡ ⁡ Silencio Silencio x.⋅ ⋅ Vis()x,x.)dA.{displaystyle B(x),dA=E(x),dA+rho (x),dAint _{S}B(x'){frac {1}{pi r^{2}}cos theta _{x}cos theta _{x'}cdot mathrm {Vis} (x,x} {d} A'

donde:

• B(x)_i dA_i es la energía total dejando una pequeña área dA_i alrededor de un punto x.
• E(x)_i dA_i es la energía emitida.
• ρ(x) es la reflectividad del punto, dando energía reflejada por área unidad multiplicando por la energía del incidente por área unidad (la energía total que llega de otros parches).
• S denota que la variable de integración x ' corre sobre todas las superficies de la escena
• r es la distancia entre x y x '
• Silencio_x y θ_{x '} son los ángulos entre la unión de línea x y x ' y vectores normales a la superficie x y x ' respectivamente.
• Vis(x,x ' ) es una función de visibilidad, definida para ser 1 si los dos puntos x y x ' son visibles entre sí, y 0 si no lo son.

El factor de forma geométrica (o "ángulo sólido proyectado") F_ij.

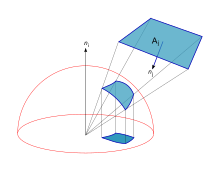
F_ij se puede obtener proyectando el elemento A_j sobre la superficie de un hemisferio unitario, y luego proyectando que a su vez en un círculo unitario alrededor del punto de interés en el plano A_i. El factor de forma es entonces igual a la proporción del círculo de unidad cubierto por esta proyección.

Los factores de forma obedecen a la relación reciprocidad A_iF_ij = A_jF_ji

Si las superficies se aproximan mediante un número finito de parches planos, cada uno de los cuales se considera que tiene una radiosidad B_i y una reflectividad ρ_i, la ecuación anterior da la ecuación de radiosidad discreta,

Bi=Ei+*** *** i.. j=1nFijBj{displaystyle B_{i}=E_{i}+rho ¿Qué? ¿Qué?

donde F_ij es el factor de vista geométrico para la radiación que sale de j y golpea el parche i.

Esta ecuación se puede aplicar a cada parche. La ecuación es monocromática, por lo que la representación de la radiosidad del color requiere un cálculo para cada uno de los colores requeridos.

Métodos de solución

La ecuación se puede resolver formalmente como una ecuación matricial, para dar la solución vectorial:

B=()I− − *** *** F)− − 1E{displaystyle B=(I-rho F)^{-1}E;}

Esto proporciona el "rebote infinito" solución para B directamente. Sin embargo, el número de cálculos para calcular la solución de matriz se escala según n³, donde n es el número de parches. Esto se vuelve prohibitivo para valores realmente grandes de n.

En cambio, la ecuación se puede resolver más fácilmente de forma iterativa, aplicando repetidamente la fórmula de actualización de rebote único anterior. Formalmente, esta es una solución de la ecuación matricial por iteración de Jacobi. Debido a que las reflectividades ρ_i son menores que 1, este esquema converge rápidamente y, por lo general, requiere solo unas pocas iteraciones para producir una solución razonable. También se pueden usar otros métodos iterativos estándar para soluciones de ecuaciones matriciales, por ejemplo, el método de Gauss-Seidel, donde los valores actualizados para cada parche se usan en el cálculo tan pronto como se calculan, en lugar de que todos se actualicen sincrónicamente al final de cada uno. barrer. La solución también se puede ajustar para iterar sobre cada uno de los elementos de envío a su vez en su ciclo principal más externo para cada actualización, en lugar de cada uno de los parches de recepción. Esto se conoce como la variante disparar del algoritmo, a diferencia de la variante reunir. Usando la reciprocidad del factor de visualización, A_i F_ij = A _j F_ji, la ecuación de actualización también se puede reescribir en términos del factor de visualización F_ji visto por cada parche envío A_j:

AiBi=AiEi+*** *** i.. j=1nAjBjFji{displaystyle ¿Qué? ¿Qué? ¿Qué?

Esto a veces se conoce como el "poder" formulación, ya que ahora es la potencia total transmitida de cada elemento que se está actualizando, en lugar de su radiosidad.

El factor de visualización F_ij se puede calcular de varias formas. Los primeros métodos usaban un hemicubo (un cubo imaginario centrado en la primera superficie a la que se proyectaba la segunda superficie, ideado por Michael F. Cohen y Donald P. Greenberg en 1985). La superficie del hemicubo se dividió en cuadrados similares a píxeles, para cada uno de los cuales se puede calcular analíticamente un factor de vista. Luego, el factor de forma completo podría aproximarse sumando la contribución de cada uno de los cuadrados similares a píxeles. La proyección sobre el hemicubo, que podría adaptarse a partir de los métodos estándar para determinar la visibilidad de los polígonos, también resolvió el problema de los parches intermedios que oscurecían parcialmente los que estaban detrás.

Sin embargo, todo esto fue bastante costoso desde el punto de vista computacional, porque idealmente se deben derivar factores de forma para cada par posible de parches, lo que lleva a un aumento cuadrático en el cálculo a medida que aumenta la cantidad de parches. Esto se puede reducir un poco mediante el uso de un árbol de partición de espacio binario para reducir la cantidad de tiempo dedicado a determinar qué parches están completamente ocultos para los demás en escenas complejas; pero aun así, el tiempo dedicado a determinar el factor de forma normalmente se escala como n log n. Los nuevos métodos incluyen la integración adaptativa.

Enfoques de muestreo

Los factores de forma F_ij en sí mismos no son explícitamente necesarios en ninguna de las ecuaciones de actualización; ni para estimar la intensidad total Σ_j F_ij B_j recogida de la vista completa, ni para estimar cómo se distribuye la potencia A_j B_j que se está radiando. En cambio, estas actualizaciones se pueden estimar mediante métodos de muestreo, sin tener que calcular los factores de forma explícitamente. Desde mediados de la década de 1990, estos enfoques de muestreo han sido los métodos más utilizados para los cálculos prácticos de radiosidad.

La intensidad recopilada se puede estimar generando un conjunto de muestras en el círculo unitario, levantándolas sobre el hemisferio y luego viendo cuál era la radiosidad del elemento en el que se habría originado un rayo entrante en esa dirección. La estimación de la intensidad total acumulada es solo el promedio de las radiosidades descubiertas por cada rayo. De manera similar, en la formulación de potencia, la potencia se puede distribuir generando un conjunto de rayos a partir del elemento radiante de la misma manera y extendiendo la potencia para que se distribuya equitativamente entre cada elemento que golpea un rayo.

Esta es esencialmente la misma distribución que muestrearía un programa de rastreo de ruta al rastrear un paso de reflexión difusa; o que un programa de trazado de rayos bidireccional tomaría muestras para lograr un paso de reflexión difusa hacia adelante cuando el mapeo de la fuente de luz hacia adelante. Por lo tanto, el enfoque de muestreo representa hasta cierto punto una convergencia entre las dos técnicas, la diferencia clave es que la técnica de radiosidad tiene como objetivo construir un mapa suficientemente preciso de la radiación de todas las superficies en la escena, en lugar de solo una representación de la corriente. vista.

Reducción del tiempo de cálculo

Aunque en su forma básica se supone que la radiosidad tiene un aumento cuadrático en el tiempo de cálculo con geometría añadida (superficies y parches), este no tiene por qué ser el caso. El problema de la radiosidad se puede reformular como un problema de representación de una escena mapeada con textura. En este caso, el tiempo de cálculo aumenta solo linealmente con la cantidad de parches (ignorando problemas complejos como el uso de caché).

Siguiendo el entusiasmo comercial por las imágenes mejoradas con radiosidad, pero antes de la estandarización del cálculo rápido de radiosidad, muchos arquitectos y artistas gráficos utilizaron una técnica denominada vagamente radiosidad falsa. Al oscurecer las áreas de los mapas de textura correspondientes a las esquinas, las juntas y los huecos, y aplicarlos a través de la autoiluminación o el mapeo difuso, se podría crear un efecto similar a la radiosidad de la interacción del parche con un renderizador de línea de exploración estándar (cf. oclusión ambiental).

La radiosidad estática y precalculada se puede mostrar en tiempo real a través de Lightmaps en las computadoras de escritorio actuales con hardware de aceleración de gráficos estándar.

Ventajas

Un moderno render de la tetera de Utah. La radiosidad se utilizó para toda iluminación difusa en esta escena.

Una de las ventajas del algoritmo Radiosity es que es relativamente simple de explicar e implementar. Esto lo convierte en un algoritmo útil para enseñar a los estudiantes sobre algoritmos de iluminación global. Un renderizador de iluminación directa típico ya contiene casi todos los algoritmos (transformaciones de perspectiva, mapeo de texturas, eliminación de superficies ocultas) necesarios para implementar la radiosidad. No se requiere una gran comprensión de las matemáticas para comprender o implementar este algoritmo.

Limitaciones

Los métodos típicos de radiosidad solo tienen en cuenta las trayectorias de luz de la forma LD*E, es decir, trayectorias que comienzan en una fuente de luz y realizan múltiples rebotes difusos antes de llegar al ojo. Aunque existen varios enfoques para integrar otros efectos de iluminación, como reflejos especulares y brillantes, los métodos basados en radiosidad generalmente no se utilizan para resolver la ecuación de renderizado completa.

La radiosidad básica también tiene problemas para resolver cambios repentinos en la visibilidad (p. ej., sombras con bordes definidos) porque la discretización regular gruesa en elementos constantes por partes corresponde a un filtro de caja de paso bajo del dominio espacial. El mallado de discontinuidades [1] utiliza el conocimiento de los eventos de visibilidad para generar una discretización más inteligente.

Confusión sobre la terminología

La radiosidad fue quizás el primer algoritmo de renderizado de uso generalizado que tuvo en cuenta la iluminación indirecta difusa. Los algoritmos de renderizado anteriores, como el trazado de rayos de estilo Whitted, eran capaces de calcular efectos como reflejos, refracciones y sombras, pero a pesar de ser fenómenos altamente globales, estos efectos no se denominaban comúnmente "iluminación global".; En consecuencia, los términos "interreflexión difusa" y "radiosidad" ambos se confundieron con "iluminación global" en el lenguaje popular. Sin embargo, los tres son conceptos distintos.

El método de radiosidad, en el contexto de los gráficos por computadora, se deriva (y es fundamentalmente el mismo) del método de radiosidad en la transferencia de calor. En este contexto, la radiosidad es el flujo radiativo total (tanto reflejado como reirradiado) que sale de una superficie; esto también se conoce a veces como excitación radiante. El cálculo de la radiosidad, en lugar de las temperaturas superficiales, es un aspecto clave del método de radiosidad que permite aplicar métodos de matrices lineales al problema.