Radio de convergencia

En matemáticas, la radio de convergencia de una serie de potencia es el radio del disco más grande en el centro de la serie en la que converge la serie. Es un número real no negativo o ${displaystyle infty }$. Cuando es positivo, la serie de potencia converge absolutamente y uniformemente en conjuntos compactos dentro del disco abierto de radio igual al radio de convergencia, y es la serie Taylor de la función analítica a la que converge. En caso de múltiples singularidades de una función (las singularidades son los valores del argumento para el cual no se define la función), el radio de convergencia es el más corto o mínimo de todas las distancias respectivas (que son todos números no negativos) calculadas desde el centro del disco de convergencia a las respectivas singularidades de la función.

Definición

Para una serie de potencias f definida como:

${displaystyle f(z)=sum _{n=0}{infty }c_{n}(z-a)^{n}$

dónde

• a es una constante compleja, el centro del disco de convergencia,
• c_n es n- el coeficiente complejo y
• z es una variable compleja.

El radio de convergencia r es un número real no negativo o ${displaystyle infty }$ tal que la serie converge si

${displaystyle Silencioz-a escondidar}$

y diverge si

${displaystyle Silencioz-a confidencial.}$

Algunos pueden preferir una definición alternativa, ya que la existencia es obvia:

${displaystyle r=sup left{Principio-a sobre la vida\ de la izquierda _{n=0}^{infty }c_{n}(z-a)^{n} Bien.$

En el límite, es decir, donde |z − a| = r, el comportamiento de la serie de potencias puede ser complicado y la serie puede converger para algunos valores de z y divergir para otros. El radio de convergencia es infinito si la serie converge para todos los números complejos z.

Encontrar el radio de convergencia

Dos casos surgen. El primer caso es teórico: cuando conoce todos los coeficientes ${displaystyle c_{n}$ entonces toma ciertos límites y encuentra el radio preciso de convergencia. El segundo caso es práctico: cuando construyes una solución de serie de energía de un problema difícil normalmente solo conocerás un número finito de términos en una serie de potencia, desde un par de términos hasta cien términos. En este segundo caso, extrapolar una parcela estima el radio de convergencia.

Radio teórico

El radio de convergencia se puede encontrar aplicando la prueba de la raíz a los términos de la serie. La prueba raíz usa el número

${displaystyle C=limsup _{nto infty }{sqrt[{n} { mint_{n}(z-a)^{n}}=limsup _{nto infty }left({sqrt[{n}] [Principalmente]$

"lim superior" denota el límite superior. La prueba de la raíz establece que la serie converge si C < 1 y diverge si C > 1. Se sigue que la serie de potencias converge si la distancia de z al centro a es menor que

${displaystyle r={frac {1}{nto infty }{n}{n} {n} {n} {n} {n}}}}}}}}} {n}}}}}}}} {n}}}}}} {n}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$

y diverge si la distancia excede ese número; este enunciado es el teorema de Cauchy-Hadamard. Tenga en cuenta que r = 1/0 se interpreta como un radio infinito, lo que significa que f es una función completa.

El límite involucrado en la prueba de la razón suele ser más fácil de calcular y, cuando ese límite existe, muestra que el radio de convergencia es finito.

${displaystyle r=lim _{ntoinfty}lefttención{frac {c_{n} {c_{n+1}} 'justo en la vida.}$

Esto se muestra a continuación. La prueba de la razón dice que la serie converge si

${displaystyle lim _{nto infty}{frac {c_{n+1}(z-a)}{n+1}Principi} {c_{n} {n} {n}} {n}}}}} {n}}} {n}}}} {n}}}} {n}}}$

Eso es equivalente a

${displaystyle tenciónz-a escondida {frac {1}{lim _{nto infty }{frac {c_{n+1} {fn}}}}=lim _{ntoinfty }left WordPress{frac {c_{n} {c_{n+1}} 'justo en la vida.}$

Estimación práctica del radio en el caso de coeficientes reales

Parcelas de la función ${displaystyle f(varepsilon)={frac {varepsilon (1+varepsilon ^{3}}{sqrt {1+2varepsilon }}}$
La línea verde sólida es el asintoto de línea recta en la parcela de Domb-Sykes, parcela (b), que intercepta el eje vertical en −2 y tiene una pendiente +1. Así hay una singularidad en ${displaystyle varepsilon =-1/2}$ y así el radio de convergencia es ${displaystyle r=1/2.}$

Normalmente, en aplicaciones científicas, sólo un número finito de coeficientes ${displaystyle c_{n}$ son conocidos. Típicamente, como ${displaystyle n}$ aumenta, estos coeficientes se asientan en un comportamiento regular determinado por la singularidad que limita radios más cercana. En este caso, se han desarrollado dos técnicas principales, sobre la base de que los coeficientes de una serie Taylor son aproximadamente exponenciales con relación ${displaystyle 1/r}$ Donde r es el radio de convergencia.

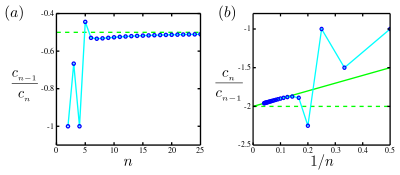
• El caso básico es cuando los coeficientes finalmente comparten un signo común o alternan en el signo. Como se señaló anteriormente en el artículo, en muchos casos el límite ${textstyle lim _{nto infty } {c_{n}/c_{n-1}}$ existe, y en este caso ${textstyle 1/r=lim _{nto infty } {c_{n}/c_{n-1}}$. Negativo ${displaystyle r}$ significa que la singularidad que limita la convergencia está en el eje negativo. Estimar este límite, trazando el ${displaystyle C_{n}/c_{n-1}$ versus ${displaystyle 1/n}$, y gráficamente extrapolar a ${displaystyle 1/n=0}$ (eficacia) ${displaystyle n=infty}$) a través de un ajuste lineal. La interceptación ${displaystyle 1/n=0}$ estima el recíproco del radio de convergencia, ${displaystyle 1/r}$. Esta trama se llama Domb-Sykes plot.
• El caso más complicado es cuando los signos de los coeficientes tienen un patrón más complejo. Mercer y Roberts propusieron el siguiente procedimiento. Definir la secuencia asociada
  $${displaystyle ¿Qué? {c_{n+1}c_{n-1}}quad n=3,4,5,ldots.}$$

  
  Parcela a los finitos muchos conocidos ${displaystyle B_{n}$ versus ${displaystyle 1/n}$, y gráficamente extrapolar a ${displaystyle 1/n=0}$ a través de un ajuste lineal. La interceptación ${displaystyle 1/n=0}$ estima el recíproco del radio de convergencia, ${displaystyle 1/r}$.
  Este procedimiento también estima otras dos características de la convergencia que limita la singularidad. Supongamos que la singularidad más cercana es de grado ${displaystyle p}$ y tiene ángulo ${displaystyle pm theta }$ al eje real. Entonces la pendiente del ajuste lineal dada arriba es ${displaystyle -(p+1)/r}$. Además, trama ${textstyle {frac}{2}left({frac} {c_{n-1}b_{n} {c_{n}}+{frac} {c_{n+1} {c_{n}}}right)}$ versus ${textstyle 1/n^{2}$, entonces un ajuste lineal extrapolado a ${textstyle 1/n^{2}=0}$ ha interceptado ${displaystyle cos theta }$.

Radio de convergencia en análisis complejo

Una serie de potencias con un radio de convergencia positivo se puede convertir en una función holomorfa tomando su argumento como una variable compleja. El radio de convergencia se puede caracterizar por el siguiente teorema:

El radio de convergencia de una serie de energía f centrado en un punto a es igual a la distancia desde a al punto más cercano donde f no se puede definir de una manera que lo hace holomorfo.

El conjunto de todos los puntos cuya distancia a a es estrictamente menor que el radio de convergencia se denomina disco de convergencia.

Un gráfico de las funciones explicadas en el texto: Aproximaciones en azul, círculo de convergencia en blanco

El punto más cercano significa el punto más cercano en el plano complejo, no necesariamente en la línea real, incluso si el centro y todos los coeficientes son reales. Por ejemplo, la función

${displaystyle f(z)={frac {1}{1+z^{2}}}$

no tiene singularidades en la línea real, ya ${displaystyle 1+z^{2}$ no tiene raíces reales. Su serie Taylor sobre 0 es dada por

${displaystyle sum _{n=0}{infty }(-1)^{n}z^{2n}$

La prueba de la raíz muestra que su radio de convergencia es 1. De acuerdo con esto, la función f(z) tiene singularidades en ±i, que están a una distancia 1 de 0.

Para una prueba de este teorema, vea analiticidad de funciones holomorfas.

Un ejemplo sencillo

La función arcotangente de la trigonometría se puede expandir en una serie de potencias:

${displaystyle arctan(z)=z-{frac {fnMicroc} {fnMicroc} {fnK} {5}} {fnMicroc} {Z^{7}}cdots.}$

Es fácil aplicar la prueba de la raíz en este caso para encontrar que el radio de convergencia es 1.

Un ejemplo más complicado

Considere esta serie de potencias:

${displaystyle {frac {z}{z}}=sum ¿Qué? ¡Vamos!$

donde los números racionales B_n son los números de Bernoulli. Puede ser engorroso tratar de aplicar la prueba de la razón para encontrar el radio de convergencia de esta serie. Pero el teorema del análisis complejo mencionado anteriormente resuelve rápidamente el problema. En z = 0, en efecto, no hay singularidad ya que la singularidad es removible. Por lo tanto, las únicas singularidades no eliminables se ubican en los otros puntos donde el denominador es cero. Solucionamos

${displaystyle E^{z}-1=0}$

recordando que si z = x + iy y e^iy = cos(y) + i sin(y) entonces

${displaystyle e^{z}=e^{x}e^{iy}=e^{x}(cos(y)+isin(y)}$

y luego toma x e y como reales. Dado que y es real, el valor absoluto de cos(y) + i sin(y ) es necesariamente 1. Por lo tanto, el valor absoluto de e^z puede ser 1 solo si e^x es 1; dado que x es real, eso sucede solo si x = 0. Por lo tanto, z es puramente imaginario y cos(y) + i sin(y) = 1. Dado que y es real, eso sucede solo si cos(y) = 1 y sin(y) = 0, de modo que y es un múltiplo entero de 2π. En consecuencia, los puntos singulares de esta función se encuentran en

z = un número entero no cero de 2πi.

Las singularidades más cercanas a 0, que es el centro de la expansión de la serie de potencias, están en ±2πi . La distancia desde el centro a cualquiera de esos puntos es 2π, por lo que el radio de convergencia es 2π.

Convergencia en el límite

Si la serie de potencias se expande alrededor del punto a y el radio de convergencia es r, entonces el conjunto de todos los puntos z tales que |z − a| = r es un círculo llamado límite del disco de convergencia. Una serie de potencias puede divergir en todos los puntos de la frontera, o divergir en algunos puntos y converger en otros, o converger en todos los puntos de la frontera. Además, incluso si la serie converge en todas partes en el límite (incluso uniformemente), no necesariamente converge de manera absoluta.

Ejemplo 1: La serie de potencias para la función f(z) = 1/(1 − z), expandido alrededor de z = 0, que es simplemente

${displaystyle sum _{n=0}{infty }z^{n} }$

tiene un radio de convergencia de 1 y diverge en todos los puntos de la frontera.

Ejemplo 2: La serie de potencias para g(z) = −ln(1 − z), expandido alrededor de z = 0, que es

${displaystyle sum _{n=1}{infty }{frac {1} {n}z^{n},}$

tiene un radio de convergencia de 1 y diverge para z = 1 pero converge para todos los demás puntos del límite. La función f(z) del Ejemplo 1 es la derivada de g(z).

Ejemplo 3: La serie de potencias

${displaystyle sum _{n=1} {infty}{frac {1}{n^{2}}} {n}} {n}} {n}}} {n}} {n}}}} {fn}}} {n}}} {n}}}}} {n}}}}}}}}}}}} {$

tiene un radio de convergencia de 1 y converge absolutamente en todas partes en el límite. Si h es la función representada por esta serie en el disco unitario, entonces la derivada de h(z ) es igual a g(z)/z con g del Ejemplo 2. Resulta descubra que h(z) es la función de dilogaritmo.

Ejemplo 4: La serie de potencias

${displaystyle sum {fn} {fn} {fn} {fn} {fn} {fn} {fn} {fn} {fn}} {fn}fn} {fn}fnfn}fn}fnfn}fnfnfncH00}cH00fn}fn}fn}fn}fn}cH00cH00fn}fn}cH00fn}cH00cH00cH00cH00cH00cH00cH00cH00fn}fn}fn}fn}fn}fn}cH00cH00cH00fn}fn}fn}fn}fn}cH00cH00cH00cH00cH00}cH00cH$

tiene un radio de convergencia de 1 y converge uniformemente en todo el límite | z| = 1, pero no converge absolutamente en el límite.

Tasa de convergencia

Si expandimos la función

${displaystyle sin x=sum _{n=0}{infty }{frac {(-1)^{n}{(2n+1)}}x^{2n+1}=x-{frac {x^{3}{3}}}+{frac {x^{5} {5}}}}-cdots {text{ for all }x}$

alrededor del punto x = 0, averiguamos que el radio de convergencia de esta serie es ${displaystyle infty }$ significa que esta serie converge para todos los números complejos. Sin embargo, en aplicaciones, a menudo se interesa en la precisión de una respuesta numérica. Tanto el número de términos como el valor en el que se va a evaluar la serie afectan la exactitud de la respuesta. Por ejemplo, si queremos calcular sin(0.1) exacto hasta cinco lugares decimales, sólo necesitamos los dos primeros términos de la serie. Sin embargo, si queremos la misma precisión para x = 1 debemos evaluar y resumir los primeros cinco términos de la serie. Para pecado(10), uno requiere los primeros 18 términos de la serie, y para sin(100) necesitamos evaluar los primeros 141 términos.

Entonces, para estos valores particulares, la convergencia más rápida de una expansión en serie de potencias está en el centro, y a medida que uno se aleja del centro de convergencia, la tasa de convergencia se ralentiza hasta que alcanza el límite (si existe) y cruza terminado, en cuyo caso la serie divergirá.

Abscisa de convergencia de una serie de Dirichlet

Un concepto análogo es la abscisa de convergencia de una serie de Dirichlet

${displaystyle sum _{n=1}{infty }{frac {a_{n} {fn}}}}$

Tal serie converge si la parte real de s es mayor que un número particular dependiendo de los coeficientes a_{n< /sub>: la abscisa de convergencia.}