Radiación termal
La radiación térmica es la radiación electromagnética generada por el movimiento térmico de las partículas en la materia. La radiación térmica se genera cuando el calor del movimiento de cargas en el material (electrones y protones en formas comunes de materia) se convierte en radiación electromagnética. Toda materia con una temperatura superior al cero absoluto emite radiación térmica. A temperatura ambiente, la mayor parte de la emisión está en el espectro infrarrojo (IR). El movimiento de partículas da como resultado una aceleración de carga u oscilación dipolar que produce radiación electromagnética.
La radiación infrarroja emitida por animales (detectable con una cámara infrarroja) y la radiación cósmica de fondo de microondas son ejemplos de radiación térmica.
Si un objeto de radiación cumple con las características físicas de un cuerpo negro en equilibrio termodinámico, la radiación se denomina radiación de cuerpo negro. La ley de Planck describe el espectro de radiación de cuerpo negro, que depende únicamente de la temperatura del objeto. La ley de desplazamiento de Wien determina la frecuencia más probable de la radiación emitida y la ley de Stefan-Boltzmann da la intensidad radiante.
La radiación térmica es también uno de los mecanismos fundamentales de transferencia de calor.
Resumen
La radiación térmica es la emisión de ondas electromagnéticas de toda la materia que tiene una temperatura superior al cero absoluto. La radiación térmica refleja la conversión de energía térmica en energía electromagnética. La energía térmica es la energía cinética de los movimientos aleatorios de átomos y moléculas en la materia. Toda la materia con una temperatura distinta de cero está compuesta de partículas con energía cinética. Estos átomos y moléculas están compuestos de partículas cargadas, es decir, protones y electrones. Las interacciones cinéticas entre las partículas de materia dan como resultado la aceleración de carga y la oscilación del dipolo. Esto da como resultado la generación electrodinámica de campos eléctricos y magnéticos acoplados, lo que da como resultado la emisión de fotones que irradian energía fuera del cuerpo. La radiación electromagnética, incluida la luz visible, se propagará indefinidamente en el vacío.
Las características de la radiación térmica dependen de varias propiedades de la superficie de la que emana, incluida su temperatura, su emisividad espectral, según lo expresado por la ley de Kirchhoff. La radiación no es monocromática, es decir, no consta de una sola frecuencia, sino que comprende un espectro continuo de energías de fotones, su espectro característico. Si el cuerpo radiante y su superficie están en equilibrio termodinámico y la superficie tiene una capacidad de absorción perfecta en todas las longitudes de onda, se caracteriza como un cuerpo negro. Un cuerpo negro es también un emisor perfecto. La radiación de tales emisores perfectos se llama radiación de cuerpo negro. La relación entre la emisión de cualquier cuerpo y la de un cuerpo negro es la emisividad del cuerpo, de modo que un cuerpo negro tiene una emisividad de unidad (es decir, uno).
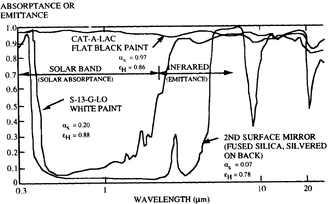
La capacidad de absorción, la reflectividad y la emisividad de todos los cuerpos dependen de la longitud de onda de la radiación. Debido a la reciprocidad, la absortividad y la emisividad para cualquier longitud de onda en particular son iguales en el equilibrio: un buen absorbente es necesariamente un buen emisor y un pobre absorbente es un mal emisor. La temperatura determina la distribución de la longitud de onda de la radiación electromagnética. Por ejemplo, la pintura blanca en el diagrama de la derecha es altamente reflectante para la luz visible (reflectividad de aproximadamente 0,80), por lo que parece blanca para el ojo humano debido a la luz solar reflejada, que tiene una longitud de onda máxima de aproximadamente 0,5 micrómetros. Sin embargo, su emisividad a una temperatura de aproximadamente -5 °C (23 °F), con una longitud de onda máxima de aproximadamente 12 micrómetros, es de 0,95. Así, a la radiación térmica aparece negro.
La ley de Planck describe la distribución de energía que emite un cuerpo negro con frecuencia variable. A cualquier temperatura dada, existe una frecuencia fmax en la que la potencia emitida es máxima. La ley de desplazamiento de Wien, y el hecho de que la frecuencia es inversamente proporcional a la longitud de onda, indica que la frecuencia pico fmax es proporcional a la temperatura absoluta T del cuerpo negro. La fotosfera del sol, a una temperatura de aproximadamente 6000 K, emite radiación principalmente en la porción visible (humana) del espectro electromagnético. La atmósfera de la Tierra es parcialmente transparente a la luz visible y la luz que llega a la superficie es absorbida o reflejada. La superficie de la Tierra emite la radiación absorbida, aproximándose al comportamiento de un cuerpo negro a 300 K con un pico espectral en fmax. En estas frecuencias más bajas, la atmósfera es en gran parte opaca y la radiación de la superficie de la Tierra es absorbida o dispersada por la atmósfera. Aunque alrededor del 10% de esta radiación se escapa al espacio, la mayor parte es absorbida y luego reemitida por los gases atmosféricos. Es esta selectividad espectral de la atmósfera la responsable del efecto invernadero planetario, que contribuye al calentamiento global y al cambio climático en general (pero también contribuye de manera crítica a la estabilidad climática cuando la composición y las propiedades de la atmósfera no cambian).
La bombilla de luz incandescente tiene un espectro que se superpone al espectro del cuerpo negro del sol y la tierra. Algunos de los fotones emitidos por el filamento de una bombilla de tungsteno a 3000 K se encuentran en el espectro visible. La mayor parte de la energía está asociada con fotones de longitudes de onda más largas; estos no ayudan a una persona a ver, pero aun así transfieren calor al medio ambiente, como se puede deducir empíricamente al observar una bombilla incandescente. Cada vez que se emite radiación EM y luego se absorbe, se transfiere calor. Este principio se utiliza en hornos de microondas, corte por láser y depilación por radiofrecuencia.
A diferencia de las formas de transferencia de calor por conducción y convección, la radiación térmica se puede concentrar en un punto diminuto mediante el uso de espejos reflectantes, de los que se aprovecha la energía solar de concentración. En lugar de espejos, las lentes de Fresnel también se pueden usar para concentrar energía radiante. (En principio, se puede usar cualquier tipo de lente, pero solo el diseño de lente Fresnel es práctico para lentes muy grandes). Se puede usar cualquier método para vaporizar rápidamente el agua en vapor utilizando la luz solar. Por ejemplo, la luz del sol reflejada en los espejos calienta la planta de energía solar PS10 y durante el día puede calentar el agua a 285 °C (558 K; 545 °F).
Efectos de superficie
Los colores más claros y también los blancos y las sustancias metálicas absorben menos luz de iluminación y, como resultado, se calientan menos; pero, por lo demás, el color hace poca diferencia en lo que respecta a la transferencia de calor entre un objeto a temperaturas cotidianas y su entorno, ya que las longitudes de onda dominantes emitidas no están ni cerca del espectro visible, sino más bien en el infrarrojo lejano. Las emisividades en esas longitudes de onda en gran medida no están relacionadas con las emisividades visuales (colores visibles); en el infrarrojo lejano, la mayoría de los objetos tienen altas emisividades. Así, excepto a la luz del sol, el color de la ropa hace poca diferencia en cuanto al calor; del mismo modo, el color de la pintura de las casas hace poca diferencia en cuanto al calor, excepto cuando la parte pintada está iluminada por el sol.
La principal excepción a esto son las superficies metálicas brillantes, que tienen bajas emisividades tanto en las longitudes de onda visibles como en el infrarrojo lejano. Tales superficies pueden usarse para reducir la transferencia de calor en ambas direcciones; un ejemplo de esto es el aislamiento multicapa utilizado para aislar naves espaciales.
Las ventanas de baja emisividad en las casas son una tecnología más complicada, ya que deben tener una baja emisividad en las longitudes de onda térmicas y permanecer transparentes a la luz visible.
Las nanoestructuras con propiedades de emitancia térmica espectralmente selectiva ofrecen numerosas aplicaciones tecnológicas para la generación y la eficiencia energética, por ejemplo, para el enfriamiento radiativo diurno de células fotovoltaicas y edificios. Estas aplicaciones requieren una alta emitancia en el rango de frecuencia correspondiente a la ventana de transparencia atmosférica en un rango de longitud de onda de 8 a 13 micras. Un emisor selectivo que irradia intensamente en este rango queda así expuesto al cielo despejado, lo que permite utilizar el espacio exterior como disipador de calor a muy baja temperatura.
La tecnología de refrigeración personalizada es otro ejemplo de una aplicación en la que la selectividad espectral óptica puede resultar beneficiosa. El enfriamiento personal convencional generalmente se logra a través de la conducción y convección de calor. Sin embargo, el cuerpo humano es un emisor muy eficiente de radiación infrarroja, lo que proporciona un mecanismo de enfriamiento adicional. La mayoría de los tejidos convencionales son opacos a la radiación infrarroja y bloquean la emisión térmica del cuerpo al medio ambiente. Se han propuesto telas para aplicaciones de enfriamiento personalizadas que permiten que la transmisión infrarroja atraviese directamente la ropa, mientras que son opacos en longitudes de onda visibles, lo que permite que el usuario permanezca más fresco.
Propiedades
Hay cuatro propiedades principales que caracterizan la radiación térmica (en el límite del campo lejano):
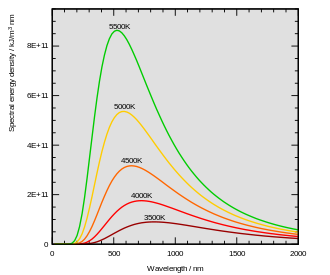
- La radiación térmica emitida por un cuerpo a cualquier temperatura consiste en una amplia gama de frecuencias. La distribución de frecuencia es dada por la ley de Planck de radiación de cuerpo negro para un emisor idealizado como se muestra en el diagrama en la parte superior.
- La frecuencia dominante (o color) de la radiación emitida cambia a frecuencias más altas a medida que aumenta la temperatura del emisor. Por ejemplo, a rojo caliente el objeto se irradia principalmente en las largas longitudes de onda (rojo y naranja) de la banda visible. Si se calienta más, también comienza a emitir cantidades discernibles de luz verde y azul, y la propagación de frecuencias en todo el rango visible hace que parezca blanco al ojo humano; es blanco caliente. Incluso a una temperatura blanca de 2000 K, el 99% de la energía de la radiación sigue en el infrarrojo. Esto está determinado por la ley de desplazamiento de Wien. En el diagrama el valor máximo de cada curva se mueve a la izquierda a medida que aumenta la temperatura.
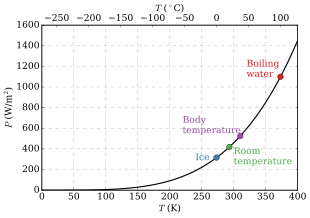
- La cantidad total de radiación de toda frecuencia aumenta abruptamente a medida que la temperatura aumenta; crece a medida que T4, donde T es la temperatura absoluta del cuerpo. Un objeto a la temperatura de un horno de cocina, aproximadamente el doble de la temperatura ambiente en la escala de temperatura absoluta (600 K vs. 300 K) irradia 16 veces más potencia por área unidad. Un objeto a la temperatura del filamento en una bombilla incandescente —aproximadamente 3000 K, o 10 veces la temperatura ambiente— irradia 10.000 veces más energía por área unidad. La intensidad radiativa total de un cuerpo negro aumenta como el cuarto poder de la temperatura absoluta, como lo expresa la ley Stefan-Boltzmann. En la parcela, el área bajo cada curva crece rápidamente a medida que aumenta la temperatura.
- La tasa de radiación electromagnética emitida a una frecuencia determinada es proporcional a la cantidad de absorción que experimentaría por la fuente, una propiedad conocida como reciprocidad. Así, una superficie que absorbe más luz roja irradia térmicamente más luz roja. Este principio se aplica a todas las propiedades de la onda, incluyendo longitud de onda (color), dirección, polarización e incluso coherencia, de modo que es posible tener radiación térmica que es polarizada, coherente y direccional, aunque formas polarizadas y coherentes son bastante raras en la naturaleza lejos de las fuentes (en términos de longitud de onda). Véase la sección siguiente para más información sobre esta calificación.
En cuanto a las estadísticas de fotones, la luz térmica obedece a las estadísticas superpoissonianas.
Campo cercano y campo lejano
Las propiedades generales de la radiación térmica descritas por la ley de Planck se aplican si la dimensión lineal de todas las partes consideradas, así como los radios de curvatura de todas las superficies, son grandes en comparación con la longitud de onda del rayo considerado. (típicamente de 8 a 25 micrómetros para el emisor a 300 K). De hecho, la radiación térmica, como se discutió anteriormente, solo tiene en cuenta las ondas radiantes (radiación de campo lejano o electromagnética). Se debe utilizar un marco más sofisticado que involucre la teoría electromagnética para distancias más pequeñas desde la fuente térmica o la superficie (transferencia de calor por radiación de campo cercano). Por ejemplo, aunque la radiación térmica de campo lejano a distancias de superficies de más de una longitud de onda generalmente no es coherente en ningún grado, la radiación térmica de campo cercano (es decir, la radiación a distancias de una fracción de varias longitudes de onda de radiación) puede exhibir un grado de coherencia temporal y espacial.
La ley de radiación térmica de Planck ha sido cuestionada en las últimas décadas por predicciones y demostraciones exitosas de la transferencia de calor por radiación entre objetos separados por brechas a nanoescala que se desvían significativamente de las predicciones de la ley. Esta desviación es especialmente fuerte (hasta varios órdenes de magnitud) cuando el emisor y el absorbente soportan modos de polaritón superficiales que pueden acoplarse a través del espacio que separa los objetos fríos y calientes. Sin embargo, para aprovechar la transferencia de calor radiativo de campo cercano mediada por polaritones superficiales, los dos objetos deben estar separados por espacios ultraestrechos del orden de micras o incluso nanómetros. Esta limitación complica significativamente los diseños de dispositivos prácticos.
Otra forma de modificar el espectro de emisión térmica del objeto es reducir la dimensionalidad del propio emisor. Este enfoque se basa en el concepto de confinamiento de electrones en pozos cuánticos, cables y puntos, y adapta la emisión térmica mediante la ingeniería de estados de fotones confinados en trampas de potencial bidimensionales y tridimensionales, incluidos pozos, cables y puntos. Tal confinamiento espacial concentra estados de fotones y mejora la emisión térmica en frecuencias seleccionadas. Para lograr el nivel requerido de confinamiento de fotones, las dimensiones de los objetos radiantes deben estar en el orden o por debajo de la longitud de onda térmica predicha por la ley de Planck. Lo que es más importante, el espectro de emisión de pozos, cables y puntos térmicos se desvía de las predicciones de la ley de Planck no solo en el campo cercano, sino también en el campo lejano, lo que amplía significativamente el rango de sus aplicaciones.
Color subjetivo al ojo de un radiador térmico de cuerpo negro
| °C (°F) | Color subjetivo |
|---|---|
| 480 °C (896 °F) | débil brillo rojo |
| 580 °C (1,076 °F) | rojo oscuro |
| 730 °C (1,350 °F) | rojo brillante, ligeramente naranja |
| 930 °C (1,710 °F) | naranja brillante |
| 1,100 °C (2,010 °F) | amarillo pálido naranja |
| 1,300 °C (2,370 °F) | blanco amarillento |
| ± 1,400 °C (2,550 °F) | blanco (amarillo si se ve desde una distancia a través de la atmósfera) |
Flujos de calor radiante seleccionados
El tiempo de un daño por exposición al calor radiativo es una función de la tasa de entrega del calor. Flujo de calor radiativo y efectos: (1 W/cm2 = 10 kW/m2)
| kW/m2 | Efecto |
|---|---|
| 170 | Flujo máximo medido en un compartimiento posterior al enfrentamiento |
| 80 | Protector térmico Prueba de rendimiento para equipo de protección personal |
| 52 | Fiberboard ignúa a 5 segundos |
| 29 | Los linajes de madera, dado tiempo |
| 20 | Comienzo típico de la relámpago a nivel de suelo de una habitación residencial |
| 16 | Piel humana: dolor repentino y ampollas de quemadura de segundo grado después de 5 segundos |
| 12,5 | La madera produce volatiles ignibles por pirolisis |
| 10.4 | Piel humana: Dolor después de 3 segundos, ampollas de quemadura de segundo grado después de 9 segundos |
| 6.4 | Piel humana: ampollas de quemadura de segundo grado después de 18 segundos |
| 4.5 | Piel humana: ampollas de quemadura de segundo grado después de 30 segundos |
| 2.5 | Piel humana: quemaduras después de la exposición prolongada, exposición al flujo radiante típicamente encontrada durante la lucha contra incendios |
| 1.4 | Luz solar, quemaduras de sol potencialmente en 30 minutos. Sunburn NO es una quemadura térmica. Es causada por daño celular debido a la radiación ultravioleta. |
Intercambio de energía
La radiación térmica es uno de los tres mecanismos principales de transferencia de calor. Conlleva la emisión de un espectro de radiación electromagnética debido a la temperatura de un objeto. Otros mecanismos son la convección y la conducción.
La transferencia de calor por radiación se diferencia de las otras dos en que no requiere un medio y, de hecho, alcanza la máxima eficiencia en el vacío. La radiación electromagnética tiene algunas características propias dependiendo de la frecuencia y longitudes de onda de la radiación. El fenómeno de la radiación aún no se comprende completamente. Se han utilizado dos teorías para explicar la radiación; sin embargo, ninguno de ellos es perfectamente satisfactorio.
Primero, la teoría anterior que se originó a partir del concepto de un medio hipotético denominado éter. Ether supuestamente llena todos los espacios evacuados o no evacuados. La transmisión de luz o de calor radiante son permitidas por la propagación de ondas electromagnéticas en el éter. Las ondas de transmisión de televisión y radio son tipos de ondas electromagnéticas con longitudes de onda específicas. Todas las ondas electromagnéticas viajan a la misma velocidad; por lo tanto, las longitudes de onda más cortas se asocian con frecuencias altas. Dado que todo cuerpo o fluido está sumergido en el éter, debido a la vibración de las moléculas, cualquier cuerpo o fluido puede potencialmente iniciar una onda electromagnética. Todos los cuerpos generan y reciben ondas electromagnéticas a expensas de su energía almacenada.
La segunda teoría de la radiación es mejor conocida como la teoría cuántica y fue propuesta por primera vez por Max Planck en 1900. Según esta teoría, la energía emitida por un radiador no es continua, sino en forma de cuantos. Planck afirmó que las cantidades tenían diferentes tamaños y frecuencias de vibración de manera similar a la teoría ondulatoria. La energía E se encuentra mediante la expresión E = hν, donde h es la constante de Planck y ν es la frecuencia. Las frecuencias más altas se originan por las altas temperaturas y crean un aumento de energía en el cuanto. Mientras que la propagación de las ondas electromagnéticas de todas las longitudes de onda a menudo se denomina "radiación", la radiación térmica suele limitarse a las regiones visible e infrarroja. Para fines de ingeniería, se puede afirmar que la radiación térmica es una forma de radiación electromagnética que varía según la naturaleza de una superficie y su temperatura. Las ondas de radiación pueden viajar en patrones inusuales en comparación con el flujo de calor por conducción. La radiación permite que las ondas viajen desde un cuerpo caliente a través de un medio frío no absorbente o parcialmente absorbente y lleguen nuevamente a un cuerpo más caliente. Este es el caso de las ondas de radiación que viajan del sol a la tierra.
La interacción del intercambio de energía por radiación térmica se caracteriza por la siguiente ecuación:
- α α +*** *** +τ τ =1.{displaystyle alpha +rho +tau =1.,}
Aquí, α α {displaystyle alpha ,} representa el componente de absorción espectral, *** *** {displaystyle rho ,} componente espectral de reflexión τ τ {displaystyle tau ,} el componente de transmisión espectral. Estos elementos son una función de la longitud de onda (λ λ {displaystyle lambda ,}) de la radiación electromagnética. La absorción espectral es igual a la emisividad ε ε {displaystyle epsilon }; esta relación se conoce como la ley de Kirchhoff de la radiación térmica. Un objeto se llama cuerpo negro si esto sostiene para todas las frecuencias, y la siguiente fórmula se aplica:
- α α =ε ε =1.{displaystyle alpha =epsilon =1.,}
La reflectividad se desvía de las otras propiedades en que es de naturaleza bidireccional. En otras palabras, esta propiedad depende de la dirección del incidente de la radiación así como de la dirección de la reflexión. Por lo tanto, los rayos reflejados de un espectro de radiación que inciden sobre una superficie real en una dirección específica forman una forma irregular que no es fácilmente predecible. En la práctica, a menudo se supone que las superficies se reflejan de manera perfectamente especular o difusa. En una reflexión especular, los ángulos de reflexión e incidencia son iguales. En la reflexión difusa, la radiación se refleja por igual en todas las direcciones. Se puede suponer que la reflexión de superficies lisas y pulidas es una reflexión especular, mientras que la reflexión de superficies rugosas se aproxima a la reflexión difusa. En el análisis de radiación, una superficie se define como lisa si la altura de la rugosidad de la superficie es mucho menor en relación con la longitud de onda de la radiación incidente.
En una situación práctica y a temperatura ambiente, los seres humanos pierden una cantidad considerable de energía debido a la radiación térmica en el infrarrojo, además de la pérdida por conducción al aire (con la ayuda de la convección simultánea u otro movimiento del aire, como corrientes de aire). La energía térmica perdida se recupera parcialmente absorbiendo la radiación térmica de las paredes u otros alrededores. (El calor obtenido por conducción ocurriría para una temperatura del aire más alta que la temperatura corporal). De lo contrario, la temperatura corporal se mantiene a partir del calor generado a través del metabolismo interno. La piel humana tiene una emisividad muy cercana a 1,0. El uso de las fórmulas a continuación muestra que un ser humano, que tiene aproximadamente 2 metros cuadrados de superficie y una temperatura de aproximadamente 307 K, irradia continuamente aproximadamente 1000 vatios. Si las personas están en el interior, rodeadas de superficies a 296 K, reciben unos 900 vatios de la pared, el techo y otros alrededores, por lo que la pérdida neta es de solo unos 100 vatios. Estas estimaciones de transferencia de calor dependen en gran medida de variables extrínsecas, como el uso de ropa, es decir, la disminución de la conductividad térmica total del circuito y, por lo tanto, la reducción del flujo de calor de salida total. Solo los sistemas verdaderamente grises (emisividad/absorción equivalente relativa y sin dependencia de la transmisividad direccional en todos los cuerpos de volumen de control considerados) pueden lograr estimaciones razonables de flujo de calor en estado estacionario a través de Stefan-Boltzmann ley. Al encontrar este "idealmente calculable" La situación es casi imposible (aunque los procedimientos de ingeniería comunes renuncian a la dependencia de estas variables desconocidas y "suponen" que este es el caso). Con optimismo, estos "grises" las aproximaciones se acercarán a las soluciones reales, ya que la mayoría de las divergencias de las soluciones de Stefan-Boltzmann son muy pequeñas (especialmente en la mayoría de los entornos controlados por laboratorio de STP).
Si los objetos aparecen blancos (reflectantes en el espectro visual), no necesariamente son igualmente reflectantes (y, por lo tanto, no emisivos) en el infrarrojo térmico; consulte el diagrama de la izquierda. La mayoría de los radiadores domésticos están pintados de blanco, lo cual es sensato dado que no están lo suficientemente calientes como para irradiar una cantidad significativa de calor, y no están diseñados como radiadores térmicos en absoluto; en cambio, en realidad son convectores, y pintarlos de negro mate haría poco. diferencia en su eficacia. Las pinturas blancas a base de acrílico y uretano tienen una eficiencia de radiación de cuerpo negro del 93 % a temperatura ambiente (lo que significa que el término "cuerpo negro" no siempre se corresponde con el color percibido visualmente de un objeto). Estos materiales que no siguen el "color negro = alta emisividad/absorción" Lo más probable es que la advertencia tenga una dependencia funcional de la emisividad/absorción espectral.
Cálculo de la transferencia de calor por radiación entre grupos de objetos, incluida una 'cavidad' o 'alrededor' requiere la solución de un conjunto de ecuaciones simultáneas utilizando el método de radiosidad. En estos cálculos, la configuración geométrica del problema se destila en un conjunto de números llamados factores de vista, que dan la proporción de radiación que sale de una superficie dada que incide en otra superficie específica. Estos cálculos son importantes en los campos de la energía solar térmica, el diseño de calderas y hornos y los gráficos por computadora con trazado de rayos.
Se puede utilizar una superficie selectiva cuando se extrae energía del sol. Las superficies selectivas también se pueden utilizar en colectores solares. Podemos averiguar qué tan útil es un recubrimiento de superficie selectivo observando la temperatura de equilibrio de una placa que se calienta a través de la radiación solar. Si la placa está recibiendo una irradiación solar de 1350 W/m2 (mínimo 1325 W/m2 el 4 de julio y máximo 1418 W/m2 el 3 de enero) desde el sol, la temperatura de la placa donde la radiación que sale es igual a la radiación que recibe la placa es de 393 K (248 °F). Si la placa tiene una superficie selectiva con una emisividad de 0,9 y una longitud de onda de corte de 2,0 μm, la temperatura de equilibrio es de aproximadamente 1250 K (1790 °F). Los cálculos se realizaron despreciando la transferencia de calor por convección y despreciando la radiación solar absorbida en las nubes/atmósfera por simplicidad, la teoría sigue siendo la misma para un problema real.
Para reducir la transferencia de calor de una superficie, como una ventana de vidrio, se puede colocar una película reflectante transparente con un revestimiento de baja emisividad en el interior de la superficie. "Los recubrimientos de baja emisión (low-E) son capas de metal u óxido metálico microscópicamente delgadas, virtualmente invisibles, depositadas en una ventana o superficie vidriada de un tragaluz principalmente para reducir el factor U al suprimir el flujo de calor radiativo". Al agregar este recubrimiento, estamos limitando la cantidad de radiación que sale de la ventana, aumentando así la cantidad de calor que se retiene dentro de la ventana.
Dado que cualquier radiación electromagnética, incluida la radiación térmica, transmite impulso además de energía, la radiación térmica también induce fuerzas muy pequeñas en los objetos que irradian o absorben. Normalmente, estas fuerzas son insignificantes, pero deben tenerse en cuenta al considerar la navegación de una nave espacial. La anomalía Pioneer, en la que el movimiento de la nave se desvió ligeramente de lo esperado solo por la gravedad, finalmente se atribuyó a la radiación térmica asimétrica de la nave espacial. De manera similar, las órbitas de los asteroides se ven perturbadas ya que el asteroide absorbe la radiación solar en el lado que mira hacia el sol, pero luego vuelve a emitir la energía en un ángulo diferente a medida que la rotación del asteroide saca la superficie cálida del sol. vista (el efecto YORP).
Potencia radiativa
Potencia de radiación térmica de un cuerpo negro en la dirección ortogonal por área unidad de superficie radiante por unidad de ángulo sólido y frecuencia por unidad .. {displaystyle nu } es dada por la ley de Planck como:
- u().. ,T)=2h.. 3c2⋅ ⋅ 1eh.. /kBT− − 1{displaystyle u(nuT)={frac {2hnu ¿Qué? {fnMicroc {1}{e^{hnu /k_{rm {B}T}-1}}
o en lugar de por unidad de frecuencia, por unidad de longitud de onda como
- u()λ λ ,T)=2hc2λ λ 5⋅ ⋅ 1ehc/kBTλ λ − − 1{displaystyle u(lambdaT)={frac {2hc^{2}{lambda ^{5}}}cdot {frac {1}{e^{hc/k_{rm} {B}Tlambda }
Esta fórmula sigue matemáticamente del cálculo de la distribución espectral de la energía en el campo electromagnético cuantificado que está en equilibrio térmico completo con el objeto radiante. La ley Plancks muestra que la energía radiativa aumenta con la temperatura, y explica por qué el pico de un espectro de emisiones cambia a longitudes de onda más cortas a temperaturas más altas. También se puede encontrar que la energía emitida a longitudes de onda más cortas aumenta más rápidamente con temperatura relativa a longitudes de onda más largas. La ecuación se deriva como una suma infinita sobre todas las frecuencias posibles en una región semiesférica. La energía, E=h.. {displaystyle E=hnu }, de cada foton se multiplica por el número de estados disponibles en esa frecuencia, y la probabilidad de que cada uno de esos estados será ocupado.
Integrar la ecuación anterior sobre .. {displaystyle nu } se obtiene la potencia dada por la ley Stefan-Boltzmann, como:
- P=σ σ AT4{displaystyle P=sigma AT^{4}
donde la constante de proporcionalidad σ σ {displaystyle sigma } es la constante Stefan-Boltzmann y A{displaystyle A} es la superficie radiante.
La longitud de onda λ λ {displaystyle lambda ,}, por lo que la intensidad de emisión es mayor, es dada por la ley de desplazamiento de Wien como:
- λ λ max=bT{displaystyle lambda _{max}={frac {B} {T}}
Para superficies que no son cuerpos negros, hay que considerar el factor de emisividad (generalmente dependiente de frecuencia) ε ε ().. ){displaystyle epsilon (nu)}. Este factor debe multiplicarse con la fórmula del espectro de radiación antes de la integración. Si se toma como una constante, la fórmula resultante para la salida de potencia se puede escribir de una manera que contenga ε ε {displaystyle epsilon } como factor:
- P=ε ε σ σ AT4{displaystyle P=epsilon sigma AT^{4}
Este tipo de modelo teórico, con una emisividad independiente de la frecuencia inferior a la de un cuerpo negro perfecto, se conoce a menudo como cuerpo gris. Para la emisividad dependiente de la frecuencia, la solución para la potencia integrada depende de la forma funcional de la dependencia, aunque en general no existe una expresión simple para ello. En términos prácticos, si la emisividad del cuerpo es aproximadamente constante alrededor de la longitud de onda de emisión máxima, el modelo de cuerpo gris tiende a funcionar bastante bien, ya que el peso de la curva alrededor de la emisión máxima tiende a dominar la integral.
Constantes
Definiciones de constantes utilizadas en las ecuaciones anteriores:
| h{displaystyle h,} | Planck constante | 6.626 069 3(11)×10−34− J·s = 4.135 667 43(35)×10−15 eV·s |
| b{displaystyle b,} | El desplazamiento constante de Wien | 2.897 768 5(51)×10−3 m·K |
| kB{displaystyle k_{rm {B},} | Pertzmann constante | 1.380 650 5(24)×10,23 a 23 J·K−1 = 8.617 343 (15)×10; 5 - eV·K−1 |
| σ σ {displaystyle sigma ,} | Stefan-Boltzmann constante | 5.670 373 (21)×10−8 W·m−2·K−4 |
| c{displaystyle c,} | Velocidad de luz | 299 792 458 m·s−1 |
Variables
Definiciones de variables, con valores de ejemplo:
| T{displaystyle T} | Temperatura absoluta | Para unidades utilizadas anteriormente, debe estar en kelvins (por ejemplo, temperatura media de la superficie en la Tierra = 288 K) |
| A{displaystyle A} | Superficie | Acuboide = 2ab + 2bc + 2ac; Acilindro = 2π·r()h + r); Aesfera = 4π·r2 |
Transferencia de calor por radiación
La transferencia de calor por radiación neta de una superficie a otra es la radiación que sale de la primera superficie hacia la otra menos la que llega de la segunda superficie.
- Para los cuerpos negros, la tasa de transferencia de energía de la superficie 1 a la superficie 2 es:
- QÍ Í 1→ → 2=A1Eb1F1→ → 2− − A2Eb2F2→ → 1{displaystyle { dot {Q}_{1derecho 2}=A_{1}E_{b1}F_{1rightarrow 2}-A_{2}E_{b2}F_{2rightarrow 1}
Donde A{displaystyle A} es superficie, Eb{displaystyle E_{b} es flujo de energía (la tasa de emisión por superficie unidad) y F1→ → 2{displaystyle F_{1derecho 2}} es el factor de vista de la superficie 1 a la superficie 2. Aplicando tanto la regla de reciprocidad para los factores de vista, A1F1→ → 2=A2F2→ → 1{displaystyle A_{1}F_{1rightarrow 2}=A_{2}F_{2rightarrow 1}, y la ley Stefan-Boltzmann, Eb=σ σ T4{displaystyle E_{b}=sigma T^{4}, rendimientos:
- QÍ Í 1→ → 2=σ σ A1F1→ → 2()T14− − T24){displaystyle { dot {}_{1rightarrow 2}=sigma A_{1}F_{1rightarrow 2}left ¡Oh!
- Para dos superficies de cuerpo gris formando un recinto, la tasa de transferencia de calor es:
- QÍ Í =σ σ ()T14− − T24)1− − ε ε 1A1ε ε 1+1A1F1→ → 2+1− − ε ε 2A2ε ε 2{displaystyle { dot {}={sigmaleft (T_{1} {4}-T_{2}right)}{displaystyle {frac {1-epsilon ## {1}{1}epsilon ¿Qué? {1}{1}F_{1}derecho 2}}+{frac {1-epsilon ## {2}{2}epsilon ♪♪
Las fórmulas para la transferencia de calor por radiación se pueden derivar para arreglos físicos más particulares o más elaborados, como entre placas paralelas, esferas concéntricas y las superficies internas de un cilindro.
Contenido relacionado
Hideki Yukawa
Lee Smolin
Dyson