Radiación electromagnética
En física, la radiación electromagnética (EMR) consiste en ondas del campo electromagnético (EM), que se propagan a través del espacio y transportan impulso y energía electromagnética radiante. Incluye ondas de radio, microondas, infrarrojos, luz (visible), ultravioleta, rayos X y rayos gamma. Todas estas ondas forman parte del espectro electromagnético.
Clásicamente, la radiación electromagnética consiste en ondas electromagnéticas, que son oscilaciones sincronizadas de campos eléctricos y magnéticos. Dependiendo de la frecuencia de oscilación, se producen diferentes longitudes de onda del espectro electromagnético. En el vacío, las ondas electromagnéticas viajan a la velocidad de la luz, comúnmente denominadas c. En medios isotrópicos homogéneos, las oscilaciones de los dos campos son perpendiculares entre sí y perpendiculares a la dirección de propagación de la energía y la onda, formando una onda transversal. La posición de una onda electromagnética dentro del espectro electromagnético se puede caracterizar por su frecuencia de oscilación o por su longitud de onda. Las ondas electromagnéticas de diferente frecuencia reciben diferentes nombres ya que tienen diferentes fuentes y efectos sobre la materia. En orden de frecuencia creciente y longitud de onda decreciente, estos son: ondas de radio, microondas, radiación infrarroja, luz visible, radiación ultravioleta, rayos X y rayos gamma.
Las ondas electromagnéticas son emitidas por partículas cargadas eléctricamente que se aceleran, y estas ondas pueden interactuar posteriormente con otras partículas cargadas, ejerciendo fuerza sobre ellas. Las ondas EM transportan energía, momento y momento angular lejos de su partícula fuente y pueden impartir esas cantidades a la materia con la que interactúan. La radiación electromagnética está asociada con aquellas ondas EM que son libres de propagarse ("irradiar") sin la influencia continua de las cargas en movimiento que las produjeron, porque han alcanzado una distancia suficiente de esas cargas. Por lo tanto, EMR a veces se denomina campo lejano. En este lenguaje, el campo cercano se refiere a los campos EM cerca de las cargas y corrientes que los produjeron directamente, específicamente los fenómenos de inducción electromagnética e inducción electrostática.
En la mecánica cuántica, una forma alternativa de ver la EMR es que consta de fotones, partículas elementales sin carga con masa en reposo cero que son los cuantos del campo electromagnético, responsables de todas las interacciones electromagnéticas. La electrodinámica cuántica es la teoría de cómo la EMR interactúa con la materia a nivel atómico. Los efectos cuánticos proporcionan fuentes adicionales de EMR, como la transición de electrones a niveles de energía más bajos en un átomo y la radiación de cuerpo negro. La energía de un fotón individual está cuantificada y es mayor para fotones de mayor frecuencia. Esta relación viene dada por la ecuación de Planck E = hf, donde E es la energía por fotón, f es la frecuencia del fotón y h es la constante de Planck. Un solo fotón de rayos gamma, por ejemplo, podría transportar unas 100 000 veces la energía de un solo fotón de luz visible.
Los efectos de la EMR sobre los compuestos químicos y los organismos biológicos dependen tanto de la potencia de la radiación como de su frecuencia. La EMR de frecuencias visibles o más bajas (es decir, luz visible, infrarrojos, microondas y ondas de radio) se denomina radiación no ionizante, porque sus fotones individualmente no tienen suficiente energía para ionizar átomos o moléculas, o romper enlaces químicos. Los efectos de estas radiaciones en los sistemas químicos y los tejidos vivos se deben principalmente a los efectos de calentamiento de la transferencia de energía combinada de muchos fotones. Por el contrario, los rayos ultravioleta de alta frecuencia, los rayos X y los rayos gamma se denominan radiación ionizante, ya que los fotones individuales de tan alta frecuencia tienen suficiente energía para ionizar moléculas o romper enlaces químicos. Estas radiaciones tienen la capacidad de causar reacciones químicas y dañar las células vivas más allá de lo que resulta del simple calentamiento, y pueden ser un peligro para la salud.
Física
Teoría
Ecuaciones de Maxwell
James Clerk Maxwell derivó una forma de onda de las ecuaciones eléctricas y magnéticas, descubriendo así la naturaleza ondulatoria de los campos eléctricos y magnéticos y su simetría. Debido a que la velocidad de las ondas EM predicha por la ecuación de onda coincidió con la velocidad medida de la luz, Maxwell concluyó que la luz en sí misma es una onda EM. Las ecuaciones de Maxwell fueron confirmadas por Heinrich Hertz a través de experimentos con ondas de radio.
Maxwell se dio cuenta de que, dado que gran parte de la física es simétrica y matemáticamente artística en cierto modo, también debe haber una simetría entre la electricidad y el magnetismo. Se dio cuenta de que la luz es una combinación de electricidad y magnetismo y, por lo tanto, los dos deben estar unidos. De acuerdo con las ecuaciones de Maxwell, un campo eléctrico que varía espacialmente siempre está asociado con un campo magnético que cambia con el tiempo. Asimismo, un campo magnético que varía espacialmente está asociado con cambios específicos en el tiempo en el campo eléctrico. En una onda electromagnética, los cambios en el campo eléctrico siempre van acompañados de una onda en el campo magnético en una dirección, y viceversa. Esta relación entre los dos ocurre sin que ningún tipo de campo cause al otro; más bien, ocurren juntos de la misma manera que los cambios de tiempo y espacio ocurren juntos y están interrelacionados en la relatividad especial. De hecho, los campos magnéticos pueden verse como campos eléctricos en otro marco de referencia, y los campos eléctricos pueden verse como campos magnéticos en otro marco de referencia, pero tienen el mismo significado ya que la física es la misma en todos los marcos de referencia, por lo que la La estrecha relación entre los cambios de espacio y tiempo aquí es más que una analogía. Juntos, estos campos forman una onda electromagnética que se propaga, que se mueve hacia el espacio y nunca más necesita interactuar con la fuente. El campo EM distante formado de esta manera por la aceleración de una carga transporta energía que "irradia" lejos a través del espacio, de ahí el término.
Campos cercanos y lejanos

Las ecuaciones de Maxwell establecieron que algunas cargas y corrientes ("fuentes") producen un tipo local de campo electromagnético cerca de ellas que no tiene el comportamiento de EMR. Las corrientes producen directamente un campo magnético, pero es de tipo dipolo magnético que se extingue con la distancia de la corriente. De manera similar, las cargas en movimiento separadas en un conductor por un potencial eléctrico cambiante (como en una antena) producen un campo eléctrico de tipo dipolo eléctrico, pero esto también disminuye con la distancia. Estos campos forman el campo cercano cerca de la fuente EMR. Ninguno de estos comportamientos es responsable de la radiación EM. En cambio, provocan un comportamiento de campo electromagnético que solo transfiere energía de manera eficiente a un receptor muy cercano a la fuente, como la inducción magnética dentro de un transformador o el comportamiento de retroalimentación que ocurre cerca de la bobina de un detector de metales. Por lo general, los campos cercanos tienen un efecto poderoso en sus propias fuentes, lo que provoca un aumento de la "carga" (reactancia eléctrica disminuida) en la fuente o transmisor, siempre que un receptor extraiga energía del campo EM. De lo contrario, estos campos no se "propagan" libremente al espacio, llevándose su energía sin límite de distancia, sino que oscilan, devolviendo su energía al transmisor si no es recibida por un receptor.
Por el contrario, el campo lejano EM se compone de radiación que está libre del transmisor en el sentido de que (a diferencia del caso de un transformador eléctrico) el transmisor requiere la misma potencia para enviar estos cambios en los campos, ya sea que la señal se capte inmediatamente o no. Esta parte distante del campo electromagnético es "radiación electromagnética" (también llamado campo lejano). Los campos lejanos se propagan (irradian) sin permitir que el transmisor los afecte. Esto hace que sean independientes en el sentido de que su existencia y su energía, después de haber dejado el transmisor, es completamente independiente tanto del transmisor como del receptor. Debido a la conservación de la energía, la cantidad de energía que pasa a través de cualquier superficie esférica alrededor de la fuente es la misma. Debido a que dicha superficie tiene un área proporcional al cuadrado de su distancia desde la fuente, la densidad de potencia de la radiación EM siempre disminuye con el inverso del cuadrado de la distancia desde la fuente; esto se llama la ley del cuadrado inverso. Esto contrasta con las partes dipolares del campo EM cerca de la fuente (el campo cercano), que varían en potencia de acuerdo con una ley de potencia del cubo inverso y, por lo tanto, no transportan una cantidad conservada de energía a través de las distancias, sino que se desvanece con la distancia, y su energía (como se indica) regresa rápidamente al transmisor o es absorbida por un receptor cercano (como la bobina secundaria de un transformador).
El campo lejano (EMR) depende de un mecanismo diferente para su producción que el campo cercano y de diferentes términos en las ecuaciones de Maxwell. Mientras que la parte magnética del campo cercano se debe a las corrientes en la fuente, el campo magnético en EMR se debe solo al cambio local en el campo eléctrico. De manera similar, mientras que el campo eléctrico en el campo cercano se debe directamente a las cargas y la separación de carga en la fuente, el campo eléctrico en EMR se debe a un cambio en el campo magnético local. Ambos procesos para producir campos EMR eléctricos y magnéticos tienen una dependencia diferente de la distancia que los campos magnéticos y eléctricos dipolares de campo cercano. Es por eso que el tipo de campo EM EMR se vuelve dominante en el poder 'lejos'. de fuentes El término "lejos de las fuentes" se refiere a qué tan lejos de la fuente (moviéndose a la velocidad de la luz) se encuentra cualquier parte del campo EM que se mueve hacia afuera, en el momento en que las corrientes de la fuente cambian por el potencial variable de la fuente y, por lo tanto, la fuente ha comenzado a generar un campo EM que se mueve hacia afuera de una fase diferente.
Una visión más compacta de EMR es que el campo lejano que compone EMR es generalmente la parte del campo EM que ha viajado una distancia suficiente desde la fuente, que se ha desconectado por completo de cualquier retroalimentación a las cargas y corrientes que fueron originalmente responsables de ello. Ahora, independientemente de las cargas de origen, el campo EM, a medida que se aleja, depende solo de las aceleraciones de las cargas que lo produjeron. Ya no tiene una fuerte conexión con los campos directos de las cargas, o con la velocidad de las cargas (corrientes).
En la formulación potencial de Liénard-Wiechert de los campos eléctrico y magnético debido al movimiento de una sola partícula (según las ecuaciones de Maxwell), los términos asociados con la aceleración de la partícula son los que son responsables de la parte del campo que se considera radiación electromagnética. Por el contrario, el término asociado con el campo eléctrico estático cambiante de la partícula y el término magnético que resulta de la velocidad uniforme de la partícula están asociados con el campo cercano electromagnético y no comprenden la radiación EM.
Propiedades

La electrodinámica es la física de la radiación electromagnética, y el electromagnetismo es el fenómeno físico asociado con la teoría de la electrodinámica. Los campos eléctrico y magnético obedecen a las propiedades de superposición. Así, un campo debido a cualquier partícula en particular o campo eléctrico o magnético variable en el tiempo contribuye a los campos presentes en el mismo espacio debido a otras causas. Además, como son campos vectoriales, todos los vectores de campo magnético y eléctrico se suman según la suma de vectores. Por ejemplo, en óptica, dos o más ondas de luz coherentes pueden interactuar y, por interferencia constructiva o destructiva, producir una irradiancia resultante que se desvía de la suma de las irradiaciones componentes de las ondas de luz individuales.
Los campos electromagnéticos de la luz no se ven afectados al viajar a través de campos magnéticos o eléctricos estáticos en un medio lineal como el vacío. Sin embargo, en medios no lineales, como algunos cristales, pueden ocurrir interacciones entre la luz y los campos eléctricos y magnéticos estáticos; estas interacciones incluyen el efecto Faraday y el efecto Kerr.
En la refracción, una onda que cruza de un medio a otro de distinta densidad altera su velocidad y dirección al entrar en el nuevo medio. La relación de los índices de refracción de los medios determina el grado de refracción y se resume en la ley de Snell. La luz de longitudes de onda compuestas (luz solar natural) se dispersa en un espectro visible que pasa a través de un prisma, debido al índice de refracción dependiente de la longitud de onda del material del prisma (dispersión); es decir, cada onda componente dentro de la luz compuesta se dobla en una cantidad diferente.
La radiación EM exhibe propiedades tanto de onda como de partícula al mismo tiempo (ver dualidad onda-partícula). Tanto las características de las ondas como las de las partículas han sido confirmadas en muchos experimentos. Las características de las ondas son más evidentes cuando la radiación EM se mide en escalas de tiempo relativamente grandes y en grandes distancias, mientras que las características de las partículas son más evidentes cuando se miden escalas de tiempo y distancias pequeñas. Por ejemplo, cuando la radiación electromagnética es absorbida por la materia, las propiedades similares a las partículas serán más obvias cuando el número promedio de fotones en el cubo de la longitud de onda relevante sea mucho menor que 1. No es tan difícil observar experimentalmente la deposición no uniforme. de energía cuando se absorbe la luz, sin embargo, esto por sí solo no es evidencia de "partículas" comportamiento. Más bien, refleja la naturaleza cuántica de la materia. Demostrar que la luz en sí está cuantificada, no solo su interacción con la materia, es un asunto más sutil.
Algunos experimentos muestran la naturaleza ondulatoria y corpuscular de las ondas electromagnéticas, como la autointerferencia de un único fotón. Cuando se envía un solo fotón a través de un interferómetro, pasa a través de ambos caminos, interfiriendo consigo mismo, como lo hacen las ondas, pero es detectado por un fotomultiplicador u otro detector sensible solo una vez.
La teoría de la electrodinámica cuántica describe una teoría cuántica de la interacción entre la radiación electromagnética y la materia, como los electrones.
Las ondas electromagnéticas se pueden polarizar, reflejar, refractar, difractar o interferir entre sí.
Modelo de onda
En medios isotrópicos homogéneos, la radiación electromagnética es una onda transversal, lo que significa que sus oscilaciones son perpendiculares a la dirección de transferencia y viaje de la energía. Proviene de las siguientes ecuaciones:
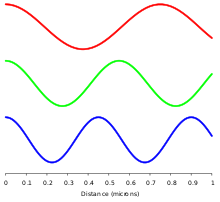
Las partes eléctrica y magnética del campo en una onda electromagnética se mantienen en una proporción fija de fuerzas para satisfacer las dos ecuaciones de Maxwell que especifican cómo se produce una a partir de la otra. En los medios sin disipación (sin pérdidas), estos campos E y B también están en fase, y ambos alcanzan máximos y mínimos en los mismos puntos del espacio (consulte las ilustraciones). Un concepto erróneo común es que los campos E y B en la radiación electromagnética están desfasados porque un cambio en uno produce el otro, y esto produciría una diferencia de fase entre ellos como funciones sinusoidales (como sucede en la inducción electromagnética y en el campo cercano cercano a las antenas). Sin embargo, en la radiación EM de campo lejano que se describe mediante las dos ecuaciones de operador rotacional de Maxwell sin fuente, una descripción más correcta es que un cambio de tiempo en un tipo de campo es proporcional a un cambio de espacio en el otro. Estos derivados requieren que los campos E y B en EMR estén en fase (consulte la sección de matemáticas a continuación). Un aspecto importante de la naturaleza de la luz es su frecuencia. La frecuencia de una onda es su tasa de oscilación y se mide en hercios, la unidad de frecuencia del SI, donde un hercio es igual a una oscilación por segundo. La luz suele tener múltiples frecuencias que se suman para formar la onda resultante. Diferentes frecuencias experimentan diferentes ángulos de refracción, un fenómeno conocido como dispersión.
Una onda monocromática (una onda de una sola frecuencia) consta de valles y crestas sucesivos, y la distancia entre dos crestas o valles adyacentes se denomina longitud de onda. Las ondas del espectro electromagnético varían en tamaño, desde ondas de radio muy largas, más largas que un continente, hasta rayos gamma muy cortos, más pequeños que los núcleos atómicos. La frecuencia es inversamente proporcional a la longitud de onda, según la ecuación:
- v=fλ λ {displaystyle displaystyle v=flambda }
donde v es la velocidad de la onda (c en el vacío o menos en otros medios), f es la frecuencia y λ es la longitud de onda. A medida que las ondas cruzan los límites entre diferentes medios, sus velocidades cambian pero sus frecuencias permanecen constantes.
Las ondas electromagnéticas en el espacio libre deben ser soluciones de la ecuación de ondas electromagnéticas de Maxwell. Se conocen dos clases principales de soluciones, a saber, ondas planas y ondas esféricas. Las ondas planas pueden verse como el caso límite de ondas esféricas a una distancia muy grande (idealmente infinita) de la fuente. Ambos tipos de ondas pueden tener una forma de onda que es una función de tiempo arbitraria (siempre que sea lo suficientemente diferenciable para ajustarse a la ecuación de onda). Como con cualquier función de tiempo, esto se puede descomponer por medio del análisis de Fourier en su espectro de frecuencia, o componentes sinusoidales individuales, cada uno de los cuales contiene una sola frecuencia, amplitud y fase. Se dice que una onda de este tipo es monocromática. Una onda electromagnética monocromática se puede caracterizar por su frecuencia o longitud de onda, su amplitud máxima, su fase relativa a alguna fase de referencia, su dirección de propagación y su polarización.
La interferencia es la superposición de dos o más ondas que dan como resultado un nuevo patrón de ondas. Si los campos tienen componentes en la misma dirección, interfieren constructivamente, mientras que las direcciones opuestas causan interferencia destructiva. Un ejemplo de interferencia causada por EMR es la interferencia electromagnética (EMI) o, como se la conoce más comúnmente, interferencia de radiofrecuencia (RFI). Además, se pueden combinar múltiples señales de polarización (es decir, interferir) para formar nuevos estados de polarización, lo que se conoce como generación de estado de polarización paralela.
La energía de las ondas electromagnéticas a veces se denomina energía radiante.
Modelo de partículas y teoría cuántica
A finales del siglo XIX surgió una anomalía relacionada con una contradicción entre la teoría ondulatoria de la luz y las mediciones de los espectros electromagnéticos que emitían los radiadores térmicos conocidos como cuerpos negros. Los físicos lucharon sin éxito con este problema durante muchos años. Más tarde se conoció como la catástrofe ultravioleta. En 1900, Max Planck desarrolló una nueva teoría de la radiación del cuerpo negro que explicaba el espectro observado. La teoría de Planck se basaba en la idea de que los cuerpos negros emiten luz (y otra radiación electromagnética) solo como haces o paquetes discretos de energía. Estos paquetes fueron llamados cuantos. En 1905, Albert Einstein propuso que los cuantos de luz se consideraran partículas reales. Posteriormente, a la partícula de luz se le dio el nombre de fotón, en correspondencia con otras partículas que se describen en esta época, como el electrón y el protón. Un fotón tiene una energía, E, proporcional a su frecuencia, f, por
- E=hf=hcλ λ {displaystyle E=hf={frac {hc}{lambda },!
Donde h Es constante de Planck, λ λ {displaystyle lambda } es la longitud de onda y c es la velocidad de la luz. Esto se conoce a veces como la ecuación Planck-Einstein. En la teoría cuántica (ver primera cuantificación) la energía de los fotones es por lo tanto directamente proporcional a la frecuencia de la onda EMR.
Del mismo modo, el momento p de un fotón también es proporcional a su frecuencia e inversamente proporcional a su longitud de onda:
- p=Ec=hfc=hλ λ .{displaystyle p={E over c}={hf over c}={h over lambda }
La fuente de la propuesta de Einstein de que la luz estaba compuesta de partículas (o podría actuar como partículas en algunas circunstancias) fue una anomalía experimental no explicada por la teoría ondulatoria: el efecto fotoeléctrico, en el que la luz incide sobre una superficie metálica. electrones expulsados de la superficie, lo que hace que una corriente eléctrica fluya a través de un voltaje aplicado. Las mediciones experimentales demostraron que la energía de los electrones individuales expulsados era proporcional a la frecuencia, en lugar de a la intensidad, de la luz. Además, por debajo de cierta frecuencia mínima, que dependía del metal en particular, no fluiría corriente independientemente de la intensidad. Estas observaciones parecían contradecir la teoría ondulatoria, y durante años los físicos intentaron en vano encontrar una explicación. En 1905, Einstein explicó este enigma resucitando la teoría de partículas de la luz para explicar el efecto observado. Sin embargo, debido a la preponderancia de la evidencia a favor de la teoría ondulatoria, las ideas de Einstein fueron inicialmente recibidas con gran escepticismo entre los físicos establecidos. Finalmente, la explicación de Einstein fue aceptada ya que se observó un nuevo comportamiento de la luz similar a una partícula, como el efecto Compton.
Cuando un átomo absorbe un fotón, lo excita y eleva un electrón a un nivel de energía más alto (uno que, en promedio, está más lejos del núcleo). Cuando un electrón en una molécula o átomo excitado desciende a un nivel de energía más bajo, emite un fotón de luz a una frecuencia correspondiente a la diferencia de energía. Dado que los niveles de energía de los electrones en los átomos son discretos, cada elemento y cada molécula emite y absorbe sus propias frecuencias características. La emisión inmediata de fotones se llama fluorescencia, un tipo de fotoluminiscencia. Un ejemplo es la luz visible emitida por pinturas fluorescentes, en respuesta a la luz ultravioleta (luz negra). Se conocen muchas otras emisiones fluorescentes en bandas espectrales distintas de la luz visible. La emisión retardada se llama fosforescencia.
Dualidad onda-partícula
La teoría moderna que explica la naturaleza de la luz incluye la noción de dualidad onda-partícula. De manera más general, la teoría establece que todo tiene tanto una naturaleza corpuscular como una naturaleza ondulatoria, y se pueden realizar varios experimentos para sacar a relucir una u otra. La naturaleza de la partícula se discierne más fácilmente usando un objeto con una gran masa. Una propuesta audaz de Louis de Broglie en 1924 llevó a la comunidad científica a darse cuenta de que la materia (por ejemplo, los electrones) también presenta una dualidad onda-partícula.
Efectos de ondas y partículas de la radiación electromagnética
Juntos, los efectos de ondas y partículas explican completamente los espectros de emisión y absorción de la radiación EM. La composición de la materia del medio a través del cual viaja la luz determina la naturaleza del espectro de absorción y emisión. Estas bandas corresponden a los niveles de energía permitidos en los átomos. Las bandas oscuras en el espectro de absorción se deben a los átomos en un medio intermedio entre la fuente y el observador. Los átomos absorben ciertas frecuencias de la luz entre el emisor y el detector/ojo, luego las emiten en todas las direcciones. Aparece una banda oscura en el detector, debido a la radiación dispersada por el haz. Por ejemplo, las bandas oscuras en la luz emitida por una estrella distante se deben a los átomos en la atmósfera de la estrella. Un fenómeno similar ocurre con la emisión, que se observa cuando un gas emisor brilla debido a la excitación de los átomos por cualquier mecanismo, incluido el calor. A medida que los electrones descienden a niveles de energía más bajos, se emite un espectro que representa los saltos entre los niveles de energía de los electrones, pero se ven líneas porque nuevamente la emisión ocurre solo a energías particulares después de la excitación. Un ejemplo es el espectro de emisión de las nebulosas. Los electrones que se mueven rápidamente se aceleran más bruscamente cuando encuentran una región de fuerza, por lo que son responsables de producir gran parte de la radiación electromagnética de frecuencia más alta observada en la naturaleza.
Estos fenómenos pueden ayudar a varias determinaciones químicas de la composición de los gases iluminados desde atrás (espectros de absorción) y de los gases incandescentes (espectros de emisión). La espectroscopia (por ejemplo) determina qué elementos químicos componen una estrella en particular. La espectroscopia también se usa en la determinación de la distancia de una estrella, usando el desplazamiento hacia el rojo.
Velocidad de propagación
Cuando cualquier cable (u otro objeto conductor como una antena) conduce corriente alterna, la radiación electromagnética se propaga a la misma frecuencia que la corriente. En muchas de estas situaciones, es posible identificar un momento dipolar eléctrico que surge de la separación de cargas debido al potencial eléctrico excitante, y este momento dipolar oscila en el tiempo, a medida que las cargas se mueven de un lado a otro. Esta oscilación a una frecuencia dada da lugar a campos eléctricos y magnéticos cambiantes, que luego ponen en movimiento la radiación electromagnética.
A nivel cuántico, la radiación electromagnética se produce cuando el paquete de ondas de una partícula cargada oscila o se acelera. Las partículas cargadas en un estado estacionario no se mueven, pero una superposición de tales estados puede resultar en un estado de transición que tiene un momento dipolar eléctrico que oscila en el tiempo. Este momento dipolar oscilante es responsable del fenómeno de transición radiativa entre estados cuánticos de una partícula cargada. Dichos estados ocurren (por ejemplo) en los átomos cuando se irradian fotones cuando el átomo cambia de un estado estacionario a otro.
Como onda, la luz se caracteriza por una velocidad (la velocidad de la luz), una longitud de onda y una frecuencia. Como partículas, la luz es una corriente de fotones. Cada uno tiene una energía relacionada con la frecuencia de la onda dada por la relación de Planck E = hf, donde E es la energía del fotón, h es la constante de Planck, 6,626 × 10−34 J·s, y f es la frecuencia de la onda.
Se obedece una regla independientemente de las circunstancias: la radiación EM en el vacío viaja a la velocidad de la luz, en relación con el observador, independientemente de la velocidad del observador. En un medio (que no sea el vacío), se consideran el factor de velocidad o el índice de refracción, según la frecuencia y la aplicación. Ambos son proporciones de la velocidad en un medio a la velocidad en el vacío.
Teoría especial de la relatividad
A finales del siglo XIX, varias anomalías experimentales no podían explicarse mediante la teoría ondulatoria simple. Una de estas anomalías implicó una controversia sobre la velocidad de la luz. La velocidad de la luz y otros EMR predichos por las ecuaciones de Maxwell no aparecían a menos que las ecuaciones fueran modificadas de una manera sugerida por primera vez por FitzGerald y Lorentz (ver historia de la relatividad especial), o de lo contrario esa velocidad dependería de la velocidad del observador relativo al "medio" (llamado éter luminífero) que supuestamente "llevaba" la onda electromagnética (de manera análoga a la forma en que el aire transporta las ondas sonoras). Los experimentos no lograron encontrar ningún efecto del observador. En 1905, Einstein propuso que el espacio y el tiempo parecían ser entidades de velocidad variable para la propagación de la luz y todos los demás procesos y leyes. Estos cambios explicaron la constancia de la velocidad de la luz y toda la radiación electromagnética, desde el punto de vista de todos los observadores, incluso aquellos en movimiento relativo.
Historia del descubrimiento
La radiación electromagnética de longitudes de onda distintas a las de la luz visible se descubrió a principios del siglo XIX. El descubrimiento de la radiación infrarroja se atribuye al astrónomo William Herschel, quien publicó sus resultados en 1800 ante la Royal Society de Londres. Herschel usó un prisma de vidrio para refractar la luz del Sol y detectó rayos invisibles que causaron un calentamiento más allá de la parte roja del espectro, a través de un aumento en la temperatura registrada con un termómetro. Estos "rayos caloríficos" más tarde se denominaron infrarrojos.
En 1801, el físico alemán Johann Wilhelm Ritter descubrió la luz ultravioleta en un experimento similar al de Herschel, usando luz solar y un prisma de vidrio. Ritter notó que los rayos invisibles cerca del borde violeta de un espectro solar dispersados por un prisma triangular oscurecían las preparaciones de cloruro de plata más rápidamente que la luz violeta cercana. Los experimentos de Ritter fueron un precursor temprano de lo que se convertiría en fotografía. Ritter observó que los rayos ultravioleta (que en un principio se denominaron 'rayos químicos') eran capaces de provocar reacciones químicas.
En 1862–64, James Clerk Maxwell desarrolló ecuaciones para el campo electromagnético que sugerían que las ondas en el campo viajarían a una velocidad muy cercana a la velocidad conocida de la luz. Por lo tanto, Maxwell sugirió que la luz visible (así como los rayos infrarrojos y ultravioleta invisibles por inferencia) consistían en la propagación de perturbaciones (o radiación) en el campo electromagnético. Las ondas de radio fueron producidas deliberadamente por primera vez por Heinrich Hertz en 1887, utilizando circuitos eléctricos calculados para producir oscilaciones a una frecuencia mucho más baja que la de la luz visible, siguiendo recetas para producir cargas y corrientes oscilantes sugeridas por las ecuaciones de Maxwell. Hertz también desarrolló formas de detectar estas ondas y produjo y caracterizó lo que más tarde se denominó ondas de radio y microondas.
Wilhelm Röntgen descubrió y dio nombre a los rayos X. Después de experimentar con altos voltajes aplicados a un tubo de vacío el 8 de noviembre de 1895, notó una fluorescencia en una placa cercana de vidrio revestido. En un mes, descubrió los rayos X' propiedades principales.
La última parte del espectro EM que se descubrió estaba asociada con la radiactividad. Henri Becquerel descubrió que las sales de uranio provocaban el empañamiento de una placa fotográfica no expuesta a través de un papel de cobertura de manera similar a los rayos X, y Marie Curie descubrió que solo ciertos elementos emitían estos rayos de energía, y pronto descubrió la intensa radiación del radio. La radiación de la pechblenda fue diferenciada en rayos alfa (partículas alfa) y rayos beta (partículas beta) por Ernest Rutherford a través de experimentos simples en 1899, pero estos resultaron ser tipos de radiación de partículas cargadas. Sin embargo, en 1900 el científico francés Paul Villard descubrió un tercer tipo de radiación del radio con carga neutra y especialmente penetrante, y después de que lo describió, Rutherford se dio cuenta de que debía ser un tercer tipo de radiación, que en 1903 Rutherford denominó rayos gamma. En 1910, el físico británico William Henry Bragg demostró que los rayos gamma son radiación electromagnética, no partículas, y en 1914 Rutherford y Edward Andrade midieron sus longitudes de onda y descubrieron que eran similares a los rayos X pero con longitudes de onda más cortas y frecuencias más altas, aunque un &# 39;cruce' entre los rayos X y gamma hace posible tener rayos X con una energía más alta (y por lo tanto una longitud de onda más corta) que los rayos gamma y viceversa. El origen del rayo los diferencia, los rayos gamma tienden a ser fenómenos naturales que se originan en el núcleo inestable de un átomo y los rayos X son generados eléctricamente (y por lo tanto hechos por el hombre) a menos que sean como resultado de la radiación X de bremsstrahlung causada por la interacción de partículas que se mueven rápidamente (como las partículas beta) que chocan con ciertos materiales, generalmente de números atómicos más altos.
Espectro electromagnético

γ = rayos gamma
HX = radiografías duras
SX = Rayos X blandos
EUV = Extreme-ultraviolet
NUV = Cercano-ultravioleta
Luz visible (bandas coloreadas)
NIR = infrarrojos cercanos
MIR = Mid-infrared
FIR = Far-infrared
EHF = Frecuencia extremadamente alta (microwaves)
SHF = Super-alta frecuencia (microwaves)
UHF = Frecuencia ultraalta (olas de radio)
VHF = Muy alta frecuencia (radio)
HF = Alta frecuencia (radio)
MF = Frecuencia media (radio)
LF = Baja frecuencia (radio)
VLF = Muy baja frecuencia (radio)
VF = frecuencia de voz
ULF = Frecuencia ultra-bajo (radio)
SLF = Frecuencia super-bajo (radio)
ELF = Muy baja frecuencia (radio)
La radiación EM (la designación 'radiación' excluye la electricidad estática y los campos magnéticos y cercanos) se clasifica por longitud de onda en radio, microondas, infrarrojos, visible, ultravioleta, rayos X y rayos gamma. Las ondas electromagnéticas arbitrarias se pueden expresar mediante el análisis de Fourier en términos de ondas monocromáticas sinusoidales, que a su vez se pueden clasificar en estas regiones del espectro EMR.
Para ciertas clases de ondas EM, la forma de onda se trata de manera más útil como aleatoria, y luego el análisis espectral debe realizarse mediante técnicas matemáticas ligeramente diferentes apropiadas para procesos aleatorios o estocásticos. En tales casos, los componentes de frecuencia individuales se representan en términos de su contenido de potencia y la información de fase no se conserva. Tal representación se denomina densidad espectral de potencia del proceso aleatorio. La radiación electromagnética aleatoria que requiere este tipo de análisis se encuentra, por ejemplo, en el interior de las estrellas y en otras formas de radiación de banda muy ancha, como el campo de onda de punto cero del vacío electromagnético.
El comportamiento de la radiación EM y su interacción con la materia depende de su frecuencia y cambia cualitativamente a medida que cambia la frecuencia. Las frecuencias más bajas tienen longitudes de onda más largas y las frecuencias más altas tienen longitudes de onda más cortas y están asociadas con fotones de mayor energía. No se conoce un límite fundamental para estas longitudes de onda o energías, en ninguno de los extremos del espectro, aunque los fotones con energías cercanas a la energía de Planck o que la excedan (demasiado altas para haber sido observadas) requerirán nuevas teorías físicas para su descripción.
Radio y microondas
Cuando las ondas de radio inciden sobre un conductor, se acoplan al conductor, viajan a lo largo de él e inducen una corriente eléctrica en la superficie del conductor moviendo los electrones del material conductor en grupos de carga correlacionados. Dichos efectos pueden cubrir distancias macroscópicas en conductores (como antenas de radio), ya que la longitud de onda de las ondas de radio es larga.
Los fenómenos de radiación electromagnética con longitudes de onda que van desde un metro hasta un milímetro se denominan microondas; con frecuencias entre 300 MHz (0,3 GHz) y 300 GHz.
En frecuencias de radio y microondas, la EMR interactúa con la materia principalmente como una colección masiva de cargas que se distribuyen en una gran cantidad de átomos afectados. En los conductores eléctricos, dicho movimiento masivo inducido de cargas (corrientes eléctricas) da como resultado la absorción de la EMR, o bien separaciones de cargas que provocan la generación de nueva EMR (reflexión efectiva de la EMR). Un ejemplo es la absorción o emisión de ondas de radio por antenas, o la absorción de microondas por agua u otras moléculas con un momento dipolar eléctrico, como por ejemplo dentro de un horno de microondas. Estas interacciones producen corrientes eléctricas o calor, o ambos.
Infrarrojos
Al igual que la radio y las microondas, el infrarrojo (IR) también se refleja en los metales (y también en la mayoría de los EMR, en el rango ultravioleta). Sin embargo, a diferencia de la radiación de microondas y radio de baja frecuencia, la EMR infrarroja comúnmente interactúa con dipolos presentes en moléculas individuales, que cambian a medida que los átomos vibran en los extremos de un enlace químico único. En consecuencia, es absorbido por una amplia gama de sustancias, lo que hace que aumenten su temperatura a medida que las vibraciones se disipan en forma de calor. El mismo proceso, ejecutado a la inversa, hace que las sustancias a granel se irradien en el infrarrojo de forma espontánea (consulte la sección de radiación térmica a continuación).
La radiación infrarroja se divide en subregiones espectrales. Si bien existen diferentes esquemas de subdivisión, el espectro se suele dividir en infrarrojo cercano (0,75–1,4 μm), infrarrojo de longitud de onda corta (1,4–3 μm), infrarrojo de longitud de onda media (3–8 μm), infrarrojo de longitud de onda larga (8 –15 μm) e infrarrojo lejano (15–1000 μm).
Luz visible
Las fuentes naturales producen radiación EM en todo el espectro. La radiación EM con una longitud de onda entre aproximadamente 400 nm y 700 nm es detectada directamente por el ojo humano y percibida como luz visible. Otras longitudes de onda, especialmente el infrarrojo cercano (más de 700 nm) y el ultravioleta (más corto que 400 nm), a veces también se denominan luz.
A medida que la frecuencia aumenta al rango visible, los fotones tienen suficiente energía para cambiar la estructura de enlace de algunas moléculas individuales. No es casualidad que esto suceda en el rango visible, ya que el mecanismo de la visión implica el cambio en el enlace de una sola molécula, la retina, que absorbe un solo fotón. El cambio en la retina provoca un cambio en la forma de la proteína rodopsina que contiene, lo que inicia el proceso bioquímico que hace que la retina del ojo humano detecte la luz.
La fotosíntesis también es posible en este rango, por la misma razón. Una sola molécula de clorofila es excitada por un solo fotón. En los tejidos vegetales que realizan la fotosíntesis, los carotenoides actúan para extinguir la clorofila excitada electrónicamente producida por la luz visible en un proceso denominado extinción no fotoquímica, para evitar reacciones que de otro modo interferirían con la fotosíntesis a altos niveles de luz.
Los animales que detectan infrarrojos utilizan pequeños paquetes de agua que cambian de temperatura, en un proceso esencialmente térmico que involucra muchos fotones.
Se sabe que los infrarrojos, las microondas y las ondas de radio dañan las moléculas y los tejidos biológicos solo mediante el calentamiento masivo, no mediante la excitación de fotones individuales de la radiación.
La luz visible solo puede afectar a un pequeño porcentaje de todas las moléculas. Por lo general, no de forma permanente o dañina, sino que el fotón excita un electrón que luego emite otro fotón al regresar a su posición original. Esta es la fuente de color producida por la mayoría de los tintes. La retina es una excepción. Cuando se absorbe un fotón, la retina cambia permanentemente de estructura de cis a trans y requiere una proteína para convertirlo de nuevo, es decir, restablecerlo para que pueda funcionar como un detector de luz nuevamente.
Evidencia limitada indica que algunas especies reactivas de oxígeno son creadas por la luz visible en la piel y que pueden tener algún papel en el fotoenvejecimiento, de la misma manera que la luz ultravioleta A.
Ultravioleta
A medida que la frecuencia aumenta en el ultravioleta, los fotones ahora transportan suficiente energía (alrededor de tres electronvoltios o más) para excitar ciertas moléculas con doble enlace en un reordenamiento químico permanente. En el ADN, esto causa un daño duradero. El ADN también es dañado indirectamente por especies reactivas de oxígeno producidas por la luz ultravioleta A (UVA), que tiene una energía demasiado baja para dañar el ADN directamente. Esta es la razón por la que los rayos ultravioleta en todas las longitudes de onda pueden dañar el ADN, y es capaz de causar cáncer y (para los rayos UVB) quemaduras en la piel (quemaduras solares) que son mucho peores que las que se producirían por los simples efectos del calentamiento (aumento de la temperatura). Esta propiedad de causar daño molecular que está fuera de proporción con los efectos de calentamiento, es característica de todos los EMR con frecuencias en el rango de luz visible y superiores. Estas propiedades de la EMR de alta frecuencia se deben a los efectos cuánticos que dañan permanentemente los materiales y tejidos a nivel molecular.
En el extremo superior del rango ultravioleta, la energía de los fotones se vuelve lo suficientemente grande como para impartir suficiente energía a los electrones para que se liberen del átomo, en un proceso llamado fotoionización. La energía necesaria para esto siempre es superior a unos 10 electronvoltios (eV) correspondientes a longitudes de onda inferiores a 124 nm (algunas fuentes sugieren un límite más realista de 33 eV, que es la energía necesaria para ionizar el agua). Este extremo superior del espectro ultravioleta con energías en el rango de ionización aproximado, a veces se denomina "UV extremo". La radiación ultravioleta ionizante es fuertemente filtrada por la atmósfera terrestre.
Rayos X y rayos gamma
La radiación electromagnética compuesta por fotones que transportan energía de ionización mínima o más (que incluye todo el espectro con longitudes de onda más cortas), por lo tanto, se denomina radiación ionizante. (Muchos otros tipos de radiación ionizante están hechos de partículas que no son EM). La radiación ionizante de tipo electromagnético se extiende desde el ultravioleta extremo hasta todas las frecuencias más altas y longitudes de onda más cortas, lo que significa que todos los rayos X y gamma califican. Estos son capaces de los tipos más severos de daño molecular, lo que puede ocurrir en biología a cualquier tipo de biomolécula, incluidas mutaciones y cáncer, y a menudo a grandes profundidades debajo de la piel, ya que el extremo superior del espectro de rayos X y todos del espectro de rayos gamma, penetran la materia.
Atmósfera y magnetosfera
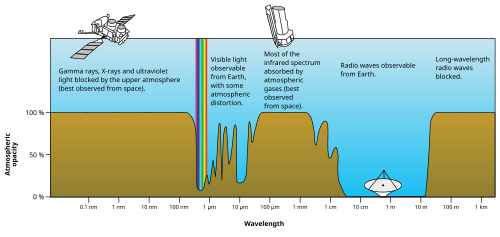
La mayoría de los rayos X y UV se bloquean primero por la absorción del nitrógeno molecular y luego (para las longitudes de onda en el UV superior) por la excitación electrónica del dioxígeno y, finalmente, por el ozono en el rango medio de UV. Solo el 30% de la luz ultravioleta del Sol llega al suelo, y casi toda esta se transmite bien.
La luz visible se transmite bien en el aire, ya que no tiene la energía suficiente para excitar el nitrógeno, el oxígeno o el ozono, pero sí demasiado para excitar las frecuencias vibratorias moleculares del vapor de agua.
Las bandas de absorción en el infrarrojo se deben a modos de excitación vibracional en el vapor de agua. Sin embargo, a energías demasiado bajas para excitar el vapor de agua, la atmósfera vuelve a ser transparente, lo que permite la libre transmisión de la mayoría de las ondas de microondas y de radio.
Por último, en longitudes de onda de radio de más de 10 m aproximadamente (alrededor de 30 MHz), el aire en la atmósfera inferior permanece transparente a la radio, pero el plasma en ciertas capas de la ionosfera comienza a interactuar con las ondas de radio (ver onda ionosférica). Esta propiedad permite que se reflejen algunas longitudes de onda más largas (100 m o 3 MHz) y da como resultado una radio de onda corta más allá de la línea de visión. Sin embargo, ciertos efectos ionosféricos comienzan a bloquear las ondas de radio entrantes desde el espacio, cuando su frecuencia es inferior a unos 10 MHz (longitud de onda superior a unos 30 m).
Radiación térmica y electromagnética como forma de calor
La estructura básica de la materia involucra partículas cargadas unidas entre sí. Cuando la radiación electromagnética incide sobre la materia, hace que las partículas cargadas oscilen y ganen energía. El destino final de esta energía depende del contexto. Podría volver a irradiarse inmediatamente y aparecer como radiación dispersa, reflejada o transmitida. Puede disiparse en otros movimientos microscópicos dentro de la materia, alcanzando el equilibrio térmico y manifestándose como energía térmica, o incluso energía cinética, en el material. Con algunas excepciones relacionadas con los fotones de alta energía (como la fluorescencia, la generación de armónicos, las reacciones fotoquímicas, el efecto fotovoltaico de las radiaciones ionizantes en el ultravioleta lejano, los rayos X y la radiación gamma), la radiación electromagnética absorbida simplemente deposita su energía al calentar el material.. Esto sucede con la radiación infrarroja, microondas y ondas de radio. Las ondas de radio intensas pueden quemar térmicamente el tejido vivo y pueden cocinar alimentos. Además de los láseres infrarrojos, los láseres visibles y ultravioleta suficientemente intensos pueden incendiar fácilmente el papel.
La radiación ionizante crea electrones de alta velocidad en un material y rompe los enlaces químicos, pero después de que estos electrones chocan muchas veces con otros átomos, eventualmente la mayor parte de la energía se convierte en energía térmica, todo en una pequeña fracción de segundo. Este proceso hace que la radiación ionizante sea mucho más peligrosa por unidad de energía que la radiación no ionizante. Esta advertencia también se aplica a los rayos UV, aunque casi todo no es ionizante, porque los rayos UV pueden dañar las moléculas debido a la excitación electrónica, que es mucho mayor por unidad de energía que los efectos de calentamiento.
La radiación infrarroja en la distribución espectral de un cuerpo negro generalmente se considera una forma de calor, ya que tiene una temperatura equivalente y está asociada con un cambio de entropía por unidad de energía térmica. Sin embargo, el "calor" es un término técnico en física y termodinámica y a menudo se confunde con energía térmica. Cualquier tipo de energía electromagnética puede transformarse en energía térmica en interacción con la materia. Así, cualquier radiación electromagnética puede "calentar" (en el sentido de aumentar la temperatura de la energía térmica de) un material, cuando se absorbe.
El proceso de absorción inverso o invertido en el tiempo es la radiación térmica. Gran parte de la energía térmica de la materia consiste en el movimiento aleatorio de partículas cargadas, y esta energía puede irradiarse fuera de la materia. La radiación resultante puede ser absorbida posteriormente por otra pieza de materia, con la energía depositada calentando el material.
La radiación electromagnética en una cavidad opaca en equilibrio térmico es efectivamente una forma de energía térmica, que tiene una entropía de radiación máxima.
Efectos biológicos
La bioelectromagnética es el estudio de las interacciones y los efectos de la radiación EM en los organismos vivos. Los efectos de la radiación electromagnética sobre las células vivas, incluidas las de los humanos, dependen de la potencia y la frecuencia de la radiación. Para la radiación de baja frecuencia (ondas de radio a la luz visible), los efectos mejor comprendidos son los que se deben únicamente a la potencia de la radiación, que actúa a través del calentamiento cuando se absorbe la radiación. Para estos efectos térmicos, la frecuencia es importante ya que afecta la intensidad de la radiación y la penetración en el organismo (por ejemplo, las microondas penetran mejor que el infrarrojo). Está ampliamente aceptado que los campos de baja frecuencia que son demasiado débiles para causar un calentamiento significativo no podrían tener ningún efecto biológico.
A pesar de los resultados comúnmente aceptados, se han llevado a cabo algunas investigaciones para demostrar que los campos electromagnéticos no térmicos más débiles (incluidos los campos magnéticos ELF débiles, aunque este último no califica estrictamente como radiación EM) y los campos electromagnéticos modulados Los campos de RF y microondas tienen efectos biológicos. Los mecanismos fundamentales de la interacción entre el material biológico y los campos electromagnéticos a niveles no térmicos no se conocen por completo.
La Organización Mundial de la Salud ha clasificado la radiación electromagnética de radiofrecuencia como Grupo 2B, posiblemente cancerígena. Este grupo contiene posibles carcinógenos como el plomo, el DDT y el estireno. Por ejemplo, los estudios epidemiológicos que buscan una relación entre el uso de teléfonos celulares y el desarrollo de cáncer cerebral no han sido concluyentes en gran medida, salvo para demostrar que el efecto, si existe, no puede ser grande.
A frecuencias más altas (visibles y más allá), los efectos de los fotones individuales comienzan a ser importantes, ya que ahora tienen suficiente energía individualmente para dañar directa o indirectamente las moléculas biológicas. Todas las frecuencias UV han sido clasificadas como carcinógenos del Grupo 1 por la Organización Mundial de la Salud. La radiación ultravioleta de la exposición al sol es la causa principal del cáncer de piel.
Por lo tanto, a frecuencias ultravioleta y superiores (y probablemente algo también en el rango visible), la radiación electromagnética causa más daño a los sistemas biológicos de lo que predice el simple calentamiento. Esto es más obvio en el "lejos" (o "extremo") ultravioleta. Los rayos UV, junto con los rayos X y la radiación gamma, se conocen como radiación ionizante debido a la capacidad de los fotones de esta radiación para producir iones y radicales libres en los materiales (incluido el tejido vivo). Dado que dicha radiación puede dañar gravemente la vida a niveles de energía que producen poco calentamiento, se considera mucho más peligrosa (en términos de daño producido por unidad de energía o potencia) que el resto del espectro electromagnético.
Usar como arma
El rayo de calor es una aplicación de EMR que utiliza frecuencias de microondas para crear un desagradable efecto de calentamiento en la capa superior de la piel. El ejército de los EE. UU. desarrolló un arma de rayos de calor conocida públicamente llamada Active Denial System como un arma experimental para negar el acceso del enemigo a un área. Un rayo de la muerte es un arma teórica que emite un rayo de calor basado en energía electromagnética a niveles que son capaces de dañar el tejido humano. Un inventor de un rayo de la muerte, Harry Grindell Matthews, afirmó haber perdido la vista en su ojo izquierdo mientras trabajaba en su arma de rayos de la muerte basada en un magnetrón de microondas de la década de 1920 (un horno de microondas normal crea un efecto de cocción que daña los tejidos dentro del horno en alrededor de 2 kV/m).
Derivación de la teoría electromagnética
Las leyes clásicas de la electricidad y el magnetismo, conocidas como ecuaciones de Maxwell, predicen las ondas electromagnéticas. Hay soluciones no triviales de las ecuaciones de Maxwell homogéneas (sin cargas ni corrientes), que describen ondas de campos eléctricos y magnéticos cambiantes. Comenzando con las ecuaciones de Maxwell en el espacio libre:
Silencio Silencio ⋅ ⋅ E=0{displaystyle nabla cdot mathbf {E} =0} | ()1) |
Silencio Silencio × × E=− − ∂ ∂ B∂ ∂ t{displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B}{partial t}} | ()2) |
Silencio Silencio ⋅ ⋅ B=0{displaystyle nabla cdot mathbf {B} =0} | ()3) |
Silencio Silencio × × B=μ μ 0ε ε 0∂ ∂ E∂ ∂ t{displaystyle nabla times mathbf {B} =mu} _{0}varepsilon {fnMicrosoft Sans Serif} {E} {fn} {fn}} {fn}}} {fn}} {fn}}} {fn}}} {fn}}}}}} {fn}}}}}}} {fn}}}} {f}}}}}}}}}}}}}} { | ()4) |
dónde
- E{displaystyle mathbf {E} y B{displaystyle mathbf {B} son el campo eléctrico (medido en V/m o N/C) y el campo magnético (medido en T o Wb/m)2), respectivamente;
- Silencio Silencio ⋅ ⋅ X{displaystyle nabla cdot mathbf {X} cede la divergencia y Silencio Silencio × × X{displaystyle nabla times mathbf {X} el borde de un campo vectorial X;{displaystyle mathbf {X}
- ∂ ∂ B∂ ∂ t{displaystyle {frac {partial mathbf {B}{partial t}} y ∂ ∂ E∂ ∂ t{displaystyle {frac {partial mathbf {E} {fn} {fn}} {fn}}} {fn}} {fn}}} {fn}}} {fn}}}}}} {fn}}}}}}} {fn}}}} {f}}}}}}}}}}}}}} { son derivados parciales (valor de cambio en el tiempo, con ubicación fija) del campo magnético y eléctrico;
- μ μ 0{displaystyle mu _{0}} es la permeabilidad de un vacío (4π × 10−7 (H/m)), y ε ε 0{displaystyle varepsilon ¿Qué? es la permitibilidad de un vacío (8.85×10−12 (F/m));
Además de la solución trivial
Tomando el rotacional de la segunda ecuación de Maxwell (2) se obtiene:
Silencio Silencio × × ()Silencio Silencio × × E)=Silencio Silencio × × ()− − ∂ ∂ B∂ ∂ t){displaystyle nabla times left(nabla times mathbf {E} right)=nabla times left(-{frac {partial mathbf {B}{partial t}right)}}} | ()5) |
Evaluando el lado izquierdo de (5) con la identidad anterior y simplificando usando (1), se obtiene:
Silencio Silencio × × ()Silencio Silencio × × E)=Silencio Silencio ()Silencio Silencio ⋅ ⋅ E)− − Silencio Silencio 2E=− − Silencio Silencio 2E.{displaystyle nabla times left(nabla times mathbf {E} right)=nabla left(nabla cdot mathbf {E} right)-nabla ^{2}mathbf {E} = 'nabla ^{2}mathbf {E} | ()6) |
Evaluar el lado derecho de (5) intercambiando la secuencia de derivaciones e insertando la cuarta ecuación de Maxwell (4), produce:
Silencio Silencio × × ()− − ∂ ∂ B∂ ∂ t)=− − ∂ ∂ ∂ ∂ t()Silencio Silencio × × B)=− − μ μ 0ε ε 0∂ ∂ 2E∂ ∂ t2{displaystyle nabla times left(-{frac {partial mathbf {B}{partial t}right)=-{frac {partial t}}left(nabla times mathbff {B} right)=-mu _{0}varepsilon {fnK} {fnMitbf} {f}} {f}}} {f}}}} | ()7) |
Combinando (6) y (7) nuevamente, se obtiene una ecuación diferencial con valores vectoriales para el campo eléctrico, resolviendo las ecuaciones homogéneas de Maxwell:
Silencio Silencio 2E=μ μ 0ε ε 0∂ ∂ 2E∂ ∂ t2{displaystyle nabla ^{2}mathbf {E} =mu} _{0}varepsilon {fnK} {fnMitbf} {fnK}} {f}}}}
Tomar el rotacional de la cuarta ecuación de Maxwell (4) da como resultado una ecuación diferencial similar para un campo magnético que resuelve las ecuaciones homogéneas de Maxwell:
Silencio Silencio 2B=μ μ 0ε ε 0∂ ∂ 2B∂ ∂ t2.{displaystyle nabla ^{2}mathbf {B} =mu} _{0}varepsilon ¿Qué? {B}{partial t^{2}}}
Ambas ecuaciones diferenciales tienen la forma de la ecuación general de ondas propagando con velocidad c0,{displaystyle c_{0},} Donde f{displaystyle f} es una función de tiempo y ubicación, que da la amplitud de la onda en algún momento en un determinado lugar:
Comparando los términos para la velocidad de propagación, se obtiene en el caso de los campos eléctrico y magnético:
Esta es la velocidad de la luz en vacío. Así las ecuaciones de Maxwell conectan la permitibilidad al vacío ε ε 0{displaystyle varepsilon ¿Qué?, la permeabilidad del vacío μ μ 0{displaystyle mu _{0}}, y la velocidad de la luz, c0, a través de la ecuación anterior. Esta relación había sido descubierta por Wilhelm Eduard Weber y Rudolf Kohlrausch antes del desarrollo de la electrodinámica de Maxwell, sin embargo Maxwell fue el primero en producir una teoría de campo consistente con olas que viajan a la velocidad de la luz.
Estas son solo dos ecuaciones frente a las cuatro originales, por lo que hay más información relacionada con estas ondas ocultas dentro de las ecuaciones de Maxwell. Una onda vectorial genérica para el campo eléctrico tiene la forma
Aquí, E0{displaystyle mathbf {E} _{0} es la amplitud constante, f{displaystyle f} es cualquier segunda función diferenciable, k^ ^ {displaystyle {hat {mathbf} } es un vector unitario en la dirección de la propagación, y x{displaystyle {mathbf {x}} es un vector de posición. f()k^ ^ ⋅ ⋅ x− − c0t){displaystyle f{hat {mathbf {k}}cdot mathbf {x} -c_{0}tright)}} es una solución genérica a la ecuación de onda. En otras palabras,
De la primera de las ecuaciones de Maxwell, obtenemos
Por lo tanto,
Por lo tanto,
Las ecuaciones restantes estarán satisfechas por esta elección de E,B{displaystyle mathbf {E}mathbf {B}.
Las ondas de campo eléctrico y magnético en el campo lejano viajan a la velocidad de la luz. Tienen una orientación restringida especial y una magnitud proporcional, E0=c0B0{displaystyle E_{0}=c_{0}B_{0}, que se puede ver inmediatamente desde el vector Poynting. El campo eléctrico, el campo magnético y la dirección de la propagación de ondas son todos ortogonales, y la onda se propaga en la misma dirección que E× × B{displaystyle mathbf {E} times mathbf {B}. También, E y B campos lejanos en el espacio libre, que como soluciones de onda dependen principalmente de estas dos ecuaciones de Maxwell, están en fase entre sí. Esto está garantizado ya que la solución de onda genérica es el primer orden tanto en el espacio como en el tiempo, y el operador de rizo en un lado de estas ecuaciones resulta en derivados espaciales de primera orden de la solución de onda, mientras que el tiempo-derivativo en el otro lado de las ecuaciones, que da el otro campo, es de primera orden en el tiempo, dando lugar al mismo cambio de fase para ambos campos en cada operación matemática.
Desde el punto de vista de una onda electromagnética que viaja hacia adelante, el campo eléctrico podría estar oscilando hacia arriba y hacia abajo, mientras que el campo magnético oscila hacia la derecha y hacia la izquierda. Esta imagen se puede girar con el campo eléctrico oscilando hacia la derecha y hacia la izquierda y el campo magnético oscilando hacia abajo y hacia arriba. Esta es una solución diferente que viaja en la misma dirección. Esta arbitrariedad en la orientación con respecto a la dirección de propagación se conoce como polarización. A nivel cuántico, se describe como polarización de fotones. La dirección de la polarización se define como la dirección del campo eléctrico.
Están disponibles formas más generales de las ecuaciones de onda de segundo orden dadas anteriormente, lo que permite fuentes y medios de propagación sin vacío. Existen muchas derivaciones en competencia, todas con diferentes niveles de aproximación y aplicaciones previstas. Un ejemplo muy general es una forma de la ecuación del campo eléctrico, que se factorizó en un par de ecuaciones de onda explícitamente direccionales y luego se redujo eficientemente a una sola ecuación de onda unidireccional por medio de una simple aproximación de evolución lenta.
Contenido relacionado
Dicroísmo
Jorge Ohm
Sólido amorfo