Punto antípoda

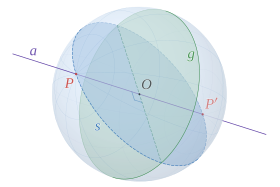
En matemáticas, dos puntos de una esfera (o n-esfera, incluido un círculo) se llaman antípodas o diametralmente opuestos si son las intersecciones de la esfera con un diámetro, una línea recta que pasa por su centro.

Dado cualquier punto en una esfera, su punto antípoda es el único punto a mayor distancia, ya sea medido intrínsecamente (distancia del círculo máximo en la superficie de la esfera) o extrínsecamente (distancia cordal a través del interior de la esfera). Cada círculo máximo de una esfera que pasa por un punto también pasa por su punto antípoda, y hay infinitos círculos máximos que pasan por un par de puntos antípodas (a diferencia de la situación de cualquier par de puntos no antípodas, que tienen un círculo máximo único pasando por ambos). Muchos resultados en geometría esférica dependen de la elección de puntos no antípodas y degeneran si se permiten puntos antípodas; por ejemplo, un triángulo esférico degenera a una luna poco especificada si dos de los vértices son antípodas.

El punto antípoda de un punto dado se llama antípodas, del griego ἀντίποδες (antípodes) que significa " pies opuestos"; ver Antípodas § Etimología. A veces se elimina la s y esto se representa como una antípoda, una formación posterior.

Matemáticas superiores

El concepto de puntos antípodas se generaliza a esferas de cualquier dimensión: dos puntos de la esfera son antípodas si son opuestos por el centro. Cada línea que pasa por el centro corta la esfera en dos puntos, uno por cada rayo que emana del centro, y estos dos puntos son antípodas.

El teorema Borsuk-Ulam es un resultado de la topología algebraica que trata con tales pares de puntos. Dice que cualquier función continua de Sn{displaystyle S^{n} a Rn{displaystyle mathbb {R} {} {}} {fn}} mapas algunos par de puntos antipodal en Sn{displaystyle S^{n} al mismo punto en Rn.{displaystyle mathbb {R} ^{n} Aquí, Sn{displaystyle S^{n} denota los n{displaystyle n}-dimensional y esferas Rn{displaystyle mathbb {R} {} {}} {fn}} es n{displaystyle n}-dimensional verdadero espacio de coordenadas.

El mapa antipodal A:Sn→ → Sn{displaystyle A:S^{n}to S^{n} envía cada punto en la esfera a su punto antipodal. Si puntos en el n{displaystyle n}- Esphere están representados como vectores de desplazamiento del centro de la esfera en Euclidean ()n+1){displaystyle (n+1)}- espacio, entonces dos puntos antipodales están representados por inversos aditivos v{displaystyle {Mathbf}} y − − v,{displaystyle -{mathbf {},} y el mapa antipodal se puede definir como A()x)=− − x.{displaystyle A({mathbf {x})=-{mathbf {x}} El mapa antipodal preserva la orientación (es homotopic al mapa de identidad) cuando n{displaystyle n} es extraño, y lo revierte cuando n{displaystyle n} es incluso. Su grado es ()− − 1)n+1.{displaystyle (-1)^{n+1}

Si se identifican puntos antípodas (considerados equivalentes), la esfera se convierte en un modelo de espacio proyectivo real.