Pulso ultracorto

En óptica, un pulso ultracorto, también conocido como evento ultrarrápido, es un pulso electromagnético cuya duración en el tiempo es del orden de un picosegundo (10 ⁻¹² segundos) o menos. Estos pulsos tienen un espectro óptico de banda ancha y pueden crearse mediante osciladores de modo bloqueado. La amplificación de pulsos ultracortos casi siempre requiere la técnica de amplificación de pulso chirriado, para evitar daños al medio de ganancia del amplificador.

Se caracterizan por una alta intensidad pico (o más correctamente, irradiación) que generalmente conduce a interacciones no lineales en diversos materiales, incluyendo el aire. Estos procesos se estudian en el campo de la óptica no lineal.

En la literatura especializada, "ultracorto" se refiere al rango de femtosegundos (fs) y picosegundos (ps), aunque estos pulsos ya no tienen el récord de los pulsos más cortos generados artificialmente. De hecho, se han informado pulsos de rayos X con duraciones en la escala de tiempo de attosegundos.

El Premio Nobel de Química de 1999 fue otorgado a Ahmed H. Zewail, por el uso de pulsos ultracortos para observar reacciones químicas en las escalas de tiempo en las que ocurren, abriendo el campo de la femtoquímica. También se concedió otro premio Nobel, el Premio Nobel de Física de 2023, por los pulsos ultracortos. Este premio fue otorgado a Pierre Agostini, Ferenc Krausz y Anne L'Huillier por el desarrollo de pulsos de attosegundos y su capacidad para estudiar la dinámica electrónica.

Definición

No existe una definición estándar de pulso ultracorto. Normalmente el atributo 'ultracorto' se aplica a pulsos con una duración de unas pocas decenas de femtosegundos, pero en un sentido más amplio, cualquier pulso que dure menos de unos pocos picosegundos puede considerarse ultracorto. La distinción entre "ultracortos" y "Ultrarápido" es necesario ya que la velocidad a la que se propaga el pulso es función del índice de refracción del medio a través del cual viaja, mientras que el pulso "ultracorto" se refiere al ancho temporal del paquete de ondas del pulso.

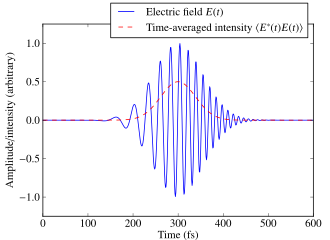
Un ejemplo común es un pulso gaussiano chirriado, una onda cuya amplitud de campo sigue una envolvente gaussiana y cuya fase instantánea tiene un barrido de frecuencia.

Fondo

El campo eléctrico real correspondiente a un pulso ultracorto oscila a una frecuencia angular ω₀ correspondiente a la longitud de onda central del pulso. Para facilitar los cálculos, se define un campo complejo E(t). Formalmente, se define como la señal analítica correspondiente al campo real.

La frecuencia angular central ω₀ generalmente se escribe explícitamente en el campo complejo, que puede separarse como una función de intensidad temporal I( t) y una función de fase temporal ψ(t):

E()t)=I()t)ei⋅ ⋅ 0tei↑ ↑ ()t){displaystyle E(t)={sqrt {I(t)}e^{iomega ¿Qué?

La expresión del complejo campo eléctrico en el dominio de frecuencia se obtiene de la transformación Fourier E()t):

E()⋅ ⋅ )=F()E()t)){displaystyle E(omega)={mathcal {F}(E(t)}

Debido a la presencia de la ei⋅ ⋅ 0t{displaystyle e^{iomega ¿Qué? termino, E()⋅) está centrado alrededor ⋅₀, y es una práctica común para referirse a E()⋅-⋅₀) por escribir sólo E()⋅), que haremos en el resto de este artículo.

Al igual que en el dominio del tiempo, en el dominio de la frecuencia se pueden definir una función de intensidad y una función de fase:

E()⋅ ⋅ )=S()⋅ ⋅ )eiφ φ ()⋅ ⋅ ){displaystyle E(omega)={sqrt {S(omega)}e^{iphi (omega)}}

La cantidad S()⋅ ⋅ ){displaystyle S(omega)} es potencia densidad espectral (o simplemente, el espectro espectro espectro espectro espectro espectro espectro espectro espectrodel pulso, y φ φ ()⋅ ⋅ ){displaystyle phi (omega)} es fase de densidad espectral (o simplemente fase espectral). Ejemplo de funciones de fase espectral incluyen el caso en que φ φ ()⋅ ⋅ ){displaystyle phi (omega)} es una constante, en cuyo caso el pulso se llama pulso limitado por ancho de banda, o donde φ φ ()⋅ ⋅ ){displaystyle phi (omega)} es una función cuadrática, en cuyo caso el pulso se llama pulso pulsado debido a la presencia de un barrido de frecuencia instantáneo. Tal chirpa se puede adquirir como un pulso se propaga a través de materiales (como vidrio) y se debe a su dispersión. Resulta en una ampliación temporal del pulso.

Funciones de intensidad: temporal I()t){displaystyle I(t)} y espectral S()⋅ ⋅ ){displaystyle S(omega)} —determine la duración del tiempo y el ancho de banda del espectro del pulso. Como se indica en el principio de incertidumbre, su producto (a veces llamado el producto ancho de tiempo) tiene un límite inferior. Este valor mínimo depende de la definición utilizada durante la duración y de la forma del pulso. Para un espectro dado, el producto de ancho de banda de tiempo mínimo, y por lo tanto el pulso más corto, se obtiene por un pulso limitado de transformación, es decir, para una fase espectral constante φ φ ()⋅ ⋅ ){displaystyle phi (omega)}. Los altos valores del producto de ancho de banda, por otro lado, indican un pulso más complejo.

Control de forma de pulso

Aunque los dispositivos ópticos que también se utilizan para luz continua, como expansores de haz y filtros espaciales, pueden usarse para pulsos ultracortos, varios dispositivos ópticos han sido diseñados específicamente para pulsos ultracortos. Uno de ellos es el compresor de pulsos, un dispositivo que permite controlar la fase espectral de pulsos ultracortos. Está compuesto por una secuencia de prismas o rejillas. Cuando se ajusta correctamente, puede alterar la fase espectral φ(ω) del pulso de entrada de modo que el pulso de salida sea un pulso de ancho de banda limitado con la duración más corta posible. Se puede utilizar un modelador de pulso para realizar modificaciones más complicadas tanto en la fase como en la amplitud de los pulsos ultracortos.

Para controlar con precisión el pulso, es imprescindible una caracterización completa de la fase espectral del pulso para obtener cierta fase espectral del pulso (como la limitada por transformación). Luego, se puede utilizar un modulador de luz espacial en el plano 4f para controlar el pulso. La exploración de fase de interferencia intrapulso multifotónica (MIIPS) es una técnica basada en este concepto. A través del escaneo de fase del modulador de luz espacial, MIIPS no solo puede caracterizar sino también manipular el pulso ultracorto para obtener la forma de pulso necesaria en el punto objetivo (como un pulso de transformación limitada para una potencia máxima optimizada y otras formas de pulso específicas). Si el modelador de pulso está completamente calibrado, esta técnica permite controlar la fase espectral de pulsos ultracortos utilizando una configuración óptica simple sin partes móviles. Sin embargo, la precisión de MIIPS es algo limitada con respecto a otras técnicas, como la puerta óptica con resolución de frecuencia (FROG).

Técnicas de medición

Hay varias técnicas disponibles para medir pulsos ópticos ultracortos.

La autocorrelación de intensidad proporciona el ancho del pulso cuando se asume una forma de pulso particular.

La interferometría espectral (SI) es una técnica lineal que se puede utilizar cuando se dispone de un pulso de referencia precaracterizado. Da la intensidad y la fase. El algoritmo que extrae la intensidad y la fase de la señal SI es directo. La interferometría de fase espectral para la reconstrucción directa del campo eléctrico (SPIDER) es una técnica de autorreferencia no lineal basada en la interferometría de corte espectral. El método es similar al SI, excepto que el pulso de referencia es una réplica espectralmente desplazada de sí mismo, lo que permite obtener la intensidad espectral y la fase del pulso de la sonda a través de una rutina de filtrado FFT directa similar al SI, pero que requiere la integración de la fase. extraído del interferograma para obtener la fase de pulso de la sonda.

La activación óptica por frecuencia resuelta (FROG) es una técnica no lineal que produce la intensidad y la fase de un pulso. Es una autocorrelación resuelta espectralmente. El algoritmo que extrae la intensidad y la fase de una traza FROG es iterativo. La observación sensata y eliminada por rejilla de campos electrónicos de luz láser incidente ultrarrápida (GRENOUILLE) es una versión simplificada de FROG. (Grenouille en francés significa "rana".)

Chirp scan es una técnica similar a MIIPS que mide la fase espectral de un pulso aplicando una rampa de fases espectrales cuadráticas y midiendo espectros de segundos armónicos. Con respecto a MIIPS, que requiere muchas iteraciones para medir la fase espectral, solo se necesitan dos exploraciones de chirrido para recuperar tanto la amplitud como la fase del pulso.

El escaneo de fase de interferencia intrapulso multifotónico (MIIPS) es un método para caracterizar y manipular el pulso ultracorto.

Propagación de paquetes de ondas en medios no isotrópicos

Para reiterar parcialmente la discusión anterior, la aproximación de sobres lentamente variable (SVEA) del campo eléctrico de una ola con vector de onda central K0{displaystyle {textbf}_{0}} y frecuencia central ⋅ ⋅ 0{displaystyle omega ¿Qué? del pulso, se da por:

E()x,t)=A()x,t)exp⁡ ⁡ ()iK0x− − i⋅ ⋅ 0t){displaystyle {textbf {} {textbf {x},t)={textbf {} {textbf {x}},t)exp(i{textbf {K}_{0}{textbf {x}-iomega _{0}t)}

Consideramos la propagación para el SVEA del campo eléctrico en un medio dispersivo homogéneo no isótropo. Asumiendo que el pulso se propaga en la dirección del eje z, se puede demostrar que el sobre A{displaystyle {textbf}} para uno de los casos más generales, a saber, un cristal biaxial, se rige por el PDE:

∂ ∂ A∂ ∂ z=− − β β 1∂ ∂ A∂ ∂ t− − i2β β 2∂ ∂ 2A∂ ∂ t2+16β β 3∂ ∂ 3A∂ ∂ t3+γ γ x∂ ∂ A∂ ∂ x+γ γ Sí.∂ ∂ A∂ ∂ Sí.{displaystyle {frac {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fn\fn\fnMicrosoft {\fnMicrosoft {\fn\\\\\fnMicrosoft {\\\\\fn\\\\\fnMicrosoft {\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\fnMicrosoft {\\\\fnMicrosoft {\\\\\\\\\fnMicrosoft {\\\\\\\\\\ {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { z}=~-~beta ###{1}{frac {partial {textbf {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { t}~-~{frac {I}{2}beta - ¿Qué? {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { {fnMicroc}beta ¿Qué? {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { ¿Por qué? {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { ##~+~gamma _{y}{frac {partial {textbf {} {fn} {fnK}}} {fn}}} {fn}} {fn}} {fn}}}} {fn}}}}} {fn}}}}}} {fn}}}}} {\fn}}}}}}}}}}}}}} {

+iγ γ tx∂ ∂ 2A∂ ∂ t∂ ∂ x+iγ γ tSí.∂ ∂ 2A∂ ∂ t∂ ∂ Sí.− − i2γ γ xx∂ ∂ 2A∂ ∂ x2− − i2γ γ Sí.Sí.∂ ∂ 2A∂ ∂ Sí.2+iγ γ xSí.∂ ∂ 2A∂ ∂ x∂ ∂ Sí.+⋯ ⋯ {displaystyle ~~~~~~~~~~~~ âTMagamma _{tx}{frac {partial ^{2}{textbf {A}}{partial tpartial tpartial ################################################################################################################################################################################################################################################################ ¿Por qué? {A}}{partial tpartial tpartial Y... {}{2}gamma _{xx}{frac {partial ^{2}{textbf {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { ### {2}~ {fnMicroc {I}{2}gamma ¿Por qué? {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { ¿Qué? ¿Por qué? {A}}{partial xpartial y}}+cdots }

donde los coeficientes contienen efectos de difracción y dispersión que se han determinado analíticamente con álgebra computarizada y verificada numéricamente al tercer orden para los medios isotrópicos y no isótrópicos, válidos en el campo cercano y en el campo lejano. β β 1{displaystyle beta ¿Qué? es el inverso de la proyección de la velocidad del grupo. El término en β β 2{displaystyle beta _{2} es la dispersión de velocidad de grupo (GVD) o dispersión de segundo orden; aumenta la duración del pulso y pulsa el pulso mientras se propaga a través del medio. El término en β β 3{displaystyle beta ¿Qué? es un término de dispersión de tercera orden que puede aumentar aún más la duración del pulso, incluso si β β 2{displaystyle beta _{2} desaparece. Los términos en γ γ x{displaystyle gamma _{x} y γ γ Sí.{displaystyle gamma _{y} describir el paso del pulso; el coeficiente γ γ x()γ γ Sí.){displaystyle gamma _{x}~(gamma _{y}} es la relación del componente de la velocidad del grupo x()Sí.){displaystyle x~(y)} y el vector de unidad en la dirección de la propagación del pulso (eje-z). Los términos en γ γ xx{displaystyle gamma _{xx} y γ γ Sí.Sí.{displaystyle gamma _{yyyy} describir la difusión del paquete de onda óptica en las direcciones perpendiculares al eje de propagación. Los términos en γ γ tx{displaystyle gamma _{tx} y γ γ tSí.{displaystyle gamma _{ty} que contiene derivados mixtos en el tiempo y el espacio giran el paquete de onda sobre el Sí.{displaystyle y} y x{displaystyle x} ejes, respectivamente, aumentar el ancho temporal del paquete de onda (además del aumento debido al GVD), aumentar la dispersión en el x{displaystyle x} y Sí.{displaystyle y} direcciones, respectivamente, y aumentar el chirp (además de eso β β 2{displaystyle beta _{2}) cuando este último y/o γ γ xx{displaystyle gamma _{xx} y γ γ Sí.Sí.{displaystyle gamma _{yyyy} no están desvanecendo. El término γ γ xSí.{displaystyle gamma _{xy}} gira el paquete de onda en el x− − Sí.{displaystyle x-y} avión. Poco a poco, debido a las expansiones previamente incompletas, esta rotación del pulso no se realizó hasta finales del decenio de 1990 pero ha sido experimentalmente confirmado. Para el tercer orden, el RHS de la ecuación anterior se encuentra tener estos términos adicionales para el caso de cristal uniaxial:

⋯ ⋯ +13γ γ txx∂ ∂ 3A∂ ∂ x2∂ ∂ t+13γ γ tSí.Sí.∂ ∂ 3A∂ ∂ Sí.2∂ ∂ t+13γ γ ttx∂ ∂ 3A∂ ∂ t2∂ ∂ x+⋯ ⋯ {displaystyle cdots ~+~{1}{3}gamma _{txx}{frac {partial ^{3}{textbf {A}}{partial x^{2}partial . {1}{3}gamma ¿Por qué? {A} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}}} {f}}} {fn}}} {fnMicrosoft}}}}}} {fnMicrosoft}}}}}} {f}}}}}}}}}}} { - ¿Qué? . {1}{3}gamma ¿Qué? {A}} {partial t^{2}partial }+cdots }

Los términos primero y segundo son responsables de la curvatura del frente propagante del pulso. These terms, including the term in β β 3{displaystyle beta ¿Qué? están presentes en un medio isotrópico y representan la superficie esférica de un frente propagante originario de una fuente de punto. El término γ γ txx{displaystyle gamma _{txx} se puede expresar en términos del índice de refracción, la frecuencia ⋅ ⋅ {displaystyle omega } y sus derivados y el término γ γ ttx{displaystyle gamma _{ttx} también distorsiona el pulso pero de una manera que revierte los roles de t{displaystyle t} y x{displaystyle x} (ver referencia de Trippenbach, Scott y Band para detalles). Hasta ahora, el tratamiento aquí es lineal, pero los términos dispersivos no lineales son omnipresentes a la naturaleza. Estudios relativos a un nuevo término no lineal γ γ nlSilencioASilencio2A{displaystyle gamma _{nl} han demostrado que tales términos tienen un efecto profundo en el paquete de ondas, incluyendo entre otras cosas, un autoestablecimiento del paquete de ondas. Los aspectos no lineales eventualmente conducen a solitones ópticos.

A pesar de ser bastante común, la SVEA no es necesaria para formular una simple ecuación de onda que describa la propagación de pulsos ópticos. De hecho, como se muestra en, incluso una forma muy general de la ecuación de onda electromagnética de segundo orden puede ser factorizada en componentes direccionales, proporcionando acceso a una ecuación de onda de primer orden para el campo en sí, en lugar de un sobre. Esto requiere sólo una suposición de que la evolución del campo es lenta en la escala de una longitud de onda, y no restringe el ancho de banda del pulso en absoluto, como lo demuestra vívidamente.

Altos armónicos

Los pulsos ultrashortes de alta energía se pueden generar a través de alta generación armónica en un medio no lineal. Un pulso ultracorte de alta intensidad generará una serie de armónicos en el medio; una armónica particular de interés se selecciona con un monocromador. Esta técnica se ha utilizado para producir pulsos ultracortados en los regímenes ultravioleta y de rayos X ultra suaves de pulsos láser de zafiro casi infrarrojos.

Aplicaciones

Microprocesamiento/nanoprocesamiento 3D de materiales avanzado

La capacidad de los láseres de femtosegundos para fabricar eficientemente estructuras y dispositivos complejos para una amplia variedad de aplicaciones se ha estudiado ampliamente durante la última década. Se pueden utilizar técnicas de procesamiento láser de última generación con pulsos de luz ultracortos para estructurar materiales con una resolución submicrométrica. La escritura láser directa (DLW) de fotoprotectores adecuados y otros medios transparentes puede crear complejos cristales fotónicos tridimensionales (PhC), componentes microópticos, rejillas, andamios de ingeniería de tejidos (TE) y guías de ondas ópticas. Estas estructuras son potencialmente útiles para potenciar aplicaciones de próxima generación en telecomunicaciones y bioingeniería que dependen de la creación de piezas en miniatura cada vez más sofisticadas. La precisión, la velocidad de fabricación y la versatilidad del procesamiento láser ultrarrápido lo sitúan en una buena posición para convertirse en una herramienta industrial vital para la fabricación.

Micromecanizado

Entre las aplicaciones del láser de femtosegundo, se ha experimentado con la microtexturización de las superficies de los implantes para mejorar la formación de hueso alrededor de los implantes dentales de circonio. La técnica demostró ser precisa con un daño térmico muy bajo y con la reducción de los contaminantes superficiales. Estudios posteriores en animales demostraron que el aumento de la capa de oxígeno y las micro y nanocaracterísticas creadas por la microtexturización con láser de femtosegundo dieron como resultado tasas más altas de formación ósea, mayor densidad ósea y estabilidad mecánica mejorada.