Puerta XOR
| Input | Producto | |
| A | B | Un XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Puerta XOR (a veces EORo EXOR y pronunciadas como Exclusivo) es una puerta lógica digital que da una salida verdadera (1 o ALTO) cuando el número de entradas verdaderas es extraño. Una puerta XOR implementa una exclusiva o () de la lógica matemática; es decir, un verdadero resultado de salida si uno, y sólo uno, de las entradas a la puerta es verdad. Si ambas entradas son falsas (0/LOW) o ambas son verdaderas, un falso resultado de salida. XOR representa la función de desigualdad, es decir, la salida es verdadera si las entradas no son iguales de lo contrario la salida es falsa. Una manera de recordar XOR es "deber tener uno o el otro pero no ambos".
Una compuerta XOR puede funcionar como un "inversor programable" en el que una entrada determina si se debe invertir la otra entrada o simplemente pasarla sin cambios. Por lo tanto, funciona como un inversor (una compuerta NOT) que puede activarse o desactivarse mediante un interruptor.
La operación XOR también puede considerarse como una suma módulo 2. Por ello, las puertas XOR se utilizan para implementar la suma binaria en las computadoras. Un semisumador consta de una puerta XOR y una puerta AND. La puerta también se utiliza en sustractores y comparadores.
Las expresiones algebraicas o o o todos representan la puerta XOR con entradas A y B. El comportamiento de XOR se resume en la tabla de la verdad mostrada sobre la derecha.
Símbolos
Existen tres símbolos esquemáticos para las puertas XOR: los símbolos ANSI y DIN tradicionales y el símbolo IEC. En algunos casos, el símbolo DIN se utiliza con ⊕ en lugar de ≢. Para obtener más información, consulte Símbolos de puertas lógicas.
El símbolo "=1" en el IEC indica que la salida se activa únicamente con una entrada activa.
 |  | 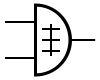 | ||
| Símbolo esquemático ANSI XOR | Símbolo esquemático de la CEI | Símbolo esquema XOR |
Los símbolos lógicos ⊕, Jpq y ⊻ se pueden utilizar para indicar una operación XOR en expresiones algebraicas.
Los lenguajes similares a C utilizan el símbolo de intercalación ^ para indicar una operación XOR a nivel de bits. (Tenga en cuenta que el símbolo de intercalación no indica una conjunción lógica (AND) en estos lenguajes, a pesar de la similitud de los símbolos).
Implementación
La compuerta XOR se implementa con mayor frecuencia mediante circuitos MOSFET. Algunas de esas implementaciones incluyen:
Y-O-Invertir
Las puertas XOR se pueden implementar utilizando lógica AOI.
- Una puerta XOR usando una puerta 2-2 OR-AND-Invert y entradas negadas.
- Una puerta XOR usando una puerta de 2-1 AND-OR-Invert.
A continuación se muestran las implementaciones de semiconductor de óxido metálico (CMOS) de la compuerta XOR correspondiente a la lógica AOI anterior.
A la izquierda se organizan los transistores nMOS y pMOS para que los pares de entrada y activar los 2 transistores pMOS de la parte superior izquierda o los 2 transistores pMOS de la parte superior derecha respectivamente, conectando Vdd a la salida para una lógica alta. Los pares de entrada restantes y activa cada uno de los dos caminos nMOS en el fondo a Vss para una lógica baja.
Si hay entradas invertidas (por ejemplo, desde un flip-flop) disponibles, esta puerta se puede utilizar directamente. De lo contrario, se necesitan dos inversores adicionales con dos transistores cada uno para generar y , trayendo el número total de transistores a doce.
La implementación de AOI sin entrada invertida se ha utilizado, por ejemplo, en la CPU Intel 386.
- Ejemplo de puerta CMOS XOR
- Puerta CMOS XOR usando AOI-Logic
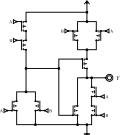
Puertas de transmisión
La compuerta XOR también se puede implementar mediante el uso de compuertas de transmisión con lógica de transistor de paso.

Esta implementación utiliza dos puertas de transmisión y dos inversores no mostrados en el diagrama para generar y para un total de ocho transistores, cuatro menos que en el diseño anterior. La función XOR se implementa pasando a la salida el valor invertido de A cuando B es alto y pasando el valor de A cuando B está en una lógica baja. Así que cuando ambas entradas son bajas la puerta de transmisión en la parte inferior está apagada y la que está en la parte superior y permite A a través de la cual es baja por lo que la salida es baja. Cuando ambos son altos sólo el que está en el fondo es activo y permite el valor invertido de A a través y ya que A es alto la salida será nuevamente baja. Del mismo modo si B se mantiene alto pero A es bajo el producto sería que es alto como se espera y si B es bajo pero A es alto el valor de A pasa a través y la salida es alta completando la tabla de la verdad para la puerta XOR.
La desventaja de la implementación anterior es que, dado que las puertas de transmisión no son interruptores ideales, tienen una resistencia asociada, por lo que, dependiendo de la intensidad de la señal de entrada, conectarlas en cascada puede degradar los niveles de salida.
Cableado optimizado de lógica de paso-puerta
La aplicación anterior de la puerta de transmisión puede ser optimizada aún más de ocho a seis transistores mediante la implementación de la funcionalidad del inversor que genera y el pase inferior con sólo dos transistores dispuestos como un inversor pero con la fuente del pMOS conectado a en lugar de Vdd y la fuente del NMOS conectado a en lugar de GND.

Los dos transistores más izquierdistas mencionados anteriormente, realizan una inversión condicional optimizada de A cuando B está en una lógica alta usando la lógica transistor de paso para reducir el recuento transistor y cuando B está en una lógica baja, su salida está en un estado de alta impedancia. Los dos en el centro son una puerta de transmisión que conduce la salida al valor de A cuando B está en una lógica baja y los dos transistores más rectos forman un inversor necesario para generar utilizado por la puerta de transmisión y el circuito de lógica transistor de paso.
Al igual que con la aplicación anterior, se debe tener en cuenta la conexión directa de las entradas a las salidas a través de los transistores de las puertas de paso o a través de los dos transistores más izquierdistas, especialmente cuando las en cascada.
Alternativas

Si un tipo específico de puerta no está disponible, un circuito que implementa la misma función puede ser construido a partir de otras puertas disponibles. Un circuito que implementa una función XOR puede ser construido trivialmente a partir de una puerta XNOR seguido de una puerta NO. Si consideramos la expresión , podemos construir un circuito de puertas XOR directamente utilizando Y, OR y NO puertas. Sin embargo, este enfoque requiere cinco puertas de tres tipos diferentes.
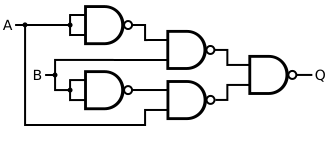
Como alternativa, si diferentes puertas están disponibles podemos aplicar álgebra booleana para transformar como se indicó anteriormente, y aplicar la Ley de Morgan al último término para obtener que se puede implementar utilizando sólo cuatro puertas como se muestra en la derecha. intuitivamente, XOR es equivalente a OR excepto cuando ambos A y B son altos. Así que el AND del OR con entonces NAND que da un bajo sólo cuando ambos A y B son altos es equivalente al XOR.
Se puede realizar un circuito de compuerta XOR a partir de cuatro compuertas NAND. De hecho, tanto las compuertas NAND como las NOR son las llamadas "compuertas universales" y cualquier función lógica se puede construir a partir de lógica NAND o lógica NOR únicamente. Si se reemplazan las cuatro compuertas NAND por compuertas NOR, se obtiene una compuerta XNOR, que se puede convertir en una compuerta XOR invirtiendo la salida o una de las entradas (por ejemplo, con una quinta compuerta NOR).
| Puerta deseada | Construcción NAND | Construcción NOR |
|---|---|---|
 |  | 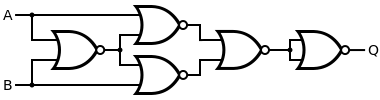 |
Un arreglo alternativo es de cinco puertas NOR en una topología que enfatiza la construcción de la función desde , notando de la Ley de Morgan que una puerta NOR es una entrada y puerta invertida. Otro arreglo alternativo es de cinco puertas NAND en una topología que enfatiza la construcción de la función desde , notando de la Ley de Morgan que una puerta NAND es una puerta de entrada o entrada invertida.
| Puerta deseada | Construcción NAND | Construcción NOR |
|---|---|---|
 |  |  |
Para las construcciones NAND, la disposición superior requiere menos puertas. Para las construcciones NOR, la disposición inferior ofrece la ventaja de un retardo de propagación más corto (el retardo de tiempo entre el cambio de una entrada y el cambio de la salida).
Paquetes de chip estándar

Los chips XOR están disponibles fácilmente. Los códigos estándar más comunes son:
- 4070: CMOS cuádruples doble entrada puertas XOR.
- 4030: CMOS cuádruples doble entrada puertas XOR.
- 7486: TTL cuádruple doble entrada puertas XOR.
Más de dos entradas
La interpretación literal del nombre "o exclusivo", o la observación del símbolo rectangular IEC, plantea la cuestión del comportamiento correcto con entradas adicionales. Si una puerta lógica aceptara tres o más entradas y produjera una salida verdadera si exactamente una de esas entradas fuera verdadera, entonces sería en efecto un detector one-hot (y de hecho este es el caso para solo dos entradas). Sin embargo, rara vez se implementa de esta manera en la práctica.
Lo más común es considerar que las entradas subsiguientes se aplican a través de una cascada de operaciones binarias exclusivas: las dos primeras señales se introducen en una compuerta XOR, luego la salida de esa compuerta se introduce en una segunda compuerta XOR junto con la tercera señal, y así sucesivamente para las señales restantes. El resultado es un circuito que genera un 1 cuando el número de 1 en sus entradas es impar, y un 0 cuando el número de 1 entrantes es par. Esto lo hace prácticamente útil como generador de paridad o sumador módulo 2.
Por ejemplo, el microchip 74LVC1G386 se anuncia como una puerta lógica de tres entradas, e implementa un generador de paridad.
Aplicaciones
Las puertas XOR y las puertas AND son las dos estructuras más utilizadas en aplicaciones VLSI.
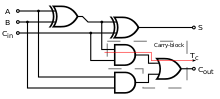
Adición
La compuerta lógica XOR se puede utilizar como un sumador de un bit que suma dos bits cualesquiera para obtener un bit de salida. Por ejemplo, si sumamos 1 más 1 en binario, esperamos una respuesta de dos bits, 10 (es decir, 2 en decimal). Dado que el bit de suma final en esta salida se logra con XOR, el bit de acarreo anterior se calcula con una compuerta AND. Este es el principio principal de los sumadores a medias. Se puede encadenar un circuito sumador completo ligeramente más grande para sumar números binarios más largos.
En ciertas situaciones, las entradas de una compuerta OR (por ejemplo, en un sumador completo) o de una compuerta XOR nunca pueden ser ambas 1. Como esta es la única combinación en la que difieren las salidas de las compuertas OR y XOR, una compuerta OR puede reemplazarse por una compuerta XOR (o viceversa) sin alterar la lógica resultante. Esto es conveniente si el circuito se está implementando utilizando chips de circuitos integrados simples que contienen solo un tipo de compuerta por chip.
Generador de números pseudoaleatorios

Los generadores de números pseudoaleatorios (PRN), específicamente los registros de desplazamiento con retroalimentación lineal (LFSR), se definen en términos de la operación exclusiva-o. Por lo tanto, una configuración adecuada de puertas XOR puede modelar un registro de desplazamiento con retroalimentación lineal para generar números aleatorios.
Detectores de fase
Las puertas XOR se pueden utilizar en los detectores de fase más simples.
Almacenar en búfer o invertir una señal
Se puede utilizar una compuerta XOR para cambiar fácilmente entre el almacenamiento en búfer o la inversión de una señal. Por ejemplo, se pueden agregar compuertas XOR a la salida de un circuito decodificador de pantalla de siete segmentos para permitir que un usuario elija entre una salida activa baja o activa alta.
Correlación y detección de secuencias
Las puertas XOR producen un 0 cuando ambas entradas coinciden. Cuando se busca un patrón de bits específico o una secuencia PRN en una secuencia de datos muy larga, se puede utilizar una serie de puertas XOR para comparar una cadena de bits de la secuencia de datos con la secuencia de destino en paralelo. Luego se puede contar la cantidad de salidas 0 para determinar qué tan bien coincide la secuencia de datos con la secuencia de destino. Los correladores se utilizan en muchos dispositivos de comunicaciones, como receptores y decodificadores CDMA, para corrección de errores y códigos de canal. En un receptor CDMA, los correladores se utilizan para extraer la polaridad de una secuencia PRN específica de una colección combinada de secuencias PRN.
Un correlacionador que busque 11010 en la secuencia de datos 1110100101 compararía los bits de datos entrantes con la secuencia de destino en cada desplazamiento posible mientras cuenta la cantidad de coincidencias (ceros):
1110100101 (datos) 11010 (objetivo) 00111 (XOR) 2 bits cero 1110100101 11010 00000 5 bits cero 1110100101 11010 01110 2 bits cero 1110100101 11010 10011 2 bits cero 1110100101 11010 01000 4 bits cero 1110100101 11010 11111 0 cero bits Coincidencias por offset: . :: ::: --------- 0 1 2 3 4 5
En este ejemplo, la mejor coincidencia se produce cuando la secuencia de destino está desplazada por 1 bit y los cinco bits coinciden. Cuando está desplazada por 5 bits, la secuencia coincide exactamente con su inversa. Al observar la diferencia entre la cantidad de unos y ceros que salen del banco de puertas XOR, es fácil ver dónde se produce la secuencia y si está invertida o no. Las secuencias más largas son más fáciles de detectar que las secuencias cortas.
Representación analítica
es una representación analítica de la puerta XOR:
es una representación analítica alternativa.