Puerta de toffoli

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Puerta de lógica reversible universal, aplicada en computación cuántica

En circuitos lógicos, la puerta de Toffoli (también puerta CCNOT), inventada por Tommaso Toffoli, es una puerta lógica reversible universal, lo que significa que cualquier circuito reversible clásico puede construirse a partir de puertas Toffoli. También se le conoce como el método "controlado-controlado-no" puerta, que describe su acción. Dispone de entradas y salidas de 3 bits; si los dos primeros bits están configurados en 1, se invierte el tercer bit; de lo contrario, todos los bits permanecen iguales.

Antecedentes

Una puerta lógica L que consume entradas es reversible si cumple las siguientes condiciones: L(x) = y es una puerta donde para cualquier salida y, hay una entrada única x. La puerta L es reversible si hay una puerta L′(y) = x que asigna y a x. Desde las puertas lógicas comunes, NOT es reversible, como se puede ver en la tabla de verdad a continuación.

INPUT	OUTPUT
0	1
1	0

La puerta AND común no es reversible, porque las entradas 00, 01 y 10 están asignadas a la salida 0.

Las puertas reversibles se han estudiado desde la década de 1960. La motivación original fue que las puertas reversibles disipan menos calor (o, en principio, nada de calor).

La motivación más reciente proviene de la computación cuántica. En mecánica cuántica el estado cuántico puede evolucionar de dos maneras, mediante la ecuación de Schrödinger (transformaciones unitarias) o mediante su colapso. Las operaciones lógicas para computadoras cuánticas, de las cuales la puerta de Toffoli es un ejemplo, son transformaciones unitarias y, por lo tanto, evolucionan de manera reversible.

Universalidad y puerta de Toffoli

Cualquier puerta reversible que consuma sus entradas y permita todos los cálculos de entrada no debe tener más bits de entrada que bits de salida, según el principio del casillero. Para un bit de entrada, hay dos posibles puertas reversibles. Uno de ellos NO lo es. La otra es la puerta de identidad, que asigna su entrada a la salida sin cambios. Para dos bits de entrada, la única puerta no trivial es la puerta NOT controlada, que realiza un XOR del primer bit al segundo bit y deja el primer bit sin cambios.

Tabla de la verdad

Forma de matriz de permutación

INPUT		OUTPUT
0	0	0	0
0	1	0	1
1	0	1	1
1	1	1	0

${begin{bmatrix}1&0&0&0\0&1&0&0\0&0&0&1\0&0&1&0\end{bmatrix}}$

Desafortunadamente, hay funciones reversibles que no se pueden calcular usando solo esas puertas. En otras palabras, el conjunto formado por las puertas NOT y XOR no es universal. Para calcular una función arbitraria utilizando puertas reversibles, se necesita otra puerta. Una posibilidad es la puerta de Toffoli, propuesta en 1980 por Toffoli.

Esta puerta tiene entradas y salidas de 3 bits. Si los dos primeros bits están configurados, invierte el tercer bit. La siguiente es una tabla de los bits de entrada y salida:

Tabla de la verdad

Forma de matriz de permutación

INPUT			OUTPUT
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	0	1
1	1	0	1	1	1
1	1	1	1	1	0

$begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \ end{bmatrix}$

También se puede describir como bits de mapeo {a, b, c} a {a, b, c XOR (a AND b)}. Esto también se puede entender como una operación Modulo en bit c: {a, b, c} → {a, b, $(c+ab) mod. 2$ } a menudo escrito como {a, b, c} → {a, b, c $oplus$ ab

La puerta Toffoli es universal; esto significa que para cualquier función booleana f(x₁, x₂,..., x_m), hay un circuito formado por las puertas de Toffoli que toma x₁, x₂,..., x_m y algunos bits adicionales establecidos en 0 o 1 para las salidas x₁, x₂,..., x_m, f(x₁, x₂,..., x_m), y algunos bits adicionales (llamado basura). Una puerta NOT, por ejemplo, se puede construir a partir de una puerta Toffoli estableciendo los tres bits de entrada en {a, 1, 1}, haciendo que el tercer bit de salida (1 XOR (a AND 1)) = NOT a; (a Y b) es el tercer bit de salida de {a, b, 0}. Básicamente, esto significa que se pueden utilizar puertas de Toffoli para construir sistemas que realicen cualquier cálculo de función booleana deseada de forma reversible.

Puertas lógicas relacionadas

La puerta de Fredkin es una puerta reversible universal de 3 bits que intercambia los dos últimos bits si el primer bit es 1; una operación de intercambio controlado.
El n-bit Toffoli gate es una generalización de la puerta Toffoli. Toma. n bits x₁, x₂,... x_n como insumos y productos n bits. La primera n−1 bits de salida son sólo x₁,... x_n−1. El último bit de salida es (x₁ Y... Y x_n−1XOR x_n.
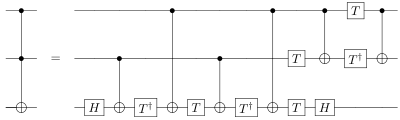
La puerta de Toffoli se puede realizar por cinco puertas cuánticas de dos codos, pero se puede demostrar que no es posible utilizar menos de cinco.

Una puerta cuántica relacionada, la puerta Deutsch, se puede realizar por cinco pulsos ópticos con átomos neutros. La puerta del Deutsch es una puerta universal para el cálculo cuántico.
La puerta de Margolus (nombrada después de Norman Margolus), también llamada Toffoli simplificada es una puerta lógica cuántica muy similar a una puerta de Toffoli pero con un -1 en la diagonal: ${displaystyle mathrm {RCCX} =operatorname {diag} (1,1,1,1,1,-1,X)}$ . La puerta de Margolus también es universal para circuitos reversibles y actúa muy similar a una puerta Toffoli, con la ventaja de que se puede construir con cerca de la mitad de los CNOTS en comparación con la puerta de Toffoli.

Relación con la computación cuántica

Cualquier puerta reversible se puede implementar en una computadora cuántica y, por lo tanto, la puerta de Toffoli también es un operador cuántico. Sin embargo, la puerta de Toffoli no se puede utilizar para el cálculo cuántico universal, aunque sí significa que una computadora cuántica puede implementar todos los cálculos clásicos posibles. La puerta de Toffoli debe implementarse junto con algunas puertas inherentemente cuánticas para que sea universal para la computación cuántica. De hecho, cualquier puerta de un solo qubit con coeficientes reales que pueda crear un estado cuántico no trivial es suficiente. En enero de 2009 se realizó con éxito una puerta de Toffoli basada en la mecánica cuántica en la Universidad de Innsbruck, Austria. Mientras que la implementación de un n-qubit Toffoli con modelo de circuito requiere 2n puertas CNOT, el límite superior más conocido se sitúa en 6n – 12 Puertas CNOT. Se ha sugerido que las computadoras Ion Quantum atrapadas pueden implementar una puerta Toffoli n-qubit directamente. La aplicación de la interacción de muchos cuerpos podría usarse para la operación directa de la puerta en iones atrapados, átomos de Rydberg e implementaciones de circuitos superconductores. Siguiendo la variedad de estado oscuro, la puerta Khazali-Mølmer C_n-NOT opera con solo tres pulsos, apartándose del paradigma del modelo de circuito.

Más resultados...