Pruebas de hipótesis estadísticas
Una prueba de hipótesis estadística es un método de inferencia estadística que se utiliza para decidir si los datos disponibles respaldan suficientemente una hipótesis en particular. La prueba de hipótesis nos permite hacer afirmaciones probabilísticas sobre los parámetros de la población.
Historia
Uso temprano
Si bien la prueba de hipótesis se popularizó a principios del siglo XX, las primeras formas se utilizaron en el siglo XVIII. El primer uso se atribuye a John Arbuthnot (1710), seguido de Pierre-Simon Laplace (década de 1770), al analizar la proporción de sexos humanos al nacer; ver § Proporción sexual humana.
Orígenes modernos y controversia temprana
Las pruebas de significancia modernas son en gran medida el producto de Karl Pearson (valor p, prueba chi-cuadrado de Pearson), William Sealy Gosset (distribución t de Student) y Ronald Fisher ("hipótesis nula", análisis de varianza, "prueba de significancia"), mientras que la prueba de hipótesis fue desarrollada por Jerzy Neyman y Egon Pearson (hijo de Karl). Ronald Fisher comenzó su vida en estadística como un bayesiano (Zabell 1992), pero Fisher pronto se desilusionó con la subjetividad involucrada (a saber, el uso del principio de indiferencia al determinar las probabilidades previas) y buscó proporcionar un enfoque más "objetivo". 34; enfoque de la inferencia inductiva.
Fisher hizo hincapié en métodos y diseños experimentales rigurosos para extraer un resultado de pocas muestras asumiendo distribuciones gaussianas. Neyman (quien se asoció con el joven Pearson) enfatizó el rigor matemático y los métodos para obtener más resultados de muchas muestras y una gama más amplia de distribuciones. La prueba de hipótesis moderna es un híbrido inconsistente de la formulación, los métodos y la terminología de Fisher vs Neyman/Pearson desarrollados a principios del siglo XX.
Fisher popularizó la "prueba de significancia". Requería una hipótesis nula (correspondiente a una distribución de frecuencias de la población) y una muestra. Sus cálculos (ahora familiares) determinaron si rechazar o no la hipótesis nula. Las pruebas de significación no utilizaron una hipótesis alternativa, por lo que no existía el concepto de un error de tipo II.
El valor p se diseñó como un índice informal, pero objetivo, destinado a ayudar a un investigador a determinar (en base a otros conocimientos) si modificar experimentos futuros o fortalecer la fe en uno. la hipótesis nula. Neyman y Pearson idearon la prueba de hipótesis (y los errores de tipo I/II) como una alternativa más objetiva al valor p de Fisher, también destinado a determinar el comportamiento del investigador, pero sin requerir ningún tipo de inducción. inferencia por parte del investigador.
Neyman &erio; Pearson consideró un problema diferente al de Fisher (al que llamaron "prueba de hipótesis"). Inicialmente consideraron dos hipótesis simples (ambas con distribuciones de frecuencia). Calcularon dos probabilidades y, por lo general, seleccionaron la hipótesis asociada con la probabilidad más alta (la hipótesis con mayor probabilidad de haber generado la muestra). Su método siempre seleccionaba una hipótesis. También permitió el cálculo de ambos tipos de probabilidades de error.
Fisher y Neymar/Pearson se enfrentaron amargamente. Neyman/Pearson consideraron que su formulación era una generalización mejorada de las pruebas de significancia (el artículo definitorio era abstracto; los matemáticos han generalizado y refinado la teoría durante décadas). Fisher pensó que no era aplicable a la investigación científica porque a menudo, durante el transcurso del experimento, se descubre que las suposiciones iniciales sobre la hipótesis nula son cuestionables debido a fuentes de error inesperadas. Creía que el uso de decisiones rígidas de rechazo/aceptación basadas en modelos formulados antes de recopilar los datos era incompatible con este escenario común que enfrentan los científicos y los intentos de aplicar este método a la investigación científica conducirían a una gran confusión.
La disputa entre Fisher y Neyman–Pearson se libró por motivos filosóficos, caracterizados por un filósofo como una disputa sobre el papel adecuado de los modelos en la inferencia estadística.
Los acontecimientos intervinieron: Neyman aceptó un puesto en la Universidad de California, Berkeley en 1938, rompiendo su asociación con Pearson y separando a los disputantes (que habían ocupado el mismo edificio) por gran parte del diámetro planetario. La Segunda Guerra Mundial proporcionó un intermedio en el debate. La disputa entre Fisher y Neyman terminó (sin resolver después de 27 años) con la muerte de Fisher en 1962. Neyman escribió un elogio bien considerado. Algunas de las publicaciones posteriores de Neyman informaron valores p y niveles de significación.
La versión moderna de la prueba de hipótesis es un híbrido de los dos enfoques que resultaron de la confusión de los escritores de libros de texto de estadística (como predijo Fisher) a partir de la década de 1940 (pero la detección de señales, por ejemplo, todavía usa la formulación de Neyman/Pearson). Se ignoraron grandes diferencias conceptuales y muchas salvedades además de las mencionadas anteriormente. Neyman y Pearson proporcionaron la terminología más fuerte, las matemáticas más rigurosas y la filosofía más consistente, pero el tema que se enseña hoy en la estadística introductoria tiene más similitudes con el método de Fisher que con el de ellos.
Alrededor de 1940, los autores de libros de texto de estadística comenzaron a combinar los dos enfoques mediante el uso del valor p en lugar de la estadística de prueba (o datos) para contrastarla con el modelo de Neyman-Pearson "nivel de significación".
| # | Pruebas de hipótesis nula de Fisher | Neyman-Pearson teoría de la decisión |
|---|---|---|
| 1 | Establecer una hipótesis nula estadística. El nulo no necesita ser una hipótesis nula (es decir, cero diferencia). | Establecer dos hipótesis estadísticas, H1 y H2, y decidir sobre α, β y tamaño de muestra antes del experimento, sobre la base de consideraciones subjetivas de costo-beneficio. Estos definen una región de rechazo para cada hipótesis. |
| 2 | Informe el nivel exacto de significado (por ejemplo p = 0,051 o p = 0,049). No use un nivel convencional del 5%, y no hable de aceptar o rechazar hipótesis. Si el resultado es "no significativo", no sacar conclusiones y no tomar decisiones, pero suspender el juicio hasta que se disponga de más datos. | Si los datos entran en la región de rechazo de H1, acepte H2; de otro modo acepte H1. Aceptar una hipótesis no significa que creas en ella, pero sólo que actúas como si fuera verdad. |
| 3 | Use este procedimiento sólo si se sabe poco sobre el problema a la mano, y sólo para sacar conclusiones provisionales en el contexto de un intento de entender la situación experimental. | La utilidad del procedimiento se limita entre otros a situaciones donde usted tiene una disyunción de hipótesis (por ejemplo, μ1 = 8 o μ2 = 10 es verdad) y donde usted puede hacer cambios significativos costo-beneficio para elegir alfa y beta. |
Primeras elecciones de hipótesis nula
Paul Meehl ha argumentado que la importancia epistemológica de la elección de la hipótesis nula no ha sido reconocida en gran medida. Cuando la teoría predice la hipótesis nula, un experimento más preciso será una prueba más severa de la teoría subyacente. Cuando la hipótesis nula por defecto es "sin diferencia" o "sin efecto", un experimento más preciso es una prueba menos severa de la teoría que motivó la realización del experimento. Por lo tanto, puede ser útil un examen de los orígenes de esta última práctica:
1778: Pierre Laplace compara las tasas de natalidad de niños y niñas en varias ciudades europeas. Afirma: "es natural concluir que estas posibilidades están casi en la misma proporción". De ahí la hipótesis nula de Laplace de que las tasas de natalidad de niños y niñas deberían ser iguales dada la 'sabiduría convencional'.
1900: Karl Pearson desarrolla la prueba de chi cuadrado para determinar "si una determinada forma de curva de frecuencia describirá efectivamente las muestras extraídas de una población determinada". Así, la hipótesis nula es que una población está descrita por alguna distribución predicha por la teoría. Utiliza como ejemplo los números de cinco y seises en los datos de lanzamiento de dados de Weldon.
1904: Karl Pearson desarrolla el concepto de "contingencia" para determinar si los resultados son independientes de un factor categórico dado. Aquí, la hipótesis nula es por defecto que dos cosas no están relacionadas (por ejemplo, la formación de cicatrices y las tasas de mortalidad por viruela). La hipótesis nula en este caso ya no es predicha por la teoría o la sabiduría convencional, sino que es el principio de indiferencia que llevó a Fisher y a otros a descartar el uso de "probabilidades inversas".
Filosofía
La prueba de hipótesis y la filosofía se cruzan. La estadística inferencial, que incluye la prueba de hipótesis, es probabilidad aplicada. Tanto la probabilidad como su aplicación están entrelazadas con la filosofía. El filósofo David Hume escribió: "Todo conocimiento degenera en probabilidad". Las definiciones prácticas de probabilidad que compiten reflejan diferencias filosóficas. La aplicación más común de la prueba de hipótesis está en la interpretación científica de datos experimentales, que naturalmente es estudiado por la filosofía de la ciencia.
Fisher y Neymar se opusieron a la subjetividad de la probabilidad. Sus puntos de vista contribuyeron a las definiciones objetivas. El núcleo de su desacuerdo histórico era filosófico.
Muchas de las críticas filosóficas de la prueba de hipótesis son discutidas por estadísticos en otros contextos, particularmente la correlación no implica causalidad y el diseño de experimentos. La prueba de hipótesis es de interés continuo para los filósofos.
Educación
La estadística se enseña cada vez más en las escuelas y la prueba de hipótesis es uno de los elementos que se enseñan. Muchas conclusiones reportadas en la prensa popular (encuestas de opinión política hasta estudios médicos) se basan en estadísticas. Algunos escritores han afirmado que el análisis estadístico de este tipo permite pensar con claridad sobre los problemas que involucran datos masivos, así como el informe efectivo de tendencias e inferencias a partir de dichos datos, pero advierten que los escritores para un público amplio deben tener una comprensión sólida del campo. para utilizar correctamente los términos y conceptos. Una clase introductoria de estadística universitaria pone mucho énfasis en la prueba de hipótesis, quizás la mitad del curso. Campos como la literatura y la divinidad ahora incluyen hallazgos basados en análisis estadísticos (ver el Analizador de la Biblia). Una clase de introducción a la estadística enseña la prueba de hipótesis como un proceso de libro de cocina. La prueba de hipótesis también se enseña a nivel de posgrado. Los estadísticos aprenden a crear buenos procedimientos de prueba estadística (como z, Student's t, F y chi-squared). La prueba de hipótesis estadísticas se considera un área madura dentro de las estadísticas, pero continúa un desarrollo limitado.
Un estudio académico afirma que el método de libro de cocina para enseñar estadística introductoria no deja tiempo para la historia, la filosofía o la controversia. La prueba de hipótesis se ha enseñado como método unificado recibido. Las encuestas mostraron que los graduados de la clase estaban llenos de conceptos erróneos filosóficos (sobre todos los aspectos de la inferencia estadística) que persistían entre los instructores. Si bien el problema se abordó hace más de una década y continúan los llamados a la reforma educativa, los estudiantes aún se gradúan de las clases de estadística con conceptos erróneos fundamentales sobre la prueba de hipótesis. Las ideas para mejorar la enseñanza de la prueba de hipótesis incluyen alentar a los estudiantes a buscar errores estadísticos en los artículos publicados, enseñar la historia de la estadística y enfatizar la controversia en un tema generalmente seco.
El proceso de prueba
En la literatura estadística, la prueba de hipótesis estadísticas juega un papel fundamental. Hay dos procesos matemáticamente equivalentes que se pueden utilizar.
La línea habitual de razonamiento es la siguiente:
- Hay una hipótesis de investigación inicial de la que se desconoce la verdad.
- El primer paso es indicar lo relevante nulo y hipótesis alternativas. Esto es importante, ya que el mal estado de las hipótesis enfurecerá el resto del proceso.
- El segundo paso es considerar los supuestos estadísticos que se están haciendo sobre la muestra al hacer el examen; por ejemplo, hipótesis sobre la independencia estadística o sobre la forma de las distribuciones de las observaciones. Esto es igualmente importante ya que las suposiciones inválidas significarán que los resultados de la prueba son inválidos.
- Decidir qué prueba es apropiada, y declarar el pertinente prueba estadística T.
- Deducir la distribución de la estadística de prueba bajo la hipótesis nula de las suposiciones. En casos estándar este será un resultado bien conocido. Por ejemplo, la estadística de prueba podría seguir la distribución t de un estudiante con grados conocidos de libertad, o una distribución normal con medios conocidos y varianza. Si la distribución de la estadística de prueba está completamente fijada por la hipótesis nula llamamos la hipótesis simple, de lo contrario se llama composite.
- Seleccione un nivel de significado (α), un umbral de probabilidad debajo del cual la hipótesis nula será rechazada. Los valores comunes son 5% y 1%.
- La distribución de la estadística de prueba bajo la hipótesis nula particiones los posibles valores de T en aquellos por los que se rechaza la hipótesis nula: región crítica- y aquellos por los que no lo es. La probabilidad de la región crítica es α. En el caso de una hipótesis nula compuesta, la probabilidad máxima de la región crítica es α.
- Computar de las observaciones el valor observado tobs de la estadística de prueba T.
- Decide rechazar la hipótesis nula a favor de la alternativa o no rechazarla. La regla de la decisión es rechazar la hipótesis nula H0 si el valor observado tobs está en la región crítica, y no rechazar la hipótesis nula de otra manera.
Una formulación alternativa común de este proceso es la siguiente:
- Computar de las observaciones el valor observado tobs de la estadística de prueba T.
- Calcular el valor p. Esta es la probabilidad, bajo la hipótesis nula, de muestrear una estadística de prueba al menos tan extrema como la que se observó (la probabilidad máxima de ese evento, si la hipótesis es compuesta).
- Rechazar la hipótesis nula, a favor de la hipótesis alternativa, si y sólo si la p- el valor es inferior a (o igual a) el nivel de significación (la probabilidad seleccionada) umbral (α), por ejemplo 0.05 o 0.01.
El primer proceso era ventajoso en el pasado cuando solo estaban disponibles tablas de estadísticas de prueba en umbrales de probabilidad comunes. Permitía tomar una decisión sin el cálculo de una probabilidad. Era adecuado para el trabajo en clase y para uso operativo, pero era deficiente para reportar resultados. Este último proceso se basó en tablas extensas o en soporte computacional no siempre disponible. El cálculo explícito de una probabilidad es útil para informar. Los cálculos ahora se realizan de forma trivial con el software apropiado.
La diferencia en los dos procesos aplicados al ejemplo de la maleta radiactiva (abajo):
- "La lectura de Geiger-counter es 10. El límite es 9. Revisa la maleta."
- "La lectura de Geiger-counter es alta; el 97% de las maletas seguras tienen menor lectura. El límite es del 95%. Revisa la maleta."
El primer informe es adecuado, el segundo da una explicación más detallada de los datos y el motivo por el cual se revisa la maleta.
No rechazar la hipótesis nula no significa que la hipótesis nula sea "aceptada" (ver la sección de Interpretación).
Los procesos descritos aquí son perfectamente adecuados para la computación. Descuidan seriamente las consideraciones de diseño de experimentos.
Es particularmente importante que se calculen los tamaños de muestra apropiados antes de realizar el experimento.
La frase "prueba de significación" fue acuñado por el estadístico Ronald Fisher.
Interpretación
El valor p es la probabilidad de que un resultado dado (o un resultado más significativo) ocurra bajo la hipótesis nula. A un nivel de significación de 0,05, se esperaría que una moneda justa rechazara (incorrectamente) la hipótesis nula (que es justa) en aproximadamente 1 de cada 20 pruebas. El valor p no proporciona la probabilidad de que la hipótesis nula o su contraria sean correctas (una fuente común de confusión).
Si el valor p es menor que el umbral de significancia elegido (de manera equivalente, si la estadística de prueba observada está en la región crítica), entonces decimos que la hipótesis nula se rechaza en el nivel elegido de significado. Si el valor de p no es menor que el umbral de significancia elegido (de manera equivalente, si la estadística de prueba observada está fuera de la región crítica), entonces no se rechaza la hipótesis nula.
En el ejemplo de La dama probando té (abajo), Fisher le pidió a la Dama que categorizara correctamente todas las tazas de té para justificar la conclusión de que era poco probable que el resultado se deba al azar. Su prueba reveló que si la mujer estaba adivinando al azar (la hipótesis nula), había un 1,4 % de probabilidad de que se produjeran los resultados observados (té perfectamente ordenado).
Rechazar la hipótesis de que una gran huella de pata se originó en un oso no prueba de inmediato la existencia de Bigfoot. La prueba de hipótesis enfatiza el rechazo, que se basa en una probabilidad, en lugar de la aceptación.
"La probabilidad de rechazar la hipótesis nula es una función de cinco factores: si la prueba es de una o dos colas, el nivel de significación, la desviación estándar, la cantidad de desviación de la hipótesis nula, y el número de observaciones."
Uso e importancia
Las estadísticas son útiles para analizar la mayoría de las colecciones de datos. Esto es igualmente cierto para las pruebas de hipótesis que pueden justificar conclusiones incluso cuando no existe una teoría científica. En el ejemplo de la Dama probando té, era "obvio" que no existía diferencia entre (leche vertida en té) y (té vertido en leche). Los datos contradecían lo "obvio".
Las aplicaciones del mundo real de las pruebas de hipótesis incluyen:
- Probando si más hombres que mujeres sufren de pesadillas
- Establecer la autoría de los documentos
- Evaluando el efecto de la luna llena en el comportamiento
- Determinando el rango en el que un murciélago puede detectar un insecto por eco
- Decidir si la alfombra hospitalaria resulta en más infecciones
- Seleccionar los mejores medios para dejar de fumar
- Comprobando si las pegatinas de parachoques reflejan el comportamiento del propietario del coche
- Probando las afirmaciones de analistas de escritura
La prueba de hipótesis estadísticas juega un papel importante en el conjunto de las estadísticas y en la inferencia estadística. Por ejemplo, Lehmann (1992) en una revisión del artículo fundamental de Neyman y Pearson (1933) dice: “Sin embargo, a pesar de sus defectos, el nuevo paradigma formulado en el artículo de 1933 y los muchos desarrollos llevados a cabo dentro de su marco continúan desempeñando un papel central tanto en la teoría como en la práctica de las estadísticas y se puede esperar que lo haga en un futuro previsible.
Las pruebas de significancia han sido la herramienta estadística preferida en algunas ciencias sociales experimentales (más del 90 % de los artículos en el Journal of Applied Psychology a principios de la década de 1990). Otros campos han favorecido la estimación de parámetros (por ejemplo, tamaño del efecto). Las pruebas de significación se utilizan como sustituto de la comparación tradicional del valor predicho y el resultado experimental en el centro del método científico. Cuando la teoría solo es capaz de predecir el signo de una relación, se puede configurar una prueba de hipótesis direccional (unilateral) para que solo un resultado estadísticamente significativo respalde la teoría. Esta forma de evaluación de la teoría es la aplicación más criticada de la prueba de hipótesis.
Precauciones
"Si el gobierno exigiera que los procedimientos estadísticos llevaran etiquetas de advertencia como las de las drogas, la mayoría de los métodos de inferencia tendrían etiquetas largas." Esta precaución se aplica a las pruebas de hipótesis y sus alternativas.
La prueba de hipótesis exitosa está asociada con una probabilidad y una tasa de error tipo I. La conclusión podría estar equivocada.
La conclusión de la prueba es tan sólida como la muestra en la que se basa. El diseño del experimento es fundamental. Se han observado una serie de efectos inesperados que incluyen:
- El efecto Hans inteligente. Un caballo parecía ser capaz de hacer aritmética simple.
- El efecto Hawthorne. Los trabajadores industriales eran más productivos en una mejor iluminación, y más productivos en peor.
- El efecto placebo. Las pilas sin ingredientes médicos activos fueron notablemente eficaces.
Un análisis estadístico de datos engañosos produce conclusiones engañosas. El problema de la calidad de los datos puede ser más sutil. En la previsión, por ejemplo, no hay acuerdo sobre una medida de la precisión de la previsión. En ausencia de una medición consensuada, ninguna decisión basada en mediciones estará libre de controversia.
Sesgo de publicación: es menos probable que se publiquen resultados estadísticamente no significativos, lo que puede sesgar la literatura.
Múltiples pruebas: cuando se realizan varias pruebas de hipótesis nulas verdaderas a la vez sin ajuste, la probabilidad general de error de tipo I es mayor que el nivel alfa nominal.
Aquellos que toman decisiones críticas basadas en los resultados de una prueba de hipótesis son prudentes al observar los detalles en lugar de solo la conclusión. En las ciencias físicas, la mayoría de los resultados se aceptan por completo solo cuando se confirman de forma independiente. El consejo general con respecto a las estadísticas es: "Las cifras nunca mienten, pero los mentirosos calculan" (anónimo).
Definición de términos
Las siguientes definiciones se basan principalmente en la exposición del libro de Lehmann y Romano:
- Hipótesis estadística: Una declaración sobre los parámetros que describen una población (no una muestra).
- Prueba estadística: Un valor calculado a partir de una muestra sin parámetros desconocidos, a menudo para resumir la muestra con fines de comparación.
- Hipótesis simple: Cualquier hipótesis que especifique la distribución de la población por completo.
- Hipótesis compuesta: Cualquier hipótesis que haga no especificar la distribución de la población completamente.
- Hipótesis nula (H)0)
- Datos positivos: Datos que permiten al investigador rechazar una hipótesis nula.
- Hipótesis alternativa (H)1)
- Región de rechazo / Región crítica: El conjunto de valores de la estadística de prueba para la cual se rechaza la hipótesis nula.
- Valor crítico
- Potencia de una prueba (1 -β)
- Tamaño: Para hipótesis simples, esta es la probabilidad de la prueba incorrectamente rechazando la hipótesis nula. El falso índice positivo. Para las hipótesis compuestas este es el supremum de la probabilidad de rechazar la hipótesis nula sobre todos los casos cubiertos por la hipótesis nula. El complemento de la tasa positiva falsa se denomina especificidad en bioestadística. ("Esta es una prueba específica. Debido a que el resultado es positivo, podemos decir con confianza que el paciente tiene la condición.") Véase sensibilidad y especificidad y errores tipo I y tipo II para definiciones exhaustivas.
- Nivel de significación de una prueba (α)
- p-value
- Prueba de significación estadística: Antecesor de la prueba de hipótesis estadística (ver la sección Origen). Se dijo que un resultado experimental era estadísticamente significativo si una muestra era suficientemente inconsistente con la hipótesis (null). Esto se consideró de manera diferente el sentido común, una heurística pragmática para identificar resultados experimentales significativos, una convención que establece un umbral de evidencia estadística o un método para sacar conclusiones de los datos. La prueba de hipótesis estadística añadió rigor matemático y consistencia filosófica al concepto haciendo explícita la hipótesis alternativa. El término se utiliza flojamente para la versión moderna que ahora forma parte de la prueba de hipótesis estadística.
- Prueba conservadora: Una prueba es conservadora si, cuando se construye para un nivel nominal dado, la verdadera probabilidad de incorrectamente rechazar la hipótesis nula nunca es mayor que el nivel nominal.
- Prueba de salida
Una prueba de hipótesis estadística compara una estadística de prueba (z o t por ejemplo) con un umbral. La estadística de prueba (la fórmula que se encuentra en la siguiente tabla) se basa en la optimización. Para un nivel fijo de tasa de error Tipo I, el uso de estas estadísticas minimiza las tasas de error Tipo II (equivalente a maximizar la potencia). Los siguientes términos describen las pruebas en términos de tal optimización:
- Prueba más poderosa: Para un dado tamaño o nivel de significación, la prueba con el mayor poder (probabilidad de rechazo) para un valor dado del parámetro(s) que se está probando, contenida en la hipótesis alternativa.
- Prueba uniformemente más potente (UMP)
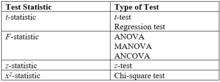
Estadísticas de prueba comunes
Ejemplos
Proporción sexual humana
El primer uso de la prueba de hipótesis estadística generalmente se atribuye a la cuestión de si los nacimientos masculinos y femeninos son igualmente probables (hipótesis nula), que fue abordada en la década de 1700 por John Arbuthnot (1710) y más tarde por Pierre-Simon Laplace. (década de 1770).
Arbuthnot examinó los registros de nacimiento en Londres para cada uno de los 82 años desde 1629 hasta 1710 y aplicó la prueba de signos, una prueba no paramétrica simple. En todos los años, el número de hombres nacidos en Londres superó el número de mujeres. Si se consideran igualmente probables más nacimientos masculinos o femeninos, la probabilidad del resultado observado es de 0,582, o aproximadamente 1 en 4 836 000 000 000 000 000 000 000; en términos modernos, este es el valor p. Arbuthnot llegó a la conclusión de que esto es demasiado pequeño para deberse al azar y, en cambio, debe deberse a la providencia divina: "De donde se sigue que es el arte, no el azar, el que gobierna". En términos modernos, rechazó la hipótesis nula de nacimientos masculinos y femeninos igualmente probables en el nivel de significancia p = 1/282.
Laplace consideró las estadísticas de casi medio millón de nacimientos. Las estadísticas mostraron un exceso de niños en comparación con las niñas. Concluyó mediante el cálculo de un valor p que el exceso era un efecto real, pero no explicado.
Señora saboreando té
En un famoso ejemplo de prueba de hipótesis, conocido como La dama probando té, la Dra. Muriel Bristol, una colega de Fisher, afirmó poder saber si se agregó primero el té o la leche. a una taza Fisher propuso darle ocho tazas, cuatro de cada variedad, en orden aleatorio. Entonces, uno podría preguntar cuál era la probabilidad de que obtuviera el número correcto, pero solo por casualidad. La hipótesis nula era que la Dama no tenía tal habilidad. La estadística de prueba fue un simple conteo del número de éxitos en la selección de las 4 copas. La región crítica fue el caso único de 4 aciertos de 4 posibles en base a un criterio de probabilidad convencional (< 5%). Un patrón de 4 aciertos corresponde a 1 de 70 combinaciones posibles (p≈ 1,4%). Fisher afirmó que (nunca) se requirió ninguna hipótesis alternativa. La señora identificó correctamente cada taza, lo que se consideraría un resultado estadísticamente significativo.
Juicio en la corte
Un procedimiento de prueba estadística es comparable a un juicio penal; un acusado se considera no culpable mientras no se pruebe su culpabilidad. El fiscal trata de probar la culpabilidad del acusado. Solo cuando hay suficientes pruebas para la acusación, el acusado es condenado.
En el comienzo del procedimiento, hay dos hipótesis : "el acusado no es culpable", y "El acusado es culpable". El primero, , se llama el hipótesis nula. El segundo, , se llama el hipótesis alternativas. Es la hipótesis alternativa que uno espera apoyar.
La hipótesis de inocencia se rechaza solo cuando es muy poco probable que se produzca un error, porque no se quiere condenar a un acusado inocente. Tal error se llama error de primer tipo (es decir, la condena de una persona inocente), y la ocurrencia de este error se controla para que sea rara. Como consecuencia de este comportamiento asimétrico, un error del segundo tipo (absolver a una persona que cometió el delito), es más común.
| H0 es verdad Verdaderamente inocente | H1 es verdad Verdaderamente culpable | |
|---|---|---|
| No rechazar la hipótesis nula Acusación | Decisión correcta | Decisión incorrecta Error tipo II |
| Hipótesis de null Condena | Decisión incorrecta Error tipo I | Decisión correcta |
Un juicio penal se puede considerar como uno de los dos procesos de decisión, o ambos: culpable frente a no culpable o evidencia frente a un umbral ("más allá de una duda razonable"). En un punto de vista, el acusado es juzgado; en el otro punto de vista, se juzga el desempeño de la acusación (que tiene la carga de la prueba). Una prueba de hipótesis puede considerarse como un juicio de una hipótesis o como un juicio de evidencia.
Frijoles filosóficos
El siguiente ejemplo fue producido por un filósofo que describía métodos científicos generaciones antes de que se probaran las hipótesis. formalizado y popularizado.
Pocos frijoles de este puñado son blancos.
La mayoría de frijoles en esta bolsa son blancos.
Por lo tanto: Probablemente, estos frijoles fueron tomados de otra bolsa.
Es una inferencia hipotética.
Los frijoles en la bolsa son la población. Los puñados son la muestra. La hipótesis nula es que la muestra se originó a partir de la población. El criterio para rechazar la hipótesis nula es el "obvio" diferencia en apariencia (una diferencia informal en la media). El resultado interesante es que la consideración de una población real y una muestra real produjo una bolsa imaginaria. El filósofo estaba considerando la lógica en lugar de la probabilidad. Para ser una prueba de hipótesis estadística real, este ejemplo requiere las formalidades de un cálculo de probabilidad y una comparación de esa probabilidad con un estándar.
Una generalización simple del ejemplo considera una bolsa mixta de frijoles y un puñado que contiene muy pocos o muchos frijoles blancos. La generalización considera ambos extremos. Se requieren más cálculos y más comparaciones para llegar a una respuesta formal, pero la filosofía central no ha cambiado; Si la composición del puñado es muy diferente a la de la bolsa, entonces la muestra probablemente se originó en otra bolsa. El ejemplo original se denomina prueba unilateral o de una cola, mientras que la generalización se denomina prueba bilateral o de dos colas.
La declaración también se basa en la inferencia de que el muestreo fue aleatorio. Si alguien hubiera estado rebuscando en la bolsa para encontrar frijoles blancos, entonces explicaría por qué el puñado tenía tantos frijoles blancos y también explicaría por qué se agotó la cantidad de frijoles blancos en la bolsa (aunque probablemente se supone que la bolsa mucho más grande que la mano).
Juego de cartas Clarividente
Se prueba la clarividencia de una persona (el sujeto). Se les muestra el reverso de un naipe elegido al azar 25 veces y se les pregunta a cuál de los cuatro palos pertenece. El número de aciertos, o respuestas correctas, se llama X.
Mientras tratamos de encontrar evidencia de su clarividencia, por el momento la hipótesis nula es que la persona no es clarividente. La alternativa es: la persona es (más o menos) clarividente.
Si la hipótesis nula es válida, lo único que puede hacer la persona que realiza la prueba es adivinar. Para cada carta, la probabilidad (frecuencia relativa) de que aparezca un solo palo es 1/4. Si la alternativa es válida, el sujeto de la prueba pronosticará correctamente el palo con una probabilidad superior a 1/4. Llamaremos a la probabilidad de acertar p. Las hipótesis, entonces, son:
- hipótesis nula (sólo adivinando)
y
- hipótesis alternativas (true clairvoyant).
Cuando el sujeto de prueba predice correctamente las 25 cartas, lo consideraremos clarividente y rechazaremos la hipótesis nula. Así también con 24 o 23 aciertos. Con solo 5 o 6 aciertos, en cambio, no hay motivo para considerarlos así. Pero, ¿qué pasa con 12 hits o 17 hits? ¿Cuál es el número crítico, c, de aciertos, en qué punto consideramos que el sujeto es clarividente? ¿Cómo determinamos el valor crítico c? Con la opción c=25 (es decir, solo aceptamos la clarividencia cuando todas las cartas se pronostican correctamente) somos más críticos que con c=10. En el primer caso, casi ningún sujeto de prueba será reconocido como clarividente, en el segundo caso, un cierto número pasará la prueba. En la práctica, uno decide qué tan crítico será. Es decir, uno decide con qué frecuencia acepta un error del primer tipo: un falso positivo o error de Tipo I. Con c = 25 la probabilidad de tal error es:
y por lo tanto, muy pequeño. La probabilidad de un falso positivo es la probabilidad de acertar al azar las 25 veces.
Siendo menos crítico, con c=10, da:
Por lo tanto, c = 10 produce una probabilidad mucho mayor de falso positivo.
Antes de realizar la prueba, se determina la probabilidad máxima aceptable de un error de tipo I (α). Típicamente, se seleccionan valores en el rango de 1% a 5%. (Si la tasa de error máxima aceptable es cero, se requiere un número infinito de conjeturas correctas). Según esta tasa de error de Tipo 1, se calcula el valor crítico c. Por ejemplo, si seleccionamos una tasa de error del 1%, c se calcula así:
De todos los números c, con esta propiedad, elegimos el más pequeño, para minimizar la probabilidad de un error tipo II, un falso negativo. Por ejemplo, seleccionamos: .
Maleta radiactiva
Como ejemplo, considere determinar si una maleta contiene algún material radiactivo. Colocado debajo de un contador Geiger, produce 10 conteos por minuto. La hipótesis nula es que no hay material radiactivo en la maleta y que todos los recuentos medidos se deben a la radiactividad ambiental típica del aire circundante y objetos inofensivos. Entonces podemos calcular la probabilidad de que observemos 10 conteos por minuto si la hipótesis nula fuera cierta. Si la hipótesis nula predice (digamos) un promedio de 9 conteos por minuto, entonces, de acuerdo con la distribución de Poisson típica para la desintegración radiactiva, hay alrededor del 41% de posibilidades de registrar 10 o más conteos. Por lo tanto, podemos decir que la maleta es compatible con la hipótesis nula (esto no garantiza que no haya material radiactivo, solo que no tenemos suficiente evidencia para sugerir que sí). Por otro lado, si la hipótesis nula predice 3 conteos por minuto (para lo cual la distribución de Poisson predice solo un 0,1 % de probabilidad de registrar 10 o más conteos), entonces la maleta no es compatible con la hipótesis nula y es probable que haya otros factores responsables. para producir las medidas.
La prueba no afirma directamente la presencia de material radiactivo. Una prueba exitosa afirma que la afirmación de que no hay material radiactivo presente es poco probable dada la lectura (y por lo tanto...). El doble negativo (refutar la hipótesis nula) del método es confuso, pero usar un contraejemplo para refutar es una práctica matemática estándar. El atractivo del método es su practicidad. Conocemos (por experiencia) el rango esperado de recuentos solo con la presencia de radiactividad ambiental, por lo que podemos decir que una medición es inusualmente grande. La estadística simplemente formaliza lo intuitivo mediante el uso de números en lugar de adjetivos. Probablemente desconozcamos las características de las maletas radiactivas; simplemente asumimos que producen lecturas más grandes.
Para formalizar un poco la intuición: se sospecha radiactividad si el recuento Geiger con la maleta se encuentra entre los mayores (5 % o 1 %) de los recuentos Geiger realizados únicamente con radiación ambiental o los supera. Esto no hace suposiciones sobre la distribución de conteos. Se requieren muchas observaciones de radiación ambiental para obtener buenas estimaciones de probabilidad de eventos raros.
La prueba descrita aquí es más completamente la prueba de significancia estadística de hipótesis nula. La hipótesis nula representa lo que creeríamos por defecto, antes de ver ninguna evidencia. La significación estadística es un posible hallazgo de la prueba, declarado cuando es poco probable que la muestra observada se haya producido por casualidad si la hipótesis nula fuera cierta. El nombre de la prueba describe su formulación y su posible resultado. Una característica de la prueba es su decisión nítida: rechazar o no rechazar la hipótesis nula. Un valor calculado se compara con un umbral, que se determina a partir del riesgo tolerable de error.
Variaciones y subclases
La prueba de hipótesis estadística es una técnica clave tanto de la inferencia frecuentista como de la inferencia bayesiana, aunque los dos tipos de inferencia tienen diferencias notables. Las pruebas de hipótesis estadísticas definen un procedimiento que controla (fija) la probabilidad de decidir incorrectamente que una posición predeterminada (hipótesis nula) es incorrecta. El procedimiento se basa en la probabilidad de que ocurra un conjunto de observaciones si la hipótesis nula fuera verdadera. Esta probabilidad de tomar una decisión incorrecta no es la probabilidad de que la hipótesis nula sea verdadera, ni tampoco si alguna hipótesis alternativa específica es verdadera. Esto contrasta con otras técnicas posibles de la teoría de la decisión en las que las hipótesis nula y alternativa se tratan de manera más equitativa.
Un enfoque bayesiano ingenuo para la prueba de hipótesis es basar las decisiones en la probabilidad posterior, pero esto falla cuando se comparan hipótesis puntuales y continuas. Otros enfoques de la toma de decisiones, como la teoría de decisiones bayesiana, intentan equilibrar las consecuencias de las decisiones incorrectas en todas las posibilidades, en lugar de concentrarse en una única hipótesis nula. Se encuentran disponibles varios otros enfoques para tomar una decisión basada en datos a través de la teoría de la decisión y las decisiones óptimas, algunas de las cuales tienen propiedades deseables. Sin embargo, la prueba de hipótesis es un enfoque dominante para el análisis de datos en muchos campos de la ciencia. Las extensiones a la teoría de la prueba de hipótesis incluyen el estudio del poder de las pruebas, es decir, la probabilidad de rechazar correctamente la hipótesis nula dado que es falsa. Estas consideraciones se pueden utilizar para determinar el tamaño de la muestra antes de la recopilación de datos.
Prueba de hipótesis de Neymar-Pearson
Se puede realizar un ejemplo de prueba de hipótesis de Neyman-Pearson (o prueba de significación estadística de hipótesis nula) mediante un cambio en el ejemplo de la maleta radiactiva. Si la "maleta" es en realidad un contenedor blindado para el transporte de material radiactivo, entonces se podría usar una prueba para seleccionar entre tres hipótesis: ninguna fuente radiactiva presente, una presente, dos (todas) presentes. La prueba podría ser requerida por seguridad, con acciones requeridas en cada caso. El lema de Neyman-Pearson de la prueba de hipótesis dice que un buen criterio para la selección de hipótesis es la razón de sus probabilidades (una razón de verosimilitud). Un método simple de solución es seleccionar la hipótesis con la probabilidad más alta para los conteos Geiger observados. El resultado típico coincide con la intuición: pocos recuentos implican ninguna fuente, muchos recuentos implican dos fuentes y recuentos intermedios implican una fuente. Nótese también que por lo general hay problemas para probar una negativa. Las hipótesis nulas deben ser al menos falsables.
La teoría de Neymar-Pearson puede acomodar tanto las probabilidades previas como los costos de las acciones resultantes de las decisiones. El primero permite que cada prueba considere los resultados de pruebas anteriores (a diferencia de las pruebas de significación de Fisher). Este último permite la consideración de cuestiones económicas (por ejemplo) así como de probabilidades. Una razón de verosimilitud sigue siendo un buen criterio para seleccionar entre hipótesis.
Las dos formas de prueba de hipótesis se basan en diferentes formulaciones de problemas. La prueba original es análoga a una pregunta de verdadero/falso; la prueba de Neyman-Pearson es más como una opción múltiple. En opinión de Tukey, el primero produce una conclusión sobre la base únicamente de pruebas sólidas, mientras que el segundo produce una decisión sobre la base de las pruebas disponibles. Si bien las dos pruebas parecen bastante diferentes tanto matemática como filosóficamente, los desarrollos posteriores conducen a la afirmación opuesta. Considere muchas fuentes radiactivas diminutas. Las hipótesis pasan a ser 0,1,2,3... granos de arena radiactiva. Hay poca distinción entre nada o algo de radiación (Fisher) y 0 granos de arena radiactiva frente a todas las alternativas (Neyman-Pearson). El principal artículo de Neyman-Pearson de 1933 también consideró hipótesis compuestas (aquellas cuya distribución incluye un parámetro desconocido). Un ejemplo demostró lo óptimo de la prueba t de (Estudiante), "no puede haber mejor prueba para la hipótesis bajo consideración" (pág. 321). La teoría de Neyman-Pearson estaba demostrando la optimización de los métodos de Fisher desde sus inicios.
La prueba de significación de Fisher ha demostrado ser una herramienta estadística popular y flexible en aplicaciones con poco potencial de crecimiento matemático. La prueba de hipótesis de Neyman-Pearson se afirma como un pilar de las estadísticas matemáticas, creando un nuevo paradigma para el campo. También estimuló nuevas aplicaciones en control estadístico de procesos, teoría de detección, teoría de decisiones y teoría de juegos. Ambas formulaciones han tenido éxito, pero los éxitos han sido de carácter diferente.
La disputa sobre las formulaciones no está resuelta. La ciencia utiliza principalmente la formulación de Fisher (ligeramente modificada) como se enseña en la introducción a la estadística. Los estadísticos estudian la teoría de Neyman-Pearson en la escuela de posgrado. Los matemáticos están orgullosos de unir las formulaciones. Los filósofos los consideran por separado. Las opiniones eruditas consideran que las formulaciones son diversamente competitivas (Fisher vs Neyman), incompatibles o complementarias. La disputa se ha vuelto más compleja desde que la inferencia bayesiana ha alcanzado respetabilidad.
La terminología es inconsistente. La prueba de hipótesis puede significar cualquier mezcla de dos formulaciones que cambiaron con el tiempo. Cualquier discusión sobre la prueba de significación frente a la prueba de hipótesis es doblemente vulnerable a la confusión.
Fisher pensó que la prueba de hipótesis era una estrategia útil para realizar el control de calidad industrial; sin embargo, no estaba de acuerdo con que la prueba de hipótesis pudiera ser útil para los científicos. La prueba de hipótesis proporciona un medio para encontrar las estadísticas de prueba utilizadas en las pruebas de significación. El concepto de potencia es útil para explicar las consecuencias de ajustar el nivel de significación y se usa mucho en la determinación del tamaño de la muestra. Los dos métodos siguen siendo filosóficamente distintos. Generalmente (pero no siempre) producen la misma respuesta matemática. La respuesta preferida depende del contexto. Si bien la fusión existente de las teorías de Fisher y Neyman-Pearson ha sido fuertemente criticada, se ha considerado modificar la fusión para lograr los objetivos bayesianos.
Crítica
Las críticas a las pruebas de hipótesis estadísticas llenan volúmenes. Gran parte de las críticas se pueden resumir en los siguientes temas:
- La interpretación de una p- el valor depende de detener la regla y la definición de comparación múltiple. El primero a menudo cambia durante el curso de un estudio y éste es inevitablemente ambiguo. (es decir, "los valores de p dependen tanto de los (datos) observados como del otro posible (datos) que podrían haber sido observados pero no fueron").
- Confusión resultante (en parte) de combinar los métodos de Fisher y Neyman-Pearson que son conceptualmente distintos.
- Se hace hincapié en la importancia estadística para la exclusión de la estimación y la confirmación por experimentos repetidos.
- Rigidly requiring statistical significance as a criterion for publication, resulting in publication bias. La mayoría de las críticas son indirectas. En lugar de equivocarse, las pruebas de hipótesis estadísticas son malinterpretadas, sobreutilizadas y mal utilizadas.
- Cuando se utiliza para detectar si existe una diferencia entre grupos, surge una paradoja. A medida que se realizan mejoras en el diseño experimental (por ejemplo, mayor precisión de medida y tamaño de muestra), la prueba se vuelve más indulgente. A menos que se acepte la absurda suposición de que todas las fuentes de ruido en los datos cancelan por completo, la posibilidad de encontrar significación estadística en ambas direcciones se aproxima al 100%. Sin embargo, esta absurda suposición de que la diferencia media entre dos grupos no puede ser cero implica que los datos no pueden ser independientes y distribuidos idénticamente (i.i.d.) porque la diferencia esperada entre dos subgrupos de i.i.d. variatos aleatorios es cero; por lo tanto, la suposición i.i.d. también es absurda.
- Capas de preocupaciones filosóficas. La probabilidad de significación estadística es una función de las decisiones adoptadas por los experimentadores/analistas. Si las decisiones se basan en la convención se denominan arbitrarias o insensatas, mientras que las que no se basan pueden considerarse subjetivas. Para minimizar los errores del tipo II, se recomiendan muestras grandes. En la psicología prácticamente todas las hipótesis nulas se afirman falsas para muestras suficientemente grandes así que "... generalmente no es sensible para realizar un experimento con el sole objetivo de rechazar la hipótesis nula." "Los resultados estadísticamente significativos son a menudo engañosos" en la psicología. La significación estadística no implica significado práctico, y la correlación no implica causación. Poner en duda la hipótesis nula está lejos de apoyar directamente la hipótesis de investigación.
- "No nos dice lo que queremos saber". Existen listas de docenas de denuncias.
Críticos y partidarios están en gran medida de acuerdo con respecto a las características de la prueba de significación de hipótesis nula (NHST): si bien puede proporcionar información crítica, es inadecuada como única herramienta para el análisis estadístico. Rechazar con éxito la hipótesis nula puede no ofrecer apoyo para la hipótesis de la investigación. La controversia continua se refiere a la selección de las mejores prácticas estadísticas para el futuro a corto plazo dadas las prácticas existentes. Sin embargo, un diseño de investigación adecuado puede minimizar este problema. Los críticos preferirían prohibir NHST por completo, forzando una salida completa de esas prácticas, mientras que los partidarios sugieren un cambio menos absoluto.
La controversia sobre las pruebas de significancia y sus efectos sobre el sesgo de publicación en particular ha producido varios resultados. La Asociación Estadounidense de Psicología ha fortalecido sus requisitos de informes estadísticos después de la revisión, los editores de revistas médicas han reconocido la obligación de publicar algunos resultados que no son estadísticamente significativos para combatir el sesgo de publicación y una revista (Journal of Articles in Support of the Null Hypothesis< /i>) ha sido creado para publicar dichos resultados exclusivamente. Los libros de texto han agregado algunas precauciones y han aumentado la cobertura de las herramientas necesarias para estimar el tamaño de la muestra requerida para producir resultados significativos. Las principales organizaciones no han abandonado el uso de pruebas de significación, aunque algunas han discutido hacerlo.
Alternativas
Una posición unificadora de los críticos es que las estadísticas no deben conducir a una conclusión o decisión de aceptación o rechazo, sino a un valor estimado con una estimación de intervalo; esta filosofía de análisis de datos se conoce ampliamente como estadística de estimación. Las estadísticas de estimación se pueden lograr con métodos frecuentistas [1] o bayesianos.
Un fuerte crítico de las pruebas de significancia sugirió una lista de alternativas de informes: tamaños de efecto para importancia, intervalos de predicción para confianza, replicaciones y extensiones para replicabilidad, metanálisis para generalidad. Ninguna de estas alternativas sugeridas produce una conclusión/decisión. Lehmann dijo que la teoría de la prueba de hipótesis se puede presentar en términos de conclusiones/decisiones, probabilidades o intervalos de confianza. "La distinción entre los... enfoques es en gran parte una de información e interpretación."
En una "alternativa" no hay desacuerdo: el propio Fisher dijo: "En relación con la prueba de significancia, podemos decir que un fenómeno es experimentalmente demostrable cuando sabemos cómo realizar un experimento que rara vez fallará en darnos un resultado estadísticamente significativo". " Cohen, un crítico influyente de las pruebas de significación, estuvo de acuerdo: "... no busque una alternativa mágica a NHST [prueba de significación de hipótesis nula]... No lo hace".;t existe." "... dados los problemas de la inducción estadística, finalmente debemos confiar, como lo han hecho las ciencias más antiguas, en la replicación." La "alternativa" a la prueba de significación se repite la prueba. La forma más fácil de disminuir la incertidumbre estadística es obtener más datos, ya sea aumentando el tamaño de la muestra o repitiendo las pruebas. Nickerson afirmó no haber visto nunca la publicación de un experimento de psicología reproducido literalmente. Un enfoque indirecto para la replicación es el metanálisis.
La inferencia bayesiana es una alternativa propuesta a las pruebas de significación. (Nickerson citó 10 fuentes que lo sugieren, incluida Rozeboom (1960)). Por ejemplo, la estimación de parámetros bayesianos puede proporcionar información valiosa sobre los datos a partir de los cuales los investigadores pueden hacer inferencias, al tiempo que utilizan datos previos inciertos que ejercen solo una influencia mínima en los resultados cuando hay suficientes datos disponibles. El psicólogo John K. Kruschke ha sugerido la estimación bayesiana como una alternativa para la prueba t y también ha contrastado la estimación bayesiana para evaluar valores nulos con la comparación del modelo bayesiano para la prueba de hipótesis. Se pueden comparar dos modelos/hipótesis en competencia utilizando factores de Bayes. Los métodos bayesianos podrían ser criticados por requerir información que rara vez está disponible en los casos en los que se utilizan más las pruebas de significancia. Ni las probabilidades previas ni la distribución de probabilidad del estadístico de prueba bajo la hipótesis alternativa a menudo están disponibles en las ciencias sociales.
Los defensores del enfoque bayesiano a veces afirman que el objetivo de un investigador suele ser evaluar objetivamente la probabilidad de que una hipótesis sea cierta en función de los datos que han recopilado. Ni la prueba de significación de Fisher ni la prueba de hipótesis de Neyman-Pearson pueden proporcionar esta información y no pretenden hacerlo. La probabilidad de que una hipótesis sea verdadera solo puede derivarse del uso de Bayes' Teorema, que no fue satisfactorio tanto para el campo de Fisher como para el de Neyman-Pearson debido al uso explícito de la subjetividad en forma de probabilidad previa. La estrategia de Fisher es eludir esto con el valor p (un índice objetivo basado solo en los datos) seguido de inferencia inductiva, mientras que Neyman-Pearson ideó su enfoque del comportamiento inductivo.
Contenido relacionado
Ley de Little
Demografía de Dinamarca
Demografía de Yemen