Proyección estereográfica

Ajustar Compartir Imprimir Citar

Cartografía particular que proyecta una esfera en un plano

ilustración 3D de una proyección estereográfica desde el polo norte en un plano debajo de la esfera

En matemáticas, una proyección estereográfica es una proyección en perspectiva de la esfera, a través de un punto específico de la esfera (el polo o centro de proyección), sobre un plano (el plano de proyección) perpendicular al diámetro a través del punto. Es una función biyectiva suave de toda la esfera excepto el centro de proyección a todo el plano. Asigna círculos en la esfera a círculos o líneas en el plano, y es conforme, lo que significa que conserva los ángulos en los que se encuentran las curvas y, por lo tanto, conserva las formas localmente de forma aproximada. No es ni isométrica (preservación de la distancia) ni equiárea (preservación del área).

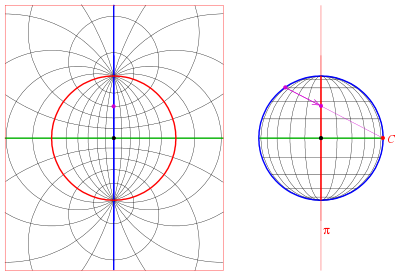
La proyección estereográfica da una forma de representar una esfera por un plano. La métrica inducida por la proyección estereográfica inversa del plano a la esfera define una distancia geodésica entre puntos del plano igual a la distancia esférica entre los puntos esféricos que representan. Un sistema de coordenadas bidimensional en el plano estereográfico es una configuración alternativa para la geometría analítica esférica en lugar de coordenadas polares esféricas o coordenadas cartesianas tridimensionales. Este es el análogo esférico del modelo de disco de Poincaré del plano hiperbólico.

Intuitivamente, la proyección estereográfica es una forma de representar la esfera como el plano, con algunos compromisos inevitables. Debido a que la esfera y el plano aparecen en muchas áreas de las matemáticas y sus aplicaciones, también lo hace la proyección estereográfica; encuentra uso en diversos campos, incluidos el análisis complejo, la cartografía, la geología y la fotografía. A veces, los cálculos estereográficos se realizan gráficamente utilizando un tipo especial de papel cuadriculado llamado red estereográfica, abreviado como stereonet, o red de Wulff.

Historia

Ilustración de Rubens por "Opticorum libri sex philosophis juxta ac mathematicis utiles", de François d'Aguilon. Muestra el principio de una proyección general de la perspectiva, de la cual la proyección estereográfica es un caso especial.

La proyección estereográfica fue conocida por Hiparco, Ptolomeo y probablemente antes por los egipcios. Originalmente se conocía como la proyección del planisferio. Planisphaerium de Ptolomeo es el documento sobreviviente más antiguo que lo describe. Uno de sus usos más importantes fue la representación de cartas celestes. El término planisferio todavía se usa para referirse a tales cartas.

En los siglos XVI y XVII, el aspecto ecuatorial de la proyección estereográfica se usaba comúnmente para los mapas de los hemisferios oriental y occidental. Se cree que el mapa creado en 1507 por Gualterius Lud ya estaba en proyección estereográfica, al igual que más tarde los mapas de Jean Roze (1542), Rumold Mercator (1595) y muchos otros. En las cartas estelares, incluso este aspecto ecuatorial ya había sido utilizado por los antiguos astrónomos como Ptolomeo.

François d'Aguilon le dio a la proyección estereográfica su nombre actual en su obra de 1613 Opticorum libri sex philosophis juxta ac mathematicis utiles (Seis libros de óptica, útiles tanto para filósofos como para matemáticos).

A finales del siglo XVI, Thomas Harriot demostró que la proyección estereográfica es conforme; sin embargo, esta prueba nunca se publicó y permaneció entre sus papeles en una caja durante más de tres siglos. En 1695, Edmond Halley, motivado por su interés por las cartas estelares, fue el primero en publicar una demostración. Usó las herramientas de cálculo recientemente establecidas, inventadas por su amigo Isaac Newton.

Definición

Primera formulación

Proyección estereográfica de la esfera de unidad desde el polo norte hasta el plano

z = 0

, se muestra aquí en la sección transversal

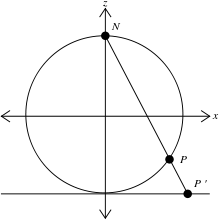
La esfera unitaria $S 2$ en el espacio tridimensional $R 3$ es el conjunto de puntos $(x, y, z)$ tal que $x 2 + y 2 + z 2 = 1$ . Sea $N = (0, 0, 1)$ el "polo norte", y sea M sea el resto de la esfera. El plano $z = 0$ pasa por el centro de la esfera; el "ecuador" es la intersección de la esfera con este plano.

Para cualquier punto $P$ en M, hay una única línea a través de $N$ y $P$ , y esta recta corta al plano $z = 0$ en exactamente un punto $P'$ , conocida como la proyección estereográfica de $P$ en el avión.

En coordenadas cartesianas $(x, y, z)$ en la esfera y $(X, Y)$ en el plano, la proyección y su inversa están dadas por las fórmulas

{displaystyle {begin{aligned}(X,Y)&=left({frac {x}{1-z}},{frac {y}{1-z}}right),\(x,y,z)&=left({frac {2X}{1+X^{2}+Y^{2}}},{frac {2Y}{1+X^{2}+Y^{2}}},{frac {-1+X^{2}+Y^{2}}{1+X^{2}+Y^{2}}}right).end{aligned}}}

En coordenadas esféricas $(φ, θ)$ en la esfera (con $φ$ el ángulo cenital, $0 \leq φ \leq π$ y $θ$ el acimut, $0 \leq θ \leq 2π$ ) y coordenadas polares $(R, Θ)$ en el plano, la proyección y su inversa son

{displaystyle {begin{aligned}(R,Theta)&=left({frac {sin varphi }{1-cos varphi }},theta right)=left(cot {frac {varphi }{2}},theta right),\(varphitheta)&=left(2arctan {frac {1}{R}},Theta right).end{aligned}}}

Aquí, se entiende que $φ$ tiene un valor $π$ cuando $R$ = 0. Además, hay muchas maneras de reescribir estas fórmulas usando identidades trigonométricas. En coordenadas cilíndricas $(r, θ, z)$ en la esfera y coordenadas polares $(R, Θ)$ en el plano, la proyección y su inversa son

{displaystyle {begin{aligned}(R,Theta)&=left({frac {r}{1-z}},theta right),\(r,thetaz)&=left({frac {2R}{1+R^{2}}},Theta{frac {R^{2}-1}{R^{2}+1}}right).end{aligned}}}

Otras convenciones

Proyección estereográfica de la esfera de unidad desde el polo norte hasta el plano

z = 1 -

, se muestra aquí en la sección transversal

Algunos autores definen la proyección estereográfica desde el polo norte (0, 0, 1) sobre el plano $z = -1$ , que es tangente a la esfera unitaria en el polo sur (0, 0, −1). Los valores $X$ y $Y$ producidos por esta proyección son exactamente el doble los producidos por la proyección ecuatorial descrita en el apartado anterior. Por ejemplo, esta proyección envía el ecuador al círculo de radio 2 centrado en el origen. Mientras que la proyección ecuatorial no produce distorsión de área infinitesimal a lo largo del ecuador, esta proyección polo-tangente en cambio no produce distorsión de área infinitesimal en el polo sur.

Otros autores usan una esfera de radio $1 / 2$ y el avión $z = - 1 / 2$ . En este caso las fórmulas se convierten en

{displaystyle {begin{aligned}(x,y,z)rightarrow (xieta)&=left({frac {x}{{frac {1}{2}}-z}},{frac {y}{{frac {1}{2}}-z}}right),\(xieta)rightarrow (x,y,z)&=left({frac {xi }{1+xi ^{2}+eta ^{2}}},{frac {eta }{1+xi ^{2}+eta ^{2}}},{frac {-1+xi ^{2}+eta ^{2}}{2+2xi ^{2}+2eta ^{2}}}right).end{aligned}}}

Proyección estereográfica de una esfera desde un punto

Q

en el avión

E

, se muestra aquí en la sección transversal

En general, se puede definir una proyección estereográfica desde cualquier punto $Q$ de la esfera hacia cualquier plano $E$ tal que

$E$ es perpendicular al diámetro a través $Q$ , y
$E$ no contiene $Q$ .

Siempre que $E$ cumpla con estas condiciones, entonces para cualquier punto $P$ que no sea $Q$ la línea a través de $P$ y $Q$ se encuentra con $E$ exactamente en un punto $P'$ , que se define como la proyección estereográfica de P sobre E.

Generalizaciones

De manera más general, la proyección estereográfica se puede aplicar a la unidad n-esfera $S n$ en ( $n + 1$ ) espacio euclidiano dimensional $E n +1$ . Si $Q$ es un punto de $S n$ y $E$ un hiperplano en $E n +1$ , entonces la proyección estereográfica de un punto $P \in S n - {Q}$ es el punto $P'$ de intersección de la línea $QP$ con $E$ . En coordenadas cartesianas ( $x i$ , $i$ de 0 a $n$ ) en $S n$ y ( $X i$ , $i$ de 1 a n) en $E$ , la proyección de $Q = (1, 0, 0,..., 0) \in S n$ viene dado por

{displaystyle X_{i}={frac {x_{i}}{1-x_{0}}}quad (i=1,dotsn).}

{displaystyle s^{2}=sum _{j=1}^{n}X_{j}^{2}={frac {1+x_{0}}{1-x_{0}}},}

{displaystyle x_{0}={frac {s^{2}-1}{s^{2}+1}}quad {text{and}}quad x_{i}={frac {2X_{i}}{s^{2}+1}}quad (i=1,dotsn).}

Aún de manera más general, suponga que $S$ es una hipersuperficie cuádrica (no singular) en el espacio proyectivo $P n +1$ . En otras palabras, $S$ es el lugar geométrico de los ceros de una forma cuadrática no singular $f (x 0,..., x n +1)$ en las coordenadas homogéneas $x i$ . Fija cualquier punto $Q$ en $S$ y un hiperplano $E$ en $P n +1$ que no contiene $Q$ . Entonces la proyección estereográfica de un punto $P$ en $S - {Q}$ es el único punto de intersección de $QP$ con $E$ . Como antes, la proyección estereográfica es conforme e invertible fuera de un "pequeño" colocar. La proyección estereográfica presenta la hipersuperficie cuádrica como una hipersuperficie racional. Esta construcción juega un papel en la geometría algebraica y la geometría conforme.

Propiedades

La primera proyección estereográfica definida en la sección anterior envía el "polo sur" (0, 0, −1) de la esfera unitaria a (0, 0), el ecuador al círculo unitario, el hemisferio sur a la región dentro del círculo y el hemisferio norte a la región fuera del círculo.

La proyección no está definida en el punto de proyección $N$ = (0, 0, 1). Las pequeñas vecindades de este punto se envían a subconjuntos del plano alejados de (0, 0). Cuanto más cerca está $P$ de (0, 0, 1), más distante está su imagen de (0, 0) en el plano. Por esta razón, es común hablar de (0, 0, 1) como mapeo a "infinito" en el plano, y de la esfera como completando el plano añadiendo un punto en el infinito. Esta noción encuentra utilidad en geometría proyectiva y análisis complejo. En un nivel meramente topológico, ilustra cómo la esfera es homeomorfa a la compactación en un punto del plano.

En coordenadas cartesianas un punto $P (x, y, z)$ sobre la esfera y su imagen $P' (X, Y)$ en el plano o ambos son puntos racionales o ninguno de ellos:

{displaystyle Pin mathbb {Q} ^{3}iff P'in mathbb {Q} ^{2}}

Una rejilla cartesiana en el plano parece distorsionada en la esfera. Las líneas de rejilla siguen siendo perpendiculares, pero las áreas de las cuadrículas se encogen cuando se acercan al polo norte.

Una red polar en el plano parece distorsionada en la esfera. Las curvas de rejilla siguen siendo perpendiculares, pero las áreas de los sectores de rejilla se reducen a medida que se acercan al polo norte.

La proyección estereográfica es conforme, lo que significa que conserva los ángulos en los que las curvas se cruzan entre sí (ver figuras). Por otro lado, la proyección estereográfica no preserva el área; en general, el área de una región de la esfera no es igual al área de su proyección sobre el plano. El elemento de área se proporciona en coordenadas $(X, Y)$ por

dA = frac{4}{(1 + X^2 + Y^2)^2} ; dX ; dY.

A lo largo del círculo unitario, donde $X 2 + Y 2 = 1$ , no hay inflación del área en el límite, lo que da un factor de escala de 1. Las áreas cercanas a (0, 0) se inflan con un factor de 4, y las áreas cercanas al infinito se inflan con factores arbitrariamente pequeños.

La métrica se proporciona en coordenadas $(X, Y)$ por

frac{4}{(1 + X^2 + Y^2)^2} ; (dX^2 + dY^2),

y es la fórmula única que se encuentra en Habilitationsschrift de Bernhard Riemann sobre los fundamentos de la geometría, entregado en Göttingen en 1854, y titulado Über die Hypothesen welche der Geometrie zu Grunde liegen .

Ningún mapa de la esfera al plano puede ser tanto conforme como conservador del área. Si lo fuera, sería una isometría local y conservaría la curvatura gaussiana. La esfera y el plano tienen diferentes curvaturas gaussianas, por lo que esto es imposible.

Círculos en la esfera que hacen no pasar por el punto de proyección se proyectan a círculos en el avión. Círculos en la esfera que do pasar por el punto de proyección se proyectan a líneas rectas en el plano. Estas líneas se consideran a veces como círculos a través del punto en el infinito, o círculos de radio infinito. Estas propiedades se pueden verificar utilizando las expresiones de $x,y,z$ en términos de ${displaystyle X,Y,Z,}$ dada en § Primera formulación: usando estas expresiones para una sustitución en la ecuación ${displaystyle ax+by+cz-d=0}$ del plano que contiene un círculo en la esfera, y los denominadores que aclaran, se obtiene la ecuación de un círculo, es decir, una ecuación de segundo grado con ${displaystyle (c-d)(X^{2}+Y^{2})}$ como su parte cuadrática. La ecuación se vuelve lineal si ${displaystyle c=d,}$ es decir, si el avión pasa por el punto de proyección.

Todas las líneas en el plano, cuando se transforman en círculos en la esfera por el inverso de la proyección estereográfica, se encuentran en el punto de proyección. Las líneas paralelas, que no se cortan en el plano, se transforman en círculos tangentes en el punto de proyección. Las líneas que se intersecan se transforman en círculos que se intersecan transversalmente en dos puntos de la esfera, uno de los cuales es el punto de proyección. (Observaciones similares valen para el plano proyectivo real, pero las relaciones de intersección son diferentes allí).

La esfera, con varios loxodromas mostrados en colores distintos

Las loxódromos de la esfera corresponden a curvas en el plano de la forma

{displaystyle R=e^{Theta /a},,}

donde el parámetro $a$ mide la "estanqueidad" de la loxódromo. Así, las loxódromos corresponden a espirales logarítmicas. Estas espirales intersecan líneas radiales en el plano en ángulos iguales, al igual que las loxódromos intersecan meridianos en la esfera en ángulos iguales.

La proyección estereográfica se relaciona con la inversión del plano de forma sencilla. Sean $P$ y $Q$ dos puntos en la esfera con proyecciones $P'$ y $Q'$ en el avión. Luego $P'$ y $Q'$ son imágenes invertidas entre sí en la imagen de el círculo ecuatorial si y solo si $P$ y $Q$ son reflejos uno del otro en el plano ecuatorial.

En otras palabras, si:

$P$ es un punto en la esfera, pero no un polo norte ' $N$ y no su antipodo, el poste del sur ' $S$ ,
$P .$ es la imagen de $P$ en una proyección estereográfica con el punto de proyección $N$ y
$P'$ es la imagen de $P$ en una proyección estereográfica con el punto de proyección $S$ ,

entonces $P'$ y $P″$ son imágenes inversas entre sí en el círculo unitario.

triangle NOP^prime sim triangle P^{primeprime}OS implies OP^prime:ON = OS: OP^{primeprime} implies OP^prime cdot OP^{primeprime} = r^2

Red Wulff

Wulff net o estéreonet, utilizado para hacer parcelas de la proyección estereográfica a mano

La generación de una red Wulff (red circular dentro del círculo rojo) por una proyección estereográfica con centro C y plano de proyección

pi

Las gráficas de proyección estereográfica pueden ser realizadas por una computadora usando las fórmulas explícitas dadas arriba. Sin embargo, para graficar a mano estas fórmulas son difíciles de manejar. En cambio, es común usar papel cuadriculado diseñado específicamente para la tarea. Este papel cuadriculado especial se llama estereonet o red de Wulff, en honor al mineralogista ruso George (Yuri Viktorovich) Wulff.

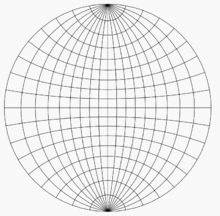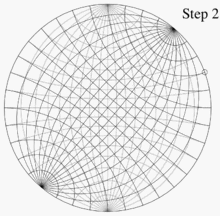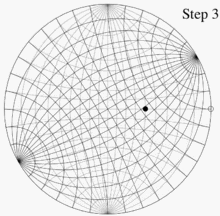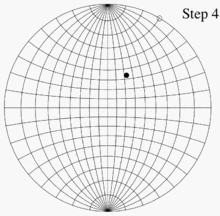
La red de Wulff que se muestra aquí es la proyección estereográfica de la cuadrícula de paralelos y meridianos de un hemisferio centrado en un punto del ecuador (como el hemisferio oriental u occidental de un planeta).

En la figura, la propiedad de distorsión de área de la proyección estereográfica se puede ver comparando un sector de cuadrícula cerca del centro de la red con uno en el extremo derecho o izquierdo. Los dos sectores tienen áreas iguales en la esfera. En el disco, este último tiene casi cuatro veces el área del primero. Si la cuadrícula se hace más fina, esta relación se aproxima exactamente a 4.

En la red de Wulff, las imágenes de los paralelos y los meridianos se cruzan en ángulo recto. Esta propiedad de ortogonalidad es consecuencia de la propiedad de conservación del ángulo de la proyección estereográfica. (Sin embargo, la propiedad de conservación del ángulo es más fuerte que esta propiedad. No todas las proyecciones que conservan la ortogonalidad de los paralelos y meridianos conservan el ángulo).

Ilustración de los pasos 1-4 para trazar un punto en una red Wulff

Para ver un ejemplo del uso de la red de Wulff, imagina dos copias en papel delgado, una encima de la otra, alineadas y unidas en su centro mutuo. Sea $P$ el punto en el hemisferio unitario inferior cuyas coordenadas esféricas son (140°, 60°) y cuyas coordenadas cartesianas son (0.321, 0.557, −0,766). Este punto se encuentra en una línea orientada 60° en sentido antihorario desde el eje positivo $x$ (o 30° en el sentido de las agujas del reloj desde el eje positivo $y$ ) y 50° por debajo del plano horizontal $z = 0$ . Una vez que se conocen estos ángulos, hay cuatro pasos para trazar $P$ :

Usando las líneas de rejilla, que están separadas 10° en las figuras aquí, marque el punto en el borde de la red que es 60° en sentido contrario desde el punto (1, 0) (o 30° en sentido del reloj desde el punto (0, 1)).
Gira la red superior hasta que este punto esté alineado con (1, 0) en la red inferior.
Usando las líneas de rejilla en la red inferior, marque el punto que es 50° hacia el centro desde ese punto.
Girar la red superior opuestamente a cómo se orientó antes, para traerla de nuevo en alineación con la red inferior. El punto marcado en el paso 3 es entonces la proyección que queríamos.

Para trazar otros puntos, cuyos ángulos no son números redondos como 60° y 50°, uno debe interpolar visualmente entre las líneas de cuadrícula más cercanas. Es útil tener una red con un espacio menor a 10°. Los espaciamientos de 2° son comunes.

Para encontrar el ángulo central entre dos puntos de la esfera en función de su gráfico estereográfico, superponga el gráfico en una red de Wulff y gire el gráfico sobre el centro hasta que los dos puntos se encuentren en un meridiano o cerca de él. Luego mida el ángulo entre ellos contando las líneas de cuadrícula a lo largo de ese meridiano.

Dos puntos $P 1$ y $P 2$ se dibujan sobre una hoja transparente tacked en el origen de una red Wulff.
La hoja transparente está rota y el ángulo central se lee a lo largo del meridiano común a ambos puntos $P 1$ y $P 2$ .

Aplicaciones dentro de las matemáticas

Análisis complejo

La proyección estereográfica desde el polo norte de una esfera hasta su plano ecuatorial establece una correspondencia entre la esfera y el plano ecuatorial extendido con un punto en el infinito denotado

JUEGO

. Cuando el plano ecuatorial es el plano complejo, esto proporciona una visualización de la esfera Riemann

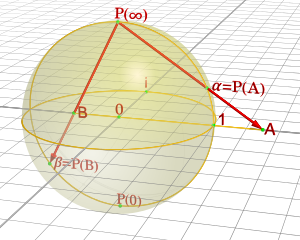
Aunque cualquier proyección estereográfica pierde un punto en la esfera (el punto de proyección), toda la esfera se puede mapear utilizando dos proyecciones desde distintos puntos de proyección. En otras palabras, la esfera puede estar cubierta por dos parametrizaciones estereográficas (las inversas de las proyecciones) desde el plano. Las parametrizaciones se pueden elegir para inducir la misma orientación en la esfera. Juntos, describen la esfera como una superficie orientada (o variedad bidimensional).

Esta construcción tiene un significado especial en el análisis complejo. El punto $(X, Y)$ en el plano real se puede identificar con el número complejo $ζ = X + i Y$ . La proyección estereográfica desde el polo norte sobre el plano ecuatorial es entonces

{displaystyle {begin{aligned}zeta &={frac {x+iy}{1-z}},\\(x,y,z)&=left({frac {2operatorname {Re} zeta }{1+{bar {zeta }}zeta }},{frac {2operatorname {Im} zeta }{1+{bar {zeta }}zeta }},{frac {-1+{bar {zeta }}zeta }{1+{bar {zeta }}zeta }}right).end{aligned}}}

Del mismo modo, siendo $ξ = X - i Y$ otra coordenada compleja, Las funciones

{displaystyle {begin{aligned}xi &={frac {x-iy}{1+z}},\(x,y,z)&=left({frac {2operatorname {Re} xi }{1+{bar {xi }}xi }},{frac {-2operatorname {Im} xi }{1+{bar {xi }}xi }},{frac {1-{bar {xi }}xi }{1+{bar {xi }}xi }}right)end{aligned}}}

define una proyección estereográfica desde el polo sur hacia el plano ecuatorial. Los mapas de transición entre las coordenadas $ζ$ y $ξ$ son entonces $ζ = 1 / ξ$ y $ξ = 1 / ζ$ , con $ζ$ acercándose a 0 como $ξ$ tiende a infinito, y viceversa. Esto facilita una noción elegante y útil del infinito para los números complejos y, de hecho, una teoría completa de las funciones meromórficas que se asignan a la esfera de Riemann. La métrica estándar en la esfera unitaria concuerda con la métrica de Fubini-Study en la esfera de Riemann.

Visualización de líneas y planos

Animación de las líneas Kikuchi de cuatro de las ocho zonas de ocho <111 con un cristal fcc. Los planos se intersectan en ángulos fijos.

El conjunto de todas las líneas que pasan por el origen en el espacio tridimensional forma un espacio llamado plano proyectivo real. Este plano es difícil de visualizar porque no se puede incrustar en un espacio tridimensional.

Sin embargo, uno puede visualizarlo como un disco, de la siguiente manera. Cualquier línea a través del origen intersecta el hemisferio sur $z$ ≤ 0 en un punto, que luego se puede proyectar estereográficamente a un punto en un disco en el XY avión. Las líneas horizontales que pasan por el origen intersecan el hemisferio sur en dos puntos antípodas a lo largo del ecuador, que se proyectan hasta el límite del disco. Cualquiera de los dos puntos proyectados puede considerarse parte del disco; se entiende que los puntos antípodas en el ecuador representan una sola línea en el espacio 3 y un solo punto en el límite del disco proyectado (ver topología del cociente). Entonces, cualquier conjunto de líneas a través del origen puede representarse como un conjunto de puntos en el disco proyectado. Pero los puntos límite se comportan de manera diferente a los puntos límite de un disco bidimensional ordinario, en que cualquiera de ellos está simultáneamente cerca de puntos interiores en lados opuestos del disco (al igual que dos líneas casi horizontales a través del origen pueden proyectarse a puntos en lados opuestos del disco).

Además, cada plano que pasa por el origen se cruza con la esfera unitaria en un gran círculo, llamado traza del plano. Este círculo se asigna a un círculo bajo proyección estereográfica. Entonces, la proyección nos permite visualizar planos como arcos circulares en el disco. Antes de la disponibilidad de las computadoras, las proyecciones estereográficas con grandes círculos a menudo implicaban dibujar arcos de gran radio que requerían el uso de una brújula de haz. Las computadoras ahora hacen esta tarea mucho más fácil.

Además, asociada con cada plano hay una línea única, llamada polo del plano, que pasa por el origen y es perpendicular al plano. Esta línea se puede trazar como un punto en el disco al igual que cualquier línea que pase por el origen. Entonces, la proyección estereográfica también nos permite visualizar planos como puntos en el disco. Para gráficos que involucran muchos planos, trazar sus polos produce una imagen menos desordenada que trazar sus trazas.

Esta construcción se utiliza para visualizar datos direccionales en cristalografía y geología, como se describe a continuación.

Otra visualización

La proyección estereográfica también se aplica a la visualización de politopos. En un diagrama de Schlegel, un politopo $n$ -dimensional en $R n +1$ se proyecta en una esfera $n$ -dimensional, que luego se proyecta estereográficamente en $R n$ . La reducción de $R n +1$ a $R n$ puede hacer que el politopo sea más fácil de visualizar y comprender.

Geometría aritmética

Los puntos racionales en un círculo corresponden, bajo proyección estereográfica, a los puntos racionales de la línea.

En geometría aritmética elemental, la proyección estereográfica del círculo unitario proporciona un medio para describir todas las ternas pitagóricas primitivas. Específicamente, la proyección estereográfica desde el polo norte (0,1) sobre el eje $x$ proporciona una correspondencia uno a uno entre los puntos de números racionales $(x, y)$ en el círculo unitario (con $y \neq 1$ ) y los puntos racionales del eje $x$ . Si $(m / n, 0)$ es un punto racional en $x$ -eje, entonces su proyección estereográfica inversa es el punto

{displaystyle left({frac {2mn}{m^{2}+n^{2}}},{frac {m^{2}-n^{2}}{m^{2}+n^{2}}}right)}

que da la fórmula de Euclides para un triple pitagórico.

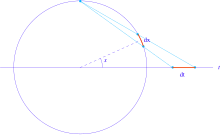
Sustitución de semiángulo tangente

El par de funciones trigonométricas $(sin x, cos x)$ puede considerarse como parametrizar el círculo unitario. La proyección estereográfica da una parametrización alternativa del círculo unitario:

cos x = frac{t^2 - 1}{t^2 + 1},quad sin x = frac{2 t}{t^2 + 1}.

Bajo esta reparametrización, el elemento de longitud $dx$ del círculo unitario pasa a

dx = frac{2 , dt}{t^2 + 1}.

Esta sustitución a veces puede simplificar integrales que involucran funciones trigonométricas.

Aplicaciones a otras disciplinas

Cartografía

El problema fundamental de la cartografía es que ningún mapa de la esfera al plano puede representar con precisión tanto los ángulos como las áreas. En general, las proyecciones cartográficas que preservan el área se prefieren para aplicaciones estadísticas, mientras que las proyecciones cartográficas que preservan el ángulo (conformes) se prefieren para la navegación.

La proyección estereográfica cae en la segunda categoría. Cuando la proyección se centra en el polo norte o sur de la Tierra, tiene propiedades deseables adicionales: envía meridianos a rayos que emanan del origen y paralelos a círculos centrados en el origen.

Proyección estereográfica del mundo norte de 30°S. 15° graticule.
La proyección estereográfica con la indicación de Tissot de la deformación.

Ciencia planetaria

Una proyección estereográfica de la Luna, mostrando regiones hacia los polos de 60° Norte. Los cráteres que son círculos en la esfera aparecen circulares en esta proyección, independientemente de si están cerca del polo o del borde del mapa.

La proyección estereográfica es la única proyección que asigna todos los círculos de una esfera a círculos de un plano. Esta propiedad es valiosa en el mapeo planetario donde los cráteres son características típicas. El conjunto de círculos que pasan por el punto de proyección tienen un radio ilimitado y, por lo tanto, degeneran en líneas.

Cristalografía

Una figura de poste cristalográfica para la rejilla de diamante en [111] dirección

En cristalografía, las orientaciones de los ejes y las caras de los cristales en el espacio tridimensional son una preocupación geométrica central, por ejemplo, en la interpretación de patrones de difracción de rayos X y electrones. Estas orientaciones se pueden visualizar como en la sección Visualización de líneas y planos anterior. Es decir, los ejes y polos de cristal con los planos de cristal se cruzan con el hemisferio norte y luego se trazan mediante proyección estereográfica. Una gráfica de polos se llama figura polar.

En la difracción de electrones, los pares de líneas de Kikuchi aparecen como bandas que decoran la intersección entre las trazas del plano de la red y la esfera de Ewald, proporcionando así acceso experimental a la proyección estereográfica de un cristal. Modele los mapas de Kikuchi en el espacio recíproco y los mapas de visibilidad de franjas para usar con contornos de curvas en el espacio directo, por lo tanto, actúan como mapas de ruta para explorar el espacio de orientación con cristales en el microscopio electrónico de transmisión.

Geología

Uso de la proyección estereográfica hemisférica inferior para trazar datos planos y lineales en geología estructural, utilizando el ejemplo de un plano de falla con una lineación slickenside

Los investigadores en geología estructural se preocupan por las orientaciones de planos y líneas por varias razones. La foliación de una roca es una característica plana que a menudo contiene una característica lineal llamada lineación. De manera similar, un plano de falla es una característica plana que puede contener características lineales como lados de deslizamiento.

Estas orientaciones de líneas y planos en varias escalas se pueden trazar utilizando los métodos de la sección Visualización de líneas y planos anterior. Al igual que en la cristalografía, los planos normalmente se trazan por sus polos. A diferencia de la cristalografía, se utiliza el hemisferio sur en lugar del norte (porque las características geológicas en cuestión se encuentran debajo de la superficie de la Tierra). En este contexto, la proyección estereográfica suele denominarse proyección del hemisferio inferior de ángulos iguales. También se utiliza la proyección del hemisferio inferior de áreas equivalentes definida por la proyección de áreas equivalentes azimutales de Lambert, especialmente cuando el gráfico se va a someter a un análisis estadístico posterior, como el contorno de densidad.

Fotografía

Proyección estereográfica del panorama esférico de la última escultura de la Cena por Michele Vedani en Esino Lario, Lombardía, Italia durante Wikimania 2016

"Vue circulaire des montagnes qu'on découvre du sommet du Glacier de Buet", Horace-Benedict de Saussure, Voyage dans les Alpes, précédés d'un essai sur l'histoire naturelle des environs de Geneve. Neuchatel, 1779–96, pl. 8.

Algunos objetivos de ojo de pez utilizan una proyección estereográfica para capturar una vista de gran angular. En comparación con las lentes de ojo de pez más tradicionales que utilizan una proyección de áreas iguales, las áreas cercanas al borde conservan su forma y las líneas rectas son menos curvas. Sin embargo, las lentes de ojo de pez estereográficas suelen ser más caras de fabricar. El software de reasignación de imágenes, como Panotools, permite la reasignación automática de fotos desde un ojo de pez de áreas iguales a una proyección estereográfica.

La proyección estereográfica se ha utilizado para mapear panoramas esféricos, comenzando con Horace Bénédict de Saussure en 1779. Esto da como resultado efectos conocidos como un pequeño planeta (cuando el centro de proyección es el nadir) y un tubo (cuando el centro de proyección es el cenit).

La popularidad del uso de proyecciones estereográficas para mapear panoramas sobre otras proyecciones azimutales se atribuye a la preservación de la forma que resulta de la conformidad de la proyección.

Te puede interesar
Media armónica
(leer más)
Te puede interesar
Superelipse
(leer más)
Te puede interesar
Elemento de identidad
(leer más)
Más resultados...

Proyección estereográfica

Historia

Definición

Primera formulación

Otras convenciones

Generalizaciones

Propiedades

Red Wulff

Aplicaciones dentro de las matemáticas

Análisis complejo

Visualización de líneas y planos

Otra visualización

Geometría aritmética

Sustitución de semiángulo tangente

Aplicaciones a otras disciplinas

Cartografía

Ciencia planetaria

Cristalografía

Geología

Fotografía

Media armónica

Superelipse

Elemento de identidad