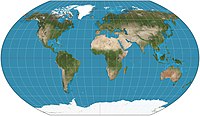
Proyección de mapa
En cartografía, proyección cartográfica es el término utilizado para describir un amplio conjunto de transformaciones empleadas para representar la superficie curva bidimensional de un globo terráqueo en un plano. En una proyección de mapa, las coordenadas, a menudo expresadas como latitud y longitud, de ubicaciones desde la superficie del globo se transforman en coordenadas en un plano. La proyección es un paso necesario en la creación de un mapa bidimensional y es uno de los elementos esenciales de la cartografía.
Todas las proyecciones de una esfera sobre un plano necesariamente distorsionan la superficie de alguna manera y hasta cierto punto. Dependiendo del propósito del mapa, algunas distorsiones son aceptables y otras no; por lo tanto, existen diferentes proyecciones cartográficas para preservar algunas propiedades del cuerpo esférico a expensas de otras propiedades. El estudio de las proyecciones cartográficas trata principalmente de la caracterización de sus distorsiones. No hay límite para el número de posibles proyecciones de mapas. De manera más general, las proyecciones se consideran en varios campos de las matemáticas puras, incluida la geometría diferencial, la geometría proyectiva y las variedades. Sin embargo, el término "proyección de mapa" se refiere específicamente a una proyección cartográfica.
A pesar del significado literal del nombre, la proyección no se limita a las proyecciones en perspectiva, como las que resultan de proyectar una sombra en una pantalla o la imagen rectilínea producida por una cámara estenopeica en una placa de película plana. Más bien, cualquier función matemática que transforme las coordenadas de la superficie curva de manera clara y suave al plano es una proyección. Pocas proyecciones en uso práctico son perspectiva.
La mayor parte de este artículo asume que la superficie a mapear es la de una esfera. La Tierra y otros cuerpos celestes grandes generalmente se modelan mejor como esferoides achatados, mientras que los objetos pequeños como los asteroides suelen tener formas irregulares. Las superficies de los cuerpos planetarios pueden cartografiarse incluso si son demasiado irregulares para modelarse bien con una esfera o un elipsoide. Por lo tanto, de manera más general, una proyección de mapa es cualquier método para aplanar una superficie curva continua en un plano.
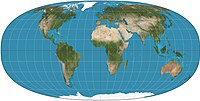
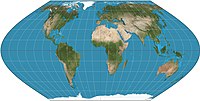
La proyección de mapa más conocida es la proyección de Mercator. Esta proyección cartográfica tiene la propiedad de ser conforme. Sin embargo, ha sido criticado a lo largo del siglo XX por ampliar regiones más alejadas del ecuador. Por el contrario, las proyecciones de áreas iguales, como la proyección sinusoidal y la proyección de Gall-Peters, muestran los tamaños correctos de los países entre sí, pero distorsionan los ángulos. La National Geographic Society y la mayoría de los atlas favorecen las proyecciones de mapas que comprometen el área y la distorsión angular, como la proyección de Robinson y la proyección tripel de Winkel.
Propiedades métricas de los mapas
Muchas propiedades se pueden medir en la superficie de la Tierra independientemente de su geografía:
- Zona
- Forma
- Dirección
- Rodamientos
- Distancia
Se pueden construir proyecciones de mapas para preservar algunas de estas propiedades a expensas de otras. Debido a que la superficie curva de la Tierra no es isométrica a un plano, la preservación de las formas requiere inevitablemente una escala variable y, en consecuencia, una presentación no proporcional de las áreas. De manera similar, una proyección que preserva el área puede no ser conforme, lo que da como resultado formas y rumbos distorsionados en la mayoría de los lugares del mapa. Cada proyección conserva, compromete o aproxima las propiedades métricas básicas de diferentes maneras. El propósito del mapa determina qué proyección debe formar la base del mapa. Debido a que los mapas tienen muchos propósitos diferentes, se ha creado una diversidad de proyecciones para adaptarse a esos propósitos.
Otra consideración en la configuración de una proyección es su compatibilidad con los conjuntos de datos que se utilizarán en el mapa. Los conjuntos de datos son información geográfica; su colección depende del dato (modelo) elegido de la Tierra. Datums diferentes asignan coordenadas ligeramente diferentes a la misma ubicación, por lo que en mapas a gran escala, como los de los sistemas cartográficos nacionales, es importante hacer coincidir el datum con la proyección. Las ligeras diferencias en la asignación de coordenadas entre diferentes datums no son una preocupación para los mapas del mundo o de grandes regiones, donde tales diferencias se reducen a la imperceptibilidad.
Distorsión
El Teorema Egregium de Carl Friedrich Gauss demostró que la superficie de una esfera no se puede representar en un plano sin distorsión. Lo mismo se aplica a otras superficies de referencia utilizadas como modelos para la Tierra, como esferoides achatados, elipsoides y geoides. Dado que cualquier proyección de mapa es una representación de una de esas superficies en un plano, todas las proyecciones de mapa se distorsionan.
La forma clásica de mostrar la distorsión inherente a una proyección es utilizar la indicatriz de Tissot. Para un punto dado, usando el factor de escala h a lo largo del meridiano, el factor de escala k a lo largo del paralelo y el ángulo θ′ entre ellos, Nicolas Tissot describió cómo construir una elipse que ilustra la cantidad y orientación de los componentes de distorsión. Al espaciar las elipses regularmente a lo largo de los meridianos y paralelos, la red de indicatrices muestra cómo varía la distorsión a lo largo del mapa.
Otras métricas de distorsión
Se han descrito muchas otras formas de mostrar la distorsión en las proyecciones. Al igual que la indicatriz de Tissot, la indicatriz de Goldberg-Gott se basa en infinitesimales y representa distorsiones de flexión y sesgo (curvatura y asimetría).
En lugar del círculo infinitesimal original (ampliado) como en la indicatriz de Tissot, algunos métodos visuales proyectan formas finitas que abarcan una parte del mapa. Por ejemplo, un pequeño círculo de radio fijo (por ejemplo, 15 grados de radio angular). A veces se utilizan triángulos esféricos. En la primera mitad del siglo XX, era común proyectar una cabeza humana en diferentes proyecciones para mostrar cómo varía la distorsión en una proyección en comparación con otra. En los medios dinámicos, las formas de las líneas costeras y los límites familiares se pueden arrastrar a través de un mapa interactivo para mostrar cómo la proyección distorsiona los tamaños y las formas según la posición en el mapa.
Otra forma de visualizar la distorsión local es a través de escalas de grises o gradaciones de color cuya sombra representa la magnitud de la deformación angular o la inflación del área. A veces, ambos se muestran simultáneamente al combinar dos colores para crear un mapa bivariado.
Para medir la distorsión globalmente en áreas en lugar de en un solo punto necesariamente implica elegir prioridades para llegar a un compromiso. Algunos esquemas utilizan la distorsión de la distancia como indicador de la combinación de la deformación angular y la inflación del área; tales métodos eligen arbitrariamente qué caminos medir y cómo ponderarlos para producir un único resultado. Muchos han sido descritos.
Diseño y construcción
La creación de una proyección cartográfica consta de dos pasos:
- Selección de un modelo para la forma de la Tierra o cuerpo planetario (usualmente elegir entre una esfera o ellipsoide). Debido a que la forma real de la Tierra es irregular, la información se pierde en este paso.
- Transformación de coordenadas geográficas (longitud y latitud) a Cartesian (x,Sí.) o polar (r, SilencioCoordenadas de avión. En mapas a gran escala, las coordenadas cartesianas normalmente tienen una relación simple con los estentes y los norteños definidos como una cuadrícula superpuesta en la proyección. En los mapas a pequeña escala, los esteros y los norteños no son significativos, y las rejillas no se superponen.
Algunas de las proyecciones cartográficas más sencillas son proyecciones literales, que se obtienen colocando una fuente de luz en algún punto definido relativo al globo y proyectando sus características sobre una superficie específica. Aunque la mayoría de las proyecciones no se definen de esta manera, representar el modelo de fuente de luz-globo puede ser útil para comprender el concepto básico de una proyección cartográfica.
Elegir una superficie de proyección
Una superficie que se puede desplegar o desenrollar en un plano o lámina sin estirarse, rasgarse o encogerse se denomina superficie desarrollable. El cilindro, el cono y el plano son todas superficies desarrollables. La esfera y el elipsoide no tienen superficies desarrollables, por lo que cualquier proyección de ellos sobre un plano tendrá que distorsionar la imagen. (Para comparar, uno no puede aplanar una cáscara de naranja sin rasgarla y deformarla).
Una forma de describir una proyección es primero proyectar desde la superficie de la Tierra a una superficie desarrollable, como un cilindro o un cono, y luego desenrollar la superficie en un plano. Si bien el primer paso distorsiona inevitablemente algunas propiedades del globo, la superficie desarrollable puede luego desplegarse sin más distorsión.
Aspecto de la proyección
Una vez que se elige entre proyectar sobre un cilindro, un cono o un plano, se debe especificar el aspecto de la forma. El aspecto describe cómo se coloca la superficie desarrollable en relación con el globo: puede ser normal (de modo que el eje de simetría de la superficie coincida con el eje de la Tierra), transversa (en ángulo recto con el eje de la Tierra) u oblicua (cualquier ángulo intermedio).
Líneas notables
La superficie desarrollable también puede ser tangente o secante a la esfera o al elipsoide. Tangente significa que la superficie toca pero no corta el globo; secante significa que la superficie corta el globo. Mover la superficie desarrollable lejos del contacto con el globo nunca conserva ni optimiza las propiedades métricas, por lo que esa posibilidad no se discute más aquí.
Las líneas tangente y secante (líneas estándar) se representan sin distorsión. Si estas líneas son un paralelo de latitud, como en las proyecciones cónicas, se llama un paralelo estándar. El meridiano central es el meridiano al que gira el globo antes de proyectarse. El meridiano central (usualmente escrito λ0) y un paralelo de origen (usualmente escrito φ0) son a menudo se utiliza para definir el origen de la proyección cartográfica.
Escala
Un globo es la única forma de representar la Tierra con una escala constante en todo el mapa en todas las direcciones. Un mapa no puede lograr esa propiedad para cualquier área, por pequeña que sea. Sin embargo, puede lograr una escala constante a lo largo de líneas específicas.
Algunas posibles propiedades son:
- La escala depende de la ubicación, pero no de la dirección. Esto equivale a la preservación de ángulos, la característica definitoria de un mapa conformado.
- Escala es constante a lo largo de cualquier paralelo en la dirección del paralelo. Esto se aplica para cualquier proyección cilíndrica o pseudocilíndrica en aspecto normal.
- Combinación de lo anterior: la escala depende sólo de la latitud, no de longitud o dirección. Esto se aplica para la proyección Mercator en aspecto normal.
- Escala es constante a lo largo de todas las líneas rectas que irradian desde una ubicación geográfica particular. Esta es la característica definitoria de una proyección equidistante como la proyección equidistante azimutal. También hay proyecciones (proyección equidistante de dos puntos de Maurer, Close) donde verdaderas distancias de dos. puntos se conservan.
Elegir un modelo por la forma del cuerpo
La construcción de la proyección también se ve afectada por cómo se aproxima la forma de la Tierra o del cuerpo planetario. En la siguiente sección sobre categorías de proyección, la tierra se toma como una esfera para simplificar la discusión. Sin embargo, la forma real de la Tierra está más cerca de un elipsoide achatado. Ya sean esféricos o elipsoidales, los principios discutidos se mantienen sin pérdida de generalidad.
Seleccionar un modelo para una forma de la Tierra implica elegir entre las ventajas y desventajas de una esfera versus un elipsoide. Los modelos esféricos son útiles para mapas a pequeña escala, como atlas mundiales y globos terráqueos, ya que el error a esa escala no suele ser perceptible ni lo suficientemente importante como para justificar el uso del elipsoide más complicado. El modelo elipsoidal se usa comúnmente para construir mapas topográficos y para otros mapas de escala grande y mediana que necesitan representar con precisión la superficie terrestre. A menudo se emplean latitudes auxiliares para proyectar el elipsoide.
Un tercer modelo es el geoide, una representación más compleja y precisa de la forma de la Tierra que coincide con el nivel medio del mar si hubiera no había vientos, mareas o tierra. En comparación con el elipsoide de mejor ajuste, un modelo geoidal cambiaría la caracterización de propiedades importantes como la distancia, la conformidad y la equivalencia. Por lo tanto, en las proyecciones geoidales que preservan tales propiedades, la retícula mapeada se desviaría de la retícula de un elipsoide mapeado. Normalmente, el geoide no se usa como modelo de la Tierra para las proyecciones, sin embargo, porque la forma de la Tierra es muy regular, con una ondulación del geoide que asciende a menos de 100 m del modelo elipsoidal fuera del radio de la Tierra de 6,3 millones de m.. Sin embargo, para cuerpos planetarios irregulares como asteroides, a veces se utilizan modelos análogos al geoide para proyectar mapas.
Otros sólidos regulares a veces se usan como generalizaciones para cuerpos más pequeños' equivalente geoidal. Por ejemplo, Io se modela mejor con un elipsoide triaxial o un esferoide alargado con pequeñas excentricidades. La forma de Haumea es un elipsoide de Jacobi, con su eje mayor dos veces más largo que su menor y con su eje medio una vez y media más largo que su menor. Consulte la proyección del mapa del elipsoide triaxial para obtener más información.
Clasificación
Una forma de clasificar las proyecciones de mapas se basa en el tipo de superficie sobre la que se proyecta el globo. En este esquema, el proceso de proyección se describe como la colocación de una superficie de proyección hipotética del tamaño del área de estudio deseada en contacto con una parte de la Tierra, la transferencia de características de la superficie de la Tierra a la superficie de proyección, y luego el desenredado y escalado de la superficie de proyección en una mapa plano. Las superficies de proyección más comunes son cilíndricas (p. ej., Mercator), cónicas (p. ej., Albers) y planas (p. ej., estereográficas). Sin embargo, muchas proyecciones matemáticas no encajan perfectamente en ninguno de estos tres métodos de proyección. Por lo tanto, se han descrito otras categorías de pares en la literatura, como pseudocónico, pseudocilíndrico, pseudoazimutal, retroazimutal y policónico.
Otra forma de clasificar las proyecciones es según las propiedades del modelo que conservan. Algunas de las categorías más comunes son:
- Dirección de conservación ()azimuthal o zenithal), un rasgo posible sólo de uno o dos puntos a cada otro punto
- Preservar la forma localmente (conformal o ortomorfo)
- Área de conservación (igualdad de zonas o equiareal o equivalente o authalic)
- Guardar distancia (equidistante), un rasgo posible sólo entre uno o dos puntos y cada otro punto
- Preservando la ruta más corta, un rasgo preservado sólo por la proyección gnomónica
Debido a que la esfera no es una superficie desarrollable, es imposible construir una proyección de mapa que sea tanto de áreas iguales como conforme.
Proyecciones por superficie
Las tres superficies desarrollables (plano, cilindro, cono) proporcionan modelos útiles para comprender, describir y desarrollar proyecciones cartográficas. Sin embargo, estos modelos están limitados de dos maneras fundamentales. Por un lado, la mayoría de las proyecciones mundiales en uso no entran en ninguna de esas categorías. Por otro lado, incluso la mayoría de las proyecciones que caen dentro de esas categorías no se pueden lograr naturalmente a través de la proyección física. Como señala L. P. Lee,
No se ha hecho referencia en las definiciones anteriores a cilindros, conos o aviones. Las proyecciones se denominan cilíndricas o cónicas porque se pueden considerar desarrolladas en un cilindro o un cono, como puede ser el caso, pero también es para dispensar con cilindros y conos pictóricos, ya que han dado lugar a mucho malentendido. Particularmente esto es así con respecto a las proyecciones conicas con dos paralelos estándar: pueden ser considerados como desarrollados en conos, pero son conos que no tienen una relación simple con la esfera. En realidad, los cilindros y los conos nos proporcionan términos convenientes descriptivos, pero poco más.
La objeción de Lee se refiere a la forma en que los términos cilíndrico, cónico y planar (azimutal) se han abstracto en el campo de proyecciones cartográficas. Si los mapas se proyectaran como la luz que brilla a través de un globo sobre una superficie desarrollable, entonces el espaciado de los paralelos seguiría un conjunto muy limitado de posibilidades. Tal proyección cilíndrica (por ejemplo) es aquella que:
- Es rectangular;
- Tiene meridianos verticales rectos, espaciados uniformemente;
- Tiene paralelos rectos simétricos sobre el ecuador;
- Ha paralelos limitados a donde caen cuando la luz brilla a través del globo sobre el cilindro, con la fuente de luz en algún lugar a lo largo de la línea formada por la intersección del meridiano primario con el Ecuador, y el centro de la esfera.
(Si gira el globo antes de proyectar, los paralelos y los meridianos no seguirán siendo necesariamente líneas rectas. Normalmente, las rotaciones se ignoran con fines de clasificación).
El lugar donde emana la fuente de luz a lo largo de la línea descrita en esta última restricción es lo que produce las diferencias entre los distintos "naturales" proyecciones cilíndricas. Pero el término cilíndrico como se usa en el campo de las proyecciones cartográficas relaja la última restricción por completo. En cambio, los paralelos se pueden colocar de acuerdo con cualquier algoritmo que el diseñador haya decidido que se adapte a las necesidades del mapa. La famosa proyección de Mercator es aquella en la que la colocación de paralelas no surge por proyección; en cambio, los paralelos se colocan como deben estar para satisfacer la propiedad de que un curso de rumbo constante siempre se traza como una línea recta.
Cilíndrica
(feminine)Cilíndricos normales
Una proyección cilíndrica normal es cualquier proyección en la que los meridianos se asignan a líneas verticales igualmente espaciadas y los círculos de latitud (paralelos) se asignan a líneas horizontales.
La asignación de meridianos a líneas verticales se puede visualizar imaginando un cilindro cuyo eje coincide con el eje de rotación de la Tierra. Este cilindro se envuelve alrededor de la Tierra, se proyecta y luego se desenrolla.
Por la geometría de su construcción, las proyecciones cilíndricas estiran distancias de este a oeste. La cantidad de estiramiento es la misma en cualquier latitud elegida en todas las proyecciones cilíndricas y viene dada por la secante de la latitud como un múltiplo de la escala del ecuador. Las diversas proyecciones cilíndricas se distinguen entre sí únicamente por su extensión norte-sur (donde la latitud viene dada por φ):
- El estiramiento norte-sur equivale al estiramiento este-oeste (sec φ): La escala este-oeste coincide con la escala norte-sur: cilíndrica conformal o Mercator; esto distorsiona las áreas excesivamente en altas latitudes.
- El estiramiento norte-sur crece con latitud más rápido que el estiramiento este-oeste (sec2 φ): La proyección cilíndrica (o cilíndrica central); inadecuada porque la distorsión es aún peor que en la proyección Mercator.
- El estiramiento norte-sur crece con latitud, pero menos rápido que el estiramiento este-oeste: como la proyección cilíndrica Miller (sec 4/5φ).
- Distancias norte-sur no estiradas ni comprimidas (1): proyección equirectangular o "plate carrée".
- La compresión norte-sur es igual a la cosina de la latitud (la reciproca del estiramiento este-oeste): igual-área cilíndrica. Esta proyección tiene muchas especializaciones nombradas que difieren sólo en la constante de escalada, como la ortografía Gall-Peters o Gall (sin distorsionar a los paralelos de 45°), Behrmann (sin distorsionar a los paralelos de 30°), y Lambert cylindrical igual (sin distorsion en el Ecuador). Dado que esta proyección escala las distancias norte-sur por la reciproca del estiramiento este-oeste, preserva el área a expensas de las formas.
En el primer caso (Mercator), la escala este-oeste siempre es igual a la escala norte-sur. En el segundo caso (cilíndrico central), la escala norte-sur excede la escala este-oeste en todas partes fuera del ecuador. Cada caso restante tiene un par de líneas secantes: un par de latitudes idénticas de signo opuesto (o el ecuador) en las que la escala este-oeste coincide con la escala norte-sur.
Las proyecciones cilíndricas normales mapean toda la Tierra como un rectángulo finito, excepto en los dos primeros casos, donde el rectángulo se estira infinitamente alto mientras mantiene el ancho constante.
Cilíndrica transversal
(feminine)Una proyección cilíndrica transversal es una proyección cilíndrica que en el caso de la tangente utiliza un gran círculo a lo largo de un meridiano como línea de contacto para el cilindro.
Ver: Mercator transversal.
Cilíndrica oblicua
(feminine)Una proyección cilíndrica oblicua se alinea con un gran círculo, pero no con el ecuador ni con un meridiano.
Pseudocilíndrico
Las proyecciones pseudocilíndricas representan el meridiano central como un segmento de línea recta. Otros meridianos son más largos que el meridiano central y se inclinan hacia afuera, alejándose del meridiano central. Las proyecciones pseudocilíndricas mapean los paralelos como líneas rectas. A lo largo de los paralelos, cada punto de la superficie se mapea a una distancia del meridiano central que es proporcional a su diferencia de longitud con respecto al meridiano central. Por lo tanto, los meridianos están igualmente espaciados a lo largo de un paralelo dado. En un mapa pseudocilíndrico, cualquier punto más alejado del ecuador que otro punto tiene una latitud más alta que el otro punto, conservando las relaciones norte-sur. Este rasgo es útil para ilustrar fenómenos que dependen de la latitud, como el clima. Los ejemplos de proyecciones pseudocilíndricas incluyen:
- Sinusoidal, que fue la primera proyección pseudocilíndrica desarrollada. En el mapa, como en realidad, la longitud de cada paralelo es proporcional al cosino de la latitud. La zona de cualquier región es verdadera.
- Proyección de Collignon, que en sus formas más comunes representa a cada meridiano como dos segmentos de línea recta, uno de cada polo al Ecuador.
|
|
|
|
|
|
Híbrida
(feminine)La proyección HEALPix combina una proyección cilíndrica de áreas iguales en regiones ecuatoriales con la proyección de Collignon en áreas polares.
Cónico
El término "proyección cónica" se utiliza para referirse a cualquier proyección en la que los meridianos se asignan a líneas igualmente espaciadas que irradian desde el vértice y los círculos de latitud (paralelos) se asignan a arcos circulares centrados en el vértice.
Al hacer un mapa cónico, el creador del mapa elige arbitrariamente dos paralelos estándar. Esos paralelos estándar se pueden visualizar como líneas secantes donde el cono se cruza con el globo o, si el creador del mapa elige el mismo paralelo dos veces, como la línea tangente donde el cono es tangente al globo. El mapa cónico resultante tiene una baja distorsión en escala, forma y área cerca de esos paralelos estándar. Las distancias a lo largo de los paralelos al norte de ambos paralelos estándar o al sur de ambos paralelos estándar se estiran; las distancias a lo largo de los paralelos entre los paralelos estándar se comprimen. Cuando se usa un solo paralelo estándar, las distancias a lo largo de todos los demás paralelos se estiran.
Las proyecciones cónicas que se usan comúnmente son:
- Equidistant conic, que mantiene paralelos uniformemente espaciados a lo largo de los meridianos para preservar una escala de distancia constante a lo largo de cada meridiano, típicamente la misma o similar escala que a lo largo de los paralelos estándar.
- Albers conic, que ajusta la distancia norte-sur entre paralelos no estándar para compensar el estiramiento o compresión este-oeste, dando un mapa de igualdad.
- Lambert conformal conic, que ajusta la distancia norte-sur entre paralelos no estándar para igualar el estiramiento este-oeste, dando un mapa conformado.
Pseudocónico
- Bonne, una proyección de la misma zona en la que la mayoría de los meridianos y paralelos aparecen como líneas curvas. Tiene un estándar configurable paralelo a lo largo del cual no hay distorsión.
- Cordiformo Werner, sobre el cual las distancias son correctas de un polo, así como a lo largo de todos los paralelos.
- American policonic y otras proyecciones en la clase de proyección policonica.
Azimutal (proyecciones sobre un plano)
Las proyecciones azimutales tienen la propiedad de que se conservan las direcciones desde un punto central y, por lo tanto, los grandes círculos que pasan por el punto central se representan mediante líneas rectas en el mapa. Estas proyecciones también tienen simetría radial en las escalas y, por lo tanto, en las distorsiones: las distancias del mapa desde el punto central se calculan mediante una función r(d) de la distancia real d, independiente del ángulo; correspondientemente, los círculos con el punto central como centro se mapean en círculos que tienen como centro el punto central en el mapa.
El mapeo de líneas radiales se puede visualizar imaginando un plano tangente a la Tierra, con el punto central como punto tangente.
La escala radial es r′(d) y la escala transversal r(d)/(R sin d/R) donde R es el radio de la Tierra.
Algunas proyecciones azimutales son verdaderas proyecciones en perspectiva; es decir, se pueden construir mecánicamente, proyectando la superficie de la Tierra extendiendo líneas desde un punto de perspectiva (a lo largo de una línea infinita que pasa por el punto tangente y la antípoda del punto tangente) sobre el plano:
- La proyección gnomónica muestra grandes círculos como líneas rectas. Se puede construir utilizando un punto de perspectiva en el centro de la Tierra. r()d) c#d/R; por lo que incluso un hemisferio ya es infinito en extensión.
- La proyección ortográfica mapea cada punto en la Tierra hasta el punto más cercano en el plano. Se puede construir desde un punto de vista una distancia infinita desde el punto tangente; r()d) cpecadod/R. Puede aparecer hasta un hemisferio en un círculo finito. Fotografías de la Tierra desde lejos, como la Luna, aproximan esta perspectiva.
- Proyección de perspectiva cercana, que simula la vista desde el espacio a una distancia finita y por lo tanto muestra menos que un hemisferio completo, como se utiliza en El mármol azul 2012).
- La proyección Perspectiva General se puede construir utilizando un punto de perspectiva fuera de la Tierra. Las fotografías de la Tierra (como las de la Estación Espacial Internacional) dan esta perspectiva. Es una generalización de la proyección de perspectiva cercana, permitiendo la inclinación.
- La proyección estereográfica, que es conformal, se puede construir utilizando el antipodo del punto tangente como el punto de vista. r()d) c#d/2R; la escala es c/(2)R#2d/2R). Puede mostrar casi toda la superficie de la esfera en un círculo finito. La superficie completa de la esfera requiere un mapa infinito.
Otras proyecciones azimutales no son verdaderas proyecciones en perspectiva:
- Azimuthal equidistant: r()d) cd; es utilizado por operadores de radio aficionados para conocer la dirección para apuntar sus antenas hacia un punto y ver la distancia a él. La distancia desde el punto tangente en el mapa es proporcional a la distancia superficial en la Tierra (para el caso en que el punto tangente es el Polo Norte, vea la bandera de las Naciones Unidas)
- Lambert azimuthal equal-area. Distancia desde el punto tangente en el mapa es proporcional a la distancia recta a través de la Tierra: r()d) cpecadod/2R
- Logaritmic azimuthal se construye para que la distancia de cada punto desde el centro del mapa sea el logaritmo de su distancia desde el punto tangente en la Tierra. r()d) cInd/d0); lugares más cercanos que a una distancia igual a la constante d0 no se muestran.
Poliédrica
(feminine)Las proyecciones de mapas poliédricos usan un poliedro para subdividir el globo terráqueo en caras y luego proyectan cada cara al globo terráqueo. La proyección de mapa poliédrico más conocida es el mapa Dymaxion de Buckminster Fuller.
Proyecciones por preservación de una propiedad métrica
Conforme
Las proyecciones cartográficas conformes u ortomórficas preservan los ángulos localmente, lo que implica que asignan círculos infinitesimales de tamaño constante en cualquier parte de la Tierra a círculos infinitesimales de diferentes tamaños en el mapa. Por el contrario, las asignaciones que no son conformes distorsionan la mayoría de estos pequeños círculos en elipses de distorsión. Una consecuencia importante de la conformidad es que los ángulos relativos en cada punto del mapa son correctos, y la escala local (aunque varía a lo largo del mapa) en todas las direcciones alrededor de cualquier punto es constante. Estas son algunas proyecciones conformes:
- Mercator: Rhumb lines are represented by straight segments
- Mercator transversal
- Stereographic: Cualquier círculo de una esfera, grande y pequeña, mapas a un círculo o línea recta.
- Roussilhe
- Lambert conformal conic
- Peirce quincuncial projection
- proyección hemisférica de Adams en un cuarto
- Proyección hemisférica en un cuarto
Áreas iguales
Los mapas de áreas iguales conservan la medida del área y, por lo general, distorsionan las formas para lograrlo. Los mapas de áreas iguales también se denominan equivalentes o autálicos. Estas son algunas proyecciones que preservan el área:
- Albers conic
- Bonne
- Bottomley
- Collignon
- Zona de igualdad cilíndrica
- Eckert II, IV y VI
- Igualdad de Tierra
- Ortográfico Gall (también conocido como Gall-Peters, o Peters, proyección)
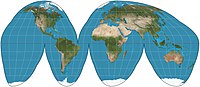
- La homolosina de Goode
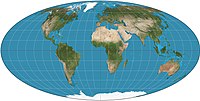
- Hammer
- Hobo-Dyer
- Lambert azimuthal equal-area
- Lambert cylindrical equal-area
- Mollweide
- Sinusoidal
- Strebe 1995
- La proyección poliedral de la misma zona de Snyder, utilizada para redes geodésicas.
- Tobler hyperelliptical
- Werner
Equidistante
Si la longitud del segmento de línea que conecta dos puntos proyectados en el plano es proporcional a la distancia geodésica (superficie más corta) entre los dos puntos no proyectados en el globo, entonces decimos que la distancia se ha conservado entre esos dos puntos. Una proyección equidistante conserva las distancias de uno o dos puntos especiales a todos los demás puntos. El punto o puntos especiales pueden estirarse en un segmento de línea o curva cuando se proyectan. En ese caso, el punto en el segmento de línea o curva más cercano al punto que se está midiendo debe usarse para medir la distancia.
- Placa de carreo: Las distancias de los dos polos se conservan, en aspecto ecuatorial.
- Azimuthal equidistant: Se conservan distancias del centro y del borde.
- Equidistant conic: Las distancias de los dos polos se conservan, en aspecto ecuatorial.
- Werner cordiform Las distancias del Polo Norte se conservan, en aspecto ecuatorial.
- Equidista de dos puntos: Dos "puntos de control" son elegidos arbitrariamente por el fabricante de mapas; se conservan distancias de cada punto de control.
Gnomónico
Los grandes círculos se muestran como líneas rectas:
- Proyección Gnomónica
Retroazimutal
La dirección a una ubicación fija B (el rumbo en la ubicación inicial A de la ruta más corta) corresponde a la dirección en el mapa de A a B:
- Littrow - la única proyección retroazimutal conformacional
- Hammer retroazimuthal - también preserva la distancia desde el punto central
- Craig retroazimuthal aka Meca o Qibla también tiene meridianos verticales
Proyecciones de compromiso
Las proyecciones de compromiso abandonan la idea de preservar perfectamente las propiedades métricas y buscan, en cambio, lograr un equilibrio entre las distorsiones o simplemente hacer que las cosas se vean bien. La mayoría de estos tipos de proyecciones distorsionan la forma en las regiones polares más que en el ecuador. Estas son algunas proyecciones de compromiso:
- Robinson
- van der Grinten
- Miller cilíndrico
- Winkel Tripel
- Buckminster Fuller Dymaxion
- Mapa de mariposa de B. J. S. Cahill
- Kavrayskiy VII proyección
- Proyección Wagner VI
- Chamberlin trimetric
- El cordiformo de Oronce Finé
- Proyección de AuthaGraph
¿Qué proyección es mejor?
Las matemáticas de la proyección no permiten que ninguna proyección de mapa en particular sea la mejor para todo. Siempre habrá algo distorsionado. Por lo tanto, existen muchas proyecciones para servir a los muchos usos de los mapas y su amplia gama de escalas.
Los sistemas cartográficos nacionales modernos suelen emplear un Mercator transversal o una variante cercana para mapas a gran escala con el fin de preservar la conformidad y la baja variación de escala en áreas pequeñas. Para mapas de escala más pequeña, como los que abarcan continentes o el mundo entero, muchas proyecciones son de uso común según su idoneidad para el propósito, como Winkel tripel, Robinson y Mollweide. Los mapas de referencia del mundo a menudo aparecen en las proyecciones de compromiso. Debido a las distorsiones inherentes a cualquier mapa del mundo, la elección de la proyección se convierte en gran medida en estética.
Los mapas temáticos normalmente requieren una proyección de área equivalente para que los fenómenos por unidad de área se muestren en la proporción correcta. Sin embargo, representar proporciones de áreas correctamente necesariamente distorsiona las formas más que muchos mapas que no son de áreas iguales.
La proyección de Mercator, desarrollada con fines de navegación, se ha utilizado a menudo en mapas del mundo donde otras proyecciones habrían sido más apropiadas. Este problema ha sido reconocido durante mucho tiempo incluso fuera de los círculos profesionales. Por ejemplo, un editorial de 1943 del New York Times afirma:
Ha llegado el momento de descartar [el Mercator] por algo que representa a los continentes y direcciones menos engañosamente... Aunque su uso... ha disminuido... sigue siendo muy popular como un mapa de pared aparentemente en parte porque, como un mapa rectangular, llena un espacio de pared rectangular con más mapa, y claramente porque su familiaridad genera más popularidad.
Una controversia en la década de 1980 sobre el mapa de Peters motivó a la Asociación Cartográfica Estadounidense (ahora la Sociedad de Información Geográfica y Cartografía) a producir una serie de folletos (incluido Qué mapa es el mejor) diseñados para educar a los público sobre las proyecciones de mapas y la distorsión en los mapas. En 1989 y 1990, después de un debate interno, siete organizaciones geográficas de América del Norte adoptaron una resolución recomendando no utilizar ninguna proyección rectangular (incluidas Mercator y Gall-Peters) para mapas de referencia del mundo.
Contenido relacionado
West Lafayette, Indiana
Geografía de Bélgica
Agua salobre