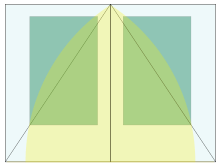
Proporción áurea
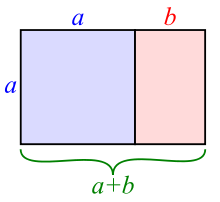
En matemáticas, dos cantidades están en ratio de oro si su relación es la misma que la proporción de su suma a la mayor de las dos cantidades. Expresado algebraicamente, para cantidades a{displaystyle a} y b{displaystyle b} con b>0}" xmlns="http://www.w3.org/1998/Math/MathML">a■b■0{displaystyle a fielb} b > 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/dc57e5721ebc7b851b968ea2545913848bf7a01e" style="vertical-align: -0.338ex; width:9.587ex; height:2.176ex;"/>,
donde la letra griega phi (φ φ {displaystyle varphi } o φ φ {displaystyle phi }) denota la relación de oro. La constante φ φ {displaystyle varphi } satisfice la ecuación cuadrática φ φ 2=φ φ +1{displaystyle varphi ^{2}=varphi +1} y es un número irracional con un valor
La proporción áurea fue llamada proporción extrema y media por Euclides, y proporción divina por Luca Pacioli, y también recibe varios otros nombres.
Los matemáticos han estudiado las propiedades de la relación de oro desde la antigüedad. Es la relación de la diagonal de un pentágono regular a su lado y así aparece en la construcción del dodecaedro y icosahedro. Un rectángulo dorado, es decir, un rectángulo con una relación de aspecto φ φ {displaystyle varphi }—se puede cortar en un cuadrado y un rectángulo más pequeño con la misma relación de aspecto. La relación de oro se ha utilizado para analizar las proporciones de objetos naturales y sistemas artificiales como los mercados financieros, en algunos casos basados en ajustes dudosos a los datos. La relación de oro aparece en algunos patrones de naturaleza, incluyendo el arreglo espiral de hojas y otras partes de vegetación.
Algunos artistas y arquitectos del siglo XX, incluidos Le Corbusier y Salvador Dalí, han proporcionado sus obras para aproximarse a la proporción áurea, creyendo que es estéticamente agradable. Estos usos suelen aparecer en forma de rectángulo dorado.
Cálculo
Dos cantidades a{displaystyle a} y b{displaystyle b} están en ratio de oro φ φ {displaystyle varphi } si
Un método para encontrar φ φ {displaystyle varphi }La forma cerrada comienza con la fracción izquierda. Simplificar la fracción y sustituir la reciprocidad b/a=1/φ φ {displaystyle b/a=1/varphi },
Por lo tanto,
Multiplying by φ φ {displaystyle varphi } da
que se puede reorganizar para
La fórmula cuadrática produce dos soluciones:
Porque... φ φ {displaystyle varphi } es una relación entre las cantidades positivas, φ φ {displaystyle varphi } es necesariamente la raíz positiva. La raíz negativa es de hecho el inverso negativo − − 1φ φ {displaystyle - ¿Qué? }, que comparte muchas propiedades con la relación de oro.
Historia
Según Mario Livio,
Algunas de las mentes matemáticas más grandes de todas las edades, desde Pitágoras y Euclides en la antigua Grecia, a través del matemático medieval italiano Leonardo de Pisa y el astrónomo renacentista Johannes Kepler, hasta figuras científicas actuales como el físico de Oxford Roger Penrose, han pasado horas interminables sobre esta relación simple y sus propiedades.... Biólogos, artistas, músicos, historiadores, arquitectos, psicólogos e incluso místicos han meditado y debatido la base de su ubicuidad y atractivo. De hecho, es probablemente justo decir que la relación de oro ha inspirado a los pensadores de todas las disciplinas como ningún otro número en la historia de las matemáticas.
—La relación de oro: La historia de Phi, el número más asombroso del mundo
Los matemáticos de la antigua Grecia primero estudiaron la proporción áurea debido a su frecuente aparición en la geometría; la división de una recta en "proporción media y extrema" (la sección áurea) es importante en la geometría de los pentagramas y pentágonos regulares. Según una historia, Hippasus, matemático del siglo V a. C., descubrió que la proporción áurea no era ni un número entero ni una fracción (un número irracional), lo que sorprendió a los pitagóricos. Los Elementos de Euclides (c. 300 aC) proporciona varias proposiciones y sus pruebas empleando la proporción áurea, y contiene su primera definición conocida que procede como sigue:
Se dice que una línea recta ha sido cortada en relación extrema y media cuando, como toda la línea es al segmento mayor, así es mayor al menor.
La proporción áurea se estudió periféricamente durante el próximo milenio. Abu Kamil (c. 850–930) lo empleó en sus cálculos geométricos de pentágonos y decágonos; sus escritos influyeron en los de Fibonacci (Leonardo de Pisa) (c. 1170-1250), quien usó la proporción en problemas de geometría relacionados pero no observó que estuviera conectado con los números de Fibonacci.
Luca Pacioli nombró a su libro Divinaproporcione (1509) en honor a la proporción; el libro, en gran parte plagiado de Piero della Francesca, exploró sus propiedades, incluida su aparición en algunos de los sólidos platónicos. Leonardo da Vinci, quien ilustró el libro de Pacioli, llamó a la proporción la sectio aurea ('sección dorada'). Aunque a menudo se dice que Pacioli abogó por la aplicación de la proporción áurea para producir proporciones agradables y armoniosas, Livio señala que la interpretación se remonta a un error en 1799, y que Pacioli en realidad abogó por el sistema Vitruvio de proporciones racionales. Pacioli también vio un significado religioso católico en la proporción, lo que llevó al título de su obra. Matemáticos del siglo XVI como Rafael Bombelli resolvieron problemas geométricos usando la razón.
El matemático alemán Simon Jacob (d. 1564) señaló que los números consecutivos de Fibonacci convergen a la relación de oro; esto fue redescubierto por Johannes Kepler en 1608. La primera aproximación decimal conocida de la relación dorada (inversa) se declaró como "sobre 0.6180340{displaystyle 0.6180340}" en 1597 por Michael Maestlin de la Universidad de Tübingen en una carta a Kepler, su antiguo estudiante. El mismo año, Kepler escribió a Maestlin del triángulo Kepler, que combina la relación de oro con el teorema pitagórico. Kepler dijo:
La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras, el otro la división de una línea en relación extrema y media. El primero que podemos comparar con una masa de oro, el segundo que podemos llamar una joya preciosa.
Los matemáticos del siglo XVIII Abraham de Moivre, Nicolaus I Bernoulli y Leonhard Euler utilizaron una fórmula basada en la proporción áurea que encuentra el valor de un número de Fibonacci en función de su ubicación en la secuencia; en 1843, esto fue redescubierto por Jacques Philippe Marie Binet, por quien se denominó "fórmula de Binet". Martin Ohm utilizó por primera vez el término alemán goldener Schnitt ('sección dorada') para describir la relación en 1835. James Sully utilizó el término equivalente en inglés en 1875.
Para 1910, el inventor Mark Barr comenzó a usar la letra griega Phi ()φ φ {displaystyle {boldsymbol {varphi} }) como símbolo de la relación de oro. También ha estado representado por tau ()τ τ {displaystyle {boldsymbol {tau} }), la primera letra del griego antiguo τομё ('cut' o 'sección').
El sistema de construcción zome, desarrollado por Steve Baer a fines de la década de 1960, se basa en el sistema de simetría del icosaedro/dodecaedro y utiliza la proporción áurea de forma ubicua. Entre 1973 y 1974, Roger Penrose desarrolló el mosaico de Penrose, un patrón relacionado con la proporción áurea tanto en la proporción de áreas de sus dos mosaicos rómbicos como en su frecuencia relativa dentro del patrón. Esto ganó interés después del descubrimiento ganador del Nobel de Dan Shechtman en 1982 de los cuasicristales con simetría icosaédrica, que poco después se explicaron a través de analogías con el mosaico de Penrose.
Matemáticas
Irracionalidad
La proporción áurea es un número irracional. A continuación hay dos breves pruebas de irracionalidad:
Contradicción de una expresión en términos mínimos

Recuerda que:
el todo es a la parte más larga ya que la parte más larga es a la parte más corta.
Si llamamos al todo n{displaystyle n} y la parte más larga m,{displaystyle m,} entonces la segunda declaración arriba se convierte
Decir que la relación de oro φ φ {displaystyle varphi } es un medio racional φ φ {displaystyle varphi } es una fracción n/m{displaystyle No. Donde n{displaystyle n} y m{displaystyle m} son enteros. Podemos tomar n/m{displaystyle No. ser en términos más bajos y n{displaystyle n} y m{displaystyle m} para ser positivo. Pero si n/m{displaystyle No. es en términos más bajos, entonces el valor igual m/()n− − m){displaystyle m/(n-m)} está en términos aún más bajos. Esa es una contradicción que se deriva del supuesto de que φ φ {displaystyle varphi } es racional.
Por irracionalidad de √5
Otra prueba corta – quizás más comúnmente conocida – de la irracionalidad de la relación dorada hace uso del cierre de números racionales bajo adición y multiplicación. Si φ φ =12()1+5){displaystyle varphi ={2} {1+{sqrt {}}} es racional, entonces 2φ φ − − 1=5{displaystyle 2varphi -1={sqrt {}} es también racional, que es una contradicción si ya se sabe que la raíz cuadrada de todos los números naturales no cuadrado es irracional.
Polinomio mínimo
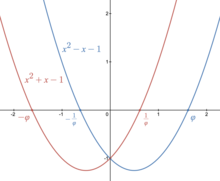
La proporción áurea también es un número algebraico e incluso un número entero algebraico. tiene polinomio minimo
Este polinomio cuadrático tiene dos raíces, φ φ {displaystyle varphi } y − − φ φ − − 1.{displaystyle - Navarra.
La proporción áurea también está estrechamente relacionada con el polinomio
que tiene raíces − − φ φ {displaystyle -varphi } y φ φ − − 1.{displaystyle varphi ^{-1} Como raíz de un polinomio cuadrático, la relación de oro es un número constructible.
Proporción áurea conjugada y potencias
La raíz conjugada al mínimo polinomio x2− − x− − 1{displaystyle x^{2}-x-1} es
El valor absoluto de esta cantidad ()0.618...... {displaystyle 0.618ldots}) corresponde a la relación de longitud tomada en orden inverso (longitud de segmento corta sobre longitud de segmento más larga, b/a{displaystyle b/a}).
Esto ilustra la propiedad única de la proporción áurea entre los números positivos, que
o su inversa:
El conjugado y la definición de la relación cuadrática polinomio conducen a valores decimales que tienen su parte fraccional en común con φ φ {displaystyle varphi }:
La secuencia de poderes φ φ {displaystyle varphi } contiene estos valores 0.618033...... ,{displaystyle 0.618033ldots} 1.0,{displaystyle 1.0,} 1.618033...... ,{displaystyle 1.618033ldots} 2.618033...... ;{displaystyle 2.618033ldots;} más generalmente, cualquier poder de φ φ {displaystyle varphi } es igual a la suma de los dos poderes inmediatamente anteriores:
Como resultado, se puede descomponer fácilmente cualquier poder φ φ {displaystyle varphi } en un múltiplo de φ φ {displaystyle varphi } y una constante. Los números múltiples y constantes son siempre los números adyacentes de Fibonacci. Esto conduce a otra propiedad de los poderes positivos φ φ {displaystyle varphi }:
Si ⌊ ⌊ n/2− − 1⌋ ⌋ =m,{displaystyle lfloor n/2-1rfloor =m,} entonces:
Fracción continua y raíz cuadrada
La fórmula φ φ =1+1/φ φ {displaystyle varphi =1+1/varphi } puede ampliarse recursivamente para obtener una fracción continua para la relación de oro:
De hecho, es la forma más simple de una fracción continua, junto con su forma recíproca:
Los convergentes de estas fracciones continuas ()1/1,{displaystyle 1/1,} 2/1,{displaystyle 2/1,} 2/1,{displaystyle 2/1,} 3/2,{displaystyle 3/2,} 5/3,{displaystyle 5/3,} 8/5,{displaystyle 8/5,} 13/8,{displaystyle 13/8,}... o 1/1,{displaystyle 1/1,} 1/2,{displaystyle 1/2,} 2/3,{displaystyle 2/3,} 3/5,{displaystyle 3/5,} 5/8,{displaystyle 5/8,} 8/13,{displaystyle 8/13,}...) son ratios de números de Fibonacci sucesivos. Los términos consistentemente pequeños en su fracción continua explican por qué los aproximadores convergen tan lentamente. Esto hace que la relación de oro sea un caso extremo de la desigualdad Hurwitz para aproximaciones de la diofantina, que afirma que por cada irracional .. {displaystyle xi }, hay infinitamente muchas fracciones distintas p/q{displaystyle p/q} tal que,
<math alttext="{displaystyle left|xi -{frac {p}{q}}right|Silencio.. − − pqSilencio.15q2.{displaystyle left durablexi - {frac {fnMicrosoft}fnMicroc {1}{sqrt {5}q^{2}}}}<img alt="{displaystyle left|xi -{frac {p}{q}}right|
Esto significa que la constante 5{displaystyle {sqrt {5}} no se puede mejorar sin excluir la relación de oro. Es, de hecho, el menor número que debe ser excluido para generar aproximaciones más cercanas de tales números Lagrange.
A continued square root form for φ φ {displaystyle varphi } puede obtenerse φ φ 2=1+φ φ {displaystyle varphi ^{2}=1+varphi }, cediendo:
Relación con los números de Fibonacci y Lucas
Los números de Fibonacci y Lucas tienen una relación intrincada con la relación de oro. En la secuencia Fibonacci, cada número es igual a la suma de los dos anteriores, comenzando con la secuencia base 0,1{displaystyle 0,1}:
La secuencia de los números de Lucas (para no confundirse con las secuencias generalizadas de Lucas, de las cuales esto es parte) es como la secuencia de Fibonacci, en la que cada término es la suma de las dos anteriores, sin embargo en cambio comienza con 2,1{displaystyle 2,1}:
Excepcionalmente, la proporción áurea es igual al límite de las proporciones de términos sucesivos en la secuencia de Fibonacci y la secuencia de números de Lucas:
En otras palabras, si un número de Fibonacci y Lucas está dividido por su predecesor inmediato en la secuencia, el cociente se aproxima φ φ {displaystyle varphi }.
Por ejemplo, F16F15=987610=1.6180327...... ,{displaystyle {frac {f}{F_{15}}={frac {987}{610}=1.6180327ldots} y L16L15=22071364=1.6180351...... .{fnMicroc} {L_{16}{L_{15}}={frac} {f} {f} {f}} {f}} {f}}}}} {f}}}} {f}}} {f} {f}}}}} {f}} {f}}}}}} {f}}}}}} {f}}}}}}}} {f}}} {f}} {f}}}}}}}}}}}}}}} {f} {f} {f} {f} {f} {f}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}f}}}} {f} {f} {f} {f} {f} {f} {f} {f}f}f}f}f}f}}}}f {2207}{1364}=1.6180351ldots.}
Estas aproximaciones son alternadamente inferiores y superiores a las φ φ ,{displaystyle varphi} y converger φ φ {displaystyle varphi } mientras los números de Fibonacci y Lucas aumentan.
Las expresiones de forma cerrada para las secuencias de Fibonacci y Lucas que involucran la proporción áurea son:
Combinando ambas fórmulas arriba, se obtiene una fórmula para φ φ n{displaystyle varphi ^{n} que implica tanto los números de Fibonacci como Lucas:
Entre Fibonacci y Lucas número uno puede deducir L2n=5Fn2+2()− − 1)n=Ln2− − 2()− − 1)n,{displaystyle L_{2n}=5F_{n}{2}+2(-1)^{n}=L_{n}^{2}-2(-1)^{n} } que simplifica para expresar el límite del cociente de los números de Lucas por los números de Fibonacci igual a la raíz cuadrada de cinco:
De hecho, declaraciones mucho más fuertes son verdaderas:
- SilencioLn− − 5FnSilencio=2φ φ n→ → 0{displaystyle vert L_{n}-{sqrt {5}F_{n}vert ={frac {2}{varphi ^{n}}to} 0},
- ()L3n/2)2=5()F3n/2)2+()− − 1)n{displaystyle (L_{3n}/2)^{2}=5(F_{3n}/2)^{2}+(-1)^{n}.
Estos valores describen φ φ {displaystyle varphi } como una unidad fundamental del campo número algebraico Q()5){displaystyle mathbb {Q} ({sqrt {5})}.
Los poderes sucesivos de la relación de oro obedecen a la recurrencia Fibonacci, es decir. φ φ n+1=φ φ n+φ φ n− − 1.{displaystyle varphi ^{n+1}=varphi ^{n}+varphi ^{n-1}
La reducción a una expresión lineal se puede lograr en un solo paso usando:
Esta identidad permite cualquier polinomio en φ φ {displaystyle varphi } a ser reducido a una expresión lineal, como en:
Los números de Fibonacci consecutivos también se pueden usar para obtener una fórmula similar para la proporción áurea, aquí por suma infinita:
En particular, los poderes de φ φ {displaystyle varphi } a los números de Lucas (en orden, excepto los dos primeros poderes, φ φ 0{displaystyle varphi ^{0} y φ φ {displaystyle varphi }, están en orden inverso):
y así sucesivamente. Los números Lucas también generan directamente poderes de la relación de oro; para n≥ ≥ 2{displaystyle ngeq 2}:
Rooted en su relación interconectante con la relación de oro es la noción de que la suma de tercero Los números consecutivos de Fibonacci equivalen a un número de Lucas, es decir, Ln=Fn− − 1+Fn+1{displaystyle L_{n}=F_{n-1}+F_{n+1}; y, en particular, eso Ln=F2nFn{displaystyle {L_{n}={frac} {fn} {fn}} {fn}} {fn}}} {fn}}}} {fn}}}} {fn}}}}} {f}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.
Tanto la secuencia de Fibonacci como la secuencia de números de Lucas se pueden usar para generar formas aproximadas de la espiral áurea (que es una forma especial de una espiral logarítmica) usando cuartos de círculo con radios de estas secuencias, que difieren solo ligeramente de la verdadera espiral logarítmica dorada. Espiral de Fibonacci es generalmente el término utilizado para las espirales que se aproximan a las espirales doradas utilizando cuadrados y cuartos de círculo secuenciados por números de Fibonacci.
Geometría
La proporción áurea ocupa un lugar destacado en la geometría. Por ejemplo, está intrínsecamente involucrado en la simetría interna del pentágono, y se extiende para formar parte de las coordenadas de los vértices de un dodecaedro regular, así como las de un 5 celdas. También aparece en el triángulo de Kepler y en los mosaicos de Penrose, así como en varios otros politopos.
Construcción
División por división interior
- Tener un segmento de línea AB,{displaystyle AB,} construir un perpendicular BC{displaystyle BC! punto B,{displaystyle B,} con BC{displaystyle BC! la mitad de la longitud AB.{displaystyle AB.} Dibuja la hipotenusa AC.{displaystyle AC.
- Dibujar un arco con centro C{displaystyle C} y radio BC.{displaystyle BC.} Este arco interseca la hipotenusa AC{displaystyle AC. punto D.{displaystyle D.}
- Dibujar un arco con centro A{displaystyle A} y radio AD.{displaystyle AD.} Este arco interseca el segmento de línea original AB{displaystyle AB} punto S.{displaystyle S.} Punto S{displaystyle S. divide el segmento de línea original AB{displaystyle AB} en segmentos de línea AS{displaystyle ¿Cómo? y SB{displaystyle SB. con longitudes en la relación de oro.
División por división exterior
- Dibujar un segmento de línea AS{displaystyle ¿Cómo? y construir fuera del punto S{displaystyle S. a segmento SC{displaystyle SC! perpendicular a AS{displaystyle ¿Cómo? y con la misma longitud AS.{displaystyle - Sí.
- Hacer bisectar el segmento de línea AS{displaystyle ¿Cómo? con M.{displaystyle M.}
- Un arco circular alrededor M{displaystyle M} con radio MC{displaystyle MC! intersectos en punto B{displaystyle B} línea recta a través de puntos A{displaystyle A} y S{displaystyle S. (también conocido como la extensión de AS{displaystyle ¿Cómo?). La relación entre AS{displaystyle ¿Cómo? al segmento construido SB{displaystyle SB. es la relación de oro.
Ejemplos de aplicación que puede ver en los artículos Pentágono con una longitud de lado determinada, Decágono con un círculo circunscrito determinado y Decágono con una longitud de lado determinada.
Los dos algoritmos anteriores que se muestran arriba producen construcciones geométricas que determinan dos segmentos de línea alineados donde la proporción entre el más largo y el más corto es la proporción áurea.
Ángulo de oro
Cuando dos ángulos que hacen un círculo completo tienen medidas en la relación de oro, el menor se llama el ángulo dorado, con medida g:: {textstyle gcolon }
Este ángulo se produce en los patrones de crecimiento de las plantas como el espacio óptimo de los brotes de las hojas alrededor de los tallos de las plantas para que las hojas sucesivas no bloqueen la luz solar de las hojas que se encuentran debajo de ellas.
Espiral dorada
Las espirales logarítmicas son espirales autosimilares donde las distancias cubiertas por giro están en progresión geométrica. Importantemente, los triángulos dorados isosceles pueden ser encasillados por una espiral logarítmica dorada, tal que giros sucesivos de una espiral generan nuevos triángulos dorados dentro. Este caso especial de espirales logarítmicas se llama el espiral dorada, y exhibe crecimiento continuo en relación dorada. Eso es, para todos 90∘ ∘ {displaystyle 90^{circ }} giro, hay un factor de crecimiento φ φ {displaystyle varphi }. Como se ha mencionado anteriormente, estos espirales doradas puede ser aproximado por los círculos trimestrales generados por Fibonacci y Lucas cuadrados de tamaño número que se juntan. En su forma exacta, pueden describirse por la ecuación polar con ()r,Silencio Silencio ){displaystyle (r,theta)}:
Como con cualquier espiral logarítmica, para r=aebSilencio Silencio {displaystyle r=ae^{btheta } con ebSilencio Silencio right=φ φ {displaystyle e^{btheta _{mathrm {right} }=varphi } en ángulos rectos:
Su pendiente polar α α {displaystyle alpha } se puede calcular utilizando # α α =b{displaystyle tan alpha =b} junto SilenciobSilencio{displaystyle Silencioso de arriba,
Tiene un ángulo complementario, β β {displaystyle beta }:
Las espirales doradas se pueden colocar simétricamente dentro de pentágonos y pentagramas también, de modo que las copias fractales de la geometría subyacente se reproduzcan en todas las escalas.
En triángulos, cuadriláteros y pentágonos
Construcción de Odom
George Odom encontró una construcción para φ φ {displaystyle varphi } implicando un triángulo equilátero: si un triángulo equilátero está inscrito en un círculo y el segmento de línea que une los puntos intermedios de dos lados se produce para intersectar el círculo en cualquiera de dos puntos, entonces estos tres puntos están en proporción dorada.
Triángulo de Kepler
El triángulo de Kepler, llamado así por Johannes Kepler, es el único triángulo rectángulo con lados en progresión geométrica:
El triángulo Kepler también se puede entender como el triángulo derecho formado por tres cuadrados cuyas áreas también están en progresión geométrica dorada 1:φ φ :φ φ 2{displaystyle 1mathbin {:} varphi mathbin {:} varphi ^{2}.
Fittingly, el Pythagorean significa para φ φ ± ± 1{displaystyle varphi pm 1} son precisamente 1{displaystyle 1}, φ φ {displaystyle varphi }, y φ φ 2{displaystyle varphi ^{2}. Es a partir de estas ratios que podemos expresar geométricamente el polinomio cuadrático fundamental para definir φ φ {displaystyle varphi } con el teorema pitagórico; es decir, φ φ 2=φ φ +1{displaystyle varphi ^{2}=varphi +1}.
El interior del radio de un triángulo isósceles es mayor cuando el triángulo está compuesto por dos triángulos de Kepler especulares, de modo que sus bases se encuentran en la misma línea. Además, el triángulo isósceles de perímetro dado con el semicírculo más grande posible es uno de dos triángulos de Kepler reflejados.
Para un triángulo Kepler con longitud lateral más pequeña s{displaystyle s}, el área y los ángulos internos agudos son:
Triángulo dorado
A triángulo dorado se caracteriza como un isosceles ABC{displaystyle triangle ABC} con la propiedad que bisecte el ángulo ∠ ∠ C{displaystyle angle C} produce nuevos triángulos isosceles agudos y obtusos CXB{displaystyle triangle CXB} y CXA{displaystyle triangle CXA} que son similares al original, así como en la longitud de la pierna a la base de 1:φ φ {displaystyle 1:varphi } y φ φ :φ φ 2{displaystyle varphi:varphi ^{2}, respectivamente.
El triángulo isosceles agudo se llama a veces triángulo sublime, y la relación de su base con sus lados de longitud igual φ φ {displaystyle varphi }. Su ángulo de ápice ∠ ∠ BCX{displaystyle angle BCX} es igual a:
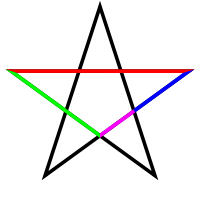
Ambos ángulos base del triángulo dorado isosceles igual 72∘ ∘ {displaystyle 72^{circ }} grados cada uno, ya que la suma de los ángulos de un triángulo debe igual 180∘ ∘ {displaystyle 180^{circ } grados. Es el único triángulo tener sus tres ángulos en 1:2:2{displaystyle 1:2:2} ratio. Un pentagrama regular contiene cinco triángulos sublimes agudos, y un decágono regular contiene diez, ya que cada dos vértices conectados al centro forman triángulos dorados agudos.
El triángulo isosceles obtuso se llama a veces gnomo dorado, y la relación de su base con sus otros lados es la recíproca de la relación de oro, 1/φ φ {displaystyle 1/varphi }. La medida de su ángulo del ápice ∠ ∠ AXC{displaystyle angle AXC} es:
Sus dos ángulos base son iguales 36∘ ∘ {displaystyle 36^{circ } cada uno. Es el único triángulo cuyos ángulos internos están en 1:1:3{displaystyle 1:1:3} ratio. Sus ángulos de base, siendo igual a 36∘ ∘ {displaystyle 36^{circ }, son la misma medida que la del ángulo del ápice del triángulo dorado agudo. Cinco gnomos dorados se pueden crear desde los lados adyacentes de un pentágono cuyos vértices no coincidentes se unen a una diagonal del pentágono.
Apropiadamente, la relación del área del gnomo dorado obtuso con la del triángulo sublime agudo está en 1:φ φ {displaystyle 1:varphi } ratio dorada. Bisecando un ángulo base dentro de un triángulo sublime produce un gnomo dorado, y otro un triángulo sublime. Bisecando el ángulo del ápice de un gnomo dorado en 1:2{displaystyle 1:2} ratio produce dos nuevos triángulos dorados, también. triángulos dorados que están descompuestos más adelante como este en pares de isosceles y triángulos dorados obtusos son conocidos como triángulos Robinson.
Rectángulo dorado

| Dibuja un cuadrado. |
| Dibuja una línea desde el punto medio de un lado de la plaza a una esquina opuesta. |
| Use esa línea como el radio para dibujar un arco que define la altura del rectángulo. |
| Completa el rectángulo dorado. |
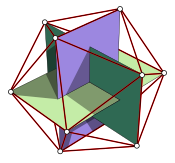
La relación de oro proporciona las longitudes laterales adyacentes de una rectángulo dorado dentro 1:φ φ {displaystyle 1:varphi } ratio. Los rectángulos dorados apilados producen rectángulos dorados de nuevo, y la eliminación o adición de cuadrados de hojas rectángulos dorados todavía proporcionadas en φ φ {displaystyle varphi } ratio. Pueden ser generados por espirales doradas, a través de sucesivos cuadrados y círculos trimestrales de tamaño número Fibonacci y Lucas. Destacan en el icosahedron, así como en el dodecahedron (ver sección abajo para más detalles).
Rombo dorado
A rombo dorado es un rombo cuyas diagonales son proporcionales a la relación de oro, más comúnmente 1:φ φ {displaystyle 1:varphi }. Para un rombo de tales proporciones, su ángulo agudo y ángulos obtusos son:
Las longitudes de sus diagonales cortos y largos d{displaystyle d} y D{displaystyle D}, en términos de longitud lateral a{displaystyle a} son:
Su área, en términos de a{displaystyle a}, y d{displaystyle d}:
Su inradius, en términos de lado a{displaystyle a}:
Característica del rombo dorado en el triacontaedro rómbico (ver la sección a continuación). También se encuentran en el romboedro áureo, el dodecaedro de Bilinski y el hexacontaedro rómbico.
Pentágono y pentagrama
En un pentágono regular la relación de una diagonal a un lado es la relación de oro, mientras que se intersectan diagonales entre sí en la relación de oro. Las propiedades de relación de oro de un pentágono regular se pueden confirmar aplicando el teorema de Ptolomeo al cuadrilátero formado por la eliminación de uno de sus vértices. Si el borde largo del cuadrilátero y las diagonales son b,{displaystyle b,} y los bordes cortos son a,{displaystyle a,} entonces el teorema de Ptolemy da b2=a2+ab{displaystyle b^{2}=a^{2}+ab} que rinde,
Los segmentos diagonales de un pentágono forman un pentagrama, o un polígono estrella de cinco puntos, cuya geometría se describe por quintasencialmente por φ φ {displaystyle varphi }. Principalmente, cada intersección de bordes secciones otros bordes en la relación dorada. La relación de la longitud del segmento más corto al segmento ligado por los dos bordes intersecantes (es decir, un lado del pentágono invertido en el centro del pentagrama) es φ φ ,{displaystyle varphi} como muestra la ilustración de cuatro colores.
Un pentagrama tiene diez triángulos isosceles: cinco son agudos triángulos sublimes, y cinco son obtuso gnomos dorados. En todos ellos, la relación del lado más largo con el lado más corto es φ φ .{displaystyle varphi.} Estos pueden ser descompuestos más adelante en pares de triángulos de oro Robinson, que se hacen relevantes en los revestimientos Penrose.
De lo contrario, la geometría pentagonal y pentagramatica nos permite calcular los siguientes valores para φ φ {displaystyle varphi }:
Teselaciones de Penrose
La proporción áurea aparece de forma destacada en el teselado de Penrose, una familia de teselados aperiódicos del plano desarrollados por Roger Penrose, inspirados en la observación de Johannes Kepler de que los pentagramas, los decágonos y otras formas podría llenar los huecos que las formas pentagonales solas dejan cuando se juntan. Se han estudiado varias variaciones de este mosaico, todos cuyos prototipos exhiben la proporción áurea:
- La versión original de Penrose de este revestimiento utiliza cuatro formas: pentágonos regulares y pentagramas, figuras "lancha" con tres puntos de un pentagrama, y rhombi "diamond".
- El kite y dart Penrose tiling utiliza kits con tres ángulos interiores de 72° y un ángulo interior de 144°, y dardos, concave quadrilaterals con dos ángulos interiores de 36°, uno de 72°, y un ángulo no-convexo de 216°. Las reglas especiales de juego restringen cómo los azulejos se pueden encontrar en cualquier borde, dando lugar a siete combinaciones de azulejos en cualquier vértice. Tanto los kites como los dardos tienen lados de dos longitudes, en la relación de oro entre sí. Las áreas de estas dos formas de azulejos también están en la relación de oro entre sí.
- El azulejo de penrose rhombic contiene dos tipos de rombo, un rimbo delgado con ángulos de 36° y 144°, y un grueso rombo con ángulos de 72° y 108°. De nuevo, estos rhombi se pueden descomponer en triángulos Robinson dorados. Todas las longitudes laterales son iguales, pero la relación de la longitud de los lados con la diagonal corta en el rombo delgado equivale 1:φ φ {displaystyle 1:varphi }, al igual que la relación de los lados a la larga diagonal del grueso rombo. Al igual que con la gatita y el azulejo de dardos, las áreas de estos dos azulejos están en la relación de oro entre sí.
En el dodecaedro y el icosaedro
El dodecaedro regular y su doble poliedro los icosahedro son sólidos platónicos cuyas dimensiones están relacionadas con la relación de oro. Un icosahedro está hecho de 12{displaystyle 12} rostros pentagonales regulares, mientras que el icosahedro está hecho de 20{displaystyle 20} triángulos equiláteros; ambos con 30{displaystyle 30} bordes.
Para un dodecaedro de lado a{displaystyle a}, el radio de una esfera circunscrita e inscrita, y midradius son (ru{displaystyle r_{u}, ri{displaystyle R_{i} y rm{displaystyle R_{m}, respectivamente):
Mientras que para un icosahedro del lado a{displaystyle a}, el radio de una esfera circunscrita e inscrita, y el midradius son:
El volumen y superficie del dodecaedro se pueden expresar en términos de φ φ {displaystyle varphi }:
Además del icosaedro:
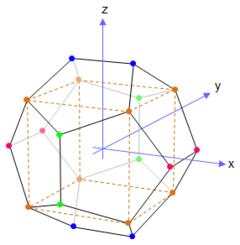
Estos valores geométricos se pueden calcular a partir de sus coordenadas cartesianas, que también se pueden administrar utilizando fórmulas que implican φ φ {displaystyle varphi }. Las coordenadas del dodecaedro se muestran en la figura anterior, mientras que las del icosahedro son las permutaciones cíclicas de:
Conjuntos de tres rectángulos dorados intersecten perpendicularmente dentro de dodecahedra y icosahedra, formando anillos Borromean. En dodecahedra, pares de vértices opuestos en rectángulos dorados encuentran los centros de caras pentagonales, y en icosahedra, se encuentran en sus vértices. En total, los tres rectángulos dorados contienen 12{displaystyle 12} vértices del icosahedro, o equivalentemente, intersectan los centros de 12{displaystyle 12} de las caras del dodecaedro.
Un cubo puede ser inscrito en un dodecaedro regular, con algunas de las diagonales de las caras pentagonales del dodecaedro sirviendo como los bordes del cubo; por lo tanto, las longitudes de los bordes están en la relación de oro. El volumen del cubo es 22+φ φ {displaystyle {tfrac {2}{2+varphi } veces la del dodecaedro. De hecho, los rectángulos dorados dentro de un dodecaedro están en proporciones doradas a un cubo inscrito, tal que los bordes de un cubo y los bordes largos de un rectángulo dorado están en sí mismos φ φ :φ φ 2{displaystyle varphi:varphi ^{2} ratio. Por otro lado, el octaedro, que es el doble poliedro del cubo, puede inscribir un icosahedro, tal que un icosahedro 12{displaystyle 12} vertices tocan 12{displaystyle 12} bordes de un octaedro en puntos que dividen sus bordes en relación dorada.
Otros poliedros están relacionados con el dodecaedro y el icosaedro o sus simetrías y, por lo tanto, tienen relaciones correspondientes con la proporción áurea. Estos incluyen el compuesto de cinco cubos, el compuesto de cinco octaedros, el compuesto de cinco tetraedros, el compuesto de diez tetraedros, el triacontaedro rómbico, el icosidodecaedro, el icosaedro truncado, el dodecaedro truncado y el rombicosidodecaedro, el eneacontaedro rómbico, los poliedros de Kepler-Poinsot y el hexacontaedro rómbico.. En cuatro dimensiones, el dodecaedro y el icosaedro aparecen como caras de las celdas 120 y 600, que nuevamente tienen dimensiones relacionadas con la proporción áurea.
Otras propiedades
La relación de oro decimal expansion se puede calcular mediante métodos de determinación de raíces, como el método de Newton o el método de Halley, en la ecuación x2− − x− − 1=0{displaystyle x^{2}-x-1=0} o en x2− − 5=0{displaystyle x^{2}-5=0} (to compute 5{displaystyle {sqrt {5}} primero). El tiempo necesario para calcular n{displaystyle n} dígitos de la relación de oro usando el método de Newton es esencialmente O()M()n)){displaystyle O(M(n)}, donde M()n){displaystyle M(n)} es la complejidad del tiempo de multiplicar dos n{displaystyle n}- números de dígitos. Esto es considerablemente más rápido que los algoritmos conocidos π π {displaystyle pi} y e{displaystyle e}. Una alternativa programada fácilmente usando sólo aritmética entero es calcular dos grandes números de Fibonacci consecutivos y dividirlos. La relación de los números de Fibonacci F25001{displaystyle F_{25001} y F25000,{displaystyle F_{25000} cada uno 5000{displaystyle 5000} dígitos, rendimientos sobre 10.000.{displaystyle 10{,}000} dígitos significativos de la relación de oro. La expansión decimal de la relación de oro φ φ {displaystyle varphi } se ha calculado a una precisión de diez trillones ()1× × 1013=10,000,000{displaystyle 1times 10^{13}=10{,}000{,}000{,}000{,}000}) dígitos.
La relación dorada y la relación dorada inversa φ φ ± ± =12()1± ± 5){displaystyle varphi _{pm }={tfrac {1}{2}{bigl (}1pm {sqrt {5}{bigr)}}} tienen un conjunto de simetrías que los conservan e interrelacionan. Ambos se conservan por las transformaciones lineales fraccionarias x,1/()1− − x),()x− − 1)/x{displaystyle x,1/(1-x),(x-1)/x} – este hecho corresponde a la identidad y a la ecuación cuadrática de definición.
Además, se intercambian por los tres mapas 1/x,1− − x,x/()x− − 1){displaystyle 1/x,1-x,x/(x-1)} – son recíprocos, simétricos sobre 12,{displaystyle {tfrac}{2}}} y (propuestamente) simétricas 2.{displaystyle 2.} Más profundamente, estos mapas forman un subgrupo del grupo modular PSL ()2,Z){displaystyle operatorname {PSL} (2,mathbb {Z})} isomorfa al grupo simétrico 3{displaystyle 3} letras, S3,{displaystyle S_{3},} correspondiente al estabilizador del conjunto {}0,1,JUEGO JUEGO }{displaystyle {0,1,infty} de 3{displaystyle 3} puntos estándar en la línea de proyecto, y las simetrías corresponden al mapa de referencia S3→ → S2{displaystyle S_{3}to S_{2} – el subgrupo <math alttext="{displaystyle C_{3}C3.S3{displaystyle C_{3}<img alt="C_{3} que consiste en la identidad y la 3{displaystyle 3}- ciclos, en notación de ciclo {}()1),()01JUEGO JUEGO ),()0JUEGO JUEGO 1)},{displaystyle {(1),(0,1,infty),(0,infty ,1)},} fija los dos números, mientras que los 2{displaystyle 2}- ciclos {}()01),()0JUEGO JUEGO ),()1JUEGO JUEGO )}{displaystyle {(0,1),(0,infty),(1,infty)}} intercambiar estos, realizando así el mapa.
En el plano complejo, las quintas raíces de la unidad z=e2π π ki/5{displaystyle z=e^{2pi ki/5} (para un entero) k{textstyle k}) satisfactoria z5=1{displaystyle z^{5}=1} son los vértices de un pentágono. No forman un anillo de enteros cuadráticos, sin embargo la suma de cualquier quinta raíz de la unidad y su complejo conjugado, z+z̄ ̄ ,{displaystyle z+{bar {z}} es un entero cuadrático, un elemento Z[φ φ ].{textstyle mathbb [Z] [varphi]. Específicamente,
Esto también sostiene las décimas raíces restantes de la unidad satisfactoria z10=1,{displaystyle z^{10}=1,}
Para la función gamma .. {displaystyle "Gamma", las únicas soluciones a la ecuación .. ()z− − 1)=.. ()z+1){displaystyle Gamma (z-1)=Gamma (z+1)} son z=φ φ {displaystyle z=varphi } y z=− − φ φ − − 1{displaystyle z=-varphi ^{-1}.
Cuando la relación de oro se utiliza como la base de un sistema numeral (ver la base de la relación de oro, a veces doblada phinary o φ φ {displaystyle varphi }-Nary), enteros cuadráticos en el anillo Z[φ φ ]{displaystyle mathbb {Z} [varphi] – es decir, números de la forma a+bφ φ {displaystyle a+bvarphi } para a,b▪ ▪ Z{displaystyle a,bin mathbb {Z} – han terminado las representaciones, pero las fracciones racionales tienen representaciones no selectivas.
La relación de oro también aparece en la geometría hiperbólica, como la distancia máxima desde un punto en un lado de un triángulo ideal hasta el más cerca de los otros dos lados: esta distancia, la longitud lateral del triángulo equilátero formado por los puntos de la tangencia de un círculo inscrito dentro del triángulo ideal, es 4log ()φ φ ).{displaystyle 4log(varphi).}
La relación de oro aparece también en la teoría de las funciones modulares. Para <math alttext="{displaystyle left|qright|SilencioqSilencio.1{displaystyle left WordPressqright贸n1}<img alt="{displaystyle left|qright|, vamos
Entonces
y
Donde 0}" xmlns="http://www.w3.org/1998/Math/MathML">Im τ τ ■0{displaystyle operatorname {Im}tau }0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e3cbb8e8cc06392e462125f6bbe9c9cfe4906bae" style="vertical-align: -0.338ex; width:8.625ex; height:2.176ex;"/> y ()ez)1/5{displaystyle (e^{z} {1/5} en la fracción continua debe evaluarse como ez/5{displaystyle e^{z/5}. La función τ τ ↦ ↦ R()e2π π iτ τ ){displaystyle tau mapsto R(e^{2pi itau }} es invariable .. ()5){displaystyle Gamma (5)}, un subgrupo de congruencia del grupo modular. También para números reales positivos a,b▪ ▪ R+{displaystyle a,bin mathbb {R} {+} y ab=π π 2,{displaystyle ab=pi ^{2} entonces
y
φ φ {displaystyle varphi } es un número de Pisot-Vijayaraghavan.
Aplicaciones y observaciones
Arquitectura
El arquitecto suizo Le Corbusier, famoso por sus contribuciones al estilo moderno internacional, centró su filosofía de diseño en sistemas de armonía y proporción. La fe de Le Corbusier en el orden matemático del universo estaba estrechamente ligada a la proporción áurea y a la serie de Fibonacci, que describió como "ritmos aparentes a la vista y claros en sus relaciones entre sí". Y estos ritmos están en la raíz misma de las actividades humanas. Resuenan en el hombre por una inevitabilidad orgánica, la misma fina inevitabilidad que hace que los niños, los viejos, los salvajes y los eruditos tracen la Sección Dorada.
Le Corbusier usó explícitamente la proporción áurea en su sistema Modulor para la escala de proporciones arquitectónicas. Vio este sistema como una continuación de la larga tradición de Vitruvio, el 'Hombre de Vitruvio' de Leonardo da Vinci, el trabajo de Leon Battista Alberti y otros que utilizaron las proporciones del cuerpo humano para mejorar la apariencia y función de la arquitectura.
Además de la proporción áurea, Le Corbusier basó el sistema en medidas humanas, números de Fibonacci y la unidad doble. Llevó al extremo la sugerencia de la proporción áurea en proporciones humanas: seccionó la altura del cuerpo humano modelo a la altura del ombligo con las dos secciones en proporción áurea, luego subdividió esas secciones en proporción áurea en las rodillas y la garganta; usó estas proporciones de proporción áurea en el sistema Modulor. La Villa Stein de 1927 de Le Corbusier en Garches ejemplifica la aplicación del sistema Modulor. La planta rectangular, la elevación y la estructura interna de la villa se aproximan mucho a los rectángulos dorados.
Otro arquitecto suizo, Mario Botta, basa muchos de sus diseños en figuras geométricas. Varias casas particulares que diseñó en Suiza se componen de cuadrados y círculos, cubos y cilindros. En una casa que diseñó en Origlio, la proporción áurea es la proporción entre la sección central y las secciones laterales de la casa.
Arte
Las ilustraciones de poliedros de Leonardo da Vinci en la Divinaproporcione de Pacioli han llevado a algunos a especular que incorporó la proporción áurea en sus pinturas. Pero la sugerencia de que su Mona Lisa, por ejemplo, emplea proporciones áureas, no está respaldada por los propios escritos de Leonardo. Del mismo modo, aunque el Hombre de Vitruvio de Leonardo se muestra a menudo en relación con la proporción áurea, las proporciones de la figura en realidad no coinciden y el texto solo menciona proporciones de números enteros.
Salvador Dalí, influenciado por las obras de Matila Ghyka, utilizó explícitamente la proporción áurea en su obra maestra, El Sacramento de la Última Cena. Las dimensiones del lienzo son un rectángulo dorado. Un enorme dodecaedro, en perspectiva de modo que los bordes aparecen en proporción áurea entre sí, está suspendido por encima y detrás de Jesús y domina la composición.
Un estudio estadístico sobre 565 obras de arte de diferentes grandes pintores, realizado en 1999, encontró que estos artistas no habían utilizado la relación de oro en el tamaño de sus lienzos. El estudio concluyó que la relación media de los dos lados de las pinturas estudiadas es 1.34,{displaystyle 1.34,} con promedios para artistas individuales que van desde 1.04{displaystyle 1.04} (Goya) a 1.46{displaystyle 1.46} (Bellini). Por otro lado, Pablo Tosto enumera más de 350 obras de artistas conocidos, incluyendo más de 100 que tienen lienzos con rectángulo dorado y 5{displaystyle {sqrt {5}} proporciones, y otros con proporciones como 2,{displaystyle {sqrt {2}} 3,{displaystyle 3,} 4,{displaystyle 4,} y 6.{displaystyle 6.}
Libros y diseño
Según Jan Tschichold,
Hubo un tiempo en que las desviaciones de las proporciones de página verdaderamente hermosas 2:3,{displaystyle 2mathbin {:} 3,} 1:3,{displaystyle 1mathbin {} {sqrt {3}}} y la Sección de Oro eran raras. Muchos libros producidos entre 1550 y 1770 muestran estas proporciones exactamente, hasta dentro de medio milímetro.
Según algunas fuentes, la proporción áurea se utiliza en el diseño cotidiano, por ejemplo, en las proporciones de naipes, postales, carteles, placas de interruptores de luz y televisores de pantalla ancha.
Banderas
Se pretendía que la relación de aspecto (relación ancho/alto) de la bandera de Togo fuera la proporción áurea, según su diseñador.
Música
Ernő Lendvai analiza las obras de Béla Bartók como basadas en dos sistemas opuestos, el de la proporción áurea y la escala acústica, aunque otros estudiosos de la música rechazan ese análisis. El compositor francés Erik Satie utilizó la proporción áurea en varias de sus piezas, incluidas Sonneries de la Rose+Croix. La proporción áurea también es evidente en la organización de las secciones en la música de Reflets dans l'eau (Reflejos en el agua) de Debussy, de Images (1.ª serie, 1905), en la que "la secuencia de teclas está marcada por los intervalos 34, 21, 13 y 8, y el clímax principal se encuentra en la posición phi".
El musicólogo Roy Howat ha observado que los límites formales de La Mer de Debussy corresponden exactamente a la sección áurea. Trezise encuentra la evidencia intrínseca 'notable', pero advierte que ninguna evidencia escrita o reportada sugiere que Debussy buscó conscientemente tales proporciones.
Teóricos musicales como Hans Zender y Heinz Bohlen han experimentado con la escala de 833 centavos, una escala musical basada en el uso de la proporción áurea como su intervalo musical fundamental. Cuando se mide en centavos, una escala logarítmica para intervalos musicales, la proporción áurea es de aproximadamente 833,09 centavos.
Naturaleza
Johannes Kepler escribió que "la imagen del hombre y la mujer proviene de la proporción divina. En mi opinión, la propagación de las plantas y los actos progenitores de los animales están en la misma proporción.
El psicólogo Adolf Zeising señaló que la proporción áurea aparecía en la filotaxis y argumentó a partir de estos patrones en la naturaleza que la proporción áurea era una ley universal. Zeising escribió en 1854 sobre una ley ortogenética universal de "luchar por la belleza y la integridad en los reinos de la naturaleza y el arte".
Sin embargo, algunos han argumentado que muchas manifestaciones aparentes de la proporción áurea en la naturaleza, especialmente en lo que respecta a las dimensiones de los animales, son ficticias.
Física
El ferroimán de Ising casi unidimensional CoNb2O6 (niobato de cobalto) tiene 8 estados de excitación predichos (con simetría E8), que cuando se prueba con dispersión de neutrones, mostró que sus dos más bajos estaban en proporción áurea. Específicamente, estas transiciones de fase cuántica durante la excitación de espín, que ocurren a una temperatura cercana al cero absoluto, mostraron pares de torceduras en su fase ordenada a giros de espín en su fase paramagnética; revelando, justo debajo de su campo crítico, una dinámica de giro con modos agudos a bajas energías que se acercan a la media dorada.
Optimización
No hay ningún algoritmo general conocido para organizar un número determinado de nodos uniformemente en una esfera, para cualquiera de las definiciones de distribución uniforme (véase, por ejemplo, Thomson problem o Problema de Tammes). Sin embargo, una aproximación útil resulta de dividir la esfera en bandas paralelas de superficie igual y colocar un nodo en cada banda en longitudes espaciadas por una sección dorada del círculo, es decir. 360∘ ∘ /φ φ .. 222.5∘ ∘ .{displaystyle 360^{circ }/varphi approx 222.5^{circ } Este método se utilizó para organizar los 1500 espejos del satélite participante estudiantil Starshine-3.
La proporción áurea también es un elemento fundamental para la búsqueda de la sección áurea.
Observaciones disputadas
Ejemplos de observaciones cuestionadas de la proporción áurea incluyen los siguientes:
- Algunas proporciones específicas en los cuerpos de muchos animales (incluidos los humanos) y partes de las cáscaras de moluscos se afirman a menudo estar en la relación de oro. Hay una gran variación en las medidas reales de estos elementos en individuos específicos, sin embargo, y la proporción en cuestión es a menudo significativamente diferente de la relación de oro. Se ha dicho que la relación de los huesos de los dígitos y el hueso metacarpiano es aproximada a la relación de oro. La cáscara nautilus, cuya construcción procede en una espiral logarítmica, se cita a menudo, generalmente con la idea errónea de que cualquier espiral logarítmica está relacionada con la relación de oro, pero a veces con la afirmación de que cada nueva cámara es dorada-proporcionada relativa a la anterior. However, measurements of nautilus shells do not support this claim.
- Historiador John El hombre afirma que tanto las páginas como el área de texto de la Biblia Gutenberg fueron "basados en la forma de la sección dorada". Sin embargo, según sus propias medidas, la relación de altura a ancho de las páginas es 1.45.{displaystyle 1.45.}
- Estudios de psicólogos, comenzando por Gustav Fechner c. 1876, han sido ideados para probar la idea de que la relación de oro juega un papel en la percepción humana de la belleza. Mientras Fechner encontró una preferencia por las ratios rectángulos centradas en la relación de oro, intentos posteriores de probar cuidadosamente tal hipótesis han sido, en el mejor de los casos, inconclusivas.
- En la inversión, algunos profesionales del análisis técnico utilizan la relación de oro para indicar el apoyo a un nivel de precio, o la resistencia a los aumentos de precios, de una acción o mercancía; después de cambios significativos de precio arriba o abajo, se supone que se encuentran nuevos niveles de apoyo y resistencia a precios cercanos relacionados con el precio inicial a través de la relación de oro. El uso de la relación de oro en la inversión también está relacionado con patrones más complicados descritos por los números Fibonacci (por ejemplo, el principio de onda Elliott y el retracemento Fibonacci). Sin embargo, otros analistas de mercado han publicado análisis que sugieren que estos porcentajes y patrones no están respaldados por los datos.
Pirámides de Egipto
Los piramidólogos han analizado que la Gran Pirámide de Giza (también conocida como la Pirámide de Keops o Khufu) tiene un triángulo de Kepler duplicado como sección transversal. Si esta teoría fuera cierta, la proporción áurea describiría la proporción de distancias desde el punto medio de uno de los lados de la pirámide hasta su vértice, y desde el mismo punto medio hasta el centro de la base de la pirámide. Sin embargo, la imprecisión en la medición causada en parte por la remoción de la superficie exterior de la pirámide hace imposible distinguir esta teoría de otras teorías numéricas de las proporciones de la pirámide, basadas en pi o en proporciones de números enteros. El consenso de los eruditos modernos es que las proporciones de esta pirámide no se basan en la proporción áurea, porque tal base sería inconsistente tanto con lo que se sabe sobre las matemáticas egipcias desde la época de la construcción de la pirámide como con las teorías egipcias. de arquitectura y proporción utilizados en sus otras obras.
El Partenón
Algunos dicen que la fachada del Partenón (c. 432 a. C.), así como los elementos de su fachada y otros lugares, están circunscritos por rectángulos dorados. Otros estudiosos niegan que los griegos tuvieran alguna asociación estética con la proporción áurea. Por ejemplo, Keith Devlin dice: 'Ciertamente, la afirmación tan repetida de que el Partenón de Atenas se basa en la proporción áurea no está respaldada por medidas reales. De hecho, toda la historia sobre los griegos y la proporción áurea parece carecer de fundamento." Midhat J. Gazalé afirma que "No fue hasta Euclides... que se estudiaron las propiedades matemáticas de la proporción áurea."
A partir de las mediciones de 15 templos, 18 tumbas monumentales, 8 sarcófagos y 58 estelas funerarias desde el siglo V a. C. hasta el siglo II d. C., un investigador concluyó que la proporción áurea estaba totalmente ausente en la arquitectura griega del siglo V clásico a., y casi ausente durante los siguientes seis siglos. Fuentes posteriores como Vitruvio (siglo I a. C.) hablan exclusivamente de proporciones que se pueden expresar en números enteros, es decir, proporciones conmensurables en lugar de irracionales.
Arte moderno
La Section d'Or ('Sección Dorada') fue un colectivo de pintores, escultores, poetas y críticos asociados con el cubismo y el orfismo. Activos desde 1911 hasta alrededor de 1914, adoptaron el nombre tanto para resaltar que el cubismo representaba la continuación de una gran tradición, en lugar de ser un movimiento aislado, como en homenaje a la armonía matemática asociada con Georges Seurat. (Varios autores han afirmado que Seurat empleó la proporción áurea en sus pinturas, pero los escritos y pinturas de Seurat sugieren que empleó proporciones simples de números enteros y que cualquier aproximación a la proporción áurea fue una coincidencia). Los cubistas observaron en sus armonías, la estructuración geométrica de movimiento y forma, "la primacía de la idea sobre la naturaleza", "una absoluta claridad científica de concepción". Sin embargo, a pesar de este interés general en la armonía matemática, es más difícil determinar si las pinturas presentadas en la célebre exposición Salon de la Section d'Or de 1912 utilizaron la proporción áurea en alguna composición. Livio, por ejemplo, afirma que no, y Marcel Duchamp lo dijo en una entrevista. Por otro lado, un análisis sugiere que Juan Gris hizo uso de la proporción áurea en la composición de obras que probablemente, pero no definitivamente, se exhibieron en la exposición. El historiador de arte Daniel Robbins ha argumentado que además de hacer referencia al término matemático, el nombre de la exposición también se refiere al anterior grupo Bandeaux d'Or, con el que Albert Gleizes y otros ex miembros de la Abbaye de Créteil había estado involucrada.
Se dice que Piet Mondrian usó la sección áurea ampliamente en sus pinturas geométricas, aunque otros expertos (incluido el crítico Yve-Alain Bois) han desacreditado estas afirmaciones.
Contenido relacionado
Problema de correspondencia postal
Íntimo y supremo
Funcion exponencial












































![{displaystyle {begin{aligned}varphi ^{2}&=varphi +1=2.618033dots\[5mu]{frac {1}{varphi }}&=varphi -1=0.618033dots.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2e5225abf67548cf93c882add3a4b439c4aeb8)






![{displaystyle {begin{aligned}varphi ^{n}&=varphi ^{n-1}+varphi ^{n-3}+cdots +varphi ^{n-1-2m}+varphi ^{n-2-2m}\[5mu]varphi ^{n}-varphi ^{n-1}&=varphi ^{n-2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048f09b7012c7fbd3d9f32798de6dd5c01acabcd)


![varphi =[1;1,1,1,dots ]=1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95682588ffee3530627c3a7b00ff08bbba6e97d4)
![varphi ^{-1}=[0;1,1,1,dots ]=0+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/165d255e32f4b9af1f9144f15302b147fc3fead2)

















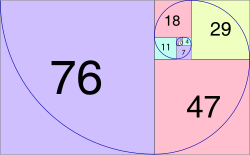








































![{displaystyle {begin{aligned}3varphi ^{3}-5varphi ^{2}+4&=3(varphi ^{2}+varphi)-5varphi ^{2}+4\[5mu]&=3[(varphi +1)+varphi ]-5(varphi +1)+4\[5mu]&=varphi +2approx 3.618033.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60ff8508aa117064d60142d447fb0cb58a809848)


![{displaystyle {begin{aligned}varphi ^{0}&=1,\[5mu]varphi ^{1}&=1.618033989...approx 2,\[5mu]varphi ^{2}&=2.618033989...approx 3,\[5mu]varphi ^{3}&=4.236067978...approx 4,\[5mu]varphi ^{4}&=6.854101967...approx 7,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c9bfd2f9bdc877282b290adc74c88f1dfa63c8)































![{displaystyle {begin{aligned}{frac {2pi -g}{g}}&={frac {2pi }{2pi -g}}=varphi\[8mu]2pi -g&={frac {2pi }{varphi }}approx 222.5^{circ },\[8mu]g&={frac {2pi }{varphi ^{2}}}approx 137.5^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5f9122b38d09e0cd2992820f27b8587efd167a)






















![{displaystyle {begin{aligned}A&={tfrac {s^{2}}{2}}{sqrt {varphi }},\[5mu]theta &=sin ^{-1}{frac {1}{varphi }}approx 38.1727^{circ },\[5mu]theta &=cos ^{-1}{frac {1}{varphi }}approx 51.8273^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96fa323a2e180a6198f05d33c13e1631854e840)



















![{displaystyle {begin{aligned}alpha &=2arctan {1 over varphi }approx 63.43495^{circ },\[5mu]beta &=2arctan varphi =pi -arctan 2=arctan 1+arctan 3approx 116.56505^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c5a4321454f4ca1b41b0dbd8f2c6c4afd48467e)


![{displaystyle {begin{aligned}d&={2a over {sqrt {2+varphi }}}=2{sqrt {{3-varphi } over 5}}aapprox 1.05146a,\[5mu]D&=2{sqrt {{2+varphi } over 5}}aapprox 1.70130a.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00bbc42679ab9e34fdf849ac68de75180cc92c7)
![{displaystyle {begin{aligned}A&=(sin(arctan 2))~a^{2}={2 over {sqrt {5}}}~a^{2}approx 0.89443a^{2},\[5mu]A&={{varphi } over 2}d^{2}approx 0.80902d^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bed70dcf23f16f3f8241aeaf2b56f0897244ff3)






![{displaystyle {begin{aligned}varphi &=1+2sin(pi /10)=1+2sin 18^{circ },\[5mu]varphi &={tfrac {1}{2}}csc(pi /10)={tfrac {1}{2}}csc 18^{circ },\[5mu]varphi &=2cos(pi /5)=2cos 36^{circ },\[5mu]varphi &=2sin(3pi /10)=2sin 54^{circ }.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c42bbf25d6257a00fad895691aa2c5eb0c6f57a)



















































![{textstyle mathbb {Z} [varphi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c19ab3d8278828be7f591bad1dc4482e4aaac6d)
![{displaystyle {begin{aligned}e^{0}+e^{-0}&=2,\[5mu]e^{2pi i/5}+e^{-2pi i/5}&=varphi ^{-1}=-1+varphi\[5mu]e^{4pi i/5}+e^{-4pi i/5}&=-varphi.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec7bcbd2e99aef0874eb163966c3e2dd9424b86)

![{displaystyle {begin{aligned}e^{pi i}+e^{-pi i}&=-2,\[5mu]e^{pi i/5}+e^{-pi i/5}&=varphi\[5mu]e^{3pi i/5}+e^{-3pi i/5}&=-varphi ^{-1}=1-varphi.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9459634b32b6990a97eb560ce696a3bc2e722513)




![{displaystyle mathbb {Z} [varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201)