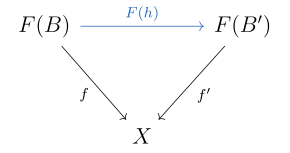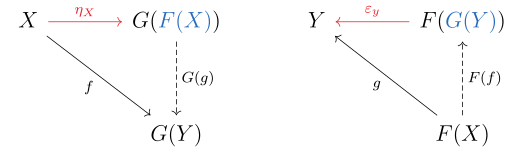Propiedad universal

El diagrama típico de la definición de morfismo universal.

En matemáticas, más concretamente en teoría de categorías, una propiedad universal es una propiedad que caracteriza hasta un isomorfismo el resultado de algunas construcciones. Así, las propiedades universales pueden usarse para definir algunos objetos independientemente del método elegido para construirlos. Por ejemplo, las definiciones de los números enteros a partir de los números naturales, de los números racionales a partir de los números enteros, de los números reales a partir de los números racionales, y de los anillos polinómicos a partir del campo de sus coeficientes, pueden hacerse en términos de propiedades universales. En particular, el concepto de propiedad universal permite una demostración simple de que todas las construcciones de los números reales son equivalentes: basta probar que satisfacen la misma propiedad universal.

Técnicamente, una propiedad universal se define en términos de categorías y funtores por medio de un morfismo universal (ver § Definición formal, a continuación). Los morfismos universales también se pueden pensar de manera más abstracta como objetos iniciales o terminales de una categoría de coma (ver § Conexión con categorías de coma, a continuación).

Las propiedades universales ocurren casi en todas partes en las matemáticas, y el uso del concepto permite el uso de propiedades generales de propiedades universales para probar fácilmente algunas propiedades que necesitarían verificaciones aburridas de otra manera. Por ejemplo, dado un anillo conmutativo R, el campo de las fracciones del anillo cociente de R por un ideal primo p se puede identificar con el campo de residuos de la localización R a p; eso es ${displaystyle R_{p}/pR_{p}cong operatorname {Frac} (R/p)}$ (todas estas construcciones se pueden definir por propiedades universales).

Otros objetos que se pueden definir mediante propiedades universales incluyen: todos los objetos libres, productos directos y sumas directas, grupos libres, celosías libres, grupo de Grothendieck, finalización de un espacio métrico, finalización de un anillo, finalización de Dedekind-MacNeille, producto topologías, compactación de Stone-Čech, productos tensoriales, límite inverso y límite directo, núcleos y conúcleos, grupos de cocientes, espacios vectoriales de cocientes y otros espacios de cocientes.

Motivación

Antes de dar una definición formal de propiedades universales, ofrecemos algunas motivaciones para estudiar tales construcciones.

• Los detalles concretos de una construcción dada pueden ser desordenados, pero si la construcción satisface una propiedad universal, se puede olvidar todos esos detalles: todo lo que hay que saber sobre la construcción ya está contenido en la propiedad universal. Las pruebas a menudo se vuelven cortas y elegantes si la propiedad universal se utiliza en lugar de los detalles concretos. Por ejemplo, el álgebra tensor de un espacio vectorial es ligeramente complicado de construir, pero mucho más fácil de tratar por su propiedad universal.
• Las propiedades universales definen objetos únicamente hasta un isomorfismo único. Por lo tanto, una estrategia para probar que dos objetos son isomorfos es demostrar que satisfacen la misma propiedad universal.
• Las construcciones universales son functoriales en la naturaleza: si se puede realizar la construcción de cada objeto en una categoría C entonces uno obtiene un functor en C. Además, este functor es una unión derecha o izquierda al functor U utilizado en la definición de la propiedad universal.
• Las propiedades universales ocurren en todas partes en las matemáticas. Al comprender sus propiedades abstractas, uno obtiene información sobre todas estas construcciones y puede evitar repetir el mismo análisis para cada instancia individual.

Definición formal

Para entender la definición de una construcción universal, es importante mirar ejemplos. Las construcciones universales no se definieron de la nada, sino que se definieron después de que los matemáticos comenzaron a notar un patrón en muchas construcciones matemáticas (consulte los ejemplos a continuación). Por lo tanto, la definición puede no tener sentido para uno al principio, pero se aclarará cuando uno la reconcilie con ejemplos concretos.

Vamos ${displaystyle F:{mathcal {C}to {fnMithcal} {}}$ ser un functor entre categorías ${displaystyle {fnMithcal}}$ y ${displaystyle {fnMithcal}}$. En lo que sigue, dejemos ${displaystyle X}$ ser un objeto de ${displaystyle {fnMithcal}}$, mientras ${displaystyle A}$ y ${displaystyle A'$ son objetos de ${displaystyle {fnMithcal}}$, y ${displaystyle h}$ es un morfismo en ${displaystyle {fnMithcal}}$.

Así, el functor ${displaystyle F}$ mapas ${displaystyle A}$, ${displaystyle A'$ y ${displaystyle h}$ dentro ${displaystyle {fnMithcal}}$ a ${displaystyle F(A)}$, ${displaystyle F(A)}$ y ${displaystyle F(h)}$ dentro ${displaystyle {fnMithcal}}$.

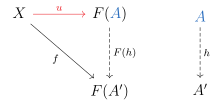
A morfismo universal ${displaystyle X}$ a ${displaystyle F}$ es un par único ${displaystyle (A,u:Xto F(A)}$ dentro ${displaystyle {fnMithcal}}$ que tiene la propiedad siguiente, comúnmente conocida como propiedad universal:

Para cualquier morfismo de la forma ${displaystyle f:Xto F(A)}$ dentro ${displaystyle {fnMithcal}}$, existe un único morfismo ${displaystyle h:Ato A}$ dentro ${displaystyle {fnMithcal}}$ tal que el siguiente diagrama comunique:

Podemos dualizar este concepto categórico. A morfismo universal ${displaystyle F}$ a ${displaystyle X}$ es un par único ${displaystyle (A,u:F(A)to X)}$ que satisface la siguiente propiedad universal:

Para cualquier morfismo de la forma ${displaystyle f:F(A)to X}$ dentro ${displaystyle {fnMithcal}}$, existe un único morfismo ${displaystyle h:A'to A}$ dentro ${displaystyle {fnMithcal}}$ tal que el siguiente diagrama comunique:

Tenga en cuenta que en cada definición, las flechas se revierten. Ambas definiciones son necesarias para describir construcciones universales que aparecen en matemáticas; pero también surgen debido a la dualidad inherente presente en la teoría de la categoría. En cualquier caso, decimos que el par ${displaystyle (A,u)}$ que se comporta como arriba satisface una propiedad universal.

Conexión con categorías de coma

Los morfismos universales se pueden describir de manera más concisa como objetos iniciales y terminales en una categoría de coma (es decir, una en la que los morfismos se ven como objetos por derecho propio).

Vamos ${displaystyle F:{mathcal {C}to {fnMithcal} {}}$ ser un functor y ${displaystyle X}$ un objeto de ${displaystyle {fnMithcal}}$. Entonces recuerde que la categoría de coma ${displaystyle (Xdownarrow F)}$ es la categoría donde

• Los objetos son pares de la forma ${displaystyle (B,f:Xto F(B)}$, donde ${displaystyle B}$ es un objeto en ${displaystyle {fnMithcal}}$
• Un morfismo de ${displaystyle (B,f:Xto F(B)}$ a ${displaystyle (B',f':Xto F(B')}$ es dado por un morfismo ${displaystyle h:Bto B}$ dentro ${displaystyle {fnMithcal}}$ tal que el diagrama conmuta:

Ahora supongamos que el objeto ${displaystyle (A,u:Xto F(A)}$ dentro ${displaystyle (Xdownarrow F)}$ es inicial. Entonces... para cada objeto ${displaystyle (A',f:Xto F(A')}$, existe un morfismo único ${displaystyle h:Ato A}$ tal que el siguiente diagrama comunique.

Tenga en cuenta que la igualdad aquí simplemente significa que los diagramas son los mismos. También tenga en cuenta que el diagrama en el lado derecho de la igualdad es el mismo que el que se ofrece en la definición de un morfismo universal ${displaystyle X}$ a ${displaystyle F}$. Por lo tanto, vemos que un morfismo universal ${displaystyle X}$ a ${displaystyle F}$ es equivalente a un objeto inicial en la categoría de coma ${displaystyle (Xdownarrow F)}$.

Por el contrario, recuerde que la categoría de coma ${displaystyle (Fdownarrow X)}$ es la categoría donde

• Los objetos son pares de la forma ${displaystyle (B,f:F(B)to X)}$ Donde ${displaystyle B}$ es un objeto en ${displaystyle {fnMithcal}}$
• Un morfismo de ${displaystyle (B,f:F(B)to X)}$ a ${displaystyle (B',f':F(B')to X)}$ es dado por un morfismo ${displaystyle h:Bto B}$ dentro ${displaystyle {fnMithcal}}$ tal que el diagrama conmuta:

Suppose ${displaystyle (A,u:F(A)to X)}$ es un objeto terminal en ${displaystyle (Fdownarrow X)}$. Entonces por cada objeto ${displaystyle (A',f:F(A')to X)}$, existe un morfismo único ${displaystyle h:A'to A}$ tal que los siguientes diagramas comuniquen.

El diagrama en el lado derecho de la igualdad es el mismo diagrama ilustrado al definir un morfismo universal ${displaystyle F}$ a ${displaystyle X}$. Por lo tanto, un morfismo universal de ${displaystyle F}$ a ${displaystyle X}$ corresponde con un objeto terminal en la categoría de coma ${displaystyle (Fdownarrow X)}$.

Ejemplos

A continuación se muestran algunos ejemplos para resaltar la idea general. El lector puede construir muchos otros ejemplos consultando los artículos mencionados en la introducción.

Álgebra tensorial

Vamos ${displaystyle {fnMithcal}}$ ser la categoría de espacios vectoriales ${displaystyle K}$-Vect. sobre un terreno ${displaystyle K}$ y dejar ${displaystyle {fnMithcal}}$ ser la categoría de álgebras ${displaystyle K}$-Alg sobre ${displaystyle K}$ (según sea unitario y asociativo). Vamos

${displaystyle U}$: ${displaystyle K}$-Alg → ${displaystyle K}$-Vect.

sea el funtor olvidadizo que asigna a cada álgebra su espacio vectorial subyacente.

Dado cualquier espacio vectorial ${displaystyle V}$ sobre ${displaystyle K}$ podemos construir el álgebra tensor ${displaystyle T(V)}$. El álgebra tensor se caracteriza por el hecho:

“Cualquier mapa lineal de ${displaystyle V}$ a un álgebra ${displaystyle A}$ se puede extender únicamente a un homomorfismo álgebra de ${displaystyle T(V)}$ a ${displaystyle A}$.

Esta declaración es una propiedad inicial del álgebra tensor ya que expresa el hecho de que el par ${displaystyle (T(V),i)}$, donde ${displaystyle i:Vto U(T(V)}$ es el mapa de inclusión, es un morfismo universal del espacio vectorial ${displaystyle V}$ al functor ${displaystyle U}$.

Desde esta construcción funciona para cualquier espacio vectorial ${displaystyle V}$, concluimos que ${displaystyle T}$ es un functor de ${displaystyle K}$-Vect. a ${displaystyle K}$-Alg. Esto significa que ${displaystyle T}$ es izquierda al funerario olvidadizo ${displaystyle U}$ (ver la sección siguiente en relación con los functores adjuntos).

Productos

Un producto categórico se puede caracterizar por una construcción universal. Para concretar, uno puede considerar el producto cartesiano en Set, el producto directo en Grp, o la topología del producto en Top, donde existen productos.

Vamos ${displaystyle X}$ y ${displaystyle Sí.$ ser objetos de una categoría ${displaystyle {fnMithcal}}$ con productos finitos. El producto de ${displaystyle X}$ y ${displaystyle Sí.$ es un objeto ${displaystyle X}$ × ${displaystyle Sí.$ junto con dos morfismos

${displaystyle pi ¿Qué?$: ${displaystyle Xtimes Yto X}$

${displaystyle pi _{2}$: ${displaystyle Xtimes Yto Sí.$

tal que para cualquier otro objeto ${displaystyle Z}$ de ${displaystyle {fnMithcal}}$ y morfismos ${displaystyle f:Zto X}$ y ${displaystyle g:Zto Y}$ existe un morfismo único ${displaystyle h:Zto Xtimes Y}$ tales que ${displaystyle f=pi _{1}circ h}$ y ${displaystyle g=pi ¿Qué? h)$.

Para entender esta caracterización como una propiedad universal, tome la categoría ${displaystyle {fnMithcal}}$ categoría de productos ${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$ y definir el functor diagonal

${displaystyle "Delta:{mathcal {C}to {mathcal {C}times {mathcal {C}}$

por ${displaystyle Delta (X)=(X,X)}$ y ${displaystyle Delta (f:Xto Y)=(f,f)}$. Entonces... ${displaystyle (Xtimes Y,(pi _{1},pi _{2})}$ es un morfismo universal ${displaystyle Delta }$ al objeto ${displaystyle (X,Y)}$ de ${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$Si ${displaystyle (f,g)}$ es cualquier morfismo de ${displaystyle (Z,Z)}$ a ${displaystyle (X,Y)}$, entonces debe igual un morfismo ${displaystyle Delta (h:Zto Xtimes Y)=(h,h)}$ desde ${displaystyle Delta (Z)=(Z,Z)}$a ${displaystyle Delta (Xtimes Y)=(Xtimes Y,Xtimes Y)}$ seguido ${displaystyle (pi _{1},pi _{2}}$.

Límites y colímites

Los productos categóricos son un tipo particular de límite en la teoría de categorías. Se puede generalizar el ejemplo anterior a límites y colimits arbitrarios.

Vamos ${displaystyle {fnMithcal}}$ y ${displaystyle {fnMithcal}}$ categorías con ${displaystyle {fnMithcal}}$ una pequeña categoría de índice y dejar ${displaystyle {fnMitcal} {fnMitcal} {fnMitcal} {fnMitcal}}} {fnMitcal}} {fnMitcal {J}}$ ser la categoría functor correspondiente. El functor diagonal

${displaystyle Delta: {fnMitcal {fnMitcal} {fnMitcal} {fnMitcal} {cHFF} {J}}$

es el functor que mapea cada objeto ${displaystyle N}$ dentro ${displaystyle {fnMithcal}}$ al functor constante ${displaystyle Delta (N):{mathcal {J}to {mathcal {C}}$ a ${displaystyle N}$ (i.e. ${displaystyle Delta (N)(X)=N}$ para cada uno ${displaystyle X}$ dentro ${displaystyle {fnMithcal}}$).

Dado un functor ${displaystyle F:{mathcal {J}to {Mathcal {C}}$ (pensamiento de como objeto en ${displaystyle {fnMitcal} {fnMitcal} {fnMitcal} {fnMitcal}}} {fnMitcal}} {fnMitcal {J}}$), el límite de ${displaystyle F}$, si existe, no es más que un morfismo universal ${displaystyle Delta }$ a ${displaystyle F}$. Dualmente, el colimit de ${displaystyle F}$ es un morfismo universal ${displaystyle F}$ a ${displaystyle Delta }$.

Propiedades

Existencia y unicidad

Definir una cantidad no garantiza su existencia. Dado un functor ${displaystyle F:{mathcal {C}to {fnMithcal} {}}$ y un objeto ${displaystyle X}$ de ${displaystyle {fnMithcal}}$, puede existir o no un morfismo universal ${displaystyle X}$ a ${displaystyle F}$. Si, sin embargo, un morfismo universal ${displaystyle (A,u)}$ existe, entonces es esencialmente único. Específicamente, es único hasta un único isomorfismo: si ${displaystyle (A',u')}$ es otro par, entonces existe un isomorfismo único ${displaystyle k:Ato A}$ tales que ${displaystyle u'=F(k)circ u}$. Esto se ve fácilmente por sustitución ${displaystyle (A,u')}$ en la definición de un morfismo universal.

Es el par ${displaystyle (A,u)}$ que es esencialmente único en esta moda. El objeto ${displaystyle A}$ en sí solo es único hasta el isomorfismo. De hecho, si ${displaystyle (A,u)}$ es un morfismo universal y ${displaystyle k:Ato A}$ es cualquier isomorfismo entonces el par ${displaystyle (A',u')}$, donde ${displaystyle u'=F(k)circ u}$ es también un morfismo universal.

Formulaciones equivalentes

La definición de morfismo universal puede reformularse de diversas maneras. Vamos ${displaystyle F:{mathcal {C}to {fnMithcal} {}}$ ser un functor y dejar ${displaystyle X}$ ser un objeto de ${displaystyle {fnMithcal}}$. Entonces las siguientes declaraciones son equivalentes:

• ${displaystyle (A,u)}$ es un morfismo universal ${displaystyle X}$ a ${displaystyle F}$
• ${displaystyle (A,u)}$ es un objeto inicial de la categoría de coma ${displaystyle (Xdownarrow F)}$
• ${displaystyle (A,u)}$ es una representación de ${displaystyle {text{Hom}_{mathcal {}(X,F(-)}$

Las declaraciones duales también son equivalentes:

• ${displaystyle (A,u)}$ es un morfismo universal ${displaystyle F}$ a ${displaystyle X}$
• ${displaystyle (A,u)}$ es un objeto terminal de la categoría de coma ${displaystyle (Fdownarrow X)}$
• ${displaystyle (A,u)}$ es una representación de ${displaystyle {text{Hom}_{mathcal {}(F(-),X)}$

Relación con los funtores adjuntos

Suppose ${displaystyle (A_{1},u_{1})}$ es un morfismo universal ${displaystyle X_{1}$ a ${displaystyle F}$ y ${displaystyle (A_{2},u_{2}}$ es un morfismo universal ${displaystyle X_{2}$ a ${displaystyle F}$. Por la propiedad universal de los morfismos universales, dada cualquier morfismo ${displaystyle h:X_{1}to X_{2}$ existe un morfismo único ${displaystyle g:A_{1}to A_{2}$ tal que el siguiente diagrama comunique:

Si cada uno objeto ${displaystyle X_{i}$ de ${displaystyle {fnMithcal}}$ admite un morfismo universal ${displaystyle F}$, entonces la asignación ${displaystyle X_{i}mapsto A_{i}$ y ${displaystyle hmapsto g}$ define un functor ${displaystyle G: {fnMithcal {}to {fnMithcal {C}}$. Los mapas ${displaystyle U_{i}$ entonces definir una transformación natural de ${displaystyle 1_{Mathcal {}}$ (el functor de identidad en ${displaystyle {fnMithcal}}$) a ${displaystyle Fcirc G}$. Los functores ${displaystyle (F,G)}$ son entonces un par de funerarios adjuntos, con ${displaystyle G.$ izquierda-adjoint ${displaystyle F}$ y ${displaystyle F}$ derecho a ${displaystyle G.$.

Declaraciones similares se aplican a la doble situación de los morfismos terminales de ${displaystyle F}$. Si tales morfismos existen para cada ${displaystyle X}$ dentro ${displaystyle {fnMithcal}}$ uno obtiene un functor ${displaystyle G:{mathcal {C} {fn} {fnMitcal {}}} {fnK}} {fnK}} {fn}} {fn}}}} {fn}}} {fn}}}} {fn}} {\\fn} {\\fnH}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$ que es la unión correcta ${displaystyle F}$ (so ${displaystyle F}$ es zurdo ${displaystyle G.$).

De hecho, todos los pares de functores unidos surgen de construcciones universales de esta manera. Vamos ${displaystyle F}$ y ${displaystyle G.$ ser un par de functores adjuntos con unidad ${displaystyle eta }$ y co-unidad ${displaystyle epsilon }$ (ver el artículo sobre functores adjuntos para las definiciones). Entonces tenemos un morfismo universal para cada objeto en ${displaystyle {fnMithcal}}$ y ${displaystyle {fnMithcal}}$:

• Para cada objeto ${displaystyle X}$ dentro ${displaystyle {fnMithcal}}$, ${displaystyle (F(X),eta ¿Qué?$ es un morfismo universal ${displaystyle X}$ a ${displaystyle G.$. Eso es, para todos ${displaystyle f:Xto G(Y)}$ existe una ${displaystyle g:F(X)to Sí.$ para los cuales se comunican los siguientes diagramas.
• Para cada objeto ${displaystyle Sí.$ dentro ${displaystyle {fnMithcal}}$, ${displaystyle (G(Y),epsilon _{Y})}$ es un morfismo universal ${displaystyle F}$ a ${displaystyle Sí.$. Eso es, para todos ${displaystyle g:F(X)to Sí.$ existe una ${displaystyle f:Xto G(Y)}$ para los cuales se comunican los siguientes diagramas.

Las construcciones universales son más generales que los pares de functores adjuntos: una construcción universal es como un problema de optimización; da lugar a un par adyacente si y sólo si este problema tiene una solución para cada objeto de ${displaystyle {fnMithcal}}$ (equivalentemente, cada objeto de ${displaystyle {fnMithcal}}$).

Historia

Pierre Samuel presentó las propiedades universales de varias construcciones topológicas en 1948. Más tarde, Bourbaki las utilizó ampliamente. El concepto estrechamente relacionado de funtores adjuntos fue introducido de forma independiente por Daniel Kan en 1958.