Producto cruzado

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Operación matemática en vectores en espacio 3D

En matemáticas, la producto cruzado o producto vectorial (ocasionalmente) producto de área dirigida, para enfatizar su significado geométrico) es una operación binaria en dos vectores en un espacio vectorial Euclideano orientado tridimensional (llamado aquí $E$ ), y es denotado por el símbolo $times$ . Dados dos vectores linealmente independientes $a$ y $b$ , el producto de la cruz, $a \times b$ (read "a cross b"), es un vector perpendicular a ambos $a$ y $b$ , y por lo tanto normal al plano que los contiene. Tiene muchas aplicaciones en matemáticas, física, ingeniería y programación informática. No debe confundirse con el producto de puntos (producto de proyección).

Si dos vectores tienen la misma dirección o tienen direcciones exactamente opuestas entre sí (es decir, no son no linealmente independientes), o si cualquiera de ellos tiene longitud cero, entonces su producto vectorial es cero. Más generalmente, la magnitud del producto es igual al área de un paralelogramo con los vectores de los lados; en particular, la magnitud del producto de dos vectores perpendiculares es el producto de sus longitudes.

El producto cruzado es anticommutante (es decir, $a \times b = b \times a$ ) y es distributivo sobre adición (es decir, $a \times b + c) a \times b + a \times c$ ). El espacio $E$ junto con el producto de la cruz es un álgebra sobre los números reales, que no es ni comunicativo ni asociativo, pero es un álgebra Lie con el producto de la cruz siendo el soporte Lie.

Al igual que el producto punto, depende de la métrica del espacio euclidiano, pero a diferencia del producto punto, también depende de una elección de orientación (o "partididad") del espacio (it' es por eso que se necesita un espacio orientado). En relación con el producto vectorial, el producto exterior de vectores se puede utilizar en dimensiones arbitrarias (con un resultado bivector o de 2 formas) y es independiente de la orientación del espacio.

El producto se puede generalizar de varias maneras, utilizando la orientación y la estructura métrica, al igual que para el producto cruzado tridimensional tradicional, uno puede, en $n$ dimensiones, toma el producto de $n - 1$ vectores para producir un vector perpendicular a todos ellos. Pero si el producto se limita a productos binarios no triviales con resultados vectoriales, existe solo en tres y siete dimensiones. Sin embargo, el producto cruzado en siete dimensiones tiene propiedades indeseables (por ejemplo, no cumple con la identidad de Jacobi), por lo que no se usa en física matemática para representar cantidades como el espacio-tiempo multidimensional. (Ver § Generalizaciones, a continuación, para otras dimensiones).

El producto cruzado con respecto a un sistema de coordenadas derecho

Definición

Encontrar la dirección del producto de la cruz por la regla de la mano derecha

El producto vectorial de dos vectores a y b se define solo en un espacio tridimensional y se denota por a × b. En física y matemáticas aplicadas, la notación de cuña a ∧ b se usa a menudo (junto con el nombre producto vectorial), aunque en matemáticas puras dicha notación suele reservarse solo para el producto exterior, una abstracción del producto vectorial a $n$ dimensiones.

El producto vectorial a × b se define como un vector c que es perpendicular (ortogonal) tanto a a como a b, con una dirección dada por la regla de la mano derecha y una magnitud igual al área del paralelogramo que abarcan los vectores.

El producto vectorial se define mediante la fórmula

{displaystyle mathbf {a} times mathbf {b} =left|mathbf {a} right|left|mathbf {b} right|sin(theta) mathbf {n} }

donde:

Silencio es el ángulo entre a y b en el plano que los contiene (de ahí, es entre 0° y 180°)
.aнельный y нелитеbson las magnitudes de los vectores a y b
y n es un vector unidad perpendicular al plano que contiene a y b, con dirección tal que el conjunto ordenado (a, b, n) es positivamente orientado.

Si los vectores a y b son paralelos (es decir, el ángulo θ entre ellos es 0° o 180°), según la fórmula anterior, el producto vectorial de a y b es el vector cero 0.

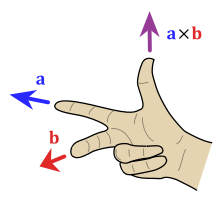
Dirección

El producto cruzado a × b (vertical, en púrpura) cambia como el ángulo entre los vectores a (azul) y b (rojo) cambios. El producto cruzado es siempre ortogonal a ambos vectores, y tiene magnitud cero cuando los vectores son paralelos y máxima magnituda.bCuando son ortogonales.

La dirección del vector n depende de la orientación elegida del espacio. Convencionalmente, viene dado por la regla de la mano derecha, donde uno simplemente apunta el dedo índice de la mano derecha en la dirección de a y el dedo medio en la dirección de b. Entonces, el vector n sale del pulgar (ver la imagen adyacente). El uso de esta regla implica que el producto vectorial es anticonmutativo; es decir, b × a = −(a × b). Al señalar primero con el dedo índice hacia b y luego con el dedo medio hacia a, se forzará al pulgar en la dirección opuesta, invirtiendo el signo del vector producto.

Como el operador del producto vectorial depende de la orientación del espacio, en general, el producto vectorial de dos vectores no es un "verdadero" vector, sino un pseudovector. Consulte § Preferencia de manos para obtener más detalles.

Nombres y origen

Según la regla de Sarrus, el determinante de una matriz 3×3 implica multiplicaciones entre elementos de matriz identificados por diagonales cruzados

En 1842, William Rowan Hamilton descubrió el álgebra de cuaterniones y el producto de Hamilton no conmutativo. En particular, cuando se realiza el producto de Hamilton de dos vectores (es decir, cuaterniones puros con parte escalar cero), se obtiene un cuaternión con parte escalar y vector. La parte escalar y vectorial de este producto de Hamilton corresponde al negativo del producto escalar y el producto vectorial de los dos vectores.

En 1881, Josiah Willard Gibbs y, de forma independiente, Oliver Heaviside, introdujeron la notación tanto para el producto escalar como para el producto vectorial usando un punto (a ⋅ b) y un "×" (a × b), respectivamente, para indicarlos.

En 1877, para enfatizar el hecho de que el resultado de un producto punto es un escalar mientras que el resultado de un producto vectorial es un vector, William Kingdon Clifford acuñó los nombres alternativos producto escalar y producto vectorial de las dos operaciones. Estos nombres alternativos todavía se usan ampliamente en la literatura.

Tanto la notación cruzada (a × b) como el nombre producto cruzado posiblemente se inspiraron en el hecho de que cada componente escalar de a × b se calcula multiplicando los componentes no correspondientes de a y b. Por el contrario, un producto escalar a ⋅ b implica multiplicaciones entre los componentes correspondientes de a y b. Como se explica a continuación, el producto vectorial se puede expresar como un determinante de una matriz especial 3 × 3. Según la regla de Sarrus, esto implica multiplicaciones entre elementos de la matriz identificados por diagonales cruzadas.

Informática

Notación de coordenadas

vectores de base estándar (i, j, k, también denotado e₁, e₂, e₃) y componentes vectoriales de a ()a_x, a_Sí., a_z, también denotado a₁, a₂, a₃)

Si (i, j, k) es una base ortonormal orientada positivamente, los vectores base satisfacen las siguientes igualdades

{displaystyle {begin{alignedat}{2}mathbf {color {blue}{i}} &times mathbf {color {red}{j}} &&=mathbf {color {green}{k}} \mathbf {color {red}{j}} &times mathbf {color {green}{k}} &&=mathbf {color {blue}{i}} \mathbf {color {green}{k}} &times mathbf {color {blue}{i}} &&=mathbf {color {red}{j}} end{alignedat}}}

lo que implica, por la anticonmutatividad del producto vectorial, que

{displaystyle {begin{alignedat}{2}mathbf {color {red}{j}} &times mathbf {color {blue}{i}} &&=-mathbf {color {green}{k}} \mathbf {color {green}{k}} &times mathbf {color {red}{j}} &&=-mathbf {color {blue}{i}} \mathbf {color {blue}{i}} &times mathbf {color {green}{k}} &&=-mathbf {color {red}{j}} end{alignedat}}}

La anticonmutatividad del producto vectorial (y la evidente falta de independencia lineal) también implica que

{displaystyle mathbf {color {blue}{i}} times mathbf {color {blue}{i}} =mathbf {color {red}{j}} times mathbf {color {red}{j}} =mathbf {color {green}{k}} times mathbf {color {green}{k}} =mathbf {0} }

(el vector cero).

Estas igualdades, junto con la distributividad y la linealidad del producto vectorial (aunque ninguna se deduce fácilmente de la definición anterior), son suficientes para determinar el producto vectorial de dos vectores cualesquiera a y b. Cada vector se puede definir como la suma de tres componentes ortogonales paralelas a los vectores base estándar:

{displaystyle {begin{alignedat}{3}mathbf {a} &=a_{1}mathbf {color {blue}{i}} &&+a_{2}mathbf {color {red}{j}} &&+a_{3}mathbf {color {green}{k}} \mathbf {b} &=b_{1}mathbf {color {blue}{i}} &&+b_{2}mathbf {color {red}{j}} &&+b_{3}mathbf {color {green}{k}} end{alignedat}}}

Su producto cruzado a × b se puede expandir usando distributividad:

{displaystyle {begin{aligned}mathbf {a} times mathbf {b} ={}&(a_{1}mathbf {color {blue}{i}} +a_{2}mathbf {color {red}{j}} +a_{3}mathbf {color {green}{k}})times (b_{1}mathbf {color {blue}{i}} +b_{2}mathbf {color {red}{j}} +b_{3}mathbf {color {green}{k}})\={}&a_{1}b_{1}(mathbf {color {blue}{i}} times mathbf {color {blue}{i}})+a_{1}b_{2}(mathbf {color {blue}{i}} times mathbf {color {red}{j}})+a_{1}b_{3}(mathbf {color {blue}{i}} times mathbf {color {green}{k}})+{}\&a_{2}b_{1}(mathbf {color {red}{j}} times mathbf {color {blue}{i}})+a_{2}b_{2}(mathbf {color {red}{j}} times mathbf {color {red}{j}})+a_{2}b_{3}(mathbf {color {red}{j}} times mathbf {color {green}{k}})+{}\&a_{3}b_{1}(mathbf {color {green}{k}} times mathbf {color {blue}{i}})+a_{3}b_{2}(mathbf {color {green}{k}} times mathbf {color {red}{j}})+a_{3}b_{3}(mathbf {color {green}{k}} times mathbf {color {green}{k}})\end{aligned}}}

Esto se puede interpretar como la descomposición de a × b en la suma de nueve productos cruzados más simples que involucran vectores alineado con i, j o k. Cada uno de estos nueve productos cruzados opera sobre dos vectores que son fáciles de manejar ya que son paralelos u ortogonales entre sí. De esta descomposición, usando las igualdades antes mencionadas y reuniendo términos similares, obtenemos:

{displaystyle {begin{aligned}mathbf {a} times mathbf {b} ={}&quad a_{1}b_{1}mathbf {0} +a_{1}b_{2}mathbf {color {green}{k}} -a_{1}b_{3}mathbf {color {red}{j}} \&-a_{2}b_{1}mathbf {color {green}{k}} +a_{2}b_{2}mathbf {0} +a_{2}b_{3}mathbf {color {blue}{i}} \&+a_{3}b_{1}mathbf {color {red}{j}} -a_{3}b_{2}mathbf {color {blue}{i}} +a_{3}b_{3}mathbf {0} \={}&(a_{2}b_{3}-a_{3}b_{2})mathbf {color {blue}{i}} +(a_{3}b_{1}-a_{1}b_{3})mathbf {color {red}{j}} +(a_{1}b_{2}-a_{2}b_{1})mathbf {color {green}{k}} \end{aligned}}}

lo que significa que los tres componentes escalares del vector resultante s = s₁i + s₂j + s₃k = a × b son

{displaystyle {begin{aligned}s_{1}&=a_{2}b_{3}-a_{3}b_{2}\s_{2}&=a_{3}b_{1}-a_{1}b_{3}\s_{3}&=a_{1}b_{2}-a_{2}b_{1}end{aligned}}}

Usando vectores de columna, podemos representar el mismo resultado de la siguiente manera:

{displaystyle {begin{bmatrix}s_{1}\s_{2}\s_{3}end{bmatrix}}={begin{bmatrix}a_{2}b_{3}-a_{3}b_{2}\a_{3}b_{1}-a_{1}b_{3}\a_{1}b_{2}-a_{2}b_{1}end{bmatrix}}}

Notación matricial

Uso de la regla de Sarrus para encontrar el producto de la cruz a y b

El producto vectorial también se puede expresar como el determinante formal:

{displaystyle mathbf {atimes b} ={begin{vmatrix}mathbf {i} &mathbf {j} &mathbf {k} \a_{1}&a_{2}&a_{3}\b_{1}&b_{2}&b_{3}\end{vmatrix}}}

Este determinante se puede calcular usando la regla de Sarrus o la expansión del cofactor. Usando la regla de Sarrus, se expande a

{displaystyle {begin{aligned}mathbf {atimes b} &=(a_{2}b_{3}mathbf {i} +a_{3}b_{1}mathbf {j} +a_{1}b_{2}mathbf {k})-(a_{3}b_{2}mathbf {i} +a_{1}b_{3}mathbf {j} +a_{2}b_{1}mathbf {k})\&=(a_{2}b_{3}-a_{3}b_{2})mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})mathbf {k}.end{aligned}}}

Usando la expansión del cofactor a lo largo de la primera fila, se expande a

{displaystyle {begin{aligned}mathbf {atimes b} &={begin{vmatrix}a_{2}&a_{3}\b_{2}&b_{3}end{vmatrix}}mathbf {i} -{begin{vmatrix}a_{1}&a_{3}\b_{1}&b_{3}end{vmatrix}}mathbf {j} +{begin{vmatrix}a_{1}&a_{2}\b_{1}&b_{2}end{vmatrix}}mathbf {k} \&=(a_{2}b_{3}-a_{3}b_{2})mathbf {i} -(a_{1}b_{3}-a_{3}b_{1})mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})mathbf {k}end{aligned}}}

que da los componentes del vector resultante directamente.

Uso de tensores Levi-Civita

En cualquier base, el producto cruzado $atimes b$ es dado por la fórmula tensorial ${displaystyle E_{ijk}a^{i}b^{j}}$ Donde ${displaystyle E_{ijk}}$ es el inquilino covariante de Levi-Civita (tenemos en cuenta la posición de los índices). Eso corresponde a la fórmula intrínseca dada aquí.
En una base ortonormal teniendo la misma orientación que el espacio, $atimes b$ es dada por la fórmula pseudo-tensorial ${displaystyle varepsilon _{ijk}a^{i}b^{j}}$ Donde ${displaystyle varepsilon _{ijk}}$ es el símbolo Levi-Civita (que es un pseudo-tensor). Esa es la fórmula utilizada para la física cotidiana, pero funciona sólo para esta elección especial de base.
En cualquier base ortonormal, $atimes b$ es dada por la fórmula pseudo-tensorial ${displaystyle (-1)^{B}varepsilon _{ijk}a^{i}b^{j}}$ Donde ${displaystyle (-1)^{B}=pm 1}$ indica si la base tiene la misma orientación que el espacio o no.

La última fórmula evita tener que cambiar la orientación del espacio cuando invertimos una base ortonormal.

Propiedades

Significado geométrico

Gráfico 1. El área de un paralelograma como la magnitud de un producto cruzado

Figura 2. Tres vectores que definen un paralelismo

La magnitud del producto vectorial se puede interpretar como el área positiva del paralelogramo que tiene a y b como lados (ver Figura 1):

{displaystyle left|mathbf {a} times mathbf {b} right|=left|mathbf {a} right|left|mathbf {b} right|left|sin theta right|.}

De hecho, también se puede calcular el volumen V de un paralelepípedo que tiene a, b y c como bordes usando una combinación de un producto cruzado y un producto escalar, llamado producto triple escalar (ver Figura 2):

{displaystyle mathbf {a} cdot (mathbf {b} times mathbf {c})=mathbf {b} cdot (mathbf {c} times mathbf {a})=mathbf {c} cdot (mathbf {a} times mathbf {b}).}

Como el resultado del triple producto escalar puede ser negativo, el volumen del paralelepípedo viene dado por su valor absoluto:

V=|mathbf {a} cdot (mathbf {b} times mathbf {c})|.

Debido a que la magnitud del producto vectorial depende del seno del ángulo entre sus argumentos, el producto vectorial puede considerarse como una medida de perpendicularidad de la misma manera que el producto vectorial es un medida de paralelismo. Dados dos vectores unitarios, su producto vectorial tiene una magnitud de 1 si los dos son perpendiculares y una magnitud de cero si los dos son paralelos. El producto punto de dos vectores unitarios se comporta de manera opuesta: es cero cuando los vectores unitarios son perpendiculares y 1 si los vectores unitarios son paralelos.

Los vectores unitarios permiten dos identidades convenientes: el producto escalar de dos vectores unitarios produce el coseno (que puede ser positivo o negativo) del ángulo entre los dos vectores unitarios. La magnitud del producto vectorial de los dos vectores unitarios produce el seno (que siempre será positivo).

Propiedades algebraicas

Multiplicación de escalar de productos cruzados. Izquierda: Decomposición de b en componentes paralelos y perpendiculares a a. Bien. Escalado de los componentes perpendiculares por un número real positivo r (si es negativo, b y el producto cruzado se invierte).

Distribución de productos cruzados sobre la adición de vectores. Izquierda: Los vectores b y c se resuelven en componentes paralelos y perpendiculares a a. Bien. Los componentes paralelos desaparecen en el producto cruzado, sólo los componentes perpendiculares mostrados en el plano perpendicular a a permanecer.

Los dos productos de tres vectores sin igual a, b, c. En cada caso, dos vectores definen un plano, el otro está fuera del plano y puede dividirse en componentes paralelos y perpendiculares al producto transversal de los vectores que definen el plano. Estos componentes pueden ser encontrados por proyección y rechazo vectorial. El triple producto está en el plano y se gira como se muestra.

Si el producto vectorial de dos vectores es el vector cero (es decir, a × b = 0), entonces una o ambas entradas es el vector cero, (a = 0 o b = 0) o bien son paralelos o antiparalelos (a ∥ b) de modo que el seno del ángulo entre ellos sea cero (θ = 0 ° o θ = 180° y sin θ = 0).

El autoproducto vectorial de un vector es el vector cero:

{displaystyle mathbf {a} times mathbf {a} =mathbf {0}.}

El producto vectorial es anticonmutativo,

mathbf {a} times mathbf {b} =-(mathbf {b} times mathbf {a}),

distributivo sobre suma,

mathbf {a} times (mathbf {b} +mathbf {c})=(mathbf {a} times mathbf {b})+(mathbf {a} times mathbf {c}),

y compatible con la multiplicación escalar de modo que

{displaystyle (r,mathbf {a})times mathbf {b} =mathbf {a} times (r,mathbf {b})=r,(mathbf {a} times mathbf {b}).}

No es asociativo, pero satisface la identidad de Jacobi:

mathbf {a} times (mathbf {b} times mathbf {c})+mathbf {b} times (mathbf {c} times mathbf {a})+mathbf {c} times (mathbf {a} times mathbf {b})=mathbf {0}.

La distributividad, la linealidad y la identidad de Jacobi muestran que el espacio vectorial R³ junto con la suma vectorial y el producto vectorial forman un álgebra de Lie, el álgebra de Lie de la ortogonal real grupo en 3 dimensiones, SO(3). El producto cruz no obedece la ley de cancelación; es decir, a × b = a × c con a ≠ 0 no implica b = c, pero solo eso:

{displaystyle {begin{aligned}mathbf {0} &=(mathbf {a} times mathbf {b})-(mathbf {a} times mathbf {c})\&=mathbf {a} times (mathbf {b} -mathbf {c}).\end{aligned}}}

Este puede ser el caso donde b y c cancelan, pero además donde a y b − c son paralelos; es decir, están relacionados por un factor de escala t, lo que lleva a:

{displaystyle mathbf {c} =mathbf {b} +t,mathbf {a}}

para algún escalar t.

Si, además de a × b = a × c y a ≠ 0 como arriba, se da el caso de que a ⋅ b = a ⋅ c entonces

{displaystyle {begin{aligned}mathbf {a} times (mathbf {b} -mathbf {c})&=mathbf {0} \mathbf {a} cdot (mathbf {b} -mathbf {c})&=0,end{aligned}}}

Como b − c no pueden ser simultáneamente paralelos (para que el producto vectorial sea 0) y perpendicular (para que el producto escalar sea 0) a a, debe darse el caso de que b y c se cancelen: b = c.

De la definición geométrica, el producto vectorial es invariable bajo rotaciones apropiadas sobre el eje definido por a × b. En fórmulas:

(Rmathbf {a})times (Rmathbf {b})=R(mathbf {a} times mathbf {b})

, donde

R

es una matriz de rotación con

det(R)=1

Más generalmente, el producto vectorial obedece a la siguiente identidad bajo transformaciones de matrices:

{displaystyle (Mmathbf {a})times (Mmathbf {b})=(det M)left(M^{-1}right)^{mathrm {T} }(mathbf {a} times mathbf {b})=operatorname {cof} M(mathbf {a} times mathbf {b})}

Donde $M$ es una matriz de 3 por 3 ${displaystyle left(M^{-1}right)^{mathrm {T} }}$ es la transposición del inverso y ${displaystyle operatorname {cof} }$ es la matriz del cofactor. Se puede ver fácilmente cómo esta fórmula se reduce a la anterior si $M$ es una matriz de rotación. Si $M$ es una matriz simétrica de 3 por 3 aplicada a un producto cruzado genérico $mathbf{a} times mathbf{b}$ , la siguiente relación es verdadera:

{displaystyle M(mathbf {a} times mathbf {b})=operatorname {Tr} (M)(mathbf {a} times mathbf {b})-mathbf {a} times Mmathbf {b} +mathbf {b} times Mmathbf {a} }

El producto vectorial de dos vectores se encuentra en el espacio nulo de la matriz 2 × 3 con los vectores como filas:

mathbf {a} times mathbf {b} in NSleft({begin{bmatrix}mathbf {a} \mathbf {b} end{bmatrix}}right).

Para la suma de dos productos cruzados, se cumple la siguiente identidad:

mathbf {a} times mathbf {b} +mathbf {c} times mathbf {d} =(mathbf {a} -mathbf {c})times (mathbf {b} -mathbf {d})+mathbf {a} times mathbf {d} +mathbf {c} times mathbf {b}.

Diferenciación

La regla del producto del cálculo diferencial se aplica a cualquier operación bilineal y, por lo tanto, también al producto vectorial:

{displaystyle {frac {d}{dt}}(mathbf {a} times mathbf {b})={frac {dmathbf {a} }{dt}}times mathbf {b} +mathbf {a} times {frac {dmathbf {b} }{dt}},}

donde a y b son vectores que dependen de la variable real t.

Expansión de triple producto

El producto vectorial se usa en ambas formas del producto triple. El triple producto escalar de tres vectores se define como

mathbf {a} cdot (mathbf {b} times mathbf {c}),

Es el volumen con signo del paralelepípedo con aristas a, b y c y como tal los vectores se pueden usar en cualquier orden eso es una permutación uniforme del orden anterior. Por lo tanto, los siguientes son iguales:

mathbf {a} cdot (mathbf {b} times mathbf {c})=mathbf {b} cdot (mathbf {c} times mathbf {a})=mathbf {c} cdot (mathbf {a} times mathbf {b}),

El producto vectorial triple es el producto vectorial de un vector con el resultado de otro producto vectorial, y está relacionado con el producto escalar mediante la siguiente fórmula

{displaystyle {begin{aligned}mathbf {a} times (mathbf {b} times mathbf {c})=mathbf {b} (mathbf {c} cdot mathbf {a})-mathbf {c} (mathbf {a} cdot mathbf {b})\(mathbf {a} times mathbf {b})times mathbf {c} =mathbf {b} (mathbf {c} cdot mathbf {a})-mathbf {a} (mathbf {b} cdot mathbf {c})end{aligned}}}

El mnemotécnico "BAC menos CAB" se utiliza para recordar el orden de los vectores en el miembro de la derecha. Esta fórmula se usa en física para simplificar los cálculos vectoriales. Un caso especial, relacionado con gradientes y útil en cálculo vectorial, es

{displaystyle {begin{aligned}nabla times (nabla times mathbf {f})&=nabla (nabla cdot mathbf {f})-(nabla cdot nabla)mathbf {f} \&=nabla (nabla cdot mathbf {f})-nabla ^{2}mathbf {f}\end{aligned}}}

donde ∇² es el operador vectorial laplaciano.

Otras identidades relacionan el producto vectorial con el producto triple escalar:

{displaystyle {begin{aligned}(mathbf {a} times mathbf {b})times (mathbf {a} times mathbf {c})&=(mathbf {a} cdot (mathbf {b} times mathbf {c}))mathbf {a} \(mathbf {a} times mathbf {b})cdot (mathbf {c} times mathbf {d})&=mathbf {b} ^{mathrm {T} }left(left(mathbf {c} ^{mathrm {T} }mathbf {a} right)I-mathbf {c} mathbf {a} ^{mathrm {T} }right)mathbf {d} \&=(mathbf {a} cdot mathbf {c})(mathbf {b} cdot mathbf {d})-(mathbf {a} cdot mathbf {d})(mathbf {b} cdot mathbf {c})end{aligned}}}

donde I es la matriz identidad.

Formulación alternativa

El producto cruz y el producto escalar están relacionados por:

{displaystyle left|mathbf {a} times mathbf {b} right|^{2}=left|mathbf {a} right|^{2}left|mathbf {b} right|^{2}-(mathbf {a} cdot mathbf {b})^{2}.}

El lado derecho es el Gram determinante de a y b, el cuadrado del área del paralelogramo definido por los vectores. Esta condición determina la magnitud del producto vectorial. Es decir, dado que el producto escalar se define, en términos del ángulo θ entre los dos vectores, como:

mathbf {acdot b} =left|mathbf {a} right|left|mathbf {b} right|cos theta

La relación anterior se puede reescribir de la siguiente manera:

left|mathbf {atimes b} right|^{2}=left|mathbf {a} right|^{2}left|mathbf {b} right|^{2}left(1-cos ^{2}theta right).

Invocando la identidad trigonométrica de Pitágoras se obtiene:

left|mathbf {a} times mathbf {b} right|=left|mathbf {a} right|left|mathbf {b} right|left|sin theta right|,

que es la magnitud del producto vectorial expresada en términos de θ, igual al área del paralelogramo definido por a y b (ver definición arriba).

La combinación de este requisito y la propiedad de que el producto vectorial sea ortogonal a sus constituyentes a y b proporciona una definición alternativa del producto vectorial.

La identidad de Lagrange

La relación:

{displaystyle left|mathbf {a} times mathbf {b} right|^{2}equiv det {begin{bmatrix}mathbf {a} cdot mathbf {a} &mathbf {a} cdot mathbf {b} \mathbf {a} cdot mathbf {b} &mathbf {b} cdot mathbf {b} \end{bmatrix}}equiv left|mathbf {a} right|^{2}left|mathbf {b} right|^{2}-(mathbf {a} cdot mathbf {b})^{2}.}

se puede comparar con otra relación que implica el lado derecho, a saber, la identidad de Lagrange expresada como:

<math alttext="{displaystyle sum _{1leq i.. 1≤ ≤ i.j≤ ≤ n()aibj− − ajbi)2↑ ↑ .a.2.b.2− − ()a⋅ ⋅ b)2,{displaystyle sum _{1leq iSeguido (a_{i}b_{j}-a_{j}b_{i}right)^{2}equiv left eternamathbf {a}rightf}leftmathbf {b}derechaf}-(mathbf {acdot b})}<img alt="{displaystyle sum _{1leq i

donde a y b pueden ser vectores de n dimensiones. Esto también muestra que la forma de volumen de Riemann para superficies es exactamente el elemento de superficie del cálculo vectorial. En el caso de que n = 3, la combinación de estas dos ecuaciones da como resultado la expresión de la magnitud del producto vectorial en términos de sus componentes:

<math alttext="{displaystyle {begin{aligned}&left|mathbf {a} times mathbf {b} right|^{2}equiv sum _{1leq i.a× × b.2↑ ↑ .. 1≤ ≤ i.j≤ ≤ 3()aibj− − ajbi)2↑ ↑ ()a1b2− − b1a2)2+()a2b3− − a3b2)2+()a3b1− − a1b3)2.{displaystyle {begin{aligned} {leftfnMitbf {a} times mathbf {b} righth00}equiv sum _{1leq i didjleq 3}left (a_{i}b_{j}-a_{j}b_{i}right)^{2}\equiv {2}a_{2}a_{2}a_{2}right)^{2}+left(a_{2}b_{3}-a_{3}b_{2}right)^{2}+left(a_{3}b_{1}-a_{1}b_{3}right)}{2}right)}{2}}}}}}{2}}}}}}}}{2}}}}}}}}}}{2}}}}}}}}}}}}}}}}}}}}}}}}}}left}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}<img alt="{displaystyle {begin{aligned}&left|mathbf {a} times mathbf {b} right|^{2}equiv sum _{1leq i

El mismo resultado se encuentra directamente usando los componentes del producto cruzado encontrado a partir de:

{displaystyle mathbf {a} times mathbf {b} equiv det {begin{bmatrix}{hat {mathbf {i} }}&{hat {mathbf {j} }}&{hat {mathbf {k} }}\a_{1}&a_{2}&a_{3}\b_{1}&b_{2}&b_{3}\end{bmatrix}}.}

En R³, la ecuación de Lagrange es un caso especial de la multiplicatividad |vw| = |v||w| de la norma en el álgebra de cuaterniones.

Es un caso especial de otra fórmula, a veces también llamada identidad de Lagrange, que es el caso tridimensional de la identidad de Binet-Cauchy:

{displaystyle (mathbf {a} times mathbf {b})cdot (mathbf {c} times mathbf {d})equiv (mathbf {a} cdot mathbf {c})(mathbf {b} cdot mathbf {d})-(mathbf {a} cdot mathbf {d})(mathbf {b} cdot mathbf {c}).}

Si a = c y b = d esto se simplifica a la fórmula anterior.

Generadores infinitesimales de rotaciones

El producto vectorial describe convenientemente los generadores infinitesimales de rotaciones en R³. Específicamente, si n es un vector unitario en R³ y R(φ, n) denota una rotación alrededor del eje a través del origen especificado por n, con ángulo φ (medido en radianes, en sentido antihorario cuando se ve desde la punta de n), entonces

left.{d over dphi }right|_{phi =0}R(phi{boldsymbol {n}}){boldsymbol {x}}={boldsymbol {n}}times {boldsymbol {x}}

para cada vector x en R³. El producto vectorial con n por lo tanto describe el generador infinitesimal de las rotaciones alrededor de n. Estos generadores infinitesimales forman el álgebra de Lie so(3) del grupo de rotación SO(3), y obtenemos el resultado de que el álgebra de Lie R³ con producto vectorial es isomorfo al álgebra de Lie so(3).

Formas alternativas de calcular

Conversión a multiplicación de matrices

El producto vectorial vectorial también se puede expresar como el producto de una matriz asimétrica y un vector:

{displaystyle {begin{aligned}mathbf {a} times mathbf {b} =[mathbf {a} ]_{times }mathbf {b} &={begin{bmatrix},0&!-a_{3}&,,a_{2}\,,a_{3}&0&!-a_{1}\-a_{2}&,,a_{1}&,0end{bmatrix}}{begin{bmatrix}b_{1}\b_{2}\b_{3}end{bmatrix}}\mathbf {a} times mathbf {b} ={[mathbf {b} ]_{times }}^{mathrm {!!T} }mathbf {a} &={begin{bmatrix},0&,,b_{3}&!-b_{2}\-b_{3}&0&,,b_{1}\,,b_{2}&!-b_{1}&,0end{bmatrix}}{begin{bmatrix}a_{1}\a_{2}\a_{3}end{bmatrix}},end{aligned}}}

T

a_×

{displaystyle [mathbf {a} ]_{times }{stackrel {rm {def}}{=}}{begin{bmatrix},,0&!-a_{3}&,,,a_{2}\,,,a_{3}&0&!-a_{1}\!-a_{2}&,,a_{1}&,,0end{bmatrix}}.}

Las columnas [a]_×,i de la matriz simétrica oblicua para un vector a también se pueden obtener calculando la cruz producto con vectores unitarios. Eso es,

{displaystyle [mathbf {a} ]_{timesi}=mathbf {a} times mathbf {{hat {e}}_{i}};iin {1,2,3}}

{displaystyle [mathbf {a} ]_{times }=sum _{i=1}^{3}left(mathbf {a} times mathbf {{hat {e}}_{i}} right)otimes mathbf {{hat {e}}_{i}}}

otimes

Además, si a se expresa como un producto cruzado:

{displaystyle mathbf {a} =mathbf {c} times mathbf {d} }

{displaystyle [mathbf {a} ]_{times }=mathbf {d} mathbf {c} ^{mathrm {T} }-mathbf {c} mathbf {d} ^{mathrm {T} }.}

Prueba por sustitución

Evaluación del producto cruzado

{displaystyle mathbf {a} =mathbf {c} times mathbf {d} ={begin{pmatrix}c_{2}d_{3}-c_{3}d_{2}\c_{3}d_{1}-c_{1}d_{3}\c_{1}d_{2}-c_{2}d_{1}end{pmatrix}}}

Por lo tanto, el lado izquierdo es igual

{displaystyle [mathbf {a} ]_{times }={begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0end{bmatrix}}}

Ahora, por el lado derecho,

{displaystyle mathbf {c} mathbf {d} ^{mathrm {T} }={begin{bmatrix}c_{1}d_{1}&c_{1}d_{2}&c_{1}d_{3}\c_{2}d_{1}&c_{2}d_{2}&c_{2}d_{3}\c_{3}d_{1}&c_{3}d_{2}&c_{3}d_{3}end{bmatrix}}}

Y su transpose es

{displaystyle mathbf {d} mathbf {c} ^{mathrm {T} }={begin{bmatrix}c_{1}d_{1}&c_{2}d_{1}&c_{3}d_{1}\c_{1}d_{2}&c_{2}d_{2}&c_{3}d_{2}\c_{1}d_{3}&c_{2}d_{3}&c_{3}d_{3}end{bmatrix}}}

Evaluación del lado derecho

{displaystyle mathbf {d} mathbf {c} ^{mathrm {T} }-mathbf {c} mathbf {d} ^{mathrm {T} }={begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0end{bmatrix}}}

La comparación muestra que el lado izquierdo iguala el lado derecho.

Este resultado se puede generalizar a dimensiones más altas usando álgebra geométrica. En particular, en cualquier dimensión, los bivectores se pueden identificar con matrices simétricas oblicuas, por lo que el producto entre una matriz simétrica y un vector es equivalente a la parte de grado 1 del producto de un bivector y un vector. En tres dimensiones, los bivectores son duales a los vectores, por lo que el producto es equivalente al producto cruzado, con el bivector en lugar de su vector dual. En dimensiones más altas, el producto aún se puede calcular, pero los bivectores tienen más grados de libertad y no son equivalentes a los vectores.

Esta notación también suele ser mucho más fácil de trabajar, por ejemplo, en geometría epipolar.

De las propiedades generales del producto vectorial se sigue inmediatamente que

{displaystyle [mathbf {a} ]_{times },mathbf {a} =mathbf {0} }

{displaystyle mathbf {a} ^{mathrm {T} },[mathbf {a} ]_{times }=mathbf {0} }

a_×

{displaystyle mathbf {b} ^{mathrm {T} },[mathbf {a} ]_{times },mathbf {b} =0.}

La expansión del producto triple mencionada anteriormente (regla bac-cab) se puede demostrar fácilmente usando esta notación.

Como se mencionó anteriormente, el álgebra de Lie R³ con producto vectorial es isomorfa al álgebra de Lie so(3), cuyos elementos pueden identificarse con las matrices simétricas oblicuas de 3 × 3. El mapa a → [a]_× proporciona un isomorfismo entre R³ y entonces(3). Bajo este mapa, el producto cruzado de 3 vectores corresponde al conmutador de matrices simétricas oblicuas de 3x3.

Conversión de matriz para producto cruzado con vectores base canónica

Denotar con

{displaystyle mathbf {e} _{i}in mathbf {R} ^{3times 1}}

i

-el vector base canónico, el producto cruzado de un vector genérico

{displaystyle mathbf {v} in mathbf {R} ^{3times 1}}

con

mathbf {e} _{i}

es dado por:

mathbf{v} times mathbf{e}_i = mathbf{C}_i mathbf{v}

, donde

{displaystyle mathbf {C} _{1}={begin{bmatrix}0&0&0\0&0&1\0&-1&0end{bmatrix}},quad mathbf {C} _{2}={begin{bmatrix}0&0&-1\0&0&0\1&0&0end{bmatrix}},quad mathbf {C} _{3}={begin{bmatrix}0&1&0\-1&0&0\0&0&0end{bmatrix}}}

Estas matrices comparten las siguientes propiedades:

${displaystyle mathbf {C} _{i}^{textrm {T}}=-mathbf {C} _{i}}$ (skew-symmetric);
Ambos rastros y determinantes son cero;
${displaystyle {text{rank}}(mathbf {C} _{i})=2}$ ;
${displaystyle mathbf {C} _{i}mathbf {C} _{i}^{textrm {T}}=mathbf {P} _{mathbf {e} _{i}}^{^{perp }}}$ (véase infra);

La matriz de proyección ortogonal de un vector $mathbf{v} neq mathbf{0}$ es dado por ${displaystyle mathbf {P} _{mathbf {v} }=mathbf {v} left(mathbf {v} ^{textrm {T}}mathbf {v} right)^{-1}mathbf {v} ^{T}}$ . La matriz de proyección sobre el complemento ortogonal es dada por $mathbf{P}^{ ^perp}_{mathbf{v}} = mathbf{I} - mathbf{P}_{mathbf{v}}$ , donde $mathbf {I}$ es la matriz de identidad. Para el caso especial $mathbf{v} = mathbf{e}_i$ , se puede verificar que

{displaystyle mathbf {P} _{mathbf {e} _{1}}^{^{perp }}={begin{bmatrix}0&0&0\0&1&0\0&0&1end{bmatrix}},quad mathbf {P} _{mathbf {e} _{2}}^{^{perp }}={begin{bmatrix}1&0&0\0&0&0\0&0&1end{bmatrix}},quad mathbf {P} _{mathbf {e} _{3}}^{^{perp }}={begin{bmatrix}1&0&0\0&1&0\0&0&0end{bmatrix}}}

Para otras propiedades de matrices de proyección ortogonal, vea proyección (álgebra lineal).

Notación de índice para tensores

El producto vectorial se puede definir alternativamente en términos del tensor de Levi-Civita E_ijk y un producto escalar η^mi , que son útiles para convertir notación vectorial para aplicaciones de tensor:

{displaystyle mathbf {c} =mathbf {atimes b} Leftrightarrow c^{m}=sum _{i=1}^{3}sum _{j=1}^{3}sum _{k=1}^{3}eta ^{mi}E_{ijk}a^{j}b^{k}}

donde los índices $i,j,k$ corresponden a componentes vectoriales. Esta caracterización del producto cruzado se expresa a menudo más compactamente utilizando la convención de summación de Einstein como

{displaystyle mathbf {c} =mathbf {atimes b} Leftrightarrow c^{m}=eta ^{mi}E_{ijk}a^{j}b^{k}}

en el que se suman índices repetidos sobre los valores 1 a 3.

En una base ortonormal positiva .^# = δ^# (el Kronecker delta) y ${displaystyle E_{ijk}=varepsilon _{ijk}}$ (el símbolo Levi-Civita). En ese caso, esta representación es otra forma de la representación simétrica del producto cruzado:

{displaystyle [varepsilon _{ijk}a^{j}]=[mathbf {a} ]_{times }.}

En mecánica clásica: la representación del producto vectorial mediante el uso del símbolo de Levi-Civita puede hacer que las simetrías mecánicas sean obvias cuando los sistemas físicos son isotrópicos. (Un ejemplo: considere una partícula en un potencial de la Ley de Hooke en tres espacios, libre de oscilar en tres dimensiones; ninguna de estas dimensiones es "especial" en ningún sentido, por lo que las simetrías se encuentran en el momento angular representado por el producto cruzado, que se aclaran mediante la representación de Levi-Civita mencionada anteriormente).

Mnemónico

Mnemonic para calcular un producto cruzado en forma vectorial

La palabra "xyzzy" se puede utilizar para recordar la definición del producto cruz.

mathbf {a} =mathbf {b} times mathbf {c}

donde:

{displaystyle mathbf {a} ={begin{bmatrix}a_{x}\a_{y}\a_{z}end{bmatrix}}, mathbf {b} ={begin{bmatrix}b_{x}\b_{y}\b_{z}end{bmatrix}}, mathbf {c} ={begin{bmatrix}c_{x}\c_{y}\c_{z}end{bmatrix}}}

entonces:

{displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}}

{displaystyle a_{y}=b_{z}c_{x}-b_{x}c_{z}}

{displaystyle a_{z}=b_{x}c_{y}-b_{y}c_{x}.}

La segunda y tercera ecuaciones se pueden obtener de la primera simplemente girando verticalmente los subíndices, x → y → z → x. El problema, por supuesto, es cómo recordar la primera ecuación, y hay dos opciones disponibles para este propósito: recordar las dos diagonales relevantes del esquema de Sarrus (aquellas que contienen i), o para recordar la secuencia xyzzy.

Dado que la primera diagonal en el esquema de Sarrus es solo la diagonal principal de la matriz 3×3 mencionada anteriormente, las primeras tres letras de la palabra xyzzy se pueden recordar muy fácilmente.

Visualización cruzada

De manera similar al recurso mnemotécnico anterior, una "cruz" o X se puede visualizar entre los dos vectores en la ecuación. Esto puede ser útil para recordar la fórmula correcta del producto cruzado.

mathbf {a} =mathbf {b} times mathbf {c}

entonces:

{displaystyle mathbf {a} ={begin{bmatrix}b_{x}\b_{y}\b_{z}end{bmatrix}}times {begin{bmatrix}c_{x}\c_{y}\c_{z}end{bmatrix}}.}

Si queremos obtener la fórmula para $a_{x}$ simplemente dejamos caer $b_{x}$ y $c_{x}$ de la fórmula, y tomar los siguientes dos componentes abajo:

{displaystyle a_{x}={begin{bmatrix}b_{y}\b_{z}end{bmatrix}}times {begin{bmatrix}c_{y}\c_{z}end{bmatrix}}.}

Cuando haces esto por $a_{y}$ los siguientes dos elementos abajo deben "envolver alrededor" la matriz para que después del componente z venga el componente x. Para claridad, al realizar esta operación para $a_{y}$ , los dos componentes siguientes deben ser z y x (en ese orden). Mientras que $a_{z}$ los dos componentes siguientes deben ser tomados como x y y.

{displaystyle a_{y}={begin{bmatrix}b_{z}\b_{x}end{bmatrix}}times {begin{bmatrix}c_{z}\c_{x}end{bmatrix}}, a_{z}={begin{bmatrix}b_{x}\b_{y}end{bmatrix}}times {begin{bmatrix}c_{x}\c_{y}end{bmatrix}}}

Para $a_{x}$ entonces, si visualizamos al operador cruzado como apuntando desde un elemento a la izquierda a un elemento a la derecha, podemos tomar el primer elemento a la izquierda y simplemente multiplicar por el elemento que la cruz apunta a la matriz de la derecha. Luego restamos el siguiente elemento a la izquierda, multiplicado por el elemento que la cruz apunta aquí también. Esto resulta en nuestro $a_{x}$ fórmula –

{displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}.}

Podemos hacerlo de la misma manera $a_{y}$ y $a_{z}$ para construir sus fórmulas asociadas.

Aplicaciones

El producto cruz tiene aplicaciones en varios contextos. Por ejemplo, se utiliza en geometría computacional, física e ingeniería. A continuación se incluye una lista no exhaustiva de ejemplos.

Geometría computacional

El producto vectorial aparece en el cálculo de la distancia de dos líneas oblicuas (líneas que no están en el mismo plano) entre sí en un espacio tridimensional.

El producto vectorial se puede utilizar para calcular la normal de un triángulo o polígono, una operación que se realiza con frecuencia en los gráficos por computadora. Por ejemplo, el giro de un polígono (hacia la derecha o hacia la izquierda) alrededor de un punto dentro del polígono se puede calcular triangulando el polígono (como si se tratara de una rueda) y sumando los ángulos (entre los radios) usando el producto cruzado para realizar un seguimiento de la signo de cada ángulo.

En geometría computacional del plano, el producto transversal se utiliza para determinar el signo del ángulo agudo definido por tres puntos ${displaystyle p_{1}=(x_{1},y_{1}),p_{2}=(x_{2},y_{2})}$ y ${displaystyle p_{3}=(x_{3},y_{3})}$ . Corresponde a la dirección (hasta arriba o hacia abajo) del producto cruzado de los dos vectores coplanar definidos por los dos pares de puntos ${displaystyle (p_{1},p_{2})}$ y ${displaystyle (p_{1},p_{3})}$ . El signo del ángulo agudo es el signo de la expresión

{displaystyle P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1}),}

que es la longitud con signo del producto vectorial de los dos vectores.

En el sistema de coordenadas "derecha", si el resultado es 0, los puntos son collinear; si es positivo, los tres puntos constituyen un ángulo positivo de rotación alrededor $p_{1}$ desde ${displaystyle p_{2}}$ a ${displaystyle p_{3}}$ , de lo contrario un ángulo negativo. Desde otro punto de vista, el signo de $P$ dice si ${displaystyle p_{3}}$ mentiras a la izquierda o a la derecha de la línea ${displaystyle p_{1},p_{2}.}$

El producto vectorial se utiliza para calcular el volumen de un poliedro, como un tetraedro o un paralelepípedo.

Momento angular y par

El momento angular $L$ de una partícula sobre un origen dado se define como:

{displaystyle mathbf {L} =mathbf {r} times mathbf {p}}

donde $r$ es el vector de posición de la partícula relativo al origen, $p$ es el momento lineal de la partícula.

Del mismo modo, el momento $M$ de una fuerza $F B$ aplicado en el punto B alrededor del punto A se da como:

mathbf {M} _{mathrm {A} }=mathbf {r} _{mathrm {AB} }times mathbf {F} _{mathrm {B} },

En mecánica el momento de la fuerza también se llama torque y escrito como ${displaystyle mathbf {tau } }$

Desde la posición $r$ , impulso lineal $p$ y fuerza $F$ son todos vectores verdaderos, tanto el momento angular $L$ y el momento de una fuerza $M$ son pseudovectores o vectores axiales.

Cuerpo rígido

El producto cruz aparece con frecuencia en la descripción de movimientos rígidos. Dos puntos P y Q en un cuerpo rígido se pueden relacionar mediante:

{displaystyle mathbf {v} _{P}-mathbf {v} _{Q}={boldsymbol {omega }}times left(mathbf {r} _{P}-mathbf {r} _{Q}right),}

Donde $mathbf {r}$ es la posición del punto, $mathbf {v}$ es su velocidad y ${boldsymbol omega }$ es la velocidad angular del cuerpo.

Desde la posición $mathbf {r}$ y velocidad $mathbf {v}$ son verdadero vectores, la velocidad angular ${boldsymbol omega }$ es un pseudovector o vector axial.

Fuerza de Lorentz

El producto vectorial se usa para describir la fuerza de Lorentz experimentada por una carga eléctrica en movimiento $q e$ :

{displaystyle mathbf {F} =q_{e}left(mathbf {E} +mathbf {v} times mathbf {B} right)}

Dado que la velocidad $v$ , fuerza $F$ y el campo eléctrico $E$ son todos vectores verdaderos, el campo magnético $B$ es un pseudovector.

Otro

En cálculo vectorial, el producto vectorial se utiliza para definir la fórmula del operador vectorial rotacional.

El truco de reescribir un producto cruzado en términos de una multiplicación de matrices aparece con frecuencia en la geometría epipolar y de vista múltiple, en particular cuando se derivan restricciones coincidentes.

Como producto externo

El producto cruzado en relación con el producto exterior. En rojo están el vector de unidad ortogonal, y el bivector de unidad "parallel".

El producto cruz se puede definir en términos del producto exterior. Se puede generalizar a un producto externo en otras dimensiones que no sean tres. Esta vista permite una interpretación geométrica natural del producto cruz. En álgebra exterior el producto exterior de dos vectores es un bivector. Un bivector es un elemento plano orientado, de la misma manera que un vector es un elemento lineal orientado. Dados dos vectores a y b, uno puede ver el bivector a ∧ b como el paralelogramo orientado dividido por a y b. Luego, el producto vectorial se obtiene tomando la estrella de Hodge del bivector a ∧ b, asignando 2 vectores a vectores:

{displaystyle atimes b=star (awedge b).}

Esto se puede considerar como el elemento multidimensional orientado "perpendicular" al bivector. Solo en tres dimensiones el resultado es un elemento unidimensional orientado, un vector, mientras que, por ejemplo, en cuatro dimensiones, el dual de Hodge de un bivector es bidimensional, un bivector. Por lo tanto, solo en tres dimensiones se puede definir un vector producto cruzado de a y b como el vector dual del bivector a ∧ b: es perpendicular al bivector, con orientación que depende de la lateralidad del sistema de coordenadas, y tiene la misma magnitud relativa al vector unitario normal que a ∧ b tiene relativo al bivector unitario; precisamente las propiedades descritas anteriormente.

Manualidad

Coherencia

Cuando las leyes de la física se escriben como ecuaciones, es posible elegir arbitrariamente el sistema de coordenadas, incluida la lateralidad. Se debe tener cuidado de nunca escribir una ecuación en la que los dos lados no se comporten de la misma manera en todas las transformaciones que deben considerarse. Por ejemplo, si un lado de la ecuación es un producto cruzado de dos vectores polares, se debe tener en cuenta que el resultado es un vector axial. Por lo tanto, por coherencia, el otro lado también debe ser un vector axial. Más generalmente, el resultado de un producto vectorial puede ser un vector polar o un vector axial, según el tipo de sus operandos (vectores polares o vectores axiales). Es decir, los vectores polares y los vectores axiales están interrelacionados de las siguientes maneras bajo la aplicación del producto vectorial:

vector polar × vector polar = vector axial
vector axial × vector axial = vector axial
vector polar × vector axial = vector polar
vector axial × vector polar = vector polar

o simbólicamente

polar × polar = axial
axial × axial = axial
polar × axial = polar
axial × polar = polar

Debido a que el producto vectorial también puede ser un vector polar, es posible que no cambie de dirección con una transformación de imagen especular. Esto sucede, según las relaciones anteriores, si uno de los operandos es un vector polar y el otro es un vector axial (por ejemplo, el producto vectorial de dos vectores polares). Por ejemplo, un vector triple producto que implica tres vectores polares es un vector polar.

Es posible un enfoque sin manos usando álgebra exterior.

La paradoja de la base ortonormal

Sea (i, j,k) una base ortonormal. Los vectores i, j y k no dependen de la orientación del espacio. Incluso se pueden definir en ausencia de cualquier orientación. Por tanto, no pueden ser vectores axiales. Pero si i y j son vectores polares entonces k es un vector axial para i × j = k o j × i = k. Esto es una paradoja.

"Axial" y "polar" son calificadores físicos para vectores físicos; es decir, vectores que representan cantidades físicas como la velocidad o el campo magnético. Los vectores i, j y k son vectores matemáticos, ni axiales ni polares. En matemáticas, el producto cruzado de dos vectores es un vector. No hay contradicción.

Generalizaciones

Hay varias formas de generalizar el producto vectorial a dimensiones superiores.

Álgebra de mentira

El producto vectorial puede verse como uno de los productos de Lie más simples y, por lo tanto, se generaliza mediante álgebras de Lie, que se axiomatizan como productos binarios que satisfacen los axiomas de multilinealidad, asimetría sesgada y la identidad de Jacobi. Existen muchas álgebras de Lie, y su estudio es un campo importante de las matemáticas, llamado teoría de Lie.

Por ejemplo, el álgebra Heisenberg da otra estructura de álgebra de Lie en ${displaystyle mathbf {R} ^{3}.}$ Sobre la base ${displaystyle {x,y,z},}$ el producto es ${displaystyle [x,y]=z,[x,z]=[y,z]=0.}$

Cuaterniones

El producto vectorial también se puede describir en términos de cuaterniones. En general, si un vector [a₁, a₂, a₃] se representa como el cuaternión a₁i + a₂j + a₃k, el producto vectorial de dos vectores se puede obtener tomando su producto como cuaterniones y eliminando la parte real del resultado. La parte real será el negativo del producto escalar de los dos vectores.

Octoniones

Se puede obtener un producto cruzado para vectores de 7 dimensiones de la misma manera usando los octoniones en lugar de los cuaterniones. La inexistencia de productos cruzados con valores vectoriales no triviales de dos vectores en otras dimensiones está relacionada con el resultado del teorema de Hurwitz de que las únicas álgebras de división normadas son las de dimensión 1, 2, 4 y 8.

Producto exterior

En dimensión general, no existe un análogo directo del producto cruzado binario que produzca específicamente un vector. Sin embargo, existe el producto exterior, que tiene propiedades similares, excepto que el producto exterior de dos vectores ahora es un 2-vector en lugar de un vector ordinario. Como se mencionó anteriormente, el producto vectorial puede interpretarse como el producto exterior en tres dimensiones mediante el uso del operador estrella de Hodge para mapear 2 vectores a vectores. El dual de Hodge del producto exterior produce un vector (n − 2), que es una generalización natural del producto vectorial en cualquier número de dimensiones.

El producto exterior y el producto escalar se pueden combinar (a través de la suma) para formar el producto geométrico en álgebra geométrica.

Producto externo

Como se mencionó anteriormente, el producto vectorial puede interpretarse en tres dimensiones como el dual de Hodge del producto exterior. En cualquier dimensión n finita, el dual de Hodge del producto exterior de los vectores n − 1 es un vector. Entonces, en lugar de una operación binaria, en dimensiones finitas arbitrarias, el producto vectorial se generaliza como el dual de Hodge del producto exterior de algún n − 1 vectores. Esta generalización se llama producto externo.

Producto conmutador

Interpretando el espacio vectorial tridimensional del álgebra como el subalgebra de 2-vector (no el 1-vector) del álgebra geométrica tridimensional, donde ${displaystyle mathbf {i} =mathbf {e_{2}} mathbf {e_{3}} }$ , ${displaystyle mathbf {j} =mathbf {e_{1}} mathbf {e_{3}} }$ , y ${displaystyle mathbf {k} =mathbf {e_{1}} mathbf {e_{2}} }$ , el producto de la cruz corresponde exactamente al producto del conmutador en álgebra geométrica y ambos utilizan el mismo símbolo $times$ . El producto conmutador se define para 2-vectores $A$ y $B$ en álgebra geométrica como:

{displaystyle Atimes B={tfrac {1}{2}}(AB-BA)}

Donde $AB$ es el producto geométrico.

El producto del conmutador podría generalizarse a multivectores arbitrarios en tres dimensiones, lo que da como resultado un multivector que consiste solo en elementos de grados 1 (1-vectores/vectores verdaderos) y 2 (2-vectores/pseudovectores). Mientras que el producto conmutador de dos vectores 1 es de hecho el mismo que el producto exterior y produce un vector 2, el conmutador de un vector 1 y un vector 2 produce un vector verdadero, que corresponde en cambio a las contracciones izquierda y derecha en álgebra geométrica. El producto conmutador de dos 2 vectores no tiene un producto equivalente correspondiente, por lo que el producto conmutador se define en primer lugar para 2 vectores. Además, el producto triple del conmutador de tres 2 vectores es el mismo que el producto triple vectorial de los mismos tres pseudovectores en álgebra vectorial. Sin embargo, el producto triple del conmutador de tres vectores 1 en álgebra geométrica es, en cambio, el negativo del producto triple vectorial de los mismos tres vectores verdaderos en álgebra vectorial.

Las generalizaciones a dimensiones superiores las proporciona el mismo producto conmutador de 2 vectores en álgebras geométricas de dimensiones superiores, pero los 2 vectores ya no son pseudovectores. Así como el producto conmutador/producto cruzado de 2 vectores en tres dimensiones corresponde al álgebra de Lie más simple, las subálgebras de 2 vectores del álgebra geométrica de dimensiones superiores equipadas con el producto conmutador también corresponden a las álgebras de Lie. También como en tres dimensiones, el producto del conmutador podría generalizarse aún más a multivectores arbitrarios.

Álgebra multilineal

En el contexto del álgebra multilineal, el producto vectorial puede verse como el tensor (1,2) (un tensor mixto, específicamente un mapa bilineal) obtenido de la forma de volumen tridimensional, un (0,3) -tensor, elevando un índice.

En detalle, la forma de volumen tridimensional define un producto ${displaystyle Vtimes Vtimes Vto mathbf {R}}$ tomando el determinante de la matriz dada por estos 3 vectores. Por dualidad, esto equivale a una función ${displaystyle Vtimes Vto V^{*},}$ (Fijar dos entradas da una función ${displaystyle Vto mathbf {R} }$ evaluando sobre la tercera entrada) y en presencia de un producto interno (como el producto del punto; más generalmente, una forma bilineal no degenerada), tenemos un isomorfismo ${displaystyle Vto V^{*},}$ y así esto produce un mapa ${displaystyle Vtimes Vto V,}$ que es el producto de la cruz: un (0,3)-tensor (3 entradas vectoriales, salida del escalar) se ha transformado en un (1,2)-tensor (2 entradas vectoriales, 1 salida vectorial) por "alzar un índice".

Traducir el álgebra anterior a la geometría, la función "volumen del paralelo definido por ${displaystyle (a,b,-)}$ " (donde se fijan los dos primeros vectores y el último es una entrada), que define una función ${displaystyle Vto mathbf {R} }$ , puede ser representado único como el producto de punto con un vector: este vector es el producto de la cruz ${displaystyle atimes b.}$ Desde esta perspectiva, el producto cruzado es definida por el producto triple del cuero cabelludo, ${displaystyle mathrm {Vol} (a,b,c)=(atimes b)cdot c.}$

Del mismo modo, en dimensiones superiores se puede definir los productos cruzados generalizados al elevar índices de los n-forma de volumen dimensional, que es un ${displaystyle (0,n)}$ -tensor. Las generalizaciones más directas del producto de la cruz son para definir:

a ${displaystyle (1,n-1)}$ -tensor, que toma como entrada ${displaystyle n-1}$ vectores, y da como resultado 1 vector – un ${displaystyle (n-1)}$ - producto de valor vectorial diario, o
a ${displaystyle (n-2,2)}$ -tensor, que toma como entrada 2 vectores y da como tensor simétrico de salida de la clase n − 2 – un producto binario con rango n − 2 Valores tensores. También se puede definir $(k,n-k)$ -tensores para otros k.

Estos productos son todos multilineales y asimétricos, y se pueden definir en términos de determinante y paridad.

El ${displaystyle (n-1)}$ - El producto diario se puede describir como sigue: ${displaystyle n-1}$ vectores ${displaystyle v_{1},dotsv_{n-1}}$ dentro $mathbf {R} ^{n},$ definir su producto transversal generalizado ${displaystyle v_{n}=v_{1}times cdots times v_{n-1}}$ como:

perpendicular al hiperplano definido por el ${displaystyle v_{i},}$
magnitud es el volumen del paraleloótopo definido por el ${displaystyle v_{i},}$ que se puede calcular como el determinante de Gram del ${displaystyle v_{i},}$
orientado para que ${displaystyle v_{1},dotsv_{n}}$ está positivamente orientado.

Este es el único producto multilineal, alternador que evalúa ${displaystyle e_{1}times cdots times e_{n-1}=e_{n}}$ , ${displaystyle e_{2}times cdots times e_{n}=e_{1},}$ y así sucesivamente para permutaciones cíclicas de índices.

En coordenadas, se puede dar una fórmula para esto ${displaystyle (n-1)}$ - análogo diario del producto de la cruz en Rⁿ por:

{displaystyle bigwedge _{i=0}^{n-1}mathbf {v} _{i}={begin{vmatrix}v_{1}{}^{1}&cdots &v_{1}{}^{n}\vdots &ddots &vdots \v_{n-1}{}^{1}&cdots &v_{n-1}{}^{n}\mathbf {e} _{1}&cdots &mathbf {e} _{n}end{vmatrix}}.}

Esta fórmula es idéntica en la estructura a la fórmula determinante para el producto transversal normal en R³ excepto que la fila de vectores de base es la última fila en el determinante en lugar de la primera. La razón de esto es asegurar que los vectores ordenados (v₁,... v_n−1, véase^n–1
_i=0v_i) tienen una orientación positiva con respecto a (e₁,... e_n). Si n es extraño, esta modificación deja el valor sin cambios, por lo que esta convención está de acuerdo con la definición normal del producto binario. En caso de que n es incluso, sin embargo, la distinción debe mantenerse. Esto ${displaystyle (n-1)}$ - La forma de diario disfruta de muchas de las mismas propiedades que el producto de la cruz vectorial: se alterna y lineal en sus argumentos, es perpendicular a cada argumento, y su magnitud da el hipervolumen de la región ligada por los argumentos. Y al igual que el producto de la cruz vectorial, se puede definir de forma independiente como el doble Hodge del producto de cuña de los argumentos. Además, el producto ${displaystyle [v_{1},ldotsv_{n}]:=bigwedge _{i=0}^{n}v_{i}}$ satisfice la identidad Filippov,

{displaystyle [[x_{1},ldotsx_{n}],y_{2},ldotsy_{n}]]=sum _{i=1}^{n}[x_{1},ldotsx_{i-1},[x_{i},y_{2},ldotsy_{n}],x_{i+1},ldotsx_{n}],}

y entonces dota a Rⁿ⁺¹ con una estructura de álgebra de n-Lie (ver Proposición 1 de).

Historia

En 1773, Joseph-Louis Lagrange utilizó la forma componente de los productos punto y cruz para estudiar el tetraedro en tres dimensiones.

En 1843, William Rowan Hamilton introdujo el producto de cuaterniones, y con él los términos vector y escalar. Dados dos cuaterniones [0, u] y [0, v], donde u y v son vectores en R³, su producto de cuaterniones se puede resumir como [−u ⋅ v, u × v]. James Clerk Maxwell usó las herramientas de cuaterniones de Hamilton para desarrollar sus famosas ecuaciones de electromagnetismo, y por esta y otras razones, los cuaterniones durante un tiempo fueron una parte esencial de la educación física.

En 1844, Hermann Grassmann publicó un álgebra geométrica no ligada a la dimensión dos o tres. Grassmann desarrolla varios productos, incluido un producto cruzado representado entonces por $[uv]$ . (Ver también: álgebra exterior.)

En 1853, Augustin-Louis Cauchy, contemporáneo de Grassmann, publicó un artículo sobre claves algebraicas que se usaban para resolver ecuaciones y tenían las mismas propiedades de multiplicación que el producto vectorial.

En 1878, William Kingdon Clifford publicó Elements of Dynamic, en el que se atestigua el término producto vectorial. En el libro, se define que este producto de dos vectores tiene una magnitud igual al área del paralelogramo del que son dos lados y una dirección perpendicular a su plano. (Ver también: Álgebra de Clifford.)

En 1881 notas de conferencias, Gibbs representa el producto cruzado por ${displaystyle utimes v}$ y lo llama producto. En 1901, el estudiante de Gibb Edwin Bidwell Wilson edita y extiende estas notas de conferencia en el libro de texto Vector Analysis. Wilson mantiene el término producto, pero observa que los términos alternativos producto cruzado y producto vectorial eran más frecuentes.

En 1908, Cesare Burali-Forti y Roberto Marcolongo presentan la notación del producto vectorial $U \land v$ . Esto se utiliza en Francia y otras áreas hasta hoy, como símbolo $times$ ya se utiliza para denotar la multiplicación y el producto cartesiano.

Contenido relacionado

Más resultados...