Proceso isentrópico

ImprimirCitar

Proceso termodinámico reversible y adiabático

En termodinámica, un proceso isentrópico es un proceso termodinámico idealizado que es adiabático y reversible. Las transferencias de trabajo del sistema no tienen fricción y no hay transferencia neta de calor o materia. Un proceso idealizado de este tipo es útil en ingeniería como modelo y base de comparación para procesos reales. Este proceso está idealizado porque en la realidad no ocurren procesos reversibles; pensar en un proceso como adiabático y reversible mostraría que las entropías inicial y final son las mismas, por eso se llama isentrópico (la entropía no cambia). Los procesos termodinámicos se denominan según el efecto que tendrían en el sistema (por ejemplo, isovolumétricos: volumen constante, isentálpicos: entalpía constante). Aunque en realidad no es necesariamente posible llevar a cabo un proceso isentrópico, algunos pueden aproximarse como tales.

La palabra "isentrópica" Puede interpretarse de otra manera, ya que su significado se deduce de su etimología. Significa un proceso en el que la entropía del sistema permanece sin cambios; Como se mencionó, esto podría ocurrir si el proceso es adiabático y reversible. Sin embargo, esto también podría ocurrir en un sistema donde el trabajo realizado sobre el sistema incluye fricción interna al sistema y se extrae calor del sistema en la cantidad justa para compensar la fricción interna, de modo que la entropía no cambie. Sin embargo, en relación con el universo, la entropía del universo aumentaría como resultado, de acuerdo con la Segunda Ley de la Termodinámica.

Fondo

La segunda ley de la termodinámica establece que

{displaystyle T_{text{surr}}dSgeq delta Q,}

Donde $delta Q$ es la cantidad de energía que el sistema gana por la calefacción, ${displaystyle T_{text{surr}}}$ es la temperatura del entorno, y $dS$ es el cambio en la entropía. El signo igual se refiere a un proceso reversible, que es un límite teórico idealizado imaginado, que nunca ocurre en realidad física, con temperaturas esencialmente iguales de sistema y entorno. Para un proceso isentrópico, si también es reversible, no hay transferencia de energía como calor porque el proceso es adiabático; δQ En cambio, si el proceso es irreversible, la entropía se produce dentro del sistema; en consecuencia, para mantener la entropía constante dentro del sistema, la energía debe ser eliminada simultáneamente del sistema como calor.

Para procesos reversibles, se lleva a cabo una transformación isentrópica "aislando&#34 térmicamente; el sistema de su entorno. La temperatura es la variable termodinámica conjugada de la entropía, por lo que el proceso conjugado sería un proceso isotérmico, en el que el sistema está térmicamente "conectado" a un baño térmico a temperatura constante.

Procesos isentrópicos en sistemas termodinámicos

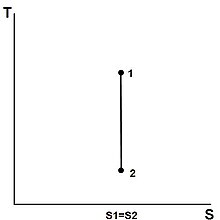
T–s (entropía vs. temperatura) diagrama de un proceso isentrópico, que es un segmento de línea vertical

La entropía de una masa dada no cambia durante un proceso que es reversible internamente y adiabático. Un proceso durante el cual la entropía permanece constante se llama un proceso istrópico, escrito ${displaystyle Delta s=0}$ o $s_{1}=s_{2}$ . Algunos ejemplos de dispositivos termodinámicos teóricamente istrópicos son bombas, compresores de gas, turbinas, boquillas y difusores.

Eficiencias isentrópicas de dispositivos de flujo estacionario en sistemas termodinámicos

La mayoría de los dispositivos de flujo estacionario funcionan en condiciones adiabáticas y el proceso ideal para estos dispositivos es el proceso isentrópico. El parámetro que describe la eficiencia con la que un dispositivo se aproxima a un dispositivo isentrópico correspondiente se denomina eficiencia isentrópica o adiabática.

Eficiencia isentrópica de turbinas:

{displaystyle eta _{text{t}}={frac {text{actual turbine work}}{text{isentropic turbine work}}}={frac {W_{a}}{W_{s}}}cong {frac {h_{1}-h_{2a}}{h_{1}-h_{2s}}}.}

Eficiencia isentrópica de compresores:

{displaystyle eta _{text{c}}={frac {text{isentropic compressor work}}{text{actual compressor work}}}={frac {W_{s}}{W_{a}}}cong {frac {h_{2s}-h_{1}}{h_{2a}-h_{1}}}.}

Eficiencia isentrópica de boquillas:

{displaystyle eta _{text{n}}={frac {text{actual KE at nozzle exit}}{text{isentropic KE at nozzle exit}}}={frac {V_{2a}^{2}}{V_{2s}^{2}}}cong {frac {h_{1}-h_{2a}}{h_{1}-h_{2s}}}.}

Para todas las ecuaciones anteriores:

h_{1}

es el enthalpy específico en el estado de entrada,

h_{2a}

es el enthalpy específico en el estado de salida para el proceso real,

h_{2s}

es el enthalpy específico en el estado de salida para el proceso istrópico.

Dispositivos isentrópicos en ciclos termodinámicos

Ciclo	Isentropic step	Descripción
Ciclo ideal Rankine	1→2	Compresión istrópica en una bomba
Ciclo ideal Rankine	3→4	Ampliación Isentrópica en una turbina
Ciclo ideal de carnot	2→3	Isentropic expansion
Ciclo ideal de carnot	4→1	Compresión sensorial
Ciclo ideal de Otto	1→2	Compresión sensorial
Ciclo ideal de Otto	3→4	Isentropic expansion
Ciclo diesel ideal	1→2	Compresión sensorial
Ciclo diesel ideal	3→4	Isentropic expansion
Ciclo de Brayton ideal	1→2	Compresión istrópica en un compresor
Ciclo de Brayton ideal	3→4	Ampliación Isentrópica en una turbina
Ciclo de refrigeración ideal para la compresión de vapor	1→2	Compresión istrópica en un compresor
ciclo de Lenoir ideal	2→3	Isentropic expansion

Nota: Los supuestos isentrópicos solo son aplicables con ciclos ideales. Los ciclos reales tienen pérdidas inherentes debido a ineficiencias del compresor y la turbina y a la segunda ley de la termodinámica. Los sistemas reales no son verdaderamente isentrópicos, pero el comportamiento isentrópico es una aproximación adecuada para muchos propósitos de cálculo.

Flujo isentrópico

En dinámica de fluidos, un flujo isentrópico es un flujo de fluido que es adiabático y reversible. Es decir, no se añade calor al flujo y no se producen transformaciones de energía debido a la fricción o efectos disipativos. Para un flujo isentrópico de un gas perfecto, se pueden derivar varias relaciones para definir la presión, densidad y temperatura a lo largo de una línea de corriente.

Tenga en cuenta que la energía puede intercambiarse con el flujo en una transformación isentrópica, siempre y cuando no ocurra como intercambio de calor. Un ejemplo de tal intercambio sería una expansión o compresión isentrópica que implica trabajo realizado sobre o por el flujo.

Para un flujo isentrópico, la densidad de entropía puede variar entre diferentes líneas de corriente. Si la densidad de entropía es la misma en todas partes, entonces se dice que el flujo es homentrópico.

Derivación de las relaciones isentrópicas

Para un sistema cerrado, el cambio total de energía de un sistema es la suma del trabajo realizado y el calor agregado:

{displaystyle dU=delta W+delta Q.}

El trabajo reversible realizado en un sistema al cambiar el volumen es

{displaystyle delta W=-p,dV,}

Donde $p$ es la presión, y $V$ es el volumen. El cambio en la enthalpy ( $H=U+pV$ ) es dado por

{displaystyle dH=dU+p,dV+V,dp.}

Entonces para un proceso que es tanto reversible como adiabático (es decir, no se produce transferencia de calor), ${displaystyle delta Q_{text{rev}}=0}$ , y así ${displaystyle dS=delta Q_{text{rev}}/T=0}$ Todos los procesos adiabáticos reversibles son istrópicos. Esto lleva a dos observaciones importantes:

{displaystyle dU=delta W+delta Q=-p,dV+0,}

{displaystyle dH=delta W+delta Q+p,dV+V,dp=-p,dV+0+p,dV+V,dp=V,dp.}

A continuación, se pueden calcular muchas cosas para procesos isentrópicos de un gas ideal. Para cualquier transformación de un gas ideal, siempre es cierto que

{displaystyle dU=nC_{v},dT}

, y

{displaystyle dH=nC_{p},dT.}

Utilización de los resultados generales derivados anteriormente $dU$ y $dH$ , entonces

{displaystyle dU=nC_{v},dT=-p,dV,}

{displaystyle dH=nC_{p},dT=V,dp.}

Entonces, para un gas ideal, la relación de capacidad calorífica se puede escribir como

{displaystyle gamma ={frac {C_{p}}{C_{V}}}=-{frac {dp/p}{dV/V}}.}

Para un gas calóricamente perfecto $gamma$ es constante. De ahí en la integración de la ecuación anterior, asumiendo un gas calóricamente perfecto, obtenemos

{displaystyle pV^{gamma }={text{constant}},}

es decir,

{displaystyle {frac {p_{2}}{p_{1}}}=left({frac {V_{1}}{V_{2}}}right)^{gamma }.}

Usando la ecuación de estado para un gas ideal, ${displaystyle pV=nRT}$ ,

{displaystyle TV^{gamma -1}={text{constant}}.}

(Proof: ${displaystyle PV^{gamma }={text{constant}}Rightarrow PV,V^{gamma -1}={text{constant}}Rightarrow nRT,V^{gamma -1}={text{constant}}.}$ Pero... NR = constante en sí mismo, así que ${displaystyle TV^{gamma -1}={text{constant}}}$ .)

{displaystyle {frac {p^{gamma -1}}{T^{gamma }}}={text{constant}}}

también, por constante $C_{p}=C_{v}+R$ (por topo),

{frac {V}{T}}={frac {nR}{p}}

p={frac {nRT}{V}}

S_{2}-S_{1}=nC_{p}ln left({frac {T_{2}}{T_{1}}}right)-nRln left({frac {p_{2}}{p_{1}}}right)

{frac {S_{2}-S_{1}}{n}}=C_{p}ln left({frac {T_{2}}{T_{1}}}right)-Rln left({frac {T_{2}V_{1}}{T_{1}V_{2}}}right)=C_{v}ln left({frac {T_{2}}{T_{1}}}right)+Rln left({frac {V_{2}}{V_{1}}}right)

Así, para procesos isentrópicos con un gas ideal,

T_{2}=T_{1}left({frac {V_{1}}{V_{2}}}right)^{(R/C_{v})}

V_{2}=V_{1}left({frac {T_{1}}{T_{2}}}right)^{(C_{v}/R)}

Tabla de relaciones isentrópicas para un gas ideal

${frac {T_{2}}{T_{1}}}$	$=$	${displaystyle left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}}$	$=$	$left({frac {V_{1}}{V_{2}}}right)^{(gamma -1)}$	$=$	$left({frac {rho _{2}}{rho _{1}}}right)^{(gamma -1)}$
$left({frac {T_{2}}{T_{1}}}right)^{frac {gamma }{gamma -1}}$	$=$	${displaystyle {frac {P_{2}}{P_{1}}}}$	$=$	$left({frac {V_{1}}{V_{2}}}right)^{gamma }$	$=$	$left({frac {rho _{2}}{rho _{1}}}right)^{gamma }$
$left({frac {T_{1}}{T_{2}}}right)^{frac {1}{gamma -1}}$	$=$	${displaystyle left({frac {P_{1}}{P_{2}}}right)^{frac {1}{gamma }}}$	$=$	${frac {V_{2}}{V_{1}}}$	$=$	${frac {rho _{1}}{rho _{2}}}$
$left({frac {T_{2}}{T_{1}}}right)^{frac {1}{gamma -1}}$	$=$	${displaystyle left({frac {P_{2}}{P_{1}}}right)^{frac {1}{gamma }}}$	$=$	${frac {V_{1}}{V_{2}}}$	$=$	${frac {rho _{2}}{rho _{1}}}$