Proceso gaussiano

En teoría de probabilidad y estadística, un proceso gaussiano es un proceso estocástico (una colección de variables aleatorias indexadas por tiempo o espacio), tal que cada colección finita de esas variables aleatorias tiene una distribución normal multivariante, es decir, toda combinación lineal finita de ellos se distribuye normalmente. La distribución de un proceso gaussiano es la distribución conjunta de todas esas (infinitas) variables aleatorias y, como tal, es una distribución sobre funciones con un dominio continuo, p. tiempo o espacio.

El concepto de procesos gaussianos lleva el nombre de Carl Friedrich Gauss porque se basa en la noción de distribución gaussiana (distribución normal). Los procesos gaussianos pueden verse como una generalización de dimensión infinita de distribuciones normales multivariadas.

Los procesos gaussianos son útiles en el modelado estadístico y se benefician de las propiedades heredadas de la distribución normal. Por ejemplo, si un proceso aleatorio se modela como un proceso gaussiano, las distribuciones de varias cantidades derivadas se pueden obtener explícitamente. Tales cantidades incluyen el valor promedio del proceso en un rango de tiempos y el error al estimar el promedio utilizando valores de muestra en un pequeño conjunto de tiempos. Si bien los modelos exactos a menudo se escalan de manera deficiente a medida que aumenta la cantidad de datos, se han desarrollado múltiples métodos de aproximación que a menudo conservan una buena precisión y reducen drásticamente el tiempo de cálculo.

Definición

Un proceso estocástico continuo de tiempo {}Xt;t▪ ▪ T}{displaystyle left{X_{t};tin Tright} es Gaussian si y sólo si por cada conjunto finito de índices t1,...... ,tk{displaystyle t_{1},ldotst_{k} in the index set T{displaystyle T}

Xt1,...... ,tk=()Xt1,...... ,Xtk){displaystyle mathbf {X} _{t_{1},ldotst_{k}=(X_{t_{1}}},ldotsX_{t_{k}) }

es una variable aleatoria gaissa multivariada. Eso es lo mismo que decir cada combinación lineal de ()Xt1,...... ,Xtk){displaystyle (X_{t_{1}},ldotsX_{t_{k}}} tiene una distribución normal (o gaissa) univariada.

Utilizando funciones características de variables aleatorias, la propiedad gaisiana se puede formular de la siguiente manera: {}Xt;t▪ ▪ T}{displaystyle left{X_{t};tin Tright} es Gaussian si y sólo si, por cada conjunto finito de índices t1,...... ,tk{displaystyle t_{1},ldotst_{k}, hay valor real σ σ l l j{displaystyle sigma _{ell j}, μ μ l l {displaystyle mu _{ell } con 0}" xmlns="http://www.w3.org/1998/Math/MathML">σ σ jj■0{displaystyle sigma _{jj} título0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8de9e3098c8961852a177f33ed0c6ea3d50f9845" style="vertical-align: -1.005ex; width:7.175ex; height:2.843ex;"/> tal que la siguiente igualdad sea válida para todos s1,s2,...... ,sk▪ ▪ R{displaystyle s_{1},s_{2},ldotss_{k}in mathbb {R}

E⁡ ⁡ ()exp⁡ ⁡ ()i.. l l =1ksl l Xtl l ))=exp⁡ ⁡ ()− − 12.. l l ,jσ σ l l jsl l sj+i.. l l μ μ l l sl l ),{displaystyle operatorname {E} left(exp left(isum _{ell =1}{k}s_{ell }mathbf {X} _{t_{ell }right)=exp left(-{frac {1}{2}sum _{ellj}sigma ¿Qué? J. }s_{j}+isum ¿Por qué? - Sí.

Donde i{displaystyle i} denota la unidad imaginaria tal que i2=− − 1{displaystyle I^{2}=-1}.

Los números σ σ l l j{displaystyle sigma _{ell j} y μ μ l l {displaystyle mu _{ell } se puede demostrar que son las covarianzas y los medios de las variables en el proceso.

Variación

La varianza de un proceso gaisiano es finita en cualquier momento t{displaystyle t}, formalmente

Estacionaria

Para procesos estocásticos generales, la estacionariedad en sentido estricto implica estacionariedad en sentido amplio, pero no todos los procesos estocásticos estacionarios en sentido amplio son estacionarios en sentido estricto. Sin embargo, para un proceso estocástico gaussiano los dos conceptos son equivalentes.

Un proceso estocástico gaussiano es estacionario en sentido estricto si, y solo si, es estacionario en sentido amplio.

Ejemplo

Existe una representación explícita para los procesos gaussianos estacionarios. Un ejemplo simple de esta representación es

Xt=#⁡ ⁡ ()at).. 1+pecado⁡ ⁡ ()at).. 2{displaystyle X_{t}=cos(at)xi _{1}+sin(at)xi _{2}

Donde .. 1{displaystyle xi _{1}} y .. 2{displaystyle xi _{2}} son variables aleatorias independientes con la distribución normal estándar.

Funciones de covarianza

Un hecho clave de los procesos gaussianos es que pueden definirse completamente por sus estadísticas de segundo orden. Por lo tanto, si se supone que un proceso gaussiano tiene media cero, la definición de la función de covarianza define completamente el proceso' comportamiento. Es importante destacar que la definición no negativa de esta función permite su descomposición espectral utilizando la expansión Karhunen-Loève. Los aspectos básicos que se pueden definir a través de la función de covarianza son el proceso' estacionariedad, isotropía, suavidad y periodicidad.

Estabilidad se refiere al comportamiento del proceso en relación con la separación de dos puntos x{displaystyle x} y x.{displaystyle x'}. Si el proceso es estacionario, la función de covariancia depende solamente de x− − x.{displaystyle x-x'}. Por ejemplo, el proceso Ornstein-Uhlenbeck es estacionario.

Si el proceso depende solamente de Silenciox− − x.Silencio{displaystyle Silencioso, la distancia euroclidiana (no la dirección) entre x{displaystyle x} y x.{displaystyle x'}, entonces el proceso se considera isotrópico. Se considera que un proceso simultáneamente estacionario e isotrópico es homogéneo; en la práctica estas propiedades reflejan las diferencias (o más bien la falta de ellas) en el comportamiento del proceso dado la ubicación del observador.

En última instancia, los procesos gaussianos se traducen como tomar prioridades en funciones y la suavidad de estos antecedentes puede ser inducida por la función de covariancia. Si esperamos que para los puntos de entrada "cerca a poco" x{displaystyle x} y x.{displaystyle x'} sus puntos de salida correspondientes Sí.{displaystyle y} y Sí..{displaystyle y'} para ser "cerca" también, entonces la suposición de continuidad está presente. Si deseamos permitir un desplazamiento significativo, entonces podríamos elegir una función de covariancia más difícil. Ejemplos extremos del comportamiento son la función de covariancia Ornstein-Uhlenbeck y el exponencial cuadrado donde el primero nunca es diferente y el último infinitamente diferente.

La periodicidad se refiere a inducir patrones periódicos dentro del comportamiento del proceso. Formally, esto se logra mediante la asignación de la entrada x{displaystyle x} a un vector bidimensional u()x)=()#⁡ ⁡ ()x),pecado⁡ ⁡ ()x)){displaystyle u(x)=left(cos(x),sin(x)right)}.

Funciones de covarianza habituales

Hay una serie de funciones de covarianza comunes:

• Constante: KC()x,x.)=C{displaystyle K_{operatorname {C}(x,x')=C}
• Linear: KL()x,x.)=xTx.{displaystyle K_{operatorname {L}(x,x')=x^{mathsf {T}x'}
• ruido gaisiano blanco: KGN()x,x.)=σ σ 2δ δ x,x.{displaystyle K_{operatorname {GN}(x,x')=sigma ^{2}delta _{x,x'}
• Exponencia cuadrada: KSE()x,x.)=exp⁡ ⁡ ()− − SilenciodSilencio22l l 2){displaystyle K_{operatorname {SE}(x,x')=exp left(-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}
• Ornstein-Uhlenbeck: KOU()x,x.)=exp⁡ ⁡ ()− − SilenciodSilenciol l ){displaystyle K_{operatorname {OU}(x,x')=exp left(-{frac {fc {fncipado en la vida}{ell }right)}
• Matérn: KMatern()x,x.)=21− − .. .. ().. )()2.. SilenciodSilenciol l ).. K.. ()2.. SilenciodSilenciol l ){displaystyle K_{ nombre del operador [Matern] }(x,x')={frac {2^{1nu {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ¿Por qué? - ¿Qué?
• Periódico: KP()x,x.)=exp⁡ ⁡ ()− − 2pecado2⁡ ⁡ ()d2)l l 2){displaystyle ¿Qué?
• Cuadrático racional: KRQ()x,x.)=()1+SilenciodSilencio2)− − α α ,α α ≥ ≥ 0{displaystyle K_{operatorname {RQ}(x,x')=left(1+ sobrevivido^{2}right)^{-alpha },quad alpha geq 0}

Aquí. d=x− − x.{displaystyle d=x-x}. El parámetro l l {displaystyle ell } es la escala de longitud característica del proceso (prácticamente, "qué cerca" dos puntos x{displaystyle x} y x.{displaystyle x'} tienen que ser influir uno al otro significativamente), δ δ {displaystyle delta } es el Kronecker delta y σ σ {displaystyle sigma } la desviación estándar de las fluctuaciones del ruido. Además, K.. {displaystyle K_{nu}} es la función Bessel modificada del orden .. {displaystyle nu } y .. ().. ){displaystyle Gamma (nu)} es la función gamma evaluada .. {displaystyle nu }. Importantemente, una complicada función de covariancia se puede definir como una combinación lineal de otras funciones de covariancia más simples para incorporar diferentes puntos de vista sobre el conjunto de datos a mano.

Los resultados inferenciales dependen de los valores de los hiperparametros Silencio Silencio {displaystyle theta } (por ejemplo. l l {displaystyle ell } y σ σ {displaystyle sigma }) definiendo el comportamiento del modelo. Una opción popular para Silencio Silencio {displaystyle theta } is to provide máximo a posteriori (MAP) estimaciones de ello con algunos elegidos antes. Si el anterior es muy uniforme, esto es lo mismo que maximizar la probabilidad marginal del proceso; la marginación que se hace sobre los valores de proceso observados Sí.{displaystyle y}. This approach is also known as máxima probabilidad II, maximización de las pruebas, o Bahías empíricas.

Continuidad

Para un proceso gaussiano, la continuidad en la probabilidad es equivalente a la continuidad cuadrática media, y la continuidad con probabilidad uno es equivalente a la continuidad muestral. Este último implica, pero no está implicado por, la continuidad en la probabilidad. La continuidad en la probabilidad se cumple si y solo si la media y la autocovarianza son funciones continuas. Por el contrario, la continuidad de la muestra fue un desafío incluso para los procesos gaussianos estacionarios (como probablemente señaló primero Andrey Kolmogorov), y más desafiante para los procesos más generales. Como es habitual, por proceso muestral continuo se entiende un proceso que admite una modificación muestral continua.

Estuche estacionario

Para un proceso de Gaussian estacionario X=()Xt)t▪ ▪ R,{displaystyle X=(X_{t})_{tin mathbb {R},} algunas condiciones en su espectro son suficientes para la continuidad de la muestra, pero no son necesarias. Una condición necesaria y suficiente, a veces llamada teorema Dudley-Fernique, implica la función σ σ {displaystyle sigma } definidas por

σ σ ()h)=E()X()t+h)− − X()t))2{displaystyle sigma (h)={sqrt {mathbb {E} {big (}X(t+h)-X(t){big)}}}}}}}

t{displaystyle t}

X{displaystyle X}

σ σ {displaystyle sigma }

0.{displaystyle 0.}

σ σ ()h){displaystyle sigma (h)}

0{displaystyle 0}

h→ → 0{displaystyle hto 0}

X{displaystyle X}

I()σ σ )=∫ ∫ 01σ σ ()h)hlog⁡ ⁡ ()1/h)dh=∫ ∫ 0JUEGO JUEGO 2σ σ ()e− − x2)dx,{displaystyle I(sigma)=int _{0}{1}{frac {sigma (h)}{h{sqrt {log(1/h)}}},dh=int #2sigma (e^{-x^{2}),dx,}

h=e− − x2,{textstyle h=e^{-x^{2}}}

x=log⁡ ⁡ ()1/h).{textstyle x={sqrt {log(1/h)}}

h→ → 0+,{displaystyle hto 0+,}

I()σ σ )=JUEGO JUEGO {displaystyle I(sigma)=infty }

σ σ ()e− − x2)=1xa{textstyle sigma (e^{-x^{2}})={tfrac {1}{x^{a}}}}

x,{displaystyle x,}

σ σ ()h)=()log⁡ ⁡ ()1/h))− − a/2{textstyle sigma (h)=(log(1/h)^{-a/2}

h,{displaystyle h,}

1,}" xmlns="http://www.w3.org/1998/Math/MathML">a■1,{displaystyle a confía1,}1," aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1748da13cbfe2011c831ffe06f5fcc8c1b986fa0" style="vertical-align: -0.671ex; width:6.138ex; height:2.509ex;"/>

I()σ σ )=JUEGO JUEGO {displaystyle I(sigma)=infty }

σ σ {displaystyle sigma }

[0,JUEGO JUEGO ),{displaystyle [0,infty]

(*) existe 0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/> tales que σ σ {displaystyle sigma } es monotono encendido [0,ε ε ]{displaystyle [0,varepsilon]

no sigue de la continuidad de σ σ {displaystyle sigma } y las relaciones evidentes σ σ ()h)≥ ≥ 0{displaystyle sigma (h)geq 0} (para todos) h{displaystyle h}) y σ σ ()0)=0.{displaystyle sigma (0)=0.}

Algo de historia. La suficiencia fue anunciada por Xavier Fernique en 1964, pero la primera prueba fue publicada por Richard M. Dudley en 1967. La necesidad fue probada por Michael B. Marcus y Lawrence Shepp en 1970.

Existen procesos continuos de muestra X{displaystyle X} tales que I()σ σ )=JUEGO JUEGO ;{displaystyle I(sigma)=infty;} violan las condiciones (*). Un ejemplo encontrado por Marcus y Shepp es una serie aleatoria de Fourier

Xt=.. n=1JUEGO JUEGO cn().. n#⁡ ⁡ λ λ nt+.. npecado⁡ ⁡ λ λ nt),{displaystyle X_{t}=sum _{n=1}{infty }c_{n}(xi _{n}cos lambda _{n}t+eta _{n}sin lambda _{n}t),}

.. 1,.. 1,.. 2,.. 2,...... {displaystyle xi _{1},eta _{1},xi _{2},eta _{2},dots }

0}" xmlns="http://www.w3.org/1998/Math/MathML">cn■0{displaystyle c_{n} {}}}}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2bad48de7e3ff5a22e32b25d39f0b878cff56a4c" style="vertical-align: -0.671ex; width:6.486ex; height:2.509ex;"/>

X.{displaystyle X.}

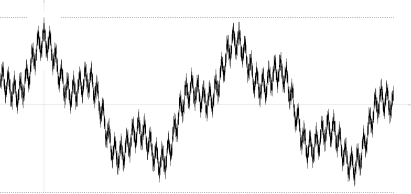
It's autocorrelation function

EXtXt+h=.. n=1JUEGO JUEGO cn2#⁡ ⁡ λ λ nh{displaystyle mathbb [E] ¿Qué? }c_{n} {2}cos lambda _{n}h}

σ σ ,{displaystyle sigma}

σ σ ()h)=2EXtXt− − 2EXtXt+h=2.. n=1JUEGO JUEGO cn2pecado2⁡ ⁡ λ λ nh2.{displaystyle sigma (h)={sqrt {2mathbb {E} X_{t}X_{t}-2mathbb ¿Qué? ¿Qué? }c_{n} {2}sin ^{2}{frac {fnMicrode - Sí.

Movimiento browniano como integral de procesos gaussianos

Un proceso de Wiener (también conocido como movimiento browniano) es la integral de un proceso gaussiano generalizado de ruido blanco. No es estacionario, pero tiene incrementos estacionarios.

El proceso de Ornstein-Uhlenbeck es un proceso gaussiano estacionario.

El puente browniano es (como el proceso de Ornstein-Uhlenbeck) un ejemplo de un proceso gaussiano cuyos incrementos no son independientes.

El movimiento browniano fraccional es un proceso gaussiano cuya función de covarianza es una generalización de la del proceso de Wiener.

Driscoll 's zero-one law

Driscoll 's zero-one law is a result characterizing the sample functions generated by a Gaussian process.

Vamos f{displaystyle f} ser un proceso medio-cero Gausiano {}Xt;t▪ ▪ T}{displaystyle left{X_{t};tin Tright} con función de covariancia definida no negativa K{displaystyle K}. Vamos H()R){displaystyle {Mathcal}(R)} ser un núcleo reproductor Hilbert espacio con núcleo definido positivo R{displaystyle R..

Entonces

Kn{displaystyle K_{n}

Rn{displaystyle R_{n}

n{displaystyle n}

Pr[f▪ ▪ H()R)]=1.{displaystyle Pr[fin {mathcal {H}(R)}=1.}

Además,

limn→ → JUEGO JUEGO tr⁡ ⁡ [KnRn− − 1]=JUEGO JUEGO {displaystyle lim _{nto infty}operatorname {tr} [K_{n}R_{n} {-1}=infty

Pr[f▪ ▪ H()R)]=0.{displaystyle Pr[fin {mathcal {H}(R)]=0.}

Esto tiene consecuencias significativas cuando K=R{displaystyle K=R., como

limn→ → JUEGO JUEGO tr⁡ ⁡ [RnRn− − 1]=limn→ → JUEGO JUEGO tr⁡ ⁡ [I]=limn→ → JUEGO JUEGO n=JUEGO JUEGO .{displaystyle lim _{nto infty}operatorname {tr} [R_{n}R_{-1}=lim _{nto infty }operatorname {tr} [I]=lim _{nto infty }n=infty.}

Como tal, casi todos los caminos de muestra de un proceso media-cero Gaussiano con el núcleo definido positivo K{displaystyle K} se quedará fuera del espacio de Hilbert H()K){displaystyle {Mathcal}(K)}.

Procesos gaussianos con restricciones lineales

Para muchas aplicaciones de interés, ya se proporciona algún conocimiento preexistente sobre el sistema en cuestión. Considere, por ejemplo, el caso donde la salida del proceso Gaussiano corresponde a un campo magnético; aquí, el campo magnético real está limitado por las ecuaciones de Maxwell y sería deseable una forma de incorporar esta restricción en el formalismo del proceso gaussiano, ya que esto probablemente mejoraría la precisión del algoritmo.

Ya existe un método sobre cómo incorporar restricciones lineales en procesos gaussianos:

Considere la función de salida (valorada por el actor) f()x){displaystyle f(x)} que se sabe que obedece la limitación lineal (es decir, FX{displaystyle {fnMithcal} {fnMicrosoft}} {fnMicrosoft}}} es un operador lineal)

FX()f()x))=0.{fnMicrosoft Sans Serif}=0.}

FX{displaystyle {fnMithcal} {fnMicrosoft}} {fnMicrosoft}}}

f()x)=GX()g()x)){displaystyle f(x)={mathcal {G}_{X}(g(x)}

g()x)♪ ♪ GP()μ μ g,Kg){displaystyle g(x)sim {mathcal}(mu _{g},K_{g})}

GX{displaystyle {Mathcal}_{X}}

FX()GX()g))=0О О g.{fnMicrosoft Sans} {fnMicrosoft Sans Serif} {G}_{X}(g)=0qquad forall g.}

GX{displaystyle {Mathcal}_{X}}

f{displaystyle f}

FX{displaystyle {fnMithcal} {fnMicrosoft}} {fnMicrosoft}}}

f()x)=GXg♪ ♪ GP()GXμ μ g,GXKgGX.T).{displaystyle f(x)={mathcal {G}_{X}gsim {fnMitcal} {fnMitcal} {G}_{X}mu _{g},{mathcal {G}_ {X}K_{g} {fnMitcal {G}_{X'} {Mathsf {T}}}

Aplicaciones

Se puede utilizar un proceso gaussiano como una distribución de probabilidad previa sobre funciones en la inferencia bayesiana. Dado cualquier conjunto de N puntos en el dominio deseado de sus funciones, tome una Gaussiana multivariada cuyo parámetro de matriz de covarianza sea la matriz de Gram de sus N puntos con algún núcleo deseado, y muestra de esa Gaussiana. Para la solución del problema de predicción de múltiples salidas, se desarrolló el proceso de regresión gaussiana para la función con valores vectoriales. En este método, un 'grande' se construye la covarianza, que describe las correlaciones entre todas las variables de entrada y salida tomadas en N puntos en el dominio deseado. Este enfoque se elaboró en detalle para los procesos gaussianos con valores matriciales y se generalizó a procesos con 'colas más pesadas' como los procesos Student-t.

La inferencia de valores continuos con un proceso gaussiano previo se conoce como regresión del proceso gaussiano o kriging; extender la regresión del proceso gaussiano a múltiples variables de destino se conoce como cokriging. Por lo tanto, los procesos gaussianos son útiles como una poderosa herramienta de interpolación multivariada no lineal.

Los procesos gaussianos también se usan comúnmente para abordar problemas de análisis numérico, como la integración numérica, la resolución de ecuaciones diferenciales o la optimización en el campo de la estadística numérica probabilística.

Los procesos gaussianos también se pueden usar en el contexto de una combinación de modelos expertos, por ejemplo. El fundamento subyacente de tal marco de aprendizaje consiste en la suposición de que un mapeo dado no puede ser bien capturado por un solo modelo de proceso gaussiano. En cambio, el espacio de observación se divide en subconjuntos, cada uno de los cuales se caracteriza por una función de mapeo diferente; cada uno de estos se aprende a través de un componente de proceso gaussiano diferente en la mezcla postulada.

En las ciencias naturales, los procesos gaussianos han encontrado uso como modelos probabilísticos de series temporales astronómicas y como predictores de propiedades moleculares.

Predicción de procesos gaussianos o Kriging

Cuando se trata de un problema general de regresión del proceso gaussiano (Kriging), se asume que para un proceso gaisiano f{displaystyle f} observadas en las coordenadas x{displaystyle x}, el vector de los valores f()x){displaystyle f(x)} es sólo una muestra de una distribución multivariada Gaussiana de dimensión igual al número de coordenadas observadas n{displaystyle n}. Por lo tanto, bajo el supuesto de una distribución de cero medios, f()x.)♪ ♪ N()0,K()Silencio Silencio ,x,x.)){displaystyle f(x')sim N(0,K(thetax,x')}, donde K()Silencio Silencio ,x,x.){displaystyle K(thetax,x)} es la matriz de covariancia entre todos los pares posibles ()x,x.){displaystyle (x,x)} para un determinado conjunto de hiperparametros Silencio. Como tal, la probabilidad marginal del tronco es:

log⁡ ⁡ p()f()x.)▪ ▪ Silencio Silencio ,x)=− − 12()f()x)TK()Silencio Silencio ,x,x.)− − 1f()x.)+log⁡ ⁡ Det()K()Silencio Silencio ,x,x.))+nlog⁡ ⁡ 2π π ){displaystyle log p(f(x')mid thetax)=-{frac {1}{2}left(f(x)^{mathsf {T}K(thetax,x')^{-1}f(x')+log det(K(thetax,x')))+nlog 2piright

y maximizar esta probabilidad marginal hacia Silencio proporciona la especificación completa del proceso gaussiano f. Se puede notar brevemente en este punto que el primer término corresponde a un plazo de penalización para que un modelo no se ajuste a los valores observados y el segundo término a un plazo de penalización que aumenta proporcionalmente a la complejidad de un modelo. Habiendo especificado Silencio, haciendo predicciones sobre valores no observados f()xAlternativa Alternativa ){displaystyle f(x^{*}} en coordenadas x* es entonces sólo una cuestión de extraer muestras de la distribución predictiva p()Sí.Alternativa Alternativa ▪ ▪ xAlternativa Alternativa ,f()x),x)=N()Sí.Alternativa Alternativa ▪ ▪ A,B){displaystyle p(y^{*}mid x^{*},f(x),x)=N(y^{*}mid A,B)} donde la estimación media posterior A se define como

A=K()Silencio Silencio ,xAlternativa Alternativa ,x)K()Silencio Silencio ,x,x.)− − 1f()x){displaystyle A=K(thetax^{*},x)K(thetax,x')^{-1}f(x)}

B=K()Silencio Silencio ,xAlternativa Alternativa ,xAlternativa Alternativa )− − K()Silencio Silencio ,xAlternativa Alternativa ,x)K()Silencio Silencio ,x,x.)− − 1K()Silencio Silencio ,xAlternativa Alternativa ,x)T{displaystyle B=K(thetax^{*},x^{*})-K(thetax^{*},x)K(thetax,x')^{-1}K(thetax^{*},x)^{mathsf {}}}}}}}}

K()Silencio Silencio ,xAlternativa Alternativa ,x){displaystyle K(thetax^{*},x)}

K()Silencio Silencio ,x,x.){displaystyle K(thetax,x)}

f()x){displaystyle f(x)}

K()Silencio Silencio ,xAlternativa Alternativa ,xAlternativa Alternativa ){displaystyle K(thetax^{*},x^{*}}

f()xAlternativa Alternativa ){displaystyle f(x^{*}}

f()x){displaystyle f(x)}

f()xAlternativa Alternativa ){displaystyle f(x^{*}}

f()x){displaystyle f(x)}

A menudo, la covariancia tiene la forma K()Silencio Silencio ,x,x.)=1σ σ 2K~ ~ ()Silencio Silencio ,x,x.){sigma ^{2}}{thetax,x')} {sigma ^{2}}{tilde {K}}(thetax,x')}, donde σ σ 2{displaystyle sigma ^{2} es un parámetro escalador. Ejemplos son las funciones de covariancia de clase Matérn. Si este parámetro escalar σ σ 2{displaystyle sigma ^{2} es conocido o desconocido (es decir, debe ser marginado), entonces la probabilidad posterior, p()Silencio Silencio ▪ ▪ D){displaystyle p(theta mid D)}, es decir, la probabilidad de los hiperparametros Silencio Silencio {displaystyle theta } dado un conjunto de pares de datos D{displaystyle D} of observations of x{displaystyle x} y f()x){displaystyle f(x)}, admite una expresión analítica.

Redes neuronales bayesianas como procesos gaussianos

Las redes neuronales bayesianas son un tipo particular de red bayesiana que resulta del tratamiento probabilístico de los modelos de redes neuronales artificiales y de aprendizaje profundo, y de la asignación de una distribución previa a sus parámetros. La computación en redes neuronales artificiales generalmente se organiza en capas secuenciales de neuronas artificiales. El número de neuronas en una capa se llama ancho de capa. A medida que crece el ancho de la capa, muchas redes neuronales bayesianas se reducen a un proceso gaussiano con un núcleo compositivo de forma cerrada. Este proceso gaussiano se denomina proceso gaussiano de red neuronal (NNGP). Permite que las predicciones de las redes neuronales bayesianas se evalúen de manera más eficiente y proporciona una herramienta analítica para comprender los modelos de aprendizaje profundo.

Problemas informáticos

En aplicaciones prácticas, los modelos de procesos gaussianos a menudo se evalúan en una cuadrícula que conduce a distribuciones normales multivariadas. El uso de estos modelos para la predicción o la estimación de parámetros utilizando la máxima verosimilitud requiere evaluar una densidad gaussiana multivariante, lo que implica calcular el determinante y el inverso de la matriz de covarianza. Ambas operaciones tienen una complejidad computacional cúbica, lo que significa que incluso para redes de tamaños modestos, ambas operaciones pueden tener un costo computacional prohibitivo. Este inconveniente condujo al desarrollo de múltiples métodos de aproximación.