Proceso de salchicha

ImprimirCitar

Proceso estocástico generalizando movimiento marroniano

Una sola realización de un proceso único de Wiener

Una sola realización de un proceso tridimensional de Wiener

En matemáticas, el proceso de Wiener es un proceso estocástico de tiempo continuo de valor real llamado así en honor al matemático estadounidense Norbert Wiener por sus investigaciones sobre las propiedades matemáticas del movimiento browniano unidimensional. A menudo también se le llama movimiento browniano debido a su conexión histórica con el proceso físico del mismo nombre observado originalmente por el botánico escocés Robert Brown. Es uno de los procesos de Lévy más conocidos (procesos estocásticos de càdlàg con incrementos independientes estacionarios) y ocurre con frecuencia en matemáticas puras y aplicadas, economía, finanzas cuantitativas, biología evolutiva y física.

El proceso de Wiener juega un papel importante tanto en las matemáticas puras como en las aplicadas. En matemáticas puras, el proceso de Wiener dio lugar al estudio de las martingalas de tiempo continuo. Es un proceso clave en términos del cual se pueden describir procesos estocásticos más complicados. Como tal, juega un papel vital en el cálculo estocástico, los procesos de difusión e incluso en la teoría potencial. Es el proceso impulsor de la evolución de Schramm-Loewner. En matemáticas aplicadas, el proceso de Wiener se utiliza para representar la integral de un proceso gaussiano de ruido blanco y, por lo tanto, es útil como modelo de ruido en ingeniería electrónica (ver ruido browniano), errores de instrumentos en la teoría de filtrado y perturbaciones en la teoría de control.

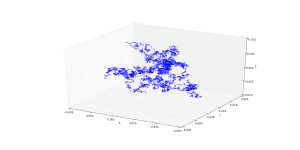
El proceso de Wiener tiene aplicaciones en todas las ciencias matemáticas. En física se utiliza para estudiar el movimiento browniano, la difusión de partículas diminutas suspendidas en un fluido y otros tipos de difusión a través de las ecuaciones de Fokker-Planck y Langevin. También forma la base para la formulación rigurosa de la integral de caminos de la mecánica cuántica (mediante la fórmula de Feynman-Kac, una solución a la ecuación de Schrödinger se puede representar en términos del proceso de Wiener) y el estudio de la inflación eterna en la cosmología física. También es prominente en la teoría matemática de las finanzas, en particular el modelo de valoración de opciones de Black-Scholes.

Caracterizaciones del proceso Wiener

El proceso de Wiener $W_{t}$ se caracteriza por las siguientes propiedades:

${displaystyle W_{0}=0}$
$W$ tiene incrementos independientes: por cada $0,}" xmlns="http://www.w3.org/1998/Math/MathML">t■0,{displaystyle t título0,}0,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c2159aad37e35b69930ad3b3afe15dab07ef52a4" style="vertical-align: -0.671ex; width:5.747ex; height:2.509ex;"/>$ los futuros incrementos ${displaystyle W_{t+u}-W_{t},}$ ${displaystyle ugeq 0,}$ son independientes de los valores anteriores $W_s$ , $<math alttext="{displaystyle ss.t.{displaystyle s wont.} <img alt="{displaystyle s$
$W$ tiene aumentos gaussianos: ${displaystyle W_{t+u}-W_{t}}$ se distribuye normalmente con media ${displaystyle 0}$ y diferencia $u$ , ${displaystyle W_{t+u}-W_{t}sim {mathcal {N}}(0,u).}$
$W$ tiene caminos continuos: $W_{t}$ es continuo $t$ .

Que el proceso tenga incrementos independientes significa que si $0 \leq s 1 < t 1 \leq s 2 < t 2$ luego $W t 1 - W s 1$ y W_t₂ − W_s₂ son variables aleatorias independientes, y la condición similar se cumple para incrementos de n.

Una caracterización alternativa del proceso de Wiener es la llamada caracterización de Lévy que dice que el proceso de Wiener es una martingala continua casi segura con $W 0 = 0$ y variación cuadrática $[W t, W t] = t$ (lo que significa que $W t 2 - t$ también es una martingala).

Una tercera caracterización es que el proceso de Wiener tiene una representación espectral como una serie sinusoidal cuyos coeficientes son variables aleatorias N(0, 1) independientes. Esta representación se puede obtener utilizando el teorema de Karhunen-Loève.

Otra caracterización de un proceso de Wiener es la integral definida (desde el tiempo cero hasta el tiempo t) de un proceso gaussiano de media cero, varianza unitaria, delta correlacionado ("blanco").

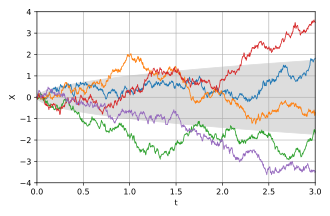
El proceso de Wiener se puede construir como el límite de escala de una caminata aleatoria u otros procesos estocásticos de tiempo discreto con incrementos independientes estacionarios. Esto se conoce como el teorema de Donsker. Al igual que el paseo aleatorio, el proceso de Wiener es recurrente en una o dos dimensiones (lo que significa que regresa casi con seguridad a cualquier vecindad fija del origen infinitamente a menudo) mientras que no es recurrente en dimensiones tres y superiores. A diferencia de la caminata aleatoria, es invariante de escala, lo que significa que

{displaystyle alpha ^{-1}W_{alpha ^{2}t}}

α

Medida Wiener

g

g (0) = 0

Wiener integral

Proceso de Wiener como límite de paseo aleatorio

Vamos ${displaystyle xi _{1},xi _{2},ldots }$ ser i.i.d. variables aleatorias con media 0 y varianza 1. Para cada uno n, definir un proceso estocástico de tiempo continuo

{displaystyle W_{n}(t)={frac {1}{sqrt {n}}}sum limits _{1leq kleq lfloor ntrfloor }xi _{k},qquad tin [0,1].}

W_{n}

xi _{k}

W_{n}(t)-W_{n}(s)

N(0,t-s)

nto infty

W_{n}

Propiedades de un proceso de Wiener unidimensional

Cinco procesos muestreados, con la desviación estándar prevista en gris.

Propiedades básicas

La función de densidad de probabilidad incondicional sigue una distribución normal con media = 0 y varianza = t, en un tiempo fijo $t$ :

{displaystyle f_{W_{t}}(x)={frac {1}{sqrt {2pi t}}}e^{-x^{2}/(2t)}.}

La expectativa es cero:

{displaystyle operatorname {E} [W_{t}]=0.}

La varianza, utilizando la fórmula computacional, es $t$ :

{displaystyle operatorname {Var} (W_{t})=t.}

Estos resultados se derivan inmediatamente de la definición de que los incrementos tienen una distribución normal, centrada en cero. De este modo

{displaystyle W_{t}=W_{t}-W_{0}sim N(0,t).}

Covarianza y correlación

La covariancia y correlación (donde $sleq t$ ):

{displaystyle {begin{aligned}operatorname {cov} (W_{s},W_{t})&=s,\operatorname {corr} (W_{s},W_{t})&={frac {operatorname {cov} (W_{s},W_{t})}{sigma _{W_{s}}sigma _{W_{t}}}}={frac {s}{sqrt {st}}}={sqrt {frac {s}{t}}}.end{aligned}}}

Estos resultados se derivan de la definición de que los incrementos no superpuestos son independientes, de los cuales sólo se utiliza la propiedad que no están relacionados. Supongamos que ${displaystyle t_{1}leq t_{2}}$ .

{displaystyle operatorname {cov} (W_{t_{1}},W_{t_{2}})=operatorname {E} left[(W_{t_{1}}-operatorname {E} [W_{t_{1}}])cdot (W_{t_{2}}-operatorname {E} [W_{t_{2}}])right]=operatorname {E} left[W_{t_{1}}cdot W_{t_{2}}right].}

Sustitución

{displaystyle W_{t_{2}}=(W_{t_{2}}-W_{t_{1}})+W_{t_{1}}}

{displaystyle {begin{aligned}operatorname {E} [W_{t_{1}}cdot W_{t_{2}}]&=operatorname {E} left[W_{t_{1}}cdot ((W_{t_{2}}-W_{t_{1}})+W_{t_{1}})right]\&=operatorname {E} left[W_{t_{1}}cdot (W_{t_{2}}-W_{t_{1}})right]+operatorname {E} left[W_{t_{1}}^{2}right].end{aligned}}}

Desde ${displaystyle W_{t_{1}}=W_{t_{1}}-W_{t_{0}}}$ y ${displaystyle W_{t_{2}}-W_{t_{1}}}$ son independientes,

{displaystyle operatorname {E} left[W_{t_{1}}cdot (W_{t_{2}}-W_{t_{1}})right]=operatorname {E} [W_{t_{1}}]cdot operatorname {E} [W_{t_{2}}-W_{t_{1}}]=0.}

Así

{displaystyle operatorname {cov} (W_{t_{1}},W_{t_{2}})=operatorname {E} left[W_{t_{1}}^{2}right]=t_{1}.}

Un corolario útil para la simulación es que podemos escribir, para $t 1 < t 2$ :

{displaystyle W_{t_{2}}=W_{t_{1}}+{sqrt {t_{2}-t_{1}}}cdot Z}

Z

Representación de Viena

Wiener (1923) también dio una representación de un camino marroniano en términos de una serie Fourier al azar. Si $xi _{n}$ son variables gaisianas independientes con media cero y varianza uno, entonces

{displaystyle W_{t}=xi _{0}t+{sqrt {2}}sum _{n=1}^{infty }xi _{n}{frac {sin pi nt}{pi n}}}

{displaystyle W_{t}={sqrt {2}}sum _{n=1}^{infty }xi _{n}{frac {sin left(left(n-{frac {1}{2}}right)pi tright)}{left(n-{frac {1}{2}}right)pi }}}

[0,1]

{displaystyle {sqrt {c}},Wleft({frac {t}{c}}right)}

[0,c]

Máxima corriente

La distribución conjunta del máximo móvil

{displaystyle M_{t}=max _{0leq sleq t}W_{s}}

W t

{displaystyle f_{M_{t},W_{t}}(m,w)={frac {2(2m-w)}{t{sqrt {2pi t}}}}e^{-{frac {(2m-w)^{2}}{2t}}},qquad mgeq 0,wleq m.}

Para obtener la distribución incondicional de $f_{M_{t}}$ , integrar sobre $♦ w \leq m$ :

{displaystyle {begin{aligned}f_{M_{t}}(m)&=int _{-infty }^{m}f_{M_{t},W_{t}}(m,w),dw=int _{-infty }^{m}{frac {2(2m-w)}{t{sqrt {2pi t}}}}e^{-{frac {(2m-w)^{2}}{2t}}},dw\[5pt]&={sqrt {frac {2}{pi t}}}e^{-{frac {m^{2}}{2t}}},qquad mgeq 0,end{aligned}}}

la función de densidad de probabilidad de una distribución seminormal. la expectativa es

{displaystyle operatorname {E} [M_{t}]=int _{0}^{infty }mf_{M_{t}}(m),dm=int _{0}^{infty }m{sqrt {frac {2}{pi t}}}e^{-{frac {m^{2}}{2t}}},dm={sqrt {frac {2t}{pi }}}}

Si a la vez $t$ el proceso de Wiener tiene un valor conocido ${displaystyle W_{t}}$ , es posible calcular la distribución de probabilidad condicional del máximo en intervalo $[0,t]$ (cf. Probability distribution of extreme points of a Wiener stochastic process). La función de distribución de probabilidad acumulativa del valor máximo, condicionada por el valor conocido $W_{t}$ , es:

max(0,W_{t})}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">FMWt()m)=Pr()MWt=max0≤ ≤ s≤ ≤ tW()s)≤ ≤ m▪ ▪ W()t)=Wt)=1− − e− − 2m()m− − Wt)t,m■max()0,Wt){displaystyle {fnMicrosoft Sans Serif} Pr left(M_{W_{t}=max _{0leq sleq t}W(s)leq mmid W(t)=W_{t}right)= 1- e^{-2{frac {m(m-W_{t} {t}\\,,\\ mmax(0,W_{t}}}max(0,W_{t})}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f9b8a944ce8e1c92899cf7e78bccd70cc2667950" style="vertical-align: -2.505ex; width:94.373ex; height:6.176ex;"/>

Autosimilitud

Una demostración de escalada de Brownian, mostrando

V_{t}=(1/{sqrt {c}})W_{ct}

para disminuir c. Tenga en cuenta que las características medias de la función no cambian mientras se amplía, y note que aumenta en forma horizontal cuadráticamente más rápida que verticalmente.

Escala browniana

Por todos $c ■ 0$ el proceso ${displaystyle V_{t}=(1/{sqrt {c}})W_{ct}}$ es otro proceso de Wiener.

Reversión del tiempo

El proceso $V_{t}=W_{1}-W_{1-t}$ para $0 \leq t \leq 1$ se distribuye como $W t$ para $0 \leq t \leq 1$ .

Inversión de tiempo

El proceso $V_{t}=tW_{1/t}$ es otro proceso de Wiener.

Una clase de martingalas brownianas

Si un polinomio $p (x, t)$ satisface la ecuación diferencial parcial

{displaystyle left({frac {partial }{partial t}}+{frac {1}{2}}{frac {partial ^{2}}{partial x^{2}}}right)p(x,t)=0}

{displaystyle M_{t}=p(W_{t},t)}

Ejemplo: $W_{t}^{2}-t$ es un martingale, que muestra que la variación cuadrática de W on $[0, t]$ es igual a $t$ . Se deduce que el tiempo previsto de la primera salida W de las Naciones Unidasc, c) es igual a $c 2$ .

Más generalmente, para cada polinomio $p (x, t)$ lo siguiente proceso estocástico es una martingala:

{displaystyle M_{t}=p(W_{t},t)-int _{0}^{t}a(W_{s},s),mathrm {d} s,}

{displaystyle a(x,t)=left({frac {partial }{partial t}}+{frac {1}{2}}{frac {partial ^{2}}{partial x^{2}}}right)p(x,t).}

Ejemplo: ${displaystyle p(x,t)=left(x^{2}-tright)^{2},}$ $a(x,t)=4x^{2};$ el proceso

{displaystyle left(W_{t}^{2}-tright)^{2}-4int _{0}^{t}W_{s}^{2},mathrm {d} s}

W_{t}^{2}-t

{displaystyle 4int _{0}^{t}W_{s}^{2},mathrm {d} s.}

Acerca de las funciones $p (xa, t)$ más generales que los polinomios, consulte martingalas locales.

Algunas propiedades de las rutas de muestra

El conjunto de todas las funciones w con estas propiedades es de medida Wiener completa. Es decir, un camino (función de muestra) del proceso de Wiener tiene casi con seguridad todas estas propiedades.

Propiedades cualitativas

Para cada ε > 0, la función w toma ambos valores (strictamente) positivos y (strictamente) negativos en (0, ε).
La función w es continua en todas partes pero diferenciable en ninguna parte (como la función Weierstrass).
Puntos de máximo local de la función w son un conjunto denso contable; los valores máximos son iguales; cada máximo local es agudo en el siguiente sentido: si w tiene un máximo local $t$ entonces ${displaystyle lim _{sto t}{frac {|w(s)-w(t)|}{|s-t|}}to infty.}$ Lo mismo ocurre con la minima local.
La función w no tiene puntos de aumento local, es decir, no t 0 satisfice lo siguiente para algunos ε en (0, t): primero, w()s≤ w()t) para todos s ent − ε, t), y segundo, w()s) ≥ w()t) para todos s ent, t + ε). (El aumento local es una condición más débil que esa w está aumentando en (t − ε, t + ε). Lo mismo ocurre con la disminución local.
La función w es de variación sin límites en cada intervalo.
La variación cuadrática de w [0,t] es t.
Cero de la función w son un conjunto denso perfecto de la medida Lebesgue 0 y la dimensión Hausdorff 1/2 (antes, incontable).

Propiedades cuantitativas

Ley del logaritmo iterado

{displaystyle limsup _{tto +infty }{frac {|w(t)|}{sqrt {2tlog log t}}}=1,quad {text{almost surely}}.}

Módulo de continuidad

Módulo local de continuidad:

{displaystyle limsup _{varepsilon to 0+}{frac {|w(varepsilon)|}{sqrt {2varepsilon log log(1/varepsilon)}}}=1,qquad {text{almost surely}}.}

Módulo de continuidad global (Lévy):

<math alttext="{displaystyle limsup _{varepsilon to 0+}sup _{0leq slim supε ε → → 0+Sup0≤ ≤ s.t≤ ≤ 1,t− − s≤ ≤ ε ε Silenciow()s)− − w()t)Silencio2ε ε log⁡ ⁡ ()1/ε ε )=1,casi seguro.{displaystyle limsup _{varepsilon to 0+}sup _{0leq s wontleq 1,t-sleq varepsilon }{frac { perpetuaw(s)-w(t) quiet}{sqrt {2varepsilon log(1/varepsilon)} {} {}{} {} {} {}}}}}}}}}}}} {} {}}}}}}}}}}}}} {qquad} {}}}}}}}}} {<img alt="{displaystyle limsup _{varepsilon to 0+}sup _{0leq s

Teorema de duplicación de dimensiones

Los teoremas de duplicación de dimensiones dicen que la dimensión de Hausdorff de un conjunto bajo un movimiento browniano se duplica casi con seguridad.

Hora local

La imagen de la medida de Lebesgue en [0, t] debajo del mapa w (la medida de avance) tiene una densidad $L t$ . De este modo,

{displaystyle int _{0}^{t}f(w(s)),mathrm {d} s=int _{-infty }^{+infty }f(x)L_{t}(x),mathrm {d} x}

fL_tL_txxwtxababwtxxttxw

Estas propiedades de continuidad no son triviales. Considere que la hora local también se puede definir (como la densidad de la medida de avance) para una función suave. Entonces, sin embargo, la densidad es discontinua, a menos que la función dada sea monótona. En otras palabras, existe un conflicto entre el buen comportamiento de una función y el buen comportamiento de su hora local. En este sentido, la continuidad del tiempo local del proceso de Wiener es otra manifestación de la falta de suavidad de la trayectoria.

Tasa de información

La tasa de información del proceso de Wiener con respecto a la distancia de error al cuadrado, es decir, su función de distorsión de tasa cuadrática, viene dada por

{displaystyle R(D)={frac {2}{pi ^{2}ln 2D}}approx 0.29D^{-1}.}

{displaystyle {w_{t}}_{tin [0,T]}}

{displaystyle TR(D)}

D

0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle varepsilon }0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e04ec3670b50384a3ce48aca42e7cc5131a06b12" style="vertical-align: -0.338ex; width:5.344ex; height:2.176ex;"/>

T

{displaystyle 2^{TR(D)}}

{displaystyle {w_{t}}_{tin [0,T]}}

{displaystyle D-varepsilon }

En muchos casos, es imposible codificar el proceso de Wiener sin mostrarlo primero. Cuando el proceso de Wiener se muestra a intervalos $T_{s}$ antes de aplicar un código binario para representar estas muestras, el comercio óptimo entre la tasa de código ${displaystyle R(T_{s},D)}$ y esperado error cuadrado $D$ (en la estimación del proceso continuo de Wiener) sigue la representación paramétrica

{displaystyle R(T_{s},D_{theta })={frac {T_{s}}{2}}int _{0}^{1}log _{2}^{+}left[{frac {S(varphi)-{frac {1}{6}}}{theta }}right]dvarphi}

{displaystyle D_{theta }={frac {T_{s}}{6}}+T_{s}int _{0}^{1}min left{S(varphi)-{frac {1}{6}},theta right}dvarphi}

{displaystyle S(varphi)=(2sin(pi varphi /2))^{-2}}

{displaystyle log ^{+}[x]=max{0,log(x)}}

{displaystyle T_{s}/6}

Procesos relacionados

Procesos de Wiener con derivaazul) y sin deriva (rojo).

2D Procesos de Wiener con derivaazul) y sin deriva (rojo).

El generador de un movimiento Browniano es 1.2 veces el operador de Laplace-Beltrami. La imagen anterior es del movimiento marroniano sobre un conjunto especial: la superficie de una esfera.

El proceso estocástico definido por

{displaystyle X_{t}=mu t+sigma W_{t}}

Proceso de Wiener con deriva μ²

A grandes rasgos, aparecen dos procesos aleatorios en el intervalo de tiempo [0, 1] cuando se condiciona el proceso de Wiener para que desaparezca en ambos extremos de [0,1]. Sin más condicionamiento, el proceso toma valores tanto positivos como negativos en [0, 1] y se denomina puente browniano. Condicionado también a permanecer positivo en (0, 1), el proceso se llama excursión browniana. En ambos casos un tratamiento riguroso implica un procedimiento limitante, ya que la fórmula P(A|B) = P (A ∩ B)/P(B) no se aplica cuando P (B) = 0.

Se puede escribir un movimiento browniano geométrico

{displaystyle e^{mu t-{frac {sigma ^{2}t}{2}}+sigma W_{t}}.}

Es un proceso estocástico que se utiliza para modelar procesos que nunca pueden tomar valores negativos, como el valor de las acciones.

El proceso estocástico

{displaystyle X_{t}=e^{-t}W_{e^{2t}}}

{displaystyle theta =1}

mu =0

{displaystyle sigma ^{2}=2}

El tiempo de golpear un solo punto x > 0 por el proceso de Wiener es una variable aleatoria con la distribución de Lévy. La familia de estas variables aleatorias (indexadas por todos los números positivos x) es una modificación continua por la izquierda de un proceso de Lévy. La modificación continua por la derecha de este proceso viene dada por los tiempos de la primera salida de los intervalos cerrados [0, x].

La hora local $L = (L x t) x \in R, t \geq 0$ de un movimiento browniano describe el tiempo que el proceso pasa en el punto x. Formalmente

{displaystyle L^{x}(t)=int _{0}^{t}delta (x-B_{t}),ds}

Martingalas brownianas

Sea A un evento relacionado con el proceso de Wiener (más formalmente: un conjunto, medible con respecto a la medida de Wiener, en el espacio de funciones), y X_t la probabilidad condicional de A dado el proceso de Wiener en el intervalo de tiempo [0, t] (más formalmente: la medida de Wiener de la conjunto de trayectorias cuya concatenación con la trayectoria parcial dada en [0, t] pertenece a A). Entonces el proceso X_t es una martingala continua. Su propiedad de martingala se sigue inmediatamente de las definiciones, pero su continuidad es un hecho muy especial, un caso especial de un teorema general que establece que todas las martingalas brownianas son continuas. Una martingala browniana es, por definición, una martingala adaptada a la filtración browniana; y la filtración browniana es, por definición, la filtración generada por el proceso de Wiener.

Movimiento browniano integrado

La integral temporal del proceso de Wiener

{displaystyle W^{(-1)}(t):=int _{0}^{t}W(s),ds}

movimiento Browniano integradoproceso integrado de WienerNt³

{displaystyle twedge s=min(t,s)}

Para el caso general del proceso definido por

{displaystyle V_{f}(t)=int _{0}^{t}f'(s)W(s),ds=int _{0}^{t}(f(t)-f(s)),dW_{s}}

0}" xmlns="http://www.w3.org/1998/Math/MathML">a■0{displaystyle a confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1f34a80ea013edb56e340b19550430a8b6dfd7b9" style="vertical-align: -0.338ex; width:5.491ex; height:2.176ex;"/>

{displaystyle operatorname {Var} (V_{f}(t))=int _{0}^{t}(f(t)-f(s))^{2},ds}

{displaystyle operatorname {cov} (V_{f}(t+a),V_{f}(t))=int _{0}^{t}(f(t+a)-f(s))(f(t)-f(s)),ds}

{displaystyle V_{f}(t)}

{displaystyle V_{f}(t+a)}

{displaystyle V_{f}(t)}

{displaystyle V_{f}(t+a)=Acdot V_{f}(t)+Bcdot Z}

{displaystyle A={frac {operatorname {cov} (V_{f}(t+a),V_{f}(t))}{operatorname {Var} (V_{f}(t))}}}

{displaystyle B^{2}=operatorname {Var} (V_{f}(t+a))-A^{2}operatorname {Var} (V_{f}(t))}

{displaystyle V_{f}(t)=W^{(-1)}(t)}

{displaystyle f(t)=t}

{displaystyle {frac {t}{2n+1}}left({frac {t^{n}}{n!}}right)^{2}}

Cambio de hora

Cada martingala continua (comenzando en el origen) es un proceso de Wiener con cambio de tiempo.

Ejemplo: 2W_t = V(4 t) donde V es otro proceso de Wiener (diferente de W pero distribuido como W).

Ejemplo. $W_{t}^{2}-t=V_{A(t)}$ Donde $A(t)=4int _{0}^{t}W_{s}^{2},mathrm {d} s$ y V es otro proceso de Wiener.

En general, si M es un martingale continuo entonces $M_{t}-M_{0}=V_{A(t)}$ Donde A()t) es la variación cuadrática de M [0, t], y V es un proceso de Wiener.

Corolario. (Véase también los teoremas de convergencia de la martingala de Doob) Sea M_t una martingala continua, y

{displaystyle M_{infty }^{-}=liminf _{tto infty }M_{t},}

{displaystyle M_{infty }^{+}=limsup _{tto infty }M_{t}.}

Entonces solo son posibles los siguientes dos casos:

<math alttext="{displaystyle -infty <M_{infty }^{-}=M_{infty }^{+}− − JUEGO JUEGO .MJUEGO JUEGO − − =MJUEGO JUEGO +.+JUEGO JUEGO ,{displaystyle - Bien.<img alt="{displaystyle -infty <M_{infty }^{-}=M_{infty }^{+}

<math alttext="{displaystyle -infty =M_{infty }^{-}− − JUEGO JUEGO =MJUEGO JUEGO − − .MJUEGO JUEGO +=+JUEGO JUEGO ;{displaystyle - Bien.<img alt="{displaystyle -infty =M_{infty }^{-}

M_{infty }^{-}=M_{infty }^{+}=+infty

<math alttext="{displaystyle M_{infty }^{-}<M_{infty }^{+}MJUEGO JUEGO − − .MJUEGO JUEGO +.+JUEGO JUEGO {displaystyle M_{infty } {cHFF} {infty } {c} {cc} {ccH00}<img alt="M_{infty }^{-}<M_{infty }^{+}

Especialmente, una martingala continua no negativa tiene un límite finito (como t → ∞) casi seguro.

Todo lo establecido (en esta subsección) para las martingalas también se aplica a las martingalas locales.

Cambio de medida

Una amplia clase de semimartingalas continuas (especialmente, de procesos de difusión) está relacionada con el proceso de Wiener a través de una combinación de cambio de tiempo y cambio de medida.

Usando este hecho, las propiedades cualitativas establecidas anteriormente para el proceso de Wiener se pueden generalizar a una amplia clase de semimartingalas continuas.

Proceso de Wiener de valor complejo

El proceso de Wiener de valor complejo puede definirse como un proceso aleatorio de valor complejo de la forma ${displaystyle Z_{t}=X_{t}+iY_{t}}$ Donde $X_{t}$ y $Y_{t}$ son procesos independientes de Wiener (valor real).

Autosimilitud

Escala browniana, inversión de tiempo, inversión de tiempo: lo mismo que en el caso de valor real.

Invariancia de rotación: para cada número complejo $c$ tales que ${displaystyle |c|=1}$ el proceso ${displaystyle ccdot Z_{t}}$ es otro proceso de Wiener de valor complejo.

Cambio de hora

Si $f$ es una función entera entonces el proceso ${displaystyle f(Z_{t})-f(0)}$ es un proceso de Wiener de valor complejo cambiado de tiempo.

Ejemplo: ${displaystyle Z_{t}^{2}=left(X_{t}^{2}-Y_{t}^{2}right)+2X_{t}Y_{t}i=U_{A(t)}}$ Donde

{displaystyle A(t)=4int _{0}^{t}|Z_{s}|^{2},mathrm {d} s}

U

En contraste con el caso real, un martingale de valor complejo generalmente no es un proceso de Wiener de valor complejo cambiado de tiempo. Por ejemplo, el martingale ${displaystyle 2X_{t}+iY_{t}}$ no es (aquí $X_{t}$ y $Y_{t}$ son procesos independientes Wiener, como antes).

Contenido relacionado

Más resultados...

Proceso de salchicha

Caracterizaciones del proceso Wiener

Proceso de Wiener como límite de paseo aleatorio

Propiedades de un proceso de Wiener unidimensional

Propiedades básicas

Covarianza y correlación

Representación de Viena

Máxima corriente

Autosimilitud

Escala browniana

Reversión del tiempo

Inversión de tiempo

Una clase de martingalas brownianas

Algunas propiedades de las rutas de muestra

Propiedades cualitativas

Propiedades cuantitativas

Ley del logaritmo iterado

Módulo de continuidad

Teorema de duplicación de dimensiones

Hora local

Tasa de información

Procesos relacionados

Martingalas brownianas

Movimiento browniano integrado

Cambio de hora

Cambio de medida

Proceso de Wiener de valor complejo

Autosimilitud

Cambio de hora

Contenido relacionado

Marco de referencia

Función de probabilidad

Fred cantante