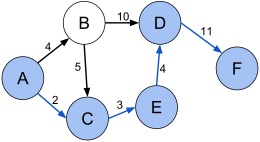
Problema del camino más corto

Camino más corto (A, C, E, D, F) entre los vértices A y F en el gráfico dirigido ponderado

En teoría de grafos, el problema del camino más corto es el problema de encontrar un camino entre dos vértices (o nodos) en un gráfico tal que la suma de los pesos de sus aristas constituyentes se minimice.

El problema de encontrar la ruta más corta entre dos intersecciones en un mapa de carreteras puede modelarse como un caso especial del problema de la ruta más corta en gráficos, donde los vértices corresponden a intersecciones y los bordes corresponden a segmentos de carretera, cada uno ponderado por el longitud del segmento.

Definición

El problema de la ruta más corta se puede definir para grafos, ya sean no dirigidos, dirigidos o mixtos. Se define aquí para grafos no dirigidos; para grafos dirigidos la definición de camino requiere que los vértices consecutivos estén conectados por un borde dirigido apropiado.

Dos vértices están adyacentes cuando ambos son incidentes a un borde común. Un camino en un gráfico no dirigido es una secuencia de vértices ${displaystyle P=(v_{1},v_{2},ldotsv_{n})in Vtimes Vtimes cdots times V}$tales que ${displaystyle V_{i}$ está adyacente ${displaystyle v_{i+1}$ para ${displaystyle 1leq I didn't}$. Tal camino ${displaystyle P}$ se llama un camino de longitud ${displaystyle n-1}$desde ${displaystyle v_{1}$ a ${displaystyle V_{n}$. (El ${displaystyle V_{i}$ son variables; su numeración aquí se relaciona con su posición en la secuencia y necesita no relacionarse con cualquier etiquetado canónico de los vértices.)

Vamos ${displaystyle e_{i,j}$ ser el incidente del borde a ambos ${displaystyle V_{i}$ y ${displaystyle v_{j}$. Dada una función de peso real ${displaystyle f:Erightarrow {R}$, y un gráfico no dirigido (simple) ${displaystyle G.$, el camino más corto de ${displaystyle v}$ a ${displaystyle v'}$ es el camino ${displaystyle P=(v_{1},v_{2},ldotsv_{n}}$ (donde) ${displaystyle v_{1}=v}$ y ${displaystyle v_{n}=v}$) que sobre todo posible ${displaystyle n}$ minimiza la suma ${displaystyle sum _{i=1}^{n-1}f(e_{i,i+1}). }$ Cuando cada borde en el gráfico tiene peso unitario o ${displaystyle f:Erightarrow {1}}$, esto es equivalente a encontrar el camino con pocos bordes.

El problema también se denomina a veces problema de la ruta más corta de un solo par, para distinguirlo de las siguientes variaciones:

• El problema de ruta más corto de un solo fuente, en el que tenemos que encontrar caminos más cortos de un vertex fuente v a todos los otros vértices del gráfico.
• El problema de ruta más corto de la destinación, en el que tenemos que encontrar caminos más cortos de todos los vértices en el gráfico dirigido a un solo destino vertex v. Esto se puede reducir al problema de la ruta más corta de un solo recurso revirtiendo los arcos en el gráfico dirigido.
• El all-pairs más corto problema de ruta, en el que tenemos que encontrar caminos más cortos entre cada par de vértices v, v ' en el gráfico.

Estas generalizaciones tienen algoritmos significativamente más eficientes que el enfoque simplista de ejecutar un algoritmo de ruta más corta de un solo par en todos los pares de vértices relevantes.

Algoritmos

Los algoritmos más importantes para resolver este problema son:

• El algoritmo de Dijkstra resuelve el problema de ruta más corto de una sola fuente con peso de borde no negativo.
• El algoritmo Bellman-Ford resuelve el problema de una sola fuente si los pesos del borde pueden ser negativos.
• Un algoritmo de búsqueda* resuelve el camino más corto de un solo pago utilizando heurísticas para intentar acelerar la búsqueda.
• El algoritmo Floyd–Warshall resuelve todos los pares de caminos más cortos.
• El algoritmo de Johnson resuelve todos los pares de caminos más cortos, y puede ser más rápido que Floyd–Warshall en gráficos escasos.
• El algoritmo de Viterbi resuelve el problema más corto de la ruta estocástica con un peso probabilístico adicional en cada nodo.

Se pueden encontrar algoritmos adicionales y evaluaciones asociadas en Cherkassky, Goldberg & Radzik (1996).

Rutas más cortas de fuente única

Gráficos no dirigidos

Pesos	Complejo de tiempo	Autor
${displaystyle mathbb {R}$+	O()V2)	Dijkstra 1959
${displaystyle mathbb {R}$+	O()E+V) logV)	Johnson 1977
${displaystyle mathbb {R}$+	O()E+VlogV)	Fredman " Tarjan 1984 (Jabón de Fibonacci)
${displaystyle mathbb {N}$	O()E)	Thorup 1999 (requiere multiplicación de tiempo constante)

Gráficos no ponderados

Gráficos acíclicos dirigidos (DAG)

Un algoritmo que utiliza clasificación topológica puede resolver el problema de la ruta más corta de fuente única en el tiempo Θ(E + V) en DAG arbitrariamente ponderados.

Gráficos dirigidos con pesos no negativos

La siguiente tabla está tomada de Schrijver (2004), con algunas correcciones y adiciones. Un fondo verde indica un mejor límite asintóticamente en la tabla; L es la longitud máxima (o peso) entre todos los bordes, suponiendo pesos de borde enteros.

Pesos	Algoritm	Complejo de tiempo	Autor
${displaystyle mathbb {R}$		${displaystyle O(V^{2}EL)}$	Ford 1956
${displaystyle mathbb {R}$	Algoritmo de Bellman-Ford	${displaystyle O(VE)}$	Shimbel 1955, Bellman 1958, Moore 1959
${displaystyle mathbb {R}$		${displaystyle O(V^{2}log {V}}$	Dantzig 1960
${displaystyle mathbb {R}$	algoritmo de Dijkstra con lista	${displaystyle O(V^{2}}$	Leyzorek et al. 1957, Dijkstra 1959, Minty (véase Pollack & Wiebenson 1960), Whiting & Hillier 1960
${displaystyle mathbb {R}$	algoritmo de Dijkstra con montón binario	${displaystyle O(E+V)log {V}$	Johnson 1977
${displaystyle mathbb {R}$	El algoritmo de Dijkstra con el montón de Fibonacci	${displaystyle O(E+Vlog {V})}$	Fredman " Tarjan 1984, Fredman " Tarjan 1987
${displaystyle mathbb {N}$	algoritmo de Dial (algoritmo de Dijkstra usando una cola de cubo con L cubos)	${displaystyle O(E+LV)}$	Dial 1969
		${displaystyle O(Elog {log {})}$	Johnson 1981, Karlsson " Poblete 1983
	El algoritmo de Gabow	${displaystyle O(Elog _{E/V}L)}$	Gabow 1983, Gabow 1985
		${displaystyle O(E+V{sqrt {log {L}}}}}$	Ahuja et al. 1990
	Thorup	${displaystyle O(E+Vlog {log {V}}}$	Thorup 2004

Gráficos dirigidos con pesos arbitrarios sin ciclos negativos

Pesos	Algoritm	Complejo de tiempo	Autor
${displaystyle mathbb {R}$		O()V 2EL)	Ford 1956
${displaystyle mathbb {R}$	Algoritmo de Bellman-Ford	O()VE)	Shimbel 1955, Bellman 1958, Moore 1959
${displaystyle mathbb {R}$	Johnson-Dijkstra con montón binario	O()V()E+ registroV)	Johnson 1977
${displaystyle mathbb {R}$	Johnson-Dijkstra con el montón de Fibonacci	O()V()E+ registroV)	Fredman " Tarjan 1984, Fredman " Tarjan 1987, adaptado después de Johnson 1977
${displaystyle mathbb {N}$	Técnica de Johnson aplicada al algoritmo de Dial	O()V()E+L)	Diario 1969, adaptado después de Johnson 1977

Gráficos dirigidos con pesos arbitrarios con ciclos negativos

Encuentra un ciclo negativo o calcula las distancias a todos los vértices.

Pesos	Algoritm	Complejo de tiempo	Autor
${displaystyle mathbb {Z}$	Andrew V. Goldberg	${displaystyle O(E{sqrt {}log {N}}}$

Gráficos planos con pesos no negativos

Pesos	Algoritm	Complejo de tiempo	Autor
${displaystyle mathbb {R} _{geq #$		${displaystyle O(V)}$	Henzinger et al. 1997

Rutas más cortas de todos los pares

El problema del camino más corto de todos los pares encuentra los caminos más cortos entre cada par de vértices v, v' en el gráfico. Shimbel (1953) introdujo el problema de los caminos más cortos de todos los pares para gráficos dirigidos no ponderados, quien observó que podía resolverse mediante un número lineal de multiplicaciones de matrices que toma un tiempo total de O(V⁴).

Gráfica no dirigida

Pesos	Complejo de tiempo	Algoritm
${displaystyle mathbb {R}$+	O()V3)	Floyd–Warshall algoritmo
${displaystyle {1,infty}$	${displaystyle O(V^{omega }log V)}$	algoritmo de Seidel (tiempo de funcionamiento previsto)
${displaystyle mathbb {N}$	${displaystyle O(V^{3}/2}{\ Omega.$	Williams 2014
${displaystyle mathbb {R}$+	O()EVlog α(E,V)	Pettie " Ramachandran 2002
${displaystyle mathbb {N}$	O()EV)	Thorup 1999 aplicado a cada vértice (requiere multiplicación de tiempo constante).

Gráfico dirigido

Pesos	Complejo de tiempo	Algoritm
${displaystyle mathbb {R}$ (sin ciclos negativos)	O()V3)	Floyd–Warshall algoritmo
${displaystyle mathbb {N}$	${displaystyle O(V^{3}/2}{\ Omega.$	Williams 2014
${displaystyle mathbb {R}$ (sin ciclos negativos)	O()EV+V2logV)	Johnson-Dijkstra
${displaystyle mathbb {R}$ (sin ciclos negativos)	O()EV+V2logV)	Pettie 2004
${displaystyle mathbb {N}$	O()EV+V2logV)	Hagerup 2000

Aplicaciones

Los algoritmos de ruta más corta se aplican para encontrar automáticamente direcciones entre ubicaciones físicas, como direcciones de manejo en sitios web de mapas web como MapQuest o Google Maps. Para esta aplicación se dispone de algoritmos especializados rápidos.

Si uno representa una máquina abstracta no determinista como un gráfico donde los vértices describen estados y los bordes describen posibles transiciones, los algoritmos de ruta más corta se pueden usar para encontrar una secuencia óptima de opciones para alcanzar un determinado estado objetivo, o para establecer límites inferiores en el tiempo necesario para alcanzar un estado dado. Por ejemplo, si los vértices representan los estados de un rompecabezas como un cubo de Rubik y cada borde dirigido corresponde a un solo movimiento o giro, se pueden usar algoritmos de ruta más corta para encontrar una solución que use el mínimo número posible de movimientos.

En una mentalidad de redes o telecomunicaciones, este problema de la ruta más corta a veces se denomina problema de la ruta de retraso mínimo y, por lo general, se relaciona con un problema de la ruta más ancha. Por ejemplo, el algoritmo puede buscar el camino más corto (retraso mínimo) más ancho, o el camino más corto (retraso mínimo) más ancho.

Una aplicación más alegre son los juegos de "seis grados de separación" que tratan de encontrar el camino más corto en gráficos como estrellas de cine que aparecen en la misma película.

Otras aplicaciones, a menudo estudiadas en la investigación de operaciones, incluyen diseño de plantas e instalaciones, robótica, transporte y diseño VLSI.

Redes de carreteras

Una red de carreteras se puede considerar como un gráfico con pesos positivos. Los nodos representan cruces de carreteras y cada borde del gráfico está asociado con un segmento de carretera entre dos cruces. El peso de un borde puede corresponder a la longitud del segmento de carretera asociado, el tiempo necesario para atravesar el segmento o el costo de atravesar el segmento. Usando bordes dirigidos también es posible modelar calles de un solo sentido. Dichos gráficos son especiales en el sentido de que algunos bordes son más importantes que otros para viajes de larga distancia (por ejemplo, autopistas). Esta propiedad se ha formalizado utilizando la noción de dimensión vial. Hay una gran cantidad de algoritmos que explotan esta propiedad y, por lo tanto, pueden calcular la ruta más corta mucho más rápido de lo que sería posible en gráficos generales.

Todos estos algoritmos funcionan en dos fases. En la primera fase, el gráfico se preprocesa sin conocer el nodo de origen o de destino. La segunda fase es la fase de consulta. En esta fase, se conocen los nodos de origen y de destino. La idea es que la red de carreteras sea estática, por lo que la fase de preprocesamiento se puede hacer una sola vez y utilizar para una gran cantidad de consultas en la misma red de carreteras.

El algoritmo con el tiempo de consulta más rápido conocido se denomina etiquetado central y puede calcular la ruta más corta en las redes de carreteras de Europa o EE. UU. en una fracción de microsegundo. Otras técnicas que se han utilizado son:

• ALT (A* búsqueda, hitos y desigualdad triangular)
• Banderas de arco
• Jerarquías de tracción
• Nodo de tránsito routing
• Corridas basadas en el alcance
• Etiqueta
• Etiquetas de Hub

En 2011, Glasgow tenía 53 470 estudiantes de tiempo completo de entre 18 y 74 años que residían en la ciudad durante el período lectivo, más que cualquier otra ciudad de Escocia y la quinta cifra más alta del Reino Unido fuera de Londres. La mayoría de los que viven fuera de casa residen en Shawlands, Dennistoun y el West End de la ciudad.

El Ayuntamiento gestiona 29 escuelas secundarias, 149 escuelas primarias y tres escuelas especializadas: Dance School of Scotland, Glasgow School of Sport y Glasgow Gaelic School (Sgoil Ghàidhlig Ghlaschu), la única escuela secundaria escuela en Escocia para enseñar exclusivamente en gaélico. Las instalaciones de educación al aire libre son proporcionadas por el ayuntamiento en el Centro Blairvadach, cerca de Helensburgh. Jordanhill School es operada directamente por el gobierno escocés. Glasgow también tiene varias escuelas independientes, incluida The High School of Glasgow, fundada en 1124 y la escuela más antigua de Escocia; Hutchesons' Grammar School, fundada en 1639 y una de las instituciones escolares más antiguas de Gran Bretaña; y otros como Craigholme School (cerrado en 2020), Glasgow Academy, Kelvinside Academy y St. Aloysius' Facultad. Glasgow es parte de la Red Global de Ciudades del Aprendizaje de la UNESCO.

Deporte

Fútbol

Rutas con restricciones

A diferencia del problema de la ruta más corta, que se puede resolver en tiempo polinomial en gráficos sin ciclos negativos, los problemas de la ruta más corta que incluyen restricciones adicionales en la ruta de solución deseada se denominan Primero la ruta más corta restringida y son más difíciles de resolver. Un ejemplo es el problema de la ruta más corta restringida, que intenta minimizar el costo total de la ruta y, al mismo tiempo, mantiene otra métrica por debajo de un umbral determinado. Esto hace que el problema sea NP-completo (no se cree que estos problemas se puedan resolver de manera eficiente para grandes conjuntos de datos, consulte el problema P = NP). Otro ejemplo de NP-completo requiere que se incluya un conjunto específico de vértices en la ruta, lo que hace que el problema sea similar al Problema del viajante de comercio (TSP). El TSP es el problema de encontrar el camino más corto que pase por cada vértice exactamente una vez y regrese al principio. El problema de encontrar el camino más largo en un gráfico también es NP-completo.

Observabilidad parcial

El problema del viajero canadiense y el problema del camino más corto estocástico son generalizaciones donde el gráfico no es completamente conocido por el motor, cambia con el tiempo o donde las acciones (recorridos) son probabilísticas.

Rutas estratégicas más cortas

A veces, los bordes de un gráfico tienen personalidades: cada borde tiene su propio interés egoísta. Un ejemplo es una red de comunicación, en la que cada borde es una computadora que posiblemente pertenece a una persona diferente. Diferentes computadoras tienen diferentes velocidades de transmisión, por lo que cada borde de la red tiene un peso numérico igual a la cantidad de milisegundos que se tarda en transmitir un mensaje. Nuestro objetivo es enviar un mensaje entre dos puntos de la red en el menor tiempo posible. Si conocemos el tiempo de transmisión de cada computadora (el peso de cada borde), entonces podemos usar un algoritmo estándar de caminos más cortos. Si no conocemos los tiempos de transmisión, entonces tenemos que pedirle a cada computadora que nos diga su tiempo de transmisión. Pero, las computadoras pueden ser egoístas: una computadora puede decirnos que su tiempo de transmisión es muy largo, para que no la molestemos con nuestros mensajes. Una posible solución a este problema es utilizar una variante del mecanismo VCG, que da a las computadoras un incentivo para revelar sus verdaderos pesos.

Detección de ciclos negativos

En algunos casos, el objetivo principal no es encontrar el camino más corto, sino solo detectar si el gráfico contiene un ciclo negativo. Se pueden usar algunos algoritmos de rutas más cortas para este propósito:

• El algoritmo Bellman-Ford se puede utilizar para detectar un ciclo negativo en el tiempo ${displaystyle O(viviendas)$.
• Cherkassky y Goldberg encuestan varios otros algoritmos para la detección del ciclo negativo.

Marco algebraico general sobre semianillos: el problema del camino algebraico

Muchos problemas se pueden enmarcar como una forma de camino más corto para algunas nociones de suma adecuadamente sustituidas a lo largo de un camino y tomando el mínimo. El enfoque general para estos es considerar las dos operaciones como las de un semiring. La multiplicación de Semiring se realiza a lo largo del camino, y la suma se realiza entre caminos. Este marco general se conoce como el problema del camino algebraico.

La mayoría de los algoritmos clásicos de ruta más corta (y los nuevos) se pueden formular para resolver sistemas lineales sobre tales estructuras algebraicas.

Más recientemente, se ha desarrollado un marco aún más general para resolver estos (y problemas mucho menos relacionados) bajo el lema de álgebras de valoración.

Ruta más corta en redes estocásticas dependientes del tiempo

En situaciones de la vida real, la red de transporte suele ser estocástica y dependiente del tiempo. De hecho, un viajero que atraviesa un enlace diariamente puede experimentar diferentes tiempos de viaje en ese enlace debido no solo a las fluctuaciones en la demanda de viajes (matriz origen-destino) sino también a incidentes tales como zonas de trabajo, malas condiciones climáticas, accidentes y averías de vehículos.. Como resultado, una red estocástica dependiente del tiempo (STD) es una representación más realista de una red de carreteras real en comparación con la determinista.

A pesar de un progreso considerable durante el transcurso de la última década, sigue siendo una cuestión controvertida cómo se debe definir e identificar una ruta óptima en las redes de carreteras estocásticas. En otras palabras, no existe una definición única de un camino óptimo bajo incertidumbre. Una respuesta posible y común a esta pregunta es encontrar un camino con el tiempo de viaje mínimo esperado. La principal ventaja de usar este enfoque es que los algoritmos de ruta más corta eficientes introducidos para las redes deterministas se pueden emplear fácilmente para identificar la ruta con el tiempo de viaje mínimo esperado en una red estocástica. Sin embargo, la ruta óptima resultante identificada por este enfoque puede no ser confiable, porque este enfoque no aborda la variabilidad del tiempo de viaje. Para abordar este problema, algunos investigadores utilizan la distribución del tiempo de viaje en lugar del valor esperado del mismo, por lo que encuentran la distribución de probabilidad del tiempo total de viaje utilizando diferentes métodos de optimización, como la programación dinámica y el algoritmo de Dijkstra. Estos métodos utilizan optimización estocástica, específicamente programación dinámica estocástica para encontrar el camino más corto en redes con longitud de arco probabilística. El concepto de confiabilidad del tiempo de viaje se usa indistintamente con la variabilidad del tiempo de viaje en la literatura de investigación del transporte, por lo que, en general, se puede decir que cuanto mayor sea la variabilidad en el tiempo de viaje, menor será la confiabilidad y viceversa.

Para dar cuenta de la confiabilidad del tiempo de viaje con mayor precisión, se han sugerido dos definiciones alternativas comunes para una ruta óptima bajo incertidumbre. Algunos han introducido el concepto de la ruta más confiable, con el objetivo de maximizar la probabilidad de llegar a tiempo o antes de un presupuesto de tiempo de viaje determinado. Otros, alternativamente, han presentado el concepto de una ruta α-confiable basada en la cual intentaron minimizar el presupuesto de tiempo de viaje requerido para asegurar una probabilidad de llegada a tiempo especificada previamente.