Problema de secretaria

El problema de la secretaria demuestra un escenario que involucra la teoría de detención óptima que se estudia ampliamente en los campos de la probabilidad aplicada, la estadística y la teoría de la decisión. También se le conoce como el problema del matrimonio, el problema de la dote del sultán, el problema del pretendiente quisquilloso, el juego del googol. y el problema de la mejor elección. Su solución también se conoce como la regla del 37%.

La forma básica del problema es la siguiente: imagine un administrador que quiere contratar al mejor secretario fuera de ${\displaystyle n}$ Solicitantes clasificables para un puesto. Los solicitantes son entrevistados uno por uno en orden aleatorio. Una decisión sobre cada solicitante en particular debe tomarse inmediatamente después de la entrevista. Una vez rechazado, un solicitante no puede ser recordado. Durante la entrevista, el administrador obtiene información suficiente para clasificar al solicitante entre todos los solicitantes entrevistados hasta ahora, pero no tiene conocimiento de la calidad de los solicitantes aún no vistos. La pregunta es sobre la estrategia óptima (regla de selección) para maximizar la probabilidad de seleccionar al mejor solicitante. Si la decisión puede aplazarse hasta el final, esto puede ser resuelto por el simple algoritmo de selección máxima de seguimiento del máximo de funcionamiento (y quién lo logró), y seleccionando el máximo global al final. La dificultad es que la decisión debe tomarse inmediatamente.

La prueba rigurosa más corta conocida hasta ahora es proporcionada por el algoritmo de probabilidades. Implica que la probabilidad de ganar óptima sea siempre al menos ${\displaystyle 1/e}$ (donde) e es la base del logaritmo natural), y que este último sostiene incluso en una generalidad mucho mayor. La regla de parada óptima prescribe siempre rechazar la primera ${\displaystyle \sim n/e}$ solicitantes que son entrevistados y luego se detienen en el primer solicitante que es mejor que cada solicitante entrevistado hasta ahora (o continuando con el último solicitante si esto nunca ocurre). A veces esta estrategia se llama ${\displaystyle 1/e}$ parar la regla, porque la probabilidad de parar en el mejor solicitante con esta estrategia ya se trata de ${\displaystyle 1/e}$ para valores moderados ${\displaystyle n}$. Una razón por la que el problema del secretario ha recibido tanta atención es que la política óptima para el problema (la regla de parada) es simple y selecciona al mejor candidato alrededor del 37% del tiempo, independientemente de si hay 100 o 100 millones de solicitantes.

Formulación

Aunque existen muchas variaciones, el problema básico se puede plantear de la siguiente manera:

• Hay una sola posición para llenar.
• Hay n solicitantes para la posición, y el valor de n es conocido.
• Los solicitantes, si todos se ven juntos, pueden clasificarse de lo mejor a lo peor sin ambigüedad.
• Los solicitantes son entrevistados secuencialmente en orden aleatorio, y cada orden es igualmente probable.
• Inmediatamente después de una entrevista, el solicitante entrevistado es aceptado o rechazado, y la decisión es irrevocable.
• La decisión de aceptar o rechazar a un solicitante sólo puede basarse en las filas relativas de los solicitantes entrevistados hasta ahora.
• El objetivo de la solución general es tener la mayor probabilidad de seleccionar al mejor solicitante de todo el grupo. Esto es lo mismo que maximizar el pago esperado, con payoff definido como uno para el mejor solicitante y cero de otro modo.

Un candidato se define como un solicitante que, cuando es entrevistado, es mejor que todos los solicitantes entrevistados anteriormente. Saltar se utiliza para significar "rechazar inmediatamente después de la entrevista". Dado que el objetivo del problema es seleccionar al mejor solicitante, solo se considerarán los candidatos para su aceptación. El "candidato" en este contexto corresponde al concepto de registro en permutación.

Obtener la política óptima

La política óptima para el problema es una regla de detención. Según esto, el entrevistador rechaza los primeros r − 1 solicitantes (deje que el solicitante M sea el mejor solicitante entre estos r − 1 solicitantes), y luego selecciona el primer solicitante posterior que sea mejor que el solicitante M. Se puede demostrar que la estrategia óptima se encuentra en esta clase de estrategias. (Tenga en cuenta que nunca debemos elegir un solicitante que no sea el mejor que hemos visto hasta ahora, ya que no puede ser el mejor solicitante en general). Para un límite arbitrario r, la probabilidad de que el mejor solicitante sea seleccionado es

${\displaystyle {\begin{aligned}P(r) ventaja=\sum ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ }i{\text{ is selected}}{\text{applicant }i{\text{ is the best}\right)\cdot P\left({\text{applicant }i{\text{ is the best}\right)\\cdot=\left[\sum ################################################################################################################################################################################################################################################################ {\begin{\begin{}{\text{\the best of the first }}i-1{\text{ applicants}\{\text{ is in the first }}r-1{ applicants}}\end{\text{applicant {\fn}\fn}\fn}\fnh}\cdot {\fn}\\\\fn}\\\\fn}\\fn}=\left[\sum] ¿Qué? {r-1}{i-1}\derecha]\cdot {\frac {1}{n}\\\\fn}\\\\fn}\\fn} {\fn}\fn}\\\\\cH0}\\fn}\cdot}\cdot {\cdot}\cdot}\cdot {\cdot}\cdot {\cdot {\cdot}\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot}}}\cdot {\cdot}\cdot {\cdot {\cdot {\fn}\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot {\cdot} {\cdot {\cdot {\cdot} {r-1}{n}\sum} ¿Qué? {1}{i-1}}$

La suma no se define para r = 1, pero en este caso la única política factible es seleccionar al primer solicitante, y por lo tanto P1) 1/n. Esta suma se obtiene notando que si el solicitante i es el mejor solicitante, entonces se selecciona si y sólo si el mejor solicitante entre el primero i − 1 solicitante es uno de los primeros r - 1 solicitantes que fueron rechazados. Letting n tiende a la infinidad, la escritura ${\displaystyle x}$ como límite (r.−1)/n, utilizando t para (i−1)/n y ♪ para 1/n, la suma puede ser aproximada por el integral

${\displaystyle P(x)=x\int ¿Por qué?$

Tomar el derivado de P()x) con respecto a ${\displaystyle x}$, establecerlo a 0, y resolver para x, encontramos que lo óptimo x es igual a 1/e. Así, el corte óptimo tiende a n/e como n aumentos, y el mejor solicitante es seleccionado con probabilidad 1/e.

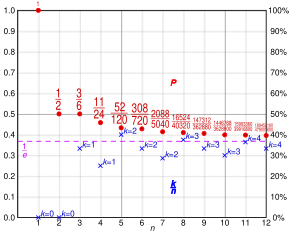
Para valores pequeños de n, el r óptimo también se puede obtener mediante métodos de programación dinámica estándar. Los umbrales óptimos r y la probabilidad de seleccionar la mejor alternativa P para varios valores de n se muestran en la siguiente tabla.

${\displaystyle n}$	1	2	3	4	5	6	7	8	9	10
${\displaystyle r}$	1	1	2	2	3	3	3	4	4	4
${\displaystyle P}$	1.000	0,50	0,50	0.458	0.433	0.428	0.414	0.410	0.406	0,399

La probabilidad de seleccionar al mejor solicitante en el problema de la secretaria clásica converge hacia ${\displaystyle 1/e\approx 0.368}$.

Solución alternativa

Este problema y varias modificaciones se pueden resolver (incluida la prueba de optimidad) de manera sencilla mediante el algoritmo de probabilidades, que también tiene otras aplicaciones. Las modificaciones del problema de la secretaria que pueden resolverse con este algoritmo incluyen disponibilidades aleatorias de los solicitantes, hipótesis más generales para que los solicitantes sean de interés para quien toma las decisiones, entrevistas grupales para los solicitantes, así como ciertos modelos para un número aleatorio de solicitantes.

Limitaciones

La solución del problema del secretario es sólo significativa si se justifica asumir que los solicitantes no tienen conocimiento de la estrategia de decisión empleada, porque los solicitantes tempranos no tienen ninguna oportunidad y no pueden aparecer de otra manera.

Un inconveniente importante para las aplicaciones de la solución del problema de la secretaria clásica es que el número de solicitantes ${\displaystyle n}$ debe ser conocido por adelantado, que rara vez es el caso. Una manera de superar este problema es suponer que el número de solicitantes es una variable aleatoria ${\displaystyle N}$ con una distribución conocida ${\displaystyle P(N=k)_{k=1,2,\cdots }$ (Presman and Sonin, 1972). Para este modelo, la solución óptima es en general mucho más difícil, sin embargo. Además, la probabilidad óptima de éxito ya no es alrededor de 1/e pero normalmente más bajo. Esto se puede entender en el contexto de tener un "precio" para pagar por no conocer el número de solicitantes. Sin embargo, en este modelo el precio es alto. Dependiendo de la elección de la distribución ${\displaystyle N}$, la probabilidad de ganar óptima puede acercarse a cero. La búsqueda de formas de hacer frente a este nuevo problema llevó a un nuevo modelo que rindió el llamado 1/e-law de la mejor elección.

1/e-law of best choice

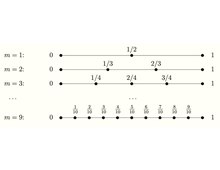
La esencia del modelo se basa en la idea de que la vida es secuencial y que los problemas del mundo real se plantean en tiempo real. Además, es más fácil estimar los tiempos en que eventos específicos (llegadas de solicitantes) deberían ocurrir con mayor frecuencia (si es que ocurren) que estimar la distribución del número de eventos específicos que ocurrirán. Esta idea condujo al siguiente enfoque, el llamado enfoque unificado (1984):

El modelo se define como sigue: Un solicitante debe ser seleccionado en algún intervalo de tiempo ${\displaystyle [0,T]}$ de un número desconocido ${\displaystyle N}$ de solicitantes clasificables. El objetivo es maximizar la probabilidad de seleccionar sólo lo mejor bajo la hipótesis de que todas las órdenes de llegada de diferentes rangos son igualmente probables. Supongamos que todos los solicitantes tienen lo mismo, pero independientes entre sí, la densidad del tiempo de llegada ${\displaystyle f}$ on ${\displaystyle [0,T]}$ y dejar ${\displaystyle F}$ denota la función de distribución del tiempo de llegada correspondiente, es decir

${\displaystyle F(t)=\int _{0} {t}f(s)ds}$, ${\displaystyle \,0\leq t\leq T}$.

Vamos. ${\displaystyle \tau }$ ser tal ${\displaystyle F(\tau)=1/e.}$ Considere la estrategia para esperar y observar a todos los solicitantes hasta el tiempo ${\displaystyle \tau }$ y luego seleccionar, si es posible, el primer candidato después del tiempo ${\displaystyle \tau }$ que es mejor que todos los anteriores. Entonces esta estrategia, llamada 1/e-strategy, tiene las siguientes propiedades:

La estrategia 1/e

i) rendimientos para todos ${\displaystyle N}$ una probabilidad de éxito de al menos 1/e,

ii) Es una estrategia minimax-optimal para el selector que no sabe ${\displaystyle N}$,

iii) selecciona, si hay por lo menos un solicitante, ninguno con probabilidad exactamente 1/e.

El 1/e-law, probado en 1984 por F. Thomas Bruss, fue una sorpresa. La razón era que un valor de aproximadamente 1/e había sido considerado antes como fuera de alcance en un modelo para desconocido ${\displaystyle N}$, mientras que este valor 1/e se logró ahora como un límite inferior para la probabilidad de éxito, y esto en un modelo con hipótesis posiblemente mucho más débil (véase, por ejemplo, Math. Comentarios 85:m).

Sin embargo, hay muchas otras estrategias que logran i) y ii) y, además, cumplen estrictamente mejor que la estrategia 1/e. simultáneamente para todos ${\displaystyle N}$Un ejemplo simple es la estrategia que selecciona (si es posible) el primer candidato relativamente mejor después del tiempo ${\displaystyle \tau }$ siempre que al menos un solicitante llegara antes de este momento, y de otro modo seleccione (si es posible) el segundo relativamente mejor candidato después del tiempo ${\displaystyle \tau }$.

El 1/e-law a veces se confunde con la solución para el problema del secretario clásico descrito anteriormente debido al papel similar del número 1/e. Sin embargo, en el 1/e-law, esta función es más general. El resultado también es más fuerte, ya que tiene para un número desconocido de solicitantes y ya que el modelo basado en una distribución del tiempo de llegada F es más susceptible para las solicitudes.

El juego del googol

En el artículo "¿Quién resolvió el problema del Secretario?" (Ferguson, 1989), se afirma que el problema de la secretaria apareció impreso por primera vez en la columna Mathematical Games de febrero de 1960 de Martin Gardner en Scientific American:

Pida a alguien que tome tantos resbalones de papel como quiera, y en cada resbalón escriba un número positivo diferente. Los números pueden variar de pequeñas fracciones de 1 a un número del tamaño de un googol (1 seguido de cien ceros) o incluso más grande. Estos resbalones se apagan la cara y se deslizan sobre la parte superior de una mesa. Una a la vez que das la cara a los resbalones. El objetivo es dejar de girar cuando llegas al número que crees que es el más grande de la serie. No puedes volver y escoger un resbalón con anterioridad. Si entregas todos los deslizamientos, entonces, por supuesto, debes elegir el último.

Ferguson señaló que el juego de la secretaria seguía sin resolverse, ya que era un juego de suma cero con dos jugadores antagónicos. En este juego:

• Alice, el jugador informado, escribe números en secreto distintos en ${\displaystyle n}$ tarjetas.
• Bob, el jugador de parada, observa los valores reales y puede dejar de girar las tarjetas cuando quiera, ganar si la última tarjeta girada tiene el número máximo general.
• Bob quiere adivinar el número máximo con la mayor probabilidad posible, mientras que el objetivo de Alice es mantener esta probabilidad lo más baja posible.

La diferencia con el problema básico de la secretaria son dos:

• Alice no tiene que escribir números uniformemente al azar. Puede escribirlos según cualquier distribución de probabilidad conjunta para engañar a Bob.
• Bob observa los valores reales escritos en las tarjetas, que puede utilizar en sus procedimientos de decisión.

Análisis estratégico

Alice escribe primero n números, que luego se encogieron. Entonces, su orden no importa, lo que significa que los números de Alice deben ser una secuencia variable intercambiable aleatoria ${\displaystyle X_{1},X_{2}, X_{n}$. La estrategia de Alice es elegir la secuencia variable aleatoria más difícil de cambiar.

La estrategia de Bob es formalizable como una regla de parar ${\displaystyle \tau }$ para la secuencia ${\displaystyle X_{1},X_{2}, X_{n}$.

Decimos que una regla de parar ${\displaystyle \tau }$ para Bob es un estrategia relativa para detener las filas sif depende sólo de las filas relativas de ${\displaystyle X_{1},X_{2}, X_{n}$, y no en sus valores numéricos. En otras palabras, es como si alguien interviniera en secreto después de que Alice escogiera sus números, y cambió cada número en ${\displaystyle X_{1},X_{2}, X_{n}$ en su rango relativo (lazos de ruptura al azar). Por ejemplo, ${\displaystyle 0,0.3,0.3,0.1}$ se cambia a ${\displaystyle 2,3,4}$ o ${\displaystyle 2,4,3,1}$ con igual probabilidad. Esto lo hace. como si Alice jugó una permutación aleatoria intercambiable en ${\displaystyle \{1,2,...,n\}$. Ahora, desde la única permutación aleatoria intercambiable en ${\displaystyle \{1,2,...,n\}$ es sólo la distribución uniforme sobre todas las permutaciones en ${\displaystyle \{1,2,...,n\}$, la estrategia óptima de parada de rango relativo es la regla de parada óptima para el problema de la secretaria, dada arriba, con una probabilidad ganadora

$${\displaystyle Pr(X_{\tau }=\max _{i\in 1:n}X_{i}=\max _{r\in 1:n}{\frac {r-1}{n}\sum ¿Qué? {1}{i-1}}$$

Por las reglas del juego, la secuencia de Alice debe ser intercambiable, pero para hacer bien en el juego, Alice no debe elegir que sea independiente. Si Alice muestra los números independientemente de alguna distribución fija, permitiría a Bob hacerlo mejor. Para ver esto intuitivamente, imagina si ${\displaystyle n=2}$, y Alice es elegir ambos números de la distribución normal ${\displaystyle N(0,1)}$Independientemente. Entonces si Bob gira un número y ve ${\displaystyle -3}$, entonces él puede dar una vuelta segura sobre el segundo número, y si Bob gira un número y ve ${\displaystyle +3}$Entonces puede elegir con confianza el primer número. Alice puede hacerlo mejor escogiendo ${\displaystyle ¿Qué?$ que están positivamente correlacionados.

Así pues, la declaración totalmente formal es la siguiente:

Existe una secuencia intercambiable de variables aleatorias ${\displaystyle X_{1},...$, tal para cualquiera Parar la regla ${\displaystyle \tau }$,

$${\displaystyle Pr(X_{\tau }=\max _{i\in 1:n}X_{i})\leq \max _{r\in 1:n}{\frac {r-1}{n}\sum ¿Qué? {1}{i-1}}$$

?

Solución

Para ${\displaystyle n=2}$, si Bob juega la estrategia óptima de paradas de rango relativo, entonces Bob tiene probabilidad de ganar 1/2. Sorprendentemente, Alice no tiene estrategia minimax, que está estrechamente relacionada con una paradoja de T. Cover y los dos sobres paradoja. Concretamente, Bob puede jugar esta estrategia: muestre un número aleatorio ${\displaystyle Sí.$. Si ${\displaystyle X_{1} Sí.$, entonces elija ${\displaystyle X_{1}$, más elegir ${\displaystyle X_{2}$. Ahora, Bob puede ganar con probabilidad estrictamente mayor que 1/2. Supongamos que los números de Alice son diferentes, entonces condicional en ${\displaystyle Y\not \in [\min(X_{1},X_{2}),\max(X_{1},X_{2})}$, Bob gana con probabilidad 1/2, pero condicional ${\displaystyle Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})}$Bob gana con probabilidad 1.

Note que el número al azar ${\displaystyle Sí.$ puede ser muestreado de cualquiera distribución aleatoria, mientras ${\displaystyle Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})}$ tiene probabilidad no cero.

Sin embargo, para cualquier ${\displaystyle \epsilon }$, Alice puede construir una secuencia intercambiable ${\displaystyle ¿Qué?$ tal que la probabilidad ganadora de Bob es en la mayoría ${\displaystyle 1/2+\epsilon }$.

Pero... ${\displaystyle n confiado2}$, la respuesta es sí: Alice puede elegir números aleatorios (que son variables aleatorias dependientes) de tal manera que Bob no puede jugar mejor que usar la estrategia clásica de parada basada en las filas relativas.

Rendimiento heurístico

El resto del artículo trata nuevamente el problema de la secretaria para un número conocido de solicitantes.

Stein, Seale & Rapoport 2003 derivó las probabilidades de éxito esperadas para varias heurísticas psicológicamente plausibles que podrían emplearse en el problema de la secretaria. Las heurísticas que examinaron fueron:

• La regla de corte (CR): No acepte ninguno de los primeros Sí. solicitantes; posteriormente, seleccione el primer candidato encontrado (es decir, un solicitante con rango relativo 1). Esta regla tiene como caso especial la política óptima para el problema del secretario clásico para el cual Sí. = r.
• Regla del conteo de candidatos (CCR): Seleccione Sí.- se encontró con candidato. Nota, que esta regla no salta necesariamente a ningún solicitante; sólo considera cuántos candidatos han sido observados, no cuán profundo es el encargado de la decisión en la secuencia del solicitante.
• Regla no candidata (SNCR): Seleccione el primer candidato encontrado después de observar Sí. no candidatos (es decir, solicitantes con rango relativo 1).

Cada heurista tiene un solo parámetro Sí.. La figura (shown on right) muestra las probabilidades de éxito esperadas para cada heurista como una función de Sí. para problemas con n = 80.

Cardenal payoff variante

Encontrar al mejor candidato puede parecer un objetivo bastante estricto. Uno puede imaginar que el entrevistador preferiría contratar a un solicitante de mayor valor que a uno de menor valor, y no preocuparse sólo por conseguir lo mejor. Es decir, el entrevistador obtendrá algún valor al seleccionar un solicitante que no es necesariamente el mejor, y el valor derivado aumenta con el valor del candidato seleccionado.

Para modelar este problema, supongamos que el ${\displaystyle n}$ los solicitantes tienen valores "verdaderos" que son variables aleatorias X dibujado i.i.d. de una distribución uniforme en [0, 1]. Similar al problema clásico descrito anteriormente, el entrevistador sólo observa si cada solicitante es el mejor hasta ahora (un candidato), debe aceptar o rechazar cada uno en el lugar, y Debe aceptar el último si es alcanzado. (Para ser claro, el entrevistador no aprende el rango relativo real cada uno solicitante. Sólo aprende si el solicitante tiene rango relativo 1.) Sin embargo, en esta versión la pago se da por el verdadero valor del solicitante seleccionado. Por ejemplo, si selecciona un solicitante cuyo valor verdadero es 0.8, entonces ganará 0.8. El objetivo del entrevistador es maximizar el valor esperado del solicitante seleccionado.

Puesto que los valores del solicitante son i.i.d. se deriva de una distribución uniforme en [0, 1], el valor esperado del ta solicitante dado que ${\displaystyle x_{t}=\max \left\{x_{1},x_{2},\ldotsx_{t}\right\}$ es dado por

${\displaystyle E_{t}=E\left(X_{t} imperi_{t}=1\right)={\frac {t}{t+1}}$

Como en el problema clásico, la política óptima es dada por un umbral, que para este problema denotaremos por ${\displaystyle c}$, en el que el entrevistador debe comenzar a aceptar candidatos. Bearden mostró que c o ${\displaystyle \lfloor {\sqrt {n}\rfloor$ o ${\displaystyle \lceil {\sqrt {n}\rceil}$. (De hecho, lo que sea más cercano a ${\displaystyle {\sqrt {n}}$) Esto se deriva del hecho de que dado un problema con ${\displaystyle n}$ solicitantes, el pago previsto para algunos umbrales arbitrarios ${\displaystyle 1\leq c\leq n}$ es

${\displaystyle V_{n}(c)=\sum ¿Por qué? ¿Por qué? {1}{t+1}\right)+\left[\prod] ¿Por qué? {1}{2}={\frac} {2cn-{c}{2}+c-n} {2cn}}$

Diferenciación ${\displaystyle V_{n}(c)}$ con respecto a c, uno se pone

${\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft} V. C}={\frac {\fnMicrosoft Sans Serif}$

Desde ${\displaystyle \partial ^{\,2}V/\partial c^{\,2}$ para todos los valores admisibles ${\displaystyle c}$, encontramos que ${\displaystyle V}$ se maximiza al máximo ${\displaystyle c={\sqrt {n}}$. Desde V es convexo en ${\displaystyle c}$, el umbral de valor entero óptimo debe ser ${\displaystyle \lfloor {\sqrt {n}\rfloor$ o ${\displaystyle \lceil {\sqrt {n}\rceil}$. Así, para la mayoría de los valores ${\displaystyle n}$ el entrevistador comenzará a aceptar a los solicitantes antes en la versión de pago cardinal que en la versión clásica donde el objetivo es seleccionar al mejor solicitante. Tenga en cuenta que este no es un resultado asintotico: Es para todos ${\displaystyle n}$. Sin embargo, esta no es la política óptima para maximizar el valor esperado de una distribución conocida. En el caso de una distribución conocida, el juego óptimo se puede calcular mediante programación dinámica.

Una forma más general de este problema introducida por Palley y Kremer (2014) supone que a medida que llega cada nuevo solicitante, el entrevistador observa su clasificación en relación con todos los solicitantes que han sido observados anteriormente. Este modelo es consistente con la noción de que un entrevistador aprende a medida que continúa el proceso de búsqueda acumulando un conjunto de puntos de datos anteriores que puede utilizar para evaluar nuevos candidatos a medida que llegan. Un beneficio de este llamado modelo de información parcial es que las decisiones y los resultados obtenidos dada la información de rango relativo se pueden comparar directamente con las decisiones y resultados óptimos correspondientes si al entrevistador se le hubiera dado información completa sobre el valor de cada solicitante. Este problema de información completa, en el que los solicitantes se seleccionan independientemente de una distribución conocida y el entrevistador busca maximizar el valor esperado del solicitante seleccionado, fue resuelto originalmente por Moser (1956), Sakaguchi (1961) y Karlin (1962).

Otras modificaciones

Existen varias variantes del problema de la secretaria que también tienen soluciones simples y elegantes.

Elige el segundo mejor, de un solo intento

Una variante reemplaza el deseo de escoger lo mejor con el deseo de escoger lo mejor. Robert J. Vanderbei llama a este problema "postdoc" argumentando que el "mejor" irá a Harvard. Para este problema, la probabilidad de éxito para un número incluso de solicitantes es exactamente ${\displaystyle {\frac {0.25n^{2}{n(n-1)}}$. Esta probabilidad tiende a 1/4 ya que n tiende a infinito ilustrando el hecho de que es más fácil elegir lo mejor que el segundo mejor.

Escoge los mejores, usando k intenta

Considere el problema de elegir los mejores secretarios de los candidatos, usando k Trys.

En general, el método de decisión óptimo comienza observando ${\displaystyle r=\left\lfloor {\frac Está bien. }$ candidatos sin elegir a ninguno de ellos, luego elegir cada candidato que es mejor que los primeros ${\displaystyle r}$ candidatos hasta que salgamos de candidatos o selecciones. Si ${\displaystyle k}$ se mantiene constante mientras ${\displaystyle n\to \infty }$, entonces la probabilidad del éxito converge a ${\displaystyle {\frac {}{ek}}} {\fnK}} {\fnK}}} {\fnK}}}}} {\fn}} {\fn}}}}} {\fnK}}}}}}}$. Por Vanderbei 1980, si ${\displaystyle k=n/2}$, entonces la probabilidad de éxito es ${\fnMicroc} {1}{n/2+1}}$.

Elija el mejor, utilizando varios intentos

En esta variante se permite un jugador ${\displaystyle r}$ elegir y ganar si alguna opción es la mejor. Una estrategia óptima para este problema pertenece a la clase de estrategias definidas por un conjunto de números de umbral ${\displaystyle (a_{1},a_{2},a_{r}}$, donde ${\displaystyle a_{1} confíaa_{2}\cdots$.

Específicamente, imagina que tienes ${\displaystyle r}$ Cartas de aceptación etiquetadas ${\displaystyle 1}$ a ${\displaystyle r}$. Lo habrías hecho. ${\displaystyle r}$ oficiales de la solicitud, cada uno con una carta. Sigues entrevistando a los candidatos y clasificarlos en un gráfico que cada oficial de solicitud puede ver. Ahora oficial ${\displaystyle i}$ enviaría su carta de aceptación al primer candidato que es mejor que todos los candidatos ${\displaystyle 1}$ a ${\displaystyle A_{i}$. (Las cartas de aceptación se dan por defecto a los últimos solicitantes, igual que en el problema de secretario estándar.)

At ${\displaystyle n\rightarrow \infty}$ límite, cada uno ${\displaystyle A_{i}\sim ne^{-k_{i}}$, para algún número racional ${\displaystyle K_{i}$.

Probabilidad de ganar

Cuando ${\displaystyle r=2}$, la probabilidad de ganar converge a ${\displaystyle e^{-1}+e^{-{\frac {3}}},(n\rightarrow \infty)}$. Más generalmente, para enteros positivos ${\displaystyle r}$, la probabilidad de ganar converge a ${\displaystyle p_{1}+p_{2}+\cdots #$, donde ${\displaystyle p_{i}=\lim _{n\rightarrow \infty }{\frac {a_{i} {n}}}} {a_{i}} {} {}} {}} {}}} {}}}} {}}}} {}}} {}}}}} {}}} {}}}}}} {}}}} {}}}}}}} {}}}}}} {}}}}}} {}}}}}}}} {} {}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}} {} {}}}}} {}}}}}}}} {}}}} {}}}}}}}}}}}}}} {}}}}}}}}} {} {}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$.

computado hasta ${\displaystyle r=4}$Con ${\displaystyle e^{-1}+e^{-{\frac {3}}+e^{-{\frac} {47}{\fn9}} {\fnMic {2761}{1152}}}} {\fnK}}} {\fn}}}}}}} {\fn9}}} {\fn9}}}}}}}} {\f}}}} {\f}}}}}}} {\fn\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}$.

Matsui & Ano 2016 dio un algoritmo general. Por ejemplo, ${\displaystyle {\fnMicroc {4162637}{1474560}}$.

Estudios experimentales

Los psicólogos y economistas experimentales han estudiado el comportamiento de decisión de personas reales en situaciones problemáticas de secretaria. En gran medida, este trabajo ha demostrado que las personas tienden a dejar de buscar demasiado pronto. Esto puede explicarse, al menos en parte, por el costo de evaluar a los candidatos. En entornos del mundo real, esto podría sugerir que las personas no buscan lo suficiente cuando se enfrentan a problemas en los que las alternativas de decisión se encuentran secuencialmente. Por ejemplo, al intentar decidir en qué gasolinera de una carretera detenerse para repostar, es posible que las personas no busquen lo suficiente antes de detenerse. De ser cierto, entonces tenderían a pagar más por la gasolina que si hubieran buscado por más tiempo. Lo mismo puede ocurrir cuando la gente busca billetes de avión en línea. La investigación experimental sobre problemas como el problema de la secretaria a veces se denomina investigación de operaciones conductuales.

Correlaciones neuronales

Si bien existe un cuerpo sustancial de investigación en neurociencia sobre la integración de información, o la representación de creencias, en tareas de toma de decisiones perceptuales que utilizan sujetos animales y humanos, se sabe relativamente poco sobre cómo se llega a la decisión de dejar de recopilar información. en.

Los investigadores han estudiado las bases neuronales para resolver el problema de la secretaria en voluntarios sanos mediante resonancia magnética funcional. Se utilizó un proceso de decisión de Markov (MDP) para cuantificar el valor de continuar buscando versus comprometerse con la opción actual. Las decisiones de tomar o rechazar una opción involucraron las cortezas prefrontales parietales y dorsolaterales, así como el cuerpo estriado ventral, la ínsula anterior y el cingulado anterior. Por lo tanto, las regiones del cerebro previamente implicadas en la integración de evidencia y la representación de recompensas codifican cruces de umbrales que desencadenan decisiones para comprometerse con una elección.

Historia

El problema de la secretaria aparentemente fue introducido en 1949 por Merrill M. Flood, quien lo llamó el problema de la prometida en una conferencia que dio ese año. Se refirió a él varias veces durante la década de 1950, por ejemplo, en una conferencia en Purdue el 9 de mayo de 1958, y finalmente se hizo ampliamente conocido en el folklore, aunque no se publicó nada en ese momento. En 1958 envió una carta a Leonard Gillman, con copias a una docena de amigos, entre ellos Samuel Karlin y J. Robbins, esbozando una prueba de la estrategia óptima, con un apéndice de R. Palermo que demostró que todas las estrategias están dominadas por una estrategia de la forma "rechazar el primer p incondicionalmente, luego aceptar al siguiente candidato que sea mejor".

La primera publicación fue aparentemente de Martin Gardner en Scientific American, febrero de 1960. Se había enterado de ello por John H. Fox Jr. y L. Gerald Marnie, quienes de forma independiente habían ideado un problema equivalente en 1958; lo llamaron el "juego del googol". Fox y Marnie no conocían la solución óptima; Gardner pidió consejo a Leo Moser, quien (junto con J. R. Pounder) proporcionó un análisis correcto para su publicación en la revista. Poco después, varios matemáticos escribieron a Gardner para contarle sobre el problema equivalente que habían escuchado a través de los rumores, todo lo cual probablemente se remonta al trabajo original de Flood.

La ley 1/e de mejor elección se debe a F. Thomas Bruss.

Ferguson tiene una extensa bibliografía y señala que un problema similar (pero diferente) había sido considerado por Arthur Cayley en 1875 e incluso por Johannes Kepler mucho antes, quien pasó 2 años investigando a 11 candidatos al matrimonio durante 1611-1613. tras la muerte de su primera esposa.

Generalización combinatoria

El problema de la secretaria se puede generalizar en el caso en que hay múltiples empleos diferentes. Otra vez, hay ${\displaystyle n}$ solicitantes que vienen en orden al azar. Cuando llega un candidato, revela un conjunto de números no negativos. Cada valor especifica su calificación para uno de los trabajos. El administrador no sólo tiene que decidir si debe tomar o no al solicitante, sino que, de ser así, también tiene que asignarla permanentemente a uno de los trabajos. El objetivo es encontrar una asignación donde la suma de calificaciones sea lo más grande posible. Este problema es idéntico a encontrar un peso máximo que coincida en un gráfico bipartito con peso de borde donde el ${\displaystyle n}$ nodos de un lado llegan en línea en orden aleatorio. Por lo tanto, es un caso especial del problema de emparejamiento bipartito en línea.

Mediante una generalización del algoritmo clásico para el problema de la secretaria, es posible obtener una asignación donde la suma esperada de calificaciones es sólo un factor de ${\displaystyle e}$ menos que una asignación óptima (offline).

Notas