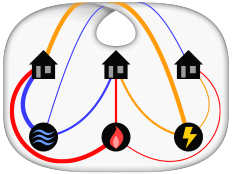
Problema de las tres utilidades

Diagrama de los tres problemas de utilidades mostrando líneas en un avión. ¿Puede cada casa conectarse a cada utilidad, sin cruce de líneas de conexión?

Dos vistas del gráfico de utilidad, también conocido como el gráfico Thomsen K3,3{displaystyle K_{3,3}

El rompecabezas matemático clásico conocido como el problema de los tres servicios públicos o, a veces, agua, gas y electricidad pide que se establezcan conexiones sin cruces entre tres casas y tres empresas de servicios públicos. en el avión. Al plantearlo a principios del siglo XX, Henry Dudeney escribió que ya era un viejo problema. Es un rompecabezas imposible: no es posible conectar las nueve líneas sin cruzarlas. Se pueden resolver versiones del problema sobre superficies no planas, como un toroide o una tira de Möbius, o que permiten que las conexiones pasen a través de otras casas o servicios públicos.

Este rompecabezas se puede formalizar como un problema en la teoría de gráficos topológicos preguntando si el gráfico bipartito completo K3,3{displaystyle K_{3,3}, con vértices que representan las casas y utilidades y bordes que representan sus conexiones, tiene un gráfico incrustando en el plano. La imposibilidad del rompecabezas corresponde al hecho de que K3,3{displaystyle K_{3,3} no es un gráfico plano. Se conocen múltiples pruebas de esta imposibilidad, y forman parte de la prueba del teorema de Kuratowski que caracteriza los gráficos planares por dos subgrafos prohibidos, uno de los cuales es K3,3{displaystyle K_{3,3}. La cuestión de minimizar el número de cruces en dibujos de gráficos bipartitos completos se conoce como problema de fábrica de ladrillos de Turán, y para K3,3{displaystyle K_{3,3} el número mínimo de cruces es uno.

K3,3{displaystyle K_{3,3} es un gráfico con seis vértices y nueve bordes, a menudo referido como gráfico de utilidad en referencia al problema. También se ha llamado Gráfico de Thomsen después del químico del siglo XIX Julius Thomsen. Es un gráfico bien cubierto, el gráfico cúbico más pequeño sin triángulo, y el gráfico mínimo no plana mínimamente rígido.

Historia

Kulman (1979) ofrece una revisión de la historia del problema de las tres utilidades. Afirma que la mayoría de las referencias publicadas sobre el problema lo caracterizan como "muy antiguo". En la primera publicación encontrada por Kullman, Henry Dudeney (1917) lo nombra "agua, gas y electricidad". Sin embargo, Dudeney afirma que el problema es "tan antiguo como las colinas... mucho más antiguo que la iluminación eléctrica o incluso el gas". Dudeney también publicó el mismo rompecabezas anteriormente, en The Strand Magazine en 1913. Un reclamo de prioridad en competencia es para Sam Loyd, quien fue citado por su hijo en una biografía póstuma por haber publicado el problema en 1900.

Otra versión temprana del problema consiste en conectar tres casas a tres pozos. Se establece de manera similar a un rompecabezas diferente (y solucionable) que también involucra tres casas y tres fuentes, con las tres fuentes y una casa tocando una pared rectangular; el acertijo nuevamente implica hacer conexiones que no se crucen, pero solo entre tres pares designados de casas y pozos o fuentes, como en los acertijos de enlaces numéricos modernos. El rompecabezas de Loyd 'Los vecinos pendencieros' de manera similar implica conectar tres casas a tres puertas por tres caminos que no se cruzan (en lugar de nueve como en el problema de los servicios públicos); una casa y las tres puertas están en la pared de un patio rectangular, que contiene las otras dos casas dentro de él.

Así como en el problema de tres utilidades, el gráfico K3,3{displaystyle K_{3,3} aparece a finales del siglo XIX y principios del siglo XX, tanto en estudios tempranos de rigidez estructural como en teoría de gráficos químicos, donde Julius Thomsen lo propuso en 1886 para la estructura entonces incierto de benceno. En honor al trabajo de Thomsen, K3,3{displaystyle K_{3,3} a veces se llama el gráfico Thomsen.

Declaración

El problema de las tres utilidades se puede enunciar de la siguiente manera:

Supongamos que tres casas necesitan estar conectadas a las empresas de agua, gas y electricidad, con una línea separada de cada casa a cada empresa. ¿Hay alguna manera de hacer las nueve conexiones sin ninguna de las líneas que se cruzan?

El problema es un acertijo matemático abstracto que impone restricciones que no existirían en una situación práctica de ingeniería. Su formalización matemática es parte del campo de la teoría topológica de grafos que estudia la incrustación de grafos en superficies. Una parte importante del acertijo, pero que a menudo no se menciona explícitamente en la redacción informal del acertijo, es que las casas, las empresas y las líneas deben colocarse en una superficie bidimensional con la topología de un plano, y que las líneas no pueden pasar por otros edificios; a veces esto se hace cumplir mostrando un dibujo de las casas y empresas, y pidiendo que las conexiones se dibujen como líneas en el mismo dibujo.

En términos más formales de teoría gráfica, el problema pregunta si el gráfico bipartito completo K3,3{displaystyle K_{3,3} es un gráfico plano. Este gráfico tiene seis vértices en dos subconjuntos de tres: un vértice para cada casa, y uno para cada utilidad. Tiene nueve bordes, un borde para cada uno de los pares de una casa con una utilidad, o más abstractamente un borde para cada par de un vértice en un subconjunto y un vértice en el otro subconjunto. Los gráficos plano son los gráficos que se pueden dibujar sin cruces en el plano, y si tal dibujo se puede encontrar, resolvería el rompecabezas de tres utilidades.

Soluciones de rompecabezas

Insolvencia

Prueba sin palabras: Una casa se elimina temporalmente. Las líneas que conectan las casas restantes con los servicios públicos dividen el avión en tres regiones. Sea cual sea la región en la que se coloca la casa eliminada, la utilidad similarmente sombreada está fuera de la región. Por el teorema curva Jordan, una línea que los conecta debe interseccionar una de las líneas existentes.

Como se presenta generalmente (en un plano plano bidimensional plano), la solución al rompecabezas de la utilidad es "no": no hay manera de hacer las nueve conexiones sin ninguna de las líneas que se cruzan entre sí. En otras palabras, el gráfico K3,3{displaystyle K_{3,3} no es plano. Kazimierz Kuratowski declaró en 1930 que K3,3{displaystyle K_{3,3} es no planario, de lo que sigue que el problema no tiene solución. Kullman (1979), sin embargo, afirma que "Lo suficientemente interesante, Kuratowski no publicó una prueba detallada de que [ K3,3{displaystyle K_{3,3} No es plano".

Una prueba de la imposibilidad de encontrar una incrustación planaria K3,3{displaystyle K_{3,3} utiliza un análisis de caso que involucra el teorema curva Jordan. En esta solución, se examinan diferentes posibilidades para las ubicaciones de los vértices con respecto a los 4 ciclos del gráfico y se muestra que todos son inconsistentes con una incrustación plana.

Alternativamente, es posible mostrar que cualquier gráfico bipartito sin puente con plano V{displaystyle V} vértices y E{displaystyle E} bordes tiene E≤ ≤ 2V− − 4{displaystyle Eleq 2V-4} combinando la fórmula Euler V− − E+F=2{displaystyle V-E+F=2} (donde) F{displaystyle F} es el número de caras de un embedding plano) con la observación de que el número de caras es a la mayoría de la mitad del número de bordes (los vértices alrededor de cada cara deben alternar entre casas y utilidades, por lo que cada cara tiene al menos cuatro bordes, y cada borde pertenece exactamente a dos caras). En el gráfico de utilidad, E=9{displaystyle E=9} y 2V− − 4=8{displaystyle 2V-4=8} así que en el gráfico de utilidad es falso que E≤ ≤ 2V− − 4{displaystyle Eleq 2V-4}. Debido a que no satisface esta desigualdad, el gráfico de utilidad no puede ser planificado.

Cambiando las reglas

Solución en un torus

Solución en una tira Möbius

K3,3{displaystyle K_{3,3} es un gráfico toroidal, lo que significa que puede ser incrustado sin cruces en un torus, una superficie del género uno. Estas incrustaciones resuelven las versiones del rompecabezas en el que las casas y las empresas se dibujan sobre una taza de café u otra superficie tal en lugar de un plano plano plano. Incluso hay suficiente libertad adicional en el torus para resolver una versión del rompecabezas con cuatro casas y cuatro utilidades. Del mismo modo, si el rompecabezas de tres utilidades se presenta en una hoja de material transparente, puede ser resuelto después de retorcer y pegar la hoja para formar una tira Möbius.

Otra forma de cambiar las reglas del acertijo para que sea solucionable, sugerida por Henry Dudeney, es permitir que las líneas de servicios públicos pasen a través de otras casas o servicios distintos de los que conectan.

Propiedades del gráfico de utilidad

Más allá del rompecabezas de la utilidad, el mismo gráfico K3,3{displaystyle K_{3,3} surge en varios otros contextos matemáticos, incluyendo la teoría de la rigidez, la clasificación de jaulas y gráficos bien cubiertos, el estudio de números de cruce de gráficos, y la teoría de los menores de grafito.

Rigidez

El gráfico de utilidad K3,3{displaystyle K_{3,3} es un gráfico Laman, lo que significa que para casi todas las colocaciones de sus vértices en el plano, no hay manera de mover continuamente sus vértices preservando todas las longitudes de borde, aparte de un movimiento rígido de todo el plano, y que ninguno de sus subgrafos de nalgas tiene la misma propiedad de rigidez. Es el ejemplo más pequeño de un gráfico Laman no plano. A pesar de ser un gráfico mínimamente rígido, tiene incrustaciones no rígidas con colocaciones especiales para sus vértices. Para las incrustaciones de posición general, una ecuación polinomio que describe todas las posibles colocaciones con las mismas longitudes de borde tiene el grado 16, lo que significa que en general puede haber en la mayoría de 16 colocaciones con las mismas longitudes. Es posible encontrar sistemas de longitudes de borde para los cuales hasta ocho de las soluciones a esta ecuación describen colocaciones realizables.

Otras propiedades de la teoría de grafos

K3,3{displaystyle K_{3,3} es un gráfico sin triángulo, en el que cada vértice tiene exactamente tres vecinos (un gráfico cúbico). Entre todos estos gráficos, es el más pequeño. Por lo tanto, es el (3,4)-cage, el gráfico más pequeño que tiene tres vecinos por vértice y en el que el ciclo más corto tiene la longitud cuatro.

Como todos los otros gráficos bipartitos completos, es un gráfico bien cubierto, lo que significa que cada conjunto máximo independiente tiene el mismo tamaño. En este gráfico, los únicos dos máximos conjuntos independientes son los dos lados de la bipartición, y son de igual tamaño. K3,3{displaystyle K_{3,3} es uno de sólo siete gráficos 3-regulares bien cubiertos.

Generalizaciones

Dibujo K3,3{displaystyle K_{3,3} con un cruce

Dos caracterizaciones importantes de gráficos plano, el teorema de Kuratowski que los gráficos plano son exactamente los gráficos que no contienen ninguno K3,3{displaystyle K_{3,3} ni el gráfico completo K5{displaystyle K_{5} como subdivisión, y el teorema de Wagner que los gráficos planar son exactamente los gráficos que no contienen ninguno K3,3{displaystyle K_{3,3} ni K5{displaystyle K_{5} como menor, utilizar y generalizar la no planificación K3,3{displaystyle K_{3,3}.

El "problema de fábrica de ladrillos" de Pál Turán pide más generalmente una fórmula para el número mínimo de cruces en un dibujo del gráfico bipartito completo Ka,b{displaystyle K_{a,b} en términos de los números de vértices a{displaystyle a} y b{displaystyle b} en los dos lados de la bipartición. El gráfico de utilidad K3,3{displaystyle K_{3,3} se puede dibujar con sólo un cruce, pero no con cero cruces, por lo que su número de cruce es uno.