Prismatoide

Prismatoide con caras paralelas A₁ y A₃, sección transversal intermedia A₂, y altura h

En geometría, un prismatoide es un poliedro cuyos vértices se encuentran todos en dos planos paralelos. Sus caras laterales pueden ser trapezoides o triángulos. Si ambos planos tienen el mismo número de vértices y las caras laterales son paralelogramos o trapecios, se llama prismoide.

Volumen

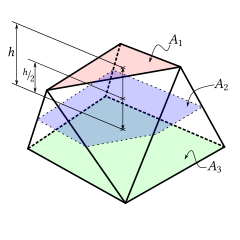
Si las áreas de las dos caras paralelas son A₁ y A₃, el área transversal de la intersección del prismatoide con un plano intermedio entre las dos caras paralelas es A₂, y la altura (la distancia entre las dos caras paralelas) es h, entonces el volumen del prismatoide es dado por ${displaystyle V={frac {h}+4A_{2}+A_{3}}{6}}}}}$(Esta fórmula sigue inmediatamente integrando el área paralela a los dos planos de vértices por la regla de Simpson, ya que esa regla es exacta para la integración de polinomios de grado hasta 3, y en este caso el área es en la mayoría de una función cuadrática en la altura.)

Familias prismatoides

Pirámides	Wedges	Paralepípedos	Prismas	Antiprismos			Cupolae	Frusta

Las familias de prismatoides incluyen:

• Pirámides, en las que un avión contiene sólo un punto;
• Wedges, en el que un avión contiene sólo dos puntos;
• Prismos, cuyos polígonos en cada plano son congruentes y se unen con rectángulos o paralelogramas;
• Antiprismos, cuyos polígonos en cada plano son congruentes y se unen por una franja alternante de triángulos;
• Anticipos de estrellas;
• Cupolae, en la que el polígono en un plano contiene el doble de puntos que el otro y se une a él por triángulos alternantes y rectángulos;
• Frusta obtenida por truncación de una pirámide;
• Prismatoides hexahedral de aspecto cuadrilátero:
  1. Paralepípedos – seis caras paralelas
  2. Rhombohedrons – seis caras de rombo
  3. Trigonal trapezohedra – seis caras congruentes
  4. Cuboides – seis caras rectangulares
  5. frusta cuadrilátero – una pirámide cuadrada de ápice
  6. Cubo – seis caras cuadradas

Dimensiones superiores

Una cúpula tetraedral-cuboctaedral.

En general, un politopo es prismatoidal si sus vértices existen en dos hiperplanos. Por ejemplo, en cuatro dimensiones, dos poliedros se pueden colocar en dos espacios tridimensionales paralelos y conectarse con lados poliédricos.