Principio de suma
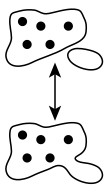
En combinatoria, la principio o Estado de la suma es un principio básico de contabilidad. Simplemente, es la idea intuitiva que si tenemos A Número de formas de hacer algo y B número de formas de hacer otra cosa y no podemos hacer ambas al mismo tiempo, entonces hay A+B{displaystyle A+B. maneras de elegir una de las acciones. En términos matemáticos, el principio de adición establece que, para conjuntos descomunales A y B, tenemos SilencioA∪ ∪ BSilencio=SilencioASilencio+SilencioBSilencio{displaystyle SilencioAcup B vidas= vivenA sobrevivirA sobrevivir.
La regla de la suma es un hecho sobre la teoría del conjunto.
El principio de adición puede extenderse a varios conjuntos. Si S1,S2,... ... ,Sn{displaystyle S_{1},S_{2},ldotsS_{n} son conjuntos descomunales pares, entonces tenemos:
Ejemplo sencillo

Una persona ha decidido hoy comprar en una tienda, ya sea en la parte norte o sur de la ciudad. Si visitan la parte norte de la ciudad, comprarán en un centro comercial, una mueblería o una joyería (3 formas). Si visitan la parte sur de la ciudad, comprarán en una tienda de ropa o en una zapatería (2 vías).
Así que hay 3+2=5{displaystyle 3+2=5} tiendas posibles que la persona podría terminar comprando hoy.
Principio de inclusión-exclusión
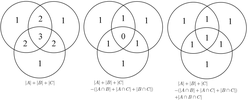
El principio de inclusión-exclusión (también conocido como principio de tamiz) puede considerarse como una generalización de la regla de la suma en el sentido de que también enumera el número de elementos en la unión de algunos conjuntos (pero no requiere que los conjuntos sean disjuntos). Afirma que si A1,..., An son conjuntos finitos, entonces
Principio de resta
Del mismo modo, para un determinado conjunto finito S, y dado otro conjunto A, si A⊂ ⊂ S{displaystyle Asubset S}Entonces SilencioAcSilencio=SilencioSSilencio− − SilencioASilencio{displaystyle SilencioA^{c}Principalmente. Para probar esto, note que SilencioAcSilencio+SilencioASilencio=SilencioSSilencio{displaystyle SilencioA^{c}Sobrevivir* por el principio adicional.
aplicaciones
El principio de adición se puede utilizar para probar la regla de Pascal combinatorialmente. Para calcular ()n+1k){displaystyle {binom {n+1}{k}}, se puede ver como el número de maneras de elegir k personas de una habitación que contiene n niños y 1 maestro. Entonces hay ()nk){displaystyle {binom {} {}} {fn}} {fn}}} {fn}} {fn}} maneras de elegir personas sin elegir al maestro, y ()nk− − 1){displaystyle {binom {n}{k-1}} maneras de elegir personas que incluyen al maestro. Así ()n+1k)=()nk)+()nk− − 1){binom} {binom} {binom}}={binom} {n}{k}+{binom} {n}{k-1}}.
El principio de adición también se puede utilizar para probar el principio de multiplicación.











