Principio de incertidumbre

AjustarCompartirImprimirCitar

Principio fundacional en la física cuántica

Regla de conmutación canónica para la posición q e impulso p variables de una partícula, 1927. pq − qp = h/2πi. Principio de incertidumbre de Heisenberg, 1927.

En la mecánica cuántica, el principio de incertidumbre (también conocido como principio de incertidumbre de Heisenberg) es cualquiera de una variedad de desigualdades matemáticas que establecen un límite fundamental para la Precisión con la que se pueden predecir los valores de ciertos pares de cantidades físicas de una partícula, como la posición, x y el momento, p, a partir de las condiciones iniciales.

Estos pares de variables se conocen como variables complementarias o variables canónicamente conjugadas; y, dependiendo de la interpretación, el principio de incertidumbre limita hasta qué punto tales propiedades conjugadas mantienen su significado aproximado, ya que el marco matemático de la física cuántica no admite la noción de propiedades conjugadas simultáneamente bien definidas expresadas por un solo valor. El principio de incertidumbre implica que, en general, no es posible predecir el valor de una cantidad con certeza arbitraria, incluso si se especifican todas las condiciones iniciales.

Introducido primero en 1927 por el físico alemán Werner Heisenberg, el principio de incertidumbre establece que cuanto más precisamente se determina la posición de una partícula, menos precisamente su impulso se puede predecir de las condiciones iniciales y viceversa. En el documento publicado en 1927, Heisenberg concluyó originalmente que el principio de incertidumbre era $Delta$ p $Delta$ q ~ h usando la constante de Planck completo. La desigualdad formal relacionada con la desviación estándar de posición σ_x y la desviación estándar del impulso σ_p fue derivado por Earle Hesse Kennard más tarde ese año y por Hermann Weyl en 1928:

$sigma _{x}sigma _{p}geq {frac {hbar }{2}}~~$

donde $ħ$ es la constante de Planck reducida, $h /(2 π$ ).

Históricamente, el principio de incertidumbre se ha confundido con un efecto relacionado en la física, llamado efecto del observador, que señala que las mediciones de ciertos sistemas no se pueden realizar sin afectar el sistema, es decir, sin cambiar algo en un sistema. Heisenberg utilizó tal efecto de observador a nivel cuántico (ver más abajo) como una "explicación" física; de la incertidumbre cuántica. Sin embargo, desde entonces ha quedado más claro que el principio de incertidumbre es inherente a las propiedades de todos los sistemas ondulatorios y que surge en la mecánica cuántica simplemente debido a la naturaleza ondulatoria de la materia de todos los objetos cuánticos. Por lo tanto, el principio de incertidumbre en realidad establece una propiedad fundamental de los sistemas cuánticos y no es una declaración sobre el éxito observacional de la tecnología actual. De hecho, el principio de incertidumbre tiene sus raíces en cómo aplicamos el cálculo para escribir las ecuaciones básicas de la mecánica. Debe enfatizarse que medida no significa solo un proceso en el que participa un físico-observador, sino cualquier interacción entre objetos clásicos y cuánticos independientemente de cualquier observador.

Dado que el principio de incertidumbre es un resultado tan básico en la mecánica cuántica, los experimentos típicos de la mecánica cuántica observan aspectos del mismo de manera rutinaria. Ciertos experimentos, sin embargo, pueden probar deliberadamente una forma particular del principio de incertidumbre como parte de su principal programa de investigación. Estos incluyen, por ejemplo, pruebas de relaciones de incertidumbre número-fase en sistemas superconductores o de óptica cuántica. Las aplicaciones que dependen del principio de incertidumbre para su funcionamiento incluyen tecnología de ruido extremadamente bajo, como la que se requiere en los interferómetros de ondas gravitacionales.

Introducción

La superposición de varias ondas de avión para formar un paquete de onda. Este paquete de onda se localiza cada vez más con la adición de muchas olas. El Fourier transforma es una operación matemática que separa un paquete de onda en sus ondas de avión individuales. Las ondas que se muestran aquí son reales para fines ilustrativos solamente, mientras que en la mecánica cuántica la función de onda es generalmente compleja.

Es fundamental ilustrar cómo se aplica el principio a situaciones físicas relativamente inteligibles, ya que es imperceptible en las escalas macroscópicas que experimentan los humanos. Dos marcos alternativos para la física cuántica ofrecen diferentes explicaciones para el principio de incertidumbre. La imagen de la mecánica ondulatoria del principio de incertidumbre es visualmente más intuitiva, pero la imagen más abstracta de la mecánica matricial lo formula de una manera que se generaliza más fácilmente.

Matemáticamente, en la mecánica ondulatoria, la relación de incertidumbre entre la posición y el momento surge porque las expresiones de la función de onda en las dos bases ortonormales correspondientes en el espacio de Hilbert son transformadas de Fourier entre sí (es decir, la posición y el momento son variables conjugadas). Una función distinta de cero y su transformada de Fourier no pueden localizarse claramente al mismo tiempo. Una compensación similar entre las varianzas de los conjugados de Fourier surge en todos los sistemas subyacentes al análisis de Fourier, por ejemplo, en las ondas de sonido: un tono puro es un pico agudo en una sola frecuencia, mientras que su transformada de Fourier da la forma de la onda de sonido en el tiempo. dominio, que es una onda sinusoidal completamente deslocalizada. En mecánica cuántica, los dos puntos clave son que la posición de la partícula toma la forma de una onda de materia, y el momento es su conjugado de Fourier, asegurado por la relación de De Broglie $p = ħk$ , donde $k$ es el número de onda.

En la mecánica matricial, la formulación matemática de la mecánica cuántica, cualquier par de operadores autoadjuntos que no conmutan y representan observables están sujetos a límites de incertidumbre similares. Un estado propio de un observable representa el estado de la función de onda para un determinado valor de medición (el valor propio). Por ejemplo, si se realiza una medición de un $A$ observable, entonces el sistema se encuentra en un estado propio particular $Ψ$ de ese observable. Sin embargo, el estado propio particular del observable $A$ no necesita ser un estado propio de otro observable $B$ : si es así, entonces no tiene una única medida asociada, ya que el sistema no está en un estado propio de ese observable.

Interpretación de la mecánica ondulatoria

(Referencia)

Ola de avión

Paquete de onda

Propagación de ondas de Broglie en 1d – parte real de la amplitud compleja es azul, parte imaginaria es verde. La probabilidad (como la opacidad del color) de encontrar la partícula en un punto dado x se extiende como una forma de onda, no hay una posición definida de la partícula. A medida que la amplitud aumenta sobre cero la curvatura revierte el signo, por lo que la amplitud comienza a disminuir de nuevo, y viceversa, el resultado es una amplitud alternante: una onda.

Según la hipótesis de Broglie, cada objeto en el universo es una ola, es decir, una situación que da lugar a este fenómeno. La posición de la partícula se describe por una función de onda $Psi (x,t)$ . La función de onda independiente del tiempo de una onda plana única de número de onda k₀ o impulso p₀ es

{displaystyle psi (x)propto e^{ik_{0}x}=e^{ip_{0}x/hbar }~.}

La regla de Born establece que esto debe interpretarse como una función de amplitud de densidad de probabilidad en el sentido de que la probabilidad de encontrar la partícula entre a y b es

{displaystyle operatorname {P} [aleq Xleq b]=int _{a}^{b}|psi (x)|^{2},mathrm {d} x~.}

En el caso de la onda de avión monomoded, $|psi (x)|^{2}$ es una distribución uniforme. En otras palabras, la posición de partículas es extremadamente incierta en el sentido de que podría ser esencialmente en cualquier lugar a lo largo del paquete de ondas.

Por otro lado, considere una función de onda que es una suma de muchas ondas, que podemos escribir como

{displaystyle psi (x)propto sum _{n}A_{n}e^{ip_{n}x/hbar }~,}

A_np_n

{displaystyle psi (x)={frac {1}{sqrt {2pi hbar }}}int _{-infty }^{infty }varphi (p)cdot e^{ipx/hbar },dp~,}

varphi (p)

varphi (p)

Transformación de Fourier

psi (x)

Una manera de cuantificar la precisión de la posición y el impulso es la desviación estándarσ. Desde $|psi (x)|^{2}$ es una función de densidad de probabilidad para la posición, calculamos su desviación estándar.

La precisión de la posición se mejora, es decir, se reduce σ_x, mediante el uso de muchas ondas planas, lo que debilita la precisión del impulso, es decir, se aumenta σ_p. Otra forma de decir esto es que σ_x y σ_p tienen una relación inversa o al menos están acotados desde abajo. Este es el principio de incertidumbre, cuyo límite exacto es el límite de Kennard. Haga clic en el botón mostrar a continuación para ver una derivación semiformal de la desigualdad de Kennard utilizando la mecánica ondulatoria.

Proof of the Kennard inequality using wave mechanics

We are interested in the variances of position and momentum, defined as

{displaystyle sigma _{x}^{2}=int _{-infty }^{infty }x^{2}cdot |psi (x)|^{2},dx-left(int _{-infty }^{infty }xcdot |psi (x)|^{2},dxright)^{2}}

{displaystyle sigma _{p}^{2}=int _{-infty }^{infty }p^{2}cdot |varphi (p)|^{2},dp-left(int _{-infty }^{infty }pcdot |varphi (p)|^{2},dpright)^{2}~.}

Without loss of generality, we will assume that the means vanish, which just amounts to a shift of the origin of our coordinates. (A more general proof that does not make this assumption is given below.) This gives us the simpler form

{displaystyle sigma _{x}^{2}=int _{-infty }^{infty }x^{2}cdot |psi (x)|^{2},dx}

{displaystyle sigma _{p}^{2}=int _{-infty }^{infty }p^{2}cdot |varphi (p)|^{2},dp~.}

The function $f(x)=xcdot psi (x)$ can be interpreted as a vector in a function space. We can define an inner product for a pair of functions u(x) and v(x) in this vector space:

{displaystyle langle umid vrangle =int _{-infty }^{infty }u^{*}(x)cdot v(x),dx,}

where the asterisk denotes the complex conjugate.

With this inner product defined, we note that the variance for position can be written as

{displaystyle sigma _{x}^{2}=int _{-infty }^{infty }|f(x)|^{2},dx=langle fmid frangle ~.}

We can repeat this for momentum by interpreting the function ${displaystyle {tilde {g}}(p)=pcdot varphi (p)}$ as a vector, but we can also take advantage of the fact that $psi (x)$ and $varphi (p)$ are Fourier transforms of each other. We evaluate the inverse Fourier transform through integration by parts:

{displaystyle {begin{aligned}g(x)&={frac {1}{sqrt {2pi hbar }}}cdot int _{-infty }^{infty }{tilde {g}}(p)cdot e^{ipx/hbar },dp\&={frac {1}{sqrt {2pi hbar }}}int _{-infty }^{infty }pcdot varphi (p)cdot e^{ipx/hbar },dp\&={frac {1}{2pi hbar }}int _{-infty }^{infty }left[pcdot int _{-infty }^{infty }psi (chi)e^{-ipchi /hbar },dchi right]cdot e^{ipx/hbar },dp\&={frac {i}{2pi }}int _{-infty }^{infty }left[{cancel {left.psi (chi)e^{-ipchi /hbar }right|_{-infty }^{infty }}}-int _{-infty }^{infty }{frac {dpsi (chi)}{dchi }}e^{-ipchi /hbar },dchi right]cdot e^{ipx/hbar },dp\&={frac {-i}{2pi }}int _{-infty }^{infty }int _{-infty }^{infty }{frac {dpsi (chi)}{dchi }}e^{-ipchi /hbar },dchi ,e^{ipx/hbar },dp\&=left(-ihbar {frac {d}{dx}}right)cdot psi (x),end{aligned}}}

where the canceled term vanishes because the wave function vanishes at infinity. Often the term

{textstyle -ihbar {frac {d}{dx}}}

is called the momentum operator in position space. Applying Parseval's theorem, we see that the variance for momentum can be written as

{displaystyle sigma _{p}^{2}=int _{-infty }^{infty }|{tilde {g}}(p)|^{2},dp=int _{-infty }^{infty }|g(x)|^{2},dx=langle gmid grangle.}

The Cauchy–Schwarz inequality asserts that

{displaystyle sigma _{x}^{2}sigma _{p}^{2}=langle fmid frangle cdot langle gmid grangle geq |langle fmid grangle |^{2}~.}

The modulus squared of any complex number z can be expressed as

{displaystyle |z|^{2}={Big (}{text{Re}}(z){Big)}^{2}+{Big (}{text{Im}}(z){Big)}^{2}geq {Big (}{text{Im}}(z){Big)}^{2}=left({frac {z-z^{ast }}{2i}}right)^{2}.}

we let

z=langle f|grangle

and

{displaystyle z^{*}=langle gmid frangle }

and substitute these into the equation above to get

{displaystyle |langle fmid grangle |^{2}geq left({frac {langle fmid grangle -langle gmid frangle }{2i}}right)^{2}~.}

All that remains is to evaluate these inner products.

{displaystyle {begin{aligned}langle fmid grangle -langle gmid frangle ={}&int _{-infty }^{infty }psi ^{*}(x),xcdot left(-ihbar {frac {d}{dx}}right),psi (x),dx\&{}-int _{-infty }^{infty }psi ^{*}(x),left(-ihbar {frac {d}{dx}}right)cdot x,psi (x),dx\={}&ihbar cdot int _{-infty }^{infty }psi ^{*}(x)left[left(-xcdot {frac {dpsi (x)}{dx}}right)+{frac {d(xpsi (x))}{dx}}right],dx\={}&ihbar cdot int _{-infty }^{infty }psi ^{*}(x)left[left(-xcdot {frac {dpsi (x)}{dx}}right)+psi (x)+left(xcdot {frac {dpsi (x)}{dx}}right)right],dx\={}&ihbar cdot int _{-infty }^{infty }psi ^{*}(x)psi (x),dx\={}&ihbar cdot int _{-infty }^{infty }|psi (x)|^{2},dx\={}&ihbar end{aligned}}}

Plugging this into the above inequalities, we get

{displaystyle sigma _{x}^{2}sigma _{p}^{2}geq |langle fmid grangle |^{2}geq left({frac {langle fmid grangle -langle gmid frangle }{2i}}right)^{2}=left({frac {ihbar }{2i}}right)^{2}={frac {hbar ^{2}}{4}}}

or taking the square root

{displaystyle sigma _{x}sigma _{p}geq {frac {hbar }{2}}~.}

Note that the only physics involved in this proof was that $psi (x)$ and $varphi (p)$ are wave functions for position and momentum, which are Fourier transforms of each other. A similar result would hold for any pair of conjugate variables.

Interpretación de la mecánica de matrices

(Referencia)

En los mecánicos de matriz, observables como la posición y el impulso están representados por operadores autónomos. Al considerar pares de observables, una cantidad importante es la conmutador. Para un par de operadores $#$ y ${hat {B}}$ , uno define su conmutador como

{displaystyle [{hat {A}},{hat {B}}]={hat {A}}{hat {B}}-{hat {B}}{hat {A}}.}

{displaystyle [{hat {x}},{hat {p}}]=ihbar.}

El significado físico de la no-commutatividad se puede entender considerando el efecto del conmutador en la posición y el impulso eigenstats. Vamos $|psi rangle$ ser un eigenstat derecho de posición con un eigenvalue constante $x 0$ . Por definición, esto significa que ${hat {x}}|psi rangle =x_{0}|psi rangle.$ Aplicar el conmutador a $|psi rangle$ rendimientos

{displaystyle [{hat {x}},{hat {p}}]|psi rangle =({hat {x}}{hat {p}}-{hat {p}}{hat {x}})|psi rangle =({hat {x}}-x_{0}{hat {I}}){hat {p}},|psi rangle =ihbar |psi rangle}

Î

Supongamos, por el bien de la prueba por contradicción, que $|psi rangle$ es también un correcto eigenstat de impulso, con constante eigenvalue $p 0$ . Si esto fuera cierto, entonces uno podría escribir

{displaystyle ({hat {x}}-x_{0}{hat {I}}){hat {p}},|psi rangle =({hat {x}}-x_{0}{hat {I}})p_{0},|psi rangle =(x_{0}{hat {I}}-x_{0}{hat {I}})p_{0},|psi rangle =0.}

{displaystyle [{hat {x}},{hat {p}}]|psi rangle =ihbar |psi rangle neq 0.}

Cuando se mide un estado, se proyecta en un estado propio en base al observable relevante. Por ejemplo, si se mide la posición de una partícula, entonces el estado equivale a un estado propio de posición. Sin embargo, esto significa que el estado no es un estado propio de cantidad de movimiento, sino que puede representarse como una suma de múltiples estados propios de base de cantidad de movimiento. En otras palabras, el impulso debe ser menos preciso. Esta precisión puede ser cuantificada por las desviaciones estándar,

{displaystyle sigma _{x}={sqrt {langle {hat {x}}^{2}rangle -langle {hat {x}}rangle ^{2}}}}

{displaystyle sigma _{p}={sqrt {langle {hat {p}}^{2}rangle -langle {hat {p}}rangle ^{2}}}.}

Al igual que en la interpretación anterior de la mecánica ondulatoria, se ve una compensación entre las respectivas precisiones de los dos, cuantificada por el principio de incertidumbre.

Límite de Heisenberg

En metrología cuántica, y especialmente en interferometría, el límite de Heisenberg es la tasa óptima a la que la precisión de una medición puede escalar con la energía utilizada en la medición. Normalmente, esta es la medida de una fase (aplicada a un brazo de un divisor de haz) y la energía viene dada por el número de fotones utilizados en un interferómetro. Aunque algunos afirman haber superado el límite de Heisenberg, esto refleja un desacuerdo sobre la definición del recurso de escala. Definido adecuadamente, el límite de Heisenberg es una consecuencia de los principios básicos de la mecánica cuántica y no se puede superar, aunque se puede superar el límite débil de Heisenberg.

Relaciones de incertidumbre de Robertson-Schrödinger

La forma general más común del principio de incertidumbre es la relación de incertidumbre de Robertson.

Para un operador Hermitian arbitrario ${hat {mathcal {O}}}$ podemos asociar una desviación estándar

{displaystyle sigma _{mathcal {O}}={sqrt {langle {hat {mathcal {O}}}^{2}rangle -langle {hat {mathcal {O}}}rangle ^{2}}},}

langle {mathcal {O}}rangle

{hat {A}}

{hat {B}}

conmutador

{displaystyle [{hat {A}},{hat {B}}]={hat {A}}{hat {B}}-{hat {B}}{hat {A}},}

En esta notación, la relación de incertidumbre de Robertson viene dada por

{displaystyle sigma _{A}sigma _{B}geq left|{frac {1}{2i}}langle [{hat {A}},{hat {B}}]rangle right|={frac {1}{2}}left|langle [{hat {A}},{hat {B}}]rangle right|,}

La relación de incertidumbre de Robertson se deriva inmediatamente de una desigualdad un poco más fuerte, la relación de incertidumbre de Schrödinger,

${displaystyle sigma _{A}^{2}sigma _{B}^{2}geq left|{frac {1}{2}}langle {{hat {A}},{hat {B}}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle right|^{2}+left|{frac {1}{2i}}langle [{hat {A}},{hat {B}}]rangle right|^{2},}$

donde hemos introducido el anticonmutador,

{displaystyle {{hat {A}},{hat {B}}}={hat {A}}{hat {B}}+{hat {B}}{hat {A}}.}

Prueba de la relación de incertidumbre Schrödinger

La derivación que se muestra aquí incorpora y construye de los que se muestran en Robertson, Schrödinger y libros de texto estándar como Griffiths. Para cualquier operador Hermitian ${hat {A}}$ , basado en la definición de varianza, tenemos

{displaystyle sigma _{A}^{2}=langle ({hat {A}}-langle {hat {A}}rangle)Psi |({hat {A}}-langle {hat {A}}rangle)Psi rangle.}

Dejamos

|frangle =|({hat {A}}-langle {hat {A}}rangle)Psi rangle

y así

{displaystyle sigma _{A}^{2}=langle fmid frangle ,.}

Del mismo modo, para cualquier otro operador Hermitiano ${hat {B}}$ en el mismo estado

{displaystyle sigma _{B}^{2}=langle ({hat {B}}-langle {hat {B}}rangle)Psi |({hat {B}}-langle {hat {B}}rangle)Psi rangle =langle gmid grangle }

para

|grangle=|(hat{B}-langle hat{B} rangle)Psi rangle.

El producto de las dos desviaciones se puede expresar así como

{displaystyle sigma _{A}^{2}sigma _{B}^{2}=langle fmid frangle langle gmid grangle.}

()1)

Para relacionar los dos vectores $|frangle$ y $|grangle$ , utilizamos la desigualdad Cauchy-Schwarz que se define como

{displaystyle langle fmid frangle langle gmid grangle geq |langle fmid grangle |^{2},}

y, por consiguiente, Ecuación (Ecuación)1) puede ser escrito como

{displaystyle sigma _{A}^{2}sigma _{B}^{2}geq |langle fmid grangle |^{2}.}

()2)

Desde ${displaystyle langle fmid grangle }$ es en general un número complejo, utilizamos el hecho de que el módulo cuadrado de cualquier número complejo $z$ se define como ${displaystyle |z|^{2}=zz^{*}}$ , donde $z^{*}$ es el complejo conjugado de $z$ . El módulo cuadrado también se puede expresar como

{displaystyle |z|^{2}={Big (}operatorname {Re} (z){Big)}^{2}+{Big (}operatorname {Im} (z){Big)}^{2}={Big (}{frac {z+z^{ast }}{2}}{Big)}^{2}+{Big (}{frac {z-z^{ast }}{2i}}{Big)}^{2}.}

()3)

Dejamos ${displaystyle z=langle fmid grangle }$ y ${displaystyle z^{*}=langle gmid frangle }$ y sustituir estos en la ecuación anterior para conseguir

{displaystyle |langle fmid grangle |^{2}={bigg (}{frac {langle fmid grangle +langle gmid frangle }{2}}{bigg)}^{2}+{bigg (}{frac {langle fmid grangle -langle gmid frangle }{2i}}{bigg)}^{2}}

()4)

El producto interior ${displaystyle langle fmid grangle }$ está escrito explícitamente como

{displaystyle langle fmid grangle =langle ({hat {A}}-langle {hat {A}}rangle)Psi |({hat {B}}-langle {hat {B}}rangle)Psi rangle}

y utilizando el hecho de que

{hat {A}}

{hat {B}}

son operadores ermitianos, encontramos

{displaystyle {begin{aligned}langle fmid grangle &=langle Psi |({hat {A}}-langle {hat {A}}rangle)({hat {B}}-langle {hat {B}}rangle)Psi rangle \[4pt]&=langle Psi mid ({hat {A}}{hat {B}}-{hat {A}}langle {hat {B}}rangle -{hat {B}}langle {hat {A}}rangle +langle {hat {A}}rangle langle {hat {B}}rangle)Psi rangle \[4pt]&=langle Psi mid {hat {A}}{hat {B}}Psi rangle -langle Psi mid {hat {A}}langle {hat {B}}rangle Psi rangle -langle Psi mid {hat {B}}langle {hat {A}}rangle Psi rangle +langle Psi mid langle {hat {A}}rangle langle {hat {B}}rangle Psi rangle \[4pt]&=langle {hat {A}}{hat {B}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle +langle {hat {A}}rangle langle {hat {B}}rangle \[4pt]&=langle {hat {A}}{hat {B}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle.end{aligned}}}

Del mismo modo se puede demostrar que ${displaystyle langle gmid frangle =langle {hat {B}}{hat {A}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle.}$

Así, tenemos

{displaystyle langle fmid grangle -langle gmid frangle =langle {hat {A}}{hat {B}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle -langle {hat {B}}{hat {A}}rangle +langle {hat {A}}rangle langle {hat {B}}rangle =langle [{hat {A}},{hat {B}}]rangle }

{displaystyle langle fmid grangle +langle gmid frangle =langle {hat {A}}{hat {B}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle +langle {hat {B}}{hat {A}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle =langle {{hat {A}},{hat {B}}}rangle -2langle {hat {A}}rangle langle {hat {B}}rangle.}

Ahora sustituimos las dos ecuaciones anteriores arriba en Eq. (4) y conseguir

{displaystyle |langle fmid grangle |^{2}={Big (}{frac {1}{2}}langle {{hat {A}},{hat {B}}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle {Big)}^{2}+{Big (}{frac {1}{2i}}langle [{hat {A}},{hat {B}}]rangle {Big)}^{2},.}

Sustituir lo anterior a la ecuación (Ecuación)2) tenemos la relación de incertidumbre Schrödinger

{displaystyle sigma _{A}sigma _{B}geq {sqrt {{Big (}{frac {1}{2}}langle {{hat {A}},{hat {B}}}rangle -langle {hat {A}}rangle langle {hat {B}}rangle {Big)}^{2}+{Big (}{frac {1}{2i}}langle [{hat {A}},{hat {B}}]rangle {Big)}^{2}}}.}

Esta prueba tiene un problema relacionado con los dominios de los operadores involucrados. Para que la prueba tenga sentido, el vector ${hat {B}}|Psi rangle$ tiene que estar en el dominio del operador sin límites ${hat {A}}$ , que no es siempre el caso. De hecho, la relación de incertidumbre de Robertson es falsa si ${hat {A}}$ es una variable de ángulo y ${hat {B}}$ es el derivado con respecto a esta variable. En este ejemplo, el conmutador es una constante no cero —como en la relación de incertidumbre de Heisenberg— y sin embargo hay estados donde el producto de las incertidumbres es cero. (Véase la sección del contraejemplo a continuación.) Este problema se puede superar utilizando un método de variación para la prueba, o trabajando con una versión exponente de las relaciones de conmutación canónica.

Tenga en cuenta que en la forma general de la relación de incertidumbre Robertson-Schrödinger, no hay necesidad de asumir que los operadores ${hat {A}}$ y ${hat {B}}$ son operadores autónomos. Basta asumir que son meramente operadores simétricos. (La distinción entre estas dos nociones es generalmente enlucida en la literatura física, donde el término Hermitian se utiliza para o ambas clases de operadores. Véase el capítulo 9 del libro de Hall para una discusión detallada de esta importante pero técnica distinción.)

Estados mixtos

La relación de incertidumbre de Robertson-Schrödinger puede generalizarse de forma directa para describir estados mixtos.

{displaystyle sigma _{A}^{2}sigma _{B}^{2}geq left|{frac {1}{2}}operatorname {tr} (rho {A,B})-operatorname {tr} (rho A)operatorname {tr} (rho B)right|^{2}+left|{frac {1}{2i}}operatorname {tr} (rho [A,B])right|^{2}.}

Las relaciones de incertidumbre Maccone-Pati

La relación de incertidumbre Robertson-Schrödinger puede ser trivial si el estado del sistema es elegido para ser eigenstat de uno de los observables. Las relaciones de incertidumbre más fuertes probadas por Maccone y Pati dan límites no-triviales a la suma de las diferencias para dos observables incompatibles. (Los trabajos adicionales sobre relaciones de incertidumbre formuladas como la suma de diferencias incluyen, por ejemplo, Ref. debido a Huang.) Para dos observables no transmutadores $A$ y $B$ la primera relación de incertidumbre más fuerte es dada por

{displaystyle sigma _{A}^{2}+sigma _{B}^{2}geq pm ilangle Psi mid [A,B]|Psi rangle +mid langle Psi mid (Apm iB)mid {bar {Psi }}rangle |^{2},}

{displaystyle sigma _{A}^{2}=langle Psi |A^{2}|Psi rangle -langle Psi mid Amid Psi rangle ^{2}}

{displaystyle sigma _{B}^{2}=langle Psi |B^{2}|Psi rangle -langle Psi mid Bmid Psi rangle ^{2}}

{displaystyle |{bar {Psi }}rangle }

{displaystyle |Psi rangle }

{displaystyle pm ilangle Psi mid [A,B]mid Psi rangle }

La segunda relación de incertidumbre más fuerte viene dada por

{displaystyle sigma _{A}^{2}+sigma _{B}^{2}geq {frac {1}{2}}|langle {bar {Psi }}_{A+B}mid (A+B)mid Psi rangle |^{2}}

{displaystyle |{bar {Psi }}_{A+B}rangle }

|Psi rangle

{displaystyle |{bar {Psi }}_{A+B}rangle }

{displaystyle |Psi rangle }

{displaystyle (A+B)}

{displaystyle |Psi rangle }

{displaystyle (A+B)}

A

B

|Psi rangle

|Psi rangle

Mejora de la relación de incertidumbre de Robertson-Schrödinger basada en descomposiciones de la matriz de densidad

La incertidumbre Robertson-Schrödinger se puede mejorar notando que debe mantener para todos los componentes ${displaystyle varrho _{k}}$ en cualquier descomposición de la matriz de densidad dada como

{displaystyle varrho =sum _{k}p_{k}varrho _{k}.}

{displaystyle p_{k}geq 0}

{displaystyle sum _{k}p_{k}=1}

{displaystyle sum _{k}a_{k}sum _{k}b_{k}geq left(sum _{k}{sqrt {a_{k}b_{k}}}right)^{2}}

{displaystyle a_{k},b_{k}geq 0}

{displaystyle sigma _{A}^{2}sigma _{B}^{2}geq left[sum _{k}p_{k}L(varrho _{k})right]^{2},}

{displaystyle L(varrho)={sqrt {left|{frac {1}{2}}operatorname {tr} (rho {A,B})-operatorname {tr} (rho A)operatorname {tr} (rho B)right|^{2}+left|{frac {1}{2i}}operatorname {tr} (rho [A,B])right|^{2}}}.}

{displaystyle sigma _{A}^{2}sigma _{B}^{2}geq left[max _{p_{k},varrho _{k}}sum _{k}p_{k}L(varrho _{k})right]^{2},}

Con argumentos similares, se puede derivar una relación con un techo convexo en el lado derecho

{displaystyle sigma _{A}^{2}F_{Q}[varrhoB]geq 4left[min _{p_{k},Psi _{k}}sum _{k}p_{k}L(vert Psi _{k}rangle langle Psi _{k}vert)right]^{2}}

{displaystyle F_{Q}[varrhoB]}

{displaystyle varrho =sum _{k}p_{k}vert Psi _{k}rangle langle Psi _{k}vert.}

Sigue una desigualdad más simple sin un techo convexo

{displaystyle sigma _{A}^{2}F_{Q}[varrhoB]geq vert langle i[A,B]rangle vert ^{2},}

{displaystyle F_{Q}[varrhoB]leq 4sigma _{B},}

Espacio de fase

En la formulación del espacio de fase de la mecánica cuántica, la relación Robertson-Schrödinger sigue de una condición de positividad a una función real de la estrella-cuadra. Dada una función Wigner $W(x,p)$ con producto estrella ★ y una función f, lo siguiente es generalmente cierto:

{displaystyle langle f^{*}star frangle =int (f^{*}star f),W(x,p),dx,dpgeq 0~.}

Elegir ${displaystyle f=a+bx+cp}$ , llegamos a

{displaystyle langle f^{*}star frangle ={begin{bmatrix}a^{*}&b^{*}&c^{*}end{bmatrix}}{begin{bmatrix}1&langle xrangle &langle prangle \langle xrangle &langle xstar xrangle &langle xstar prangle \langle prangle &langle pstar xrangle &langle pstar prangle end{bmatrix}}{begin{bmatrix}a\b\cend{bmatrix}}geq 0~.}

Dado que esta condición de positividad es cierta para todos a, b y c, se deduce que todos los valores propios de la matriz no son negativos.

Los valores propios no negativos implican una condición de no negatividad correspondiente en el determinante,

{displaystyle det {begin{bmatrix}1&langle xrangle &langle prangle \langle xrangle &langle xstar xrangle &langle xstar prangle \langle prangle &langle pstar xrangle &langle pstar prangle end{bmatrix}}=det {begin{bmatrix}1&langle xrangle &langle prangle \langle xrangle &langle x^{2}rangle &leftlangle xp+{frac {ihbar }{2}}rightrangle \langle prangle &leftlangle xp-{frac {ihbar }{2}}rightrangle &langle p^{2}rangle end{bmatrix}}geq 0~,}

{displaystyle sigma _{x}^{2}sigma _{p}^{2}=left(langle x^{2}rangle -langle xrangle ^{2}right)left(langle p^{2}rangle -langle prangle ^{2}right)geq left(langle xprangle -langle xrangle langle prangle right)^{2}+{frac {hbar ^{2}}{4}}~.}

Ejemplos

Dado que las relaciones de Robertson y Schrödinger son para operadores generales, las relaciones se pueden aplicar a dos observables cualquiera para obtener relaciones de incertidumbre específicas. Algunas de las relaciones más comunes que se encuentran en la literatura se dan a continuación.

Para la posición y el impulso lineal, la relación de conmutación canónica ${displaystyle [{hat {x}},{hat {p}}]=ihbar }$ implica la desigualdad Kennard de arriba: ${displaystyle sigma _{x}sigma _{p}geq {frac {hbar }{2}}.}$
Para dos componentes ortogonales del motor angular total de un objeto: ${displaystyle sigma _{J_{i}}sigma _{J_{j}}geq {frac {hbar }{2}}{big |}langle J_{k}rangle {big |},}$ Donde i, j, k son distintos, y J_i denota el impulso angular a lo largo del x_i Axis. Esta relación implica que a menos que los tres componentes se desvanezcan juntos, sólo un componente único del impulso angular de un sistema se puede definir con precisión arbitraria, normalmente el componente paralelo a un campo externo (magnético o eléctrico). Además, para ${displaystyle [J_{x},J_{y}]=ihbar varepsilon _{xyz}J_{z}}$ , una opción ${displaystyle {hat {A}}=J_{x}}$ , ${displaystyle {hat {B}}=J_{y}}$ , en multiples de impulso angular, ↑ = Silencioj, m################################################################################################################################################################################################################################################################ ${displaystyle langle J_{x}^{2}+J_{y}^{2}+J_{z}^{2}rangle }$ ) de abajo y así produce limitaciones útiles como j()j + 1) ≥ m()m + 1), y por lo tanto j ≥ m, entre otros.
En la mecánica no relativista, el tiempo es privilegiado como una variable independiente. Sin embargo, en 1945, L. I. Mandelshtam y I. E. Tamm derivaron un no relativista tiempo-energía incertidumbre relación, como sigue. Para un sistema cuántico en un estado no estacionario $↑$ y un observable B representado por un operador autónomo ${hat {B}}$ , la siguiente fórmula sostiene: ${displaystyle sigma _{E}{frac {sigma _{B}}{left|{frac {dlangle {hat {B}}rangle }{dt}}right|}}geq {frac {hbar }{2}},}$ Donde σ_E es la desviación estándar del operador de energía (Hamiltonian) en el estado $↑$ , σ_B representa la desviación estándar de B. Aunque el segundo factor en el lado izquierdo tiene dimensión de tiempo, es diferente del parámetro de tiempo que entra en la ecuación Schrödinger. Es una por vida del estado $↑$ con respecto al observable B: En otras palabras, esta es la intervalo de tiempo (Δ)t) después del cual el valor de expectativa $langle {hat {B}}rangle$ cambios apreciablemente.
Un significado informal y heurístico del principio es el siguiente: Un estado que sólo existe por un corto tiempo no puede tener una energía definida. Para tener una energía definida, la frecuencia del estado debe definirse con precisión, y esto requiere que el estado se cuelgue por muchos ciclos, el recíproco de la precisión necesaria. Por ejemplo, en la espectroscopia, estados excitados tienen una vida finita. Para el tiempo – principio de incertidumbre energética, no tienen una energía definida, y, cada vez que decaen, la energía que liberan es ligeramente diferente. La energía promedio del fotón saliente tiene un pico en la energía teórica del estado, pero la distribución tiene un ancho finito llamado el ancho de línea natural. Los estados rápidos tienen un ancho de línea amplio, mientras que los estados lentos tienen un ancho de línea estrecho.
El mismo efecto de ancho de línea también hace difícil especificar la masa restante de partículas inestables y rápidas en la física de partículas. Cuanto más rápido se desintegra la partícula (más corta su vida), menos seguro es su masa (más grande es el ancho de la partícula).
Para el número de electrones en un superconductor y la fase de su parámetro de orden Ginzburg-Landau ${displaystyle Delta N,Delta varphi geq 1.}$

Un contraejemplo

Supongamos que consideramos una partícula cuántica en un anillo, donde la función de onda depende de una variable angular $theta$ , que podemos tomar para mentir en el intervalo $[0,2pi]$ . Definir operadores de "posición" y "momentum" ${hat {A}}$ y ${hat {B}}$ por

{displaystyle {hat {A}}psi (theta)=theta psi (theta),quad theta in [0,2pi ],}

{displaystyle {hat {B}}psi =-ihbar {frac {dpsi }{dtheta }},}

{hat {B}}

{hat {A}}

theta

2pi

{displaystyle [{hat {A}},{hat {B}}]=ihbar }

Ahora $psi$ ser cualquiera de los eigentales de ${hat {B}}$ , que se dan por ${displaystyle psi (theta)=e^{2pi intheta }}$ . Estos estados son normalizables, a diferencia de los eigenstates del operador de impulso en la línea. También el operador ${hat {A}}$ está obligado, ya que $theta$ abarca un intervalo atado. Así, en el estado $psi$ , la incertidumbre de $B$ es cero y la incertidumbre de $A$ es finito, así que

{displaystyle sigma _{A}sigma _{B}=0.}

psi

{displaystyle {hat {B}}{hat {A}}}

theta

{hat {B}}

{displaystyle {hat {A}}{hat {B}}psi }

{displaystyle {hat {B}}{hat {A}}psi }

Para los operadores de posición e impulso habituales ${hat {X}}$ y $hat{P}$ en la línea real, no pueden ocurrir tales contraexamples. Mientras tanto $sigma _{x}$ y $sigma _{p}$ se definen en el estado $psi$ , el principio de incertidumbre Heisenberg sostiene, incluso si $psi$ no está en el dominio de ${displaystyle {hat {X}}{hat {P}}}$ o de ${displaystyle {hat {P}}{hat {X}}}$ .

Ejemplos

(Referencias)

Estados estacionarios del oscilador armónico cuántico

Considere un oscilador armónico cuántico unidimensional. Es posible expresar los operadores de posición y momento en términos de los operadores de creación y aniquilación:

{displaystyle {hat {x}}={sqrt {frac {hbar }{2momega }}}(a+a^{dagger })}

{displaystyle {hat {p}}=i{sqrt {frac {momega hbar }{2}}}(a^{dagger }-a).}

Usando las reglas estándar para los operadores de creación y aniquilación en los estados propios de energía,

{displaystyle a^{dagger }|nrangle ={sqrt {n+1}}|n+1rangle }

{displaystyle a|nrangle ={sqrt {n}}|n-1rangle}

{displaystyle sigma _{x}^{2}={frac {hbar }{momega }}left(n+{frac {1}{2}}right)}

{displaystyle sigma _{p}^{2}=hbar momega left(n+{frac {1}{2}}right),.}

{displaystyle sigma _{x}sigma _{p}=hbar left(n+{frac {1}{2}}right)geq {frac {hbar }{2}}.~}

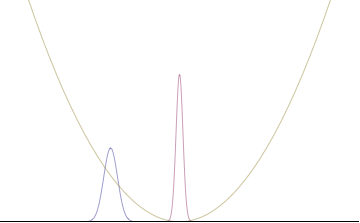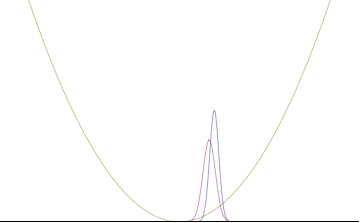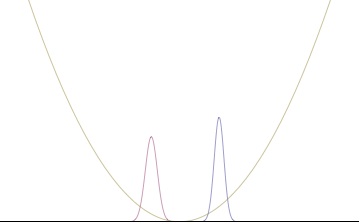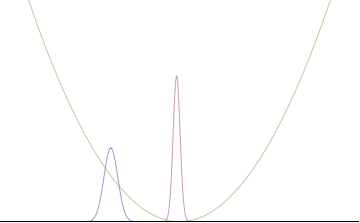
En particular, el límite de Kennard anterior está saturado para el estado fundamental $n =0$ , para el cual la densidad de probabilidad es simplemente la distribución normal.

Osciladores armónicos cuánticos con condición inicial gaussiana

Posición (azul) e impulso (rojo) densidades de probabilidad para una distribución Gausiana inicial. De arriba a abajo, las animaciones muestran los casos Ω=ω, Ω=2ω, y Ω=ω/2. Observe el intercambio entre los anchos de las distribuciones.

En un oscilador armónico cuántico de frecuencia angular característica ω, coloque un estado que esté compensado desde la parte inferior del potencial por algún desplazamiento x₀ como

{displaystyle psi (x)=left({frac {mOmega }{pi hbar }}right)^{1/4}exp {left(-{frac {mOmega (x-x_{0})^{2}}{2hbar }}right)},}

{displaystyle |Psi (x,t)|^{2}sim {mathcal {N}}left(x_{0}cos {(omega t)},{frac {hbar }{2mOmega }}left(cos ^{2}(omega t)+{frac {Omega ^{2}}{omega ^{2}}}sin ^{2}{(omega t)}right)right)}

{displaystyle |Phi (p,t)|^{2}sim {mathcal {N}}left(-mx_{0}omega sin(omega t),{frac {hbar mOmega }{2}}left(cos ^{2}{(omega t)}+{frac {omega ^{2}}{Omega ^{2}}}sin ^{2}{(omega t)}right)right),}

{mathcal {N}}(musigma ^{2})

{displaystyle {begin{aligned}sigma _{x}sigma _{p}&={frac {hbar }{2}}{sqrt {left(cos ^{2}{(omega t)}+{frac {Omega ^{2}}{omega ^{2}}}sin ^{2}{(omega t)}right)left(cos ^{2}{(omega t)}+{frac {omega ^{2}}{Omega ^{2}}}sin ^{2}{(omega t)}right)}}\&={frac {hbar }{4}}{sqrt {3+{frac {1}{2}}left({frac {Omega ^{2}}{omega ^{2}}}+{frac {omega ^{2}}{Omega ^{2}}}right)-left({frac {1}{2}}left({frac {Omega ^{2}}{omega ^{2}}}+{frac {omega ^{2}}{Omega ^{2}}}right)-1right)cos {(4omega t)}}}end{aligned}}}

De las relaciones

{displaystyle {frac {Omega ^{2}}{omega ^{2}}}+{frac {omega ^{2}}{Omega ^{2}}}geq 2,quad |cos(4omega t)|leq 1,}

⋅

{displaystyle sigma _{x}sigma _{p}geq {frac {hbar }{4}}{sqrt {3+{frac {1}{2}}left({frac {Omega ^{2}}{omega ^{2}}}+{frac {omega ^{2}}{Omega ^{2}}}right)-left({frac {1}{2}}left({frac {Omega ^{2}}{omega ^{2}}}+{frac {omega ^{2}}{Omega ^{2}}}right)-1right)}}={frac {hbar }{2}}.}

Estados coherentes

Un estado coherente es un estado propio derecho del operador de aniquilación,

{displaystyle {hat {a}}|alpha rangle =alpha |alpha rangle}

{displaystyle |alpha rangle =e^{-{|alpha |^{2} over 2}}sum _{n=0}^{infty }{alpha ^{n} over {sqrt {n!}}}|nrangle }

En la imagen donde el estado coherente es una partícula masiva en un oscilador armónico cuántico, los operadores de posición y momento pueden expresarse en términos de los operadores de aniquilación en las mismas fórmulas anteriores y usarse para calcular las varianzas,

{displaystyle sigma _{x}^{2}={frac {hbar }{2momega }},}

{displaystyle sigma _{p}^{2}={frac {hbar momega }{2}}.}

{displaystyle sigma _{x}sigma _{p}={sqrt {frac {hbar }{2momega }}},{sqrt {frac {hbar momega }{2}}}={frac {hbar }{2}}.}

{textstyle {sqrt {hbar /2}}}

Partícula en una caja

Considere una partícula en una caja de longitud unidimensional $L$ . Las funciones eigen en la posición y el espacio de impulso son

<math alttext="{displaystyle psi _{n}(x,t)={begin{cases}Asin(k_{n}x)mathrm {e} ^{-mathrm {i} omega _{n}t},&0<x↑ ↑ n()x,t)={}Apecado⁡ ⁡ ()knx)e− − i⋅ ⋅ nt,0.x.L,0,de lo contrario,{displaystyle psi _{n}(x,t)={begin{cases}Asin(k_{n}x)mathrm {e} ^{-mathrm {i} omega _{n}t}, ventaja0 significa que,, quedamos juntos.<img alt="{displaystyle psi _{n}(x,t)={begin{cases}Asin(k_{n}x)mathrm {e} ^{-mathrm {i} omega _{n}t},&0<x

{displaystyle varphi _{n}(p,t)={sqrt {frac {pi L}{hbar }}},,{frac {nleft(1-(-1)^{n}e^{-ikL}right)e^{-iomega _{n}t}}{pi ^{2}n^{2}-k^{2}L^{2}}},}

{textstyle omega _{n}={frac {pi ^{2}hbar n^{2}}{8L^{2}m}}}

p=hbar k

x

p

{displaystyle sigma _{x}^{2}={frac {L^{2}}{12}}left(1-{frac {6}{n^{2}pi ^{2}}}right)}

{displaystyle sigma _{p}^{2}=left({frac {hbar npi }{L}}right)^{2}.}

Por lo tanto, el producto de las desviaciones estándar es

{displaystyle sigma _{x}sigma _{p}={frac {hbar }{2}}{sqrt {{frac {n^{2}pi ^{2}}{3}}-2}}.}

{displaystyle n=1,,2,,3,,ldots }

{textstyle {sqrt {{frac {n^{2}pi ^{2}}{3}}-2}}}

n=1

{frac {hbar }{2}}.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">σ σ xσ σ p=▪ ▪ 2π π 23− − 2.. 0,5668▪ ▪ ■▪ ▪ 2.{displaystyle sigma _{x}sigma - ¿Qué? {hbar }{sqrt {fnMic {fnMic} {fnh} {fnh} {fn}} {fn} {fnfnK} {fnfnfnfnf}} {fnf}}} {fnfn\fnfnfnfnfnfnhbar}}}}}}}}fnfnfnfnfnfnfnfn\fnfnfnfnfnfnfnfnfn\fnfn\\fn\fn\fnfn\fnfn\fnfnfnfn}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\fn ^{2}{3}-2}approx 0,568hbar } {2}}.{frac {hbar }{2}}.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/edd3a568ee8802277749daa4043f19f2c4aab3e4" style="vertical-align: -2.171ex; width:35.268ex; height:6.176ex;"/>

Impulso constante

Posición de la densidad de probabilidad espacial de un estado inicialmente Gaussiano que se mueve con un impulso mínimo incierto y constante en el espacio libre

Suponga que una partícula inicialmente tiene una función de onda espacial de momento descrita por una distribución normal alrededor de un momento constante p₀ de acuerdo con

{displaystyle varphi (p)=left({frac {x_{0}}{hbar {sqrt {pi }}}}right)^{1/2}exp left({frac {-x_{0}^{2}(p-p_{0})^{2}}{2hbar ^{2}}}right),}

{textstyle x_{0}={sqrt {hbar /momega _{0}}}}

0}" xmlns="http://www.w3.org/1998/Math/MathML">⋅ ⋅ 0■0{displaystyle omega ¿Qué?0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b1760f9faf283234d7341a658b0431cde4510c66" style="vertical-align: -0.671ex; width:6.761ex; height:2.509ex;"/>

{displaystyle Phi (p,t)=left({frac {x_{0}}{hbar {sqrt {pi }}}}right)^{1/2}exp left({frac {-x_{0}^{2}(p-p_{0})^{2}}{2hbar ^{2}}}-{frac {ip^{2}t}{2mhbar }}right),}

{displaystyle Psi (x,t)=left({frac {1}{x_{0}{sqrt {pi }}}}right)^{1/2}{frac {e^{-x_{0}^{2}p_{0}^{2}/2hbar ^{2}}}{sqrt {1+iomega _{0}t}}},exp left(-{frac {(x-ix_{0}^{2}p_{0}/hbar)^{2}}{2x_{0}^{2}(1+iomega _{0}t)}}right).}

Desde $langle p(t)rangle =p_{0}$ y ${displaystyle sigma _{p}(t)=hbar /({sqrt {2}}x_{0})}$ , esto se puede interpretar como una partícula que se mueve junto con el impulso constante a la precisión arbitrariamente alta. Por otro lado, la desviación estándar de la posición es

{displaystyle sigma _{x}={frac {x_{0}}{sqrt {2}}}{sqrt {1+omega _{0}^{2}t^{2}}}}

{displaystyle sigma _{x}(t)sigma _{p}(t)={frac {hbar }{2}}{sqrt {1+omega _{0}^{2}t^{2}}}}

Relaciones de incertidumbre adicional

Errores sistemáticos y estadísticos

Las desigualdades anteriores se centran en la Imprecisión estadística de los observables cuantificados por la desviación estándar $sigma$ . La versión original de Heisenberg, sin embargo, estaba tratando con la error sistemático, una perturbación del sistema cuántico producido por el aparato de medición, es decir, un efecto observador.

Si lo dejamos ${displaystyle varepsilon _{A}}$ representar el error (es decir, inexactitud) de una medición de un observable A y $eta _{B}$ la perturbación producida en una medición posterior de la variable conjugada B por la anterior medición de A, entonces la desigualdad propuesta por Ozawa —que abarca tanto errores sistemáticos como estadísticos— sostiene:

${displaystyle varepsilon _{A},eta _{B}+varepsilon _{A},sigma _{B}+sigma _{A},eta _{B},geq ,{frac {1}{2}},left|{Bigl langle }{bigl [}{hat {A}},{hat {B}}{bigr ]}{Bigr rangle }right|}$

El principio de incertidumbre de Heisenberg, como se describió originalmente en la formulación de 1927, menciona solo el primer término de la desigualdad de Ozawa, con respecto al error sistemático. Usando la notación anterior para describir el efecto error/perturbación de medidas secuenciales (primero A, luego B), podría escribirse como

${displaystyle varepsilon _{A},eta _{B},geq ,{frac {1}{2}},left|{Bigl langle }{bigl [}{hat {A}},{hat {B}}{bigr ]}{Bigr rangle }right|}$

La derivación formal de la relación Heisenberg es posible pero lejos de intuitiva. Era no propuesto por Heisenberg, pero formulado de manera matemáticamente coherente sólo en los últimos años. Además, cabe destacar que la formulación Heisenberg no tiene en cuenta los errores estadísticos intrínsecos $sigma _{A}$ y $sigma _{B}$ . Hay cada vez más pruebas experimentales de que la incertidumbre cuántica total no puede describirse sólo por el término Heisenberg, sino que requiere la presencia de los tres términos de la desigualdad Ozawa.

Usando el mismo formalismo, también es posible introducir el otro tipo de situación física, a menudo confundida con la anterior, a saber, el caso de medidas simultáneas (A y B al mismo tiempo):

${displaystyle varepsilon _{A},varepsilon _{B},geq ,{frac {1}{2}},left|{Bigl langle }{bigl [}{hat {A}},{hat {B}}{bigr ]}{Bigr rangle }right|}$

Las dos medidas simultáneas en A y B son necesariamente poco nítidas o débiles.

También es posible derivar una relación de incertidumbre que, como la de Ozawa, combina los componentes de error estadístico y sistemático, pero mantiene una forma muy cercana a la desigualdad original de Heisenberg. Al agregar Robertson

${displaystyle sigma _{A},sigma _{B},geq ,{frac {1}{2}},left|{Bigl langle }{bigl [}{hat {A}},{hat {B}}{bigr ]}{Bigr rangle }right|}$

y las relaciones de Ozawa obtenemos

{displaystyle varepsilon _{A}eta _{B}+varepsilon _{A},sigma _{B}+sigma _{A},eta _{B}+sigma _{A}sigma _{B}geq left|{Bigl langle }{bigl [}{hat {A}},{hat {B}}{bigr ]}{Bigr rangle }right|.}

{displaystyle (varepsilon _{A}+sigma _{A}),(eta _{B}+sigma _{B}),geq ,left|{Bigl langle }{bigl [}{hat {A}},{hat {B}}{bigr ]}{Bigr rangle }right|.}

{displaystyle {bar {varepsilon }}_{A},equiv ,(varepsilon _{A}+sigma _{A})}

inexactitudA

{displaystyle {bar {eta }}_{B},equiv ,(eta _{B}+sigma _{B})}

fluctuación resultanteBerrores sistemáticos y estadísticos

${displaystyle {bar {varepsilon }}_{A},{bar {eta }}_{B},geq ,left|{Bigl langle }{bigl [}{hat {A}},{hat {B}}{bigr ]}{Bigr rangle }right|}$

Principio de incertidumbre entrópica cuántica

Para muchas distribuciones, la desviación estándar no es una forma particularmente natural de cuantificar la estructura. Por ejemplo, las relaciones de incertidumbre en las que uno de los observables es un ángulo tienen poco significado físico para fluctuaciones mayores de un período. Otros ejemplos incluyen distribuciones altamente bimodales o distribuciones unimodales con varianza divergente.

Una solución que supera estos problemas es una incertidumbre basada en la incertidumbre entrópica en lugar del producto de varianzas. Mientras formulaba la interpretación de muchos mundos de la mecánica cuántica en 1957, Hugh Everett III conjeturó una mayor extensión del principio de incertidumbre basado en la certeza entrópica. Esta conjetura, también estudiada por Hirschman y probada en 1975 por Beckner y por Iwo Bialynicki-Birula y Jerzy Mycielski es que, para dos pares de transformadas de Fourier normalizados y adimensionales $f (a)$ y $g (b)$ donde

{displaystyle f(a)=int _{-infty }^{infty }g(b) e^{2pi iab},db}

{displaystyle ,,,g(b)=int _{-infty }^{infty }f(a) e^{-2pi iab},da}

las entropías de información de Shannon

{displaystyle H_{a}=int _{-infty }^{infty }f(a)log(f(a)),da,}

{displaystyle H_{b}=int _{-infty }^{infty }g(b)log(g(b)),db}

${displaystyle H_{a}+H_{b}geq log(e/2)}$

donde los logaritmos pueden estar en cualquier base.

Las funciones de distribución de probabilidad asociadas con la función de onda de posición $ψ (x)$ y la función de onda de impulso $φ (x)$ tienen dimensiones de longitud y momento inversos respectivamente, pero las entropías pueden volverse adimensionales por

{displaystyle H_{x}=-int |psi (x)|^{2}ln left(x_{0},|psi (x)|^{2}right)dx=-leftlangle ln left(x_{0},left|psi (x)right|^{2}right)rightrangle }

{displaystyle H_{p}=-int |varphi (p)|^{2}ln(p_{0},|varphi (p)|^{2}),dp=-leftlangle ln(p_{0}left|varphi (p)right|^{2})rightrangle }

x 0

p 0

↑ () x)

φ () p)

${displaystyle H_{x}+H_{p}geq log left({frac {e,h}{2,x_{0},p_{0}}}right)}$

donde $h$ es la constante de Planck.

Dependiendo de la elección de uno de $x 0 p 0$ producto, la expresión se puede escribir de muchas maneras. Si $x 0 p 0$ se elige para ser $h$ , luego

{displaystyle H_{x}+H_{p}geq log left({frac {e}{2}}right)}

Si, en cambio, $x 0 p 0$ se elige para que sea $ħ$ , luego

{displaystyle H_{x}+H_{p}geq log(e,pi)}

Si $x 0$ y $p 0$ se eligen para ser la unidad en cualquier sistema de unidades que se esté utilizando, entonces

{displaystyle H_{x}+H_{p}geq log left({frac {e,h}{2}}right)}

h

El principio de incertidumbre entrópica cuántica es más restrictivo que el principio de incertidumbre de Heisenberg. De las desigualdades logarítmicas inversas de Sobolev

{displaystyle H_{x}leq {frac {1}{2}}log(2epi sigma _{x}^{2}/x_{0}^{2})~,}

{displaystyle H_{p}leq {frac {1}{2}}log(2epi sigma _{p}^{2}/p_{0}^{2})~,}

más fuerte que el basado en desviaciones estándar

{displaystyle sigma _{x}sigma _{p}geq {frac {hbar }{2}}exp left(H_{x}+H_{p}-log left({frac {e,h}{2,x_{0},p_{0}}}right)right)geq {frac {hbar }{2}}~.}

En otras palabras, el principio de incertidumbre de Heisenberg es una consecuencia del principio de incertidumbre entrópico cuántico, pero no al revés. Algunas observaciones sobre estas desigualdades. Primero, la elección de la base e es una cuestión de convención popular en física. El logaritmo puede estar alternativamente en cualquier base, siempre que sea consistente en ambos lados de la desigualdad. En segundo lugar, recuerde que se ha utilizado la entropía de Shannon, no la entropía cuántica de von Neumann. Finalmente, la distribución normal satura la desigualdad, y es la única distribución con esta propiedad, porque es la distribución de probabilidad de máxima entropía entre aquellas con varianza fija (cf. aquí para la prueba).

Incierto entropico de la distribución normal

Demostramos este método en el estado de la QHO, que como se discutió anteriormente satura la incertidumbre habitual basada en desviaciones estándar. La escala de longitud se puede fijar a lo que sea conveniente, por lo que asignamos

{displaystyle x_{0}={sqrt {frac {hbar }{2momega }}}}

{displaystyle {begin{aligned}psi (x)&=left({frac {momega }{pi hbar }}right)^{1/4}exp {left(-{frac {momega x^{2}}{2hbar }}right)}\&=left({frac {1}{2pi x_{0}^{2}}}right)^{1/4}exp {left(-{frac {x^{2}}{4x_{0}^{2}}}right)}end{aligned}}}

La distribución de probabilidad es la distribución normal

{displaystyle |psi (x)|^{2}={frac {1}{x_{0}{sqrt {2pi }}}}exp {left(-{frac {x^{2}}{2x_{0}^{2}}}right)}}

con Shannon entropy

{displaystyle {begin{aligned}H_{x}&=-int |psi (x)|^{2}ln(|psi (x)|^{2}cdot x_{0}),dx\&=-{frac {1}{x_{0}{sqrt {2pi }}}}int _{-infty }^{infty }exp {left(-{frac {x^{2}}{2x_{0}^{2}}}right)}ln left[{frac {1}{sqrt {2pi }}}exp {left(-{frac {x^{2}}{2x_{0}^{2}}}right)}right],dx\&={frac {1}{sqrt {2pi }}}int _{-infty }^{infty }exp {left(-{frac {u^{2}}{2}}right)}left[ln({sqrt {2pi }})+{frac {u^{2}}{2}}right],du\&=ln({sqrt {2pi }})+{frac {1}{2}}.end{aligned}}}

Un cálculo completamente análogo procede para la distribución del impulso. Elegir un impulso estándar ${displaystyle p_{0}=hbar /x_{0}}$ :

{displaystyle varphi (p)=left({frac {2x_{0}^{2}}{pi hbar ^{2}}}right)^{1/4}exp {left(-{frac {x_{0}^{2}p^{2}}{hbar ^{2}}}right)}}

{displaystyle |varphi (p)|^{2}={sqrt {frac {2x_{0}^{2}}{pi hbar ^{2}}}}exp {left(-{frac {2x_{0}^{2}p^{2}}{hbar ^{2}}}right)}}

{displaystyle {begin{aligned}H_{p}&=-int |varphi (p)|^{2}ln(|varphi (p)|^{2}cdot hbar /x_{0}),dp\&=-{sqrt {frac {2x_{0}^{2}}{pi hbar ^{2}}}}int _{-infty }^{infty }exp {left(-{frac {2x_{0}^{2}p^{2}}{hbar ^{2}}}right)}ln left[{sqrt {frac {2}{pi }}}exp {left(-{frac {2x_{0}^{2}p^{2}}{hbar ^{2}}}right)}right],dp\&={sqrt {frac {2}{pi }}}int _{-infty }^{infty }exp {left(-2v^{2}right)}left[ln left({sqrt {frac {pi }{2}}}right)+2v^{2}right],dv\&=ln left({sqrt {frac {pi }{2}}}right)+{frac {1}{2}}.end{aligned}}}

Por lo tanto, la incertidumbre entropica es el valor límite

{displaystyle {begin{aligned}H_{x}+H_{p}&=ln({sqrt {2pi }})+{frac {1}{2}}+ln left({sqrt {frac {pi }{2}}}right)+{frac {1}{2}}\&=1+ln pi =ln(epi).end{aligned}}}

Un aparato de medición tendrá una resolución finita establecida por la discretización de sus posibles salidas en contenedores, con la probabilidad de estar dentro de uno de los contenedores dados por la regla de Born. Consideraremos la situación experimental más común, en la que los contenedores tienen un tamaño uniforme. Sea δx una medida de la resolución espacial. Tomamos el contenedor cero para que esté centrado cerca del origen, posiblemente con algún pequeño desplazamiento constante c. La probabilidad de estar dentro del j-ésimo intervalo de ancho δx es

{displaystyle operatorname {P} [x_{j}]=int _{(j-1/2)delta x-c}^{(j+1/2)delta x-c}|psi (x)|^{2},dx}

Para dar cuenta de esta discretización, podemos definir la entropía de Shannon de la función de onda para un aparato de medición dado como

{displaystyle H_{x}=-sum _{j=-infty }^{infty }operatorname {P} [x_{j}]ln operatorname {P} [x_{j}].}

Según la definición anterior, la relación de incertidumbre entrópica es

ln left({frac {e}{2}}right)-ln left({frac {delta xdelta p}{h}}right).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Hx+Hp■In⁡ ⁡ ()e2)− − In⁡ ⁡ ()δ δ xδ δ ph).{displaystyle H_{x}+H_{p}ln left({frac {e}{2}right)-ln left({frac {delta xdelta p}{h}right). }ln left({frac {e}{2}}right)-ln left({frac {delta xdelta p}{h}}right).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/246dbdfcb1fe677ba62756deee9af8eaaf6faa09" style="vertical-align: -2.505ex; width:33.027ex; height:6.176ex;"/>

Aquí notamos que $δx δp / h$ es un espacio de fase infinitesimal típico volumen utilizado en el cálculo de una función de partición. La desigualdad también es estricta y no saturada. Los esfuerzos para mejorar este límite son un área activa de investigación.

Ejemplo de distribución normal

Demostramos este método primero en el estado de la QHO, que como se discutió anteriormente satura la incertidumbre habitual basada en desviaciones estándar.

{displaystyle psi (x)=left({frac {momega }{pi hbar }}right)^{1/4}exp {left(-{frac {momega x^{2}}{2hbar }}right)}}

La probabilidad de mentir dentro de uno de estos contenedores se puede expresar en términos de la función de error.

{displaystyle {begin{aligned}operatorname {P} [x_{j}]&={sqrt {frac {momega }{pi hbar }}}int _{(j-1/2)delta x}^{(j+1/2)delta x}exp left(-{frac {momega x^{2}}{hbar }}right),dx\&={sqrt {frac {1}{pi }}}int _{(j-1/2)delta x{sqrt {momega /hbar }}}^{(j+1/2)delta x{sqrt {momega /hbar }}}e^{u^{2}},du\&={frac {1}{2}}left[operatorname {erf} left(left(j+{frac {1}{2}}right)delta xcdot {sqrt {frac {momega }{hbar }}}right)-operatorname {erf} left(left(j-{frac {1}{2}}right)delta xcdot {sqrt {frac {momega }{hbar }}}right)right]end{aligned}}}

Las probabilidades de impulso son completamente análogas.

{displaystyle operatorname {P} [p_{j}]={frac {1}{2}}left[operatorname {erf} left(left(j+{frac {1}{2}}right)delta pcdot {frac {1}{sqrt {hbar momega }}}right)-operatorname {erf} left(left(j-{frac {1}{2}}right)delta xcdot {frac {1}{sqrt {hbar momega }}}right)right]}

Para la simplicidad, estableceremos las resoluciones

{displaystyle delta x={sqrt {frac {h}{momega }}}}

{displaystyle delta p={sqrt {hmomega }}}

para que las probabilidades se reduzcan

{displaystyle operatorname {P} [x_{j}]=operatorname {P} [p_{j}]={frac {1}{2}}left[operatorname {erf} left(left(j+{frac {1}{2}}right){sqrt {2pi }}right)-operatorname {erf} left(left(j-{frac {1}{2}}right){sqrt {2pi }}right)right]}

La entropía Shannon se puede evaluar numéricamente.

{displaystyle {begin{aligned}H_{x}=H_{p}&=-sum _{j=-infty }^{infty }operatorname {P} [x_{j}]ln operatorname {P} [x_{j}]\&=-sum _{j=-infty }^{infty }{frac {1}{2}}left[operatorname {erf} left(left(j+{frac {1}{2}}right){sqrt {2pi }}right)-operatorname {erf} left(left(j-{frac {1}{2}}right){sqrt {2pi }}right)right]ln {frac {1}{2}}left[operatorname {erf} left(left(j+{frac {1}{2}}right){sqrt {2pi }}right)-operatorname {erf} left(left(j-{frac {1}{2}}right){sqrt {2pi }}right)right]\&approx 0.3226end{aligned}}}

La incertidumbre entropica es más grande que el valor límite.

ln left({frac {e}{2}}right)-ln 1approx 0.3069}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Hx+Hp.. 0,3226+0,3226=0.6452■In⁡ ⁡ ()e2)− − In⁡ ⁡ 1.. 0.3069{displaystyle H_{x}+H_{p}approx 0.3226+0.3226=0.6452 confianzaln left({frac {e}{2}right)-ln 1approx 0.3069}ln left({frac {e}{2}}right)-ln 1approx 0.3069}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/31a27b561bd82e9fd02f01af30d47953aecbaf9a" style="vertical-align: -1.838ex; width:63.048ex; height:4.843ex;"/>

Tenga en cuenta que a pesar de estar en el caso óptimo, la desigualdad no está saturada.

Ejemplo de función Sinc

Un ejemplo de una distribución unimodal con varianza infinita es la función sinc. Si la función de onda es la distribución uniforme normalizada correctamente,

aend{cases}}}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">↑ ↑ ()x)={}1/2aparaSilencioxSilencio≤ ≤ a,0paraSilencioxSilencio■a{displaystyle psi (x)={begin{cases}{1}/{sqrt {2a} limit{text{for }}Principe a,[8pt]0 ventaja{text{for }}Principio aend{cases}}}}}}aend{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6252d65b527d2b4bf3a708c339d7907976267c45" style="vertical-align: -3.338ex; width:30.316ex; height:7.843ex;"/>

entonces Fourier transforma es la función sinc,

{displaystyle varphi (p)={sqrt {frac {a}{pi hbar }}}cdot operatorname {sinc} left({frac {ap}{hbar }}right)}

que produce una varianza de impulso infinita a pesar de tener una forma centralizada. La incertidumbre entropica, por otro lado, es finita. Supongamos para la simplicidad que la resolución espacial es sólo una medición de dos-bines, δx=a, y que la resolución del impulso es δp=h/a.

Partitioning the uniform spatial distribution into two equal bins is straightforward. Hemos fijado el offset c= 1/2 para que los dos contenedores abarquen la distribución.

{displaystyle operatorname {P} [x_{0}]=int _{-a}^{0}{frac {1}{2a}},dx={frac {1}{2}}}

{displaystyle operatorname {P} [x_{1}]=int _{0}^{a}{frac {1}{2a}},dx={frac {1}{2}}}

{displaystyle H_{x}=-sum _{j=0}^{1}operatorname {P} [x_{j}]ln operatorname {P} [x_{j}]=-{frac {1}{2}}ln {frac {1}{2}}-{frac {1}{2}}ln {frac {1}{2}}=ln 2}

Los cubos para el impulso deben cubrir toda la línea real. Como se hizo con la distribución espacial, podríamos aplicar un offset. Resulta, sin embargo, que la entropía Shannon es minimizada cuando el bin cero para el impulso se centra en el origen. (Se alienta al lector a intentar agregar un offset.) La probabilidad de mentir dentro de un contenedor de impulso arbitrario se puede expresar en términos de la integral sine.

{displaystyle {begin{aligned}operatorname {P} [p_{j}]&={frac {a}{pi hbar }}int _{(j-1/2)delta p}^{(j+1/2)delta p}operatorname {sinc} ^{2}left({frac {ap}{hbar }}right),dp\&={frac {1}{pi }}int _{2pi (j-1/2)}^{2pi (j+1/2)}operatorname {sinc} ^{2}(u),du\&={frac {1}{pi }}left[operatorname {Si} ((4j+2)pi)-operatorname {Si} ((4j-2)pi)right]end{aligned}}}

La entropía Shannon se puede evaluar numéricamente.

{displaystyle H_{p}=-sum _{j=-infty }^{infty }operatorname {P} [p_{j}]ln operatorname {P} [p_{j}]=-operatorname {P} [p_{0}]ln operatorname {P} [p_{0}]-2cdot sum _{j=1}^{infty }operatorname {P} [p_{j}]ln operatorname {P} [p_{j}]approx 0.53}

La incertidumbre entropica es más grande que el valor límite.

ln left({frac {e}{2}}right)-ln 1approx 0.31}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Hx+Hp.. 0.69+0,53=1.22■In⁡ ⁡ ()e2)− − In⁡ ⁡ 1.. 0.31{displaystyle H_{x}+H_{p}approx 0,69+0.53=1.22 tituladaln left({frac {e}{2}right)-ln 1approx 0,31}ln left({frac {e}{2}}right)-ln 1approx 0.31}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/979d41a023ebc6d3eae49cd97e6af99f96194743" style="vertical-align: -1.838ex; width:53.748ex; height:4.843ex;"/>

Relación de incertidumbre con tres componentes de momento angular

Para una partícula de spin- $j$ la siguiente relación de incertidumbre

{displaystyle sigma _{J_{x}}^{2}+sigma _{J_{y}}^{2}+sigma _{J_{z}}^{2}geq j,}

{displaystyle J_{l}}

{displaystyle langle J_{x}^{2}+J_{y}^{2}+J_{z}^{2}rangle =j(j+1),}

{displaystyle langle J_{x}rangle ^{2}+langle J_{y}rangle ^{2}+langle J_{z}rangle ^{2}leq j.}

{displaystyle sigma _{J_{x}}^{2}+sigma _{J_{y}}^{2}+F_{Q}[varrhoJ_{z}]/4geq j,}

{displaystyle F_{Q}[varrhoJ_{z}]}

Análisis armónico

En el contexto del análisis armónico, una rama de las matemáticas, el principio de incertidumbre implica que no se puede localizar al mismo tiempo el valor de una función y su transformada de Fourier. A saber, se cumple la siguiente desigualdad,

{displaystyle left(int _{-infty }^{infty }x^{2}|f(x)|^{2},dxright)left(int _{-infty }^{infty }xi ^{2}|{hat {f}}(xi)|^{2},dxi right)geq {frac {|f|_{2}^{4}}{16pi ^{2}}}.}

Más desigualdades de incertidumbre matemática, incluida la incertidumbre entrópica anterior, se dan entre una función $f$ y su transformada de Fourier ƒ̂:

{displaystyle H_{x}+H_{xi }geq log(e/2)}

Procesamiento de señales

En el contexto del procesamiento de señales y, en particular, del análisis de tiempo-frecuencia, los principios de incertidumbre se conocen como el límite de Gabor, en honor a Dennis Gabor, o a veces el límite de Heisenberg-Gabor. El resultado básico, que se deriva del "teorema de Benedictis", a continuación, es que una función no puede estar limitada en el tiempo y en la banda (una función y su transformada de Fourier no pueden tener un dominio acotado)—ver banda limitada versus tiempo limitado. Por lo tanto

{displaystyle sigma _{t}cdot sigma _{f}geq {frac {1}{4pi }}approx 0.08{text{ cycles}},}

sigma _{t}

sigma _{f}

Dicho de otro modo, "uno no puede localizar de forma precisa una señal simultáneamente (función $f$ ) tanto en el dominio del tiempo como en el dominio de frecuencia ( $ƒ̂$ , su transformada de Fourier)".

Cuando se aplica a los filtros, el resultado implica que no se puede lograr una resolución temporal alta y una resolución de frecuencia al mismo tiempo; un ejemplo concreto son los problemas de resolución de la transformada de Fourier de tiempo corto: si se usa una ventana ancha, se logra una buena resolución de frecuencia a costa de la resolución temporal, mientras que una ventana estrecha tiene la contrapartida.

Los teoremas alternativos brindan resultados cuantitativos más precisos y, en el análisis de tiempo-frecuencia, en lugar de interpretar los dominios de tiempo y frecuencia (unidimensionales) por separado, uno interpreta el límite como un límite inferior en el soporte de una función en el plano (bidimensional) de tiempo-frecuencia. En la práctica, el límite de Gabor limita la resolución de tiempo-frecuencia simultánea que se puede lograr sin interferencia; es posible lograr una resolución más alta, pero a costa de que diferentes componentes de la señal interfieran entre sí.

Como resultado, para analizar señales en las que los transitorios son importantes, a menudo se usa la transformada wavelet en lugar de Fourier.

Transformada discreta de Fourier

Vamos ${displaystyle left{mathbf {x_{n}} right}:=x_{0},x_{1},ldotsx_{N-1}}$ ser una secuencia de N números complejos y ${displaystyle left{mathbf {X_{k}} right}:=X_{0},X_{1},ldotsX_{N-1},}$ su discreta transformación Fourier.

Denote by $|x|_{0}$ el número de elementos no cero en la secuencia del tiempo $x_{0},x_{1},ldotsx_{N-1}$ y por $|X|_{0}$ el número de elementos no cero en la secuencia de frecuencias $X_{0},X_{1},ldotsX_{N-1}$ . Entonces,

{displaystyle |x|_{0}cdot |X|_{0}geq N.}

Esta desigualdad es pronunciada, y se logra la igualdad cuando x o X es una masa de Dirac, o más generalmente cuando x es un múltiplo distinto de cero de un peine de Dirac apoyado en un subgrupo de los enteros módulo N (en cuyo caso X es también un peine de Dirac apoyado en un subgrupo complementario, y viceversa).

Más generalmente, si T y W son subconjuntos de los enteros modulo N, vamos ${displaystyle L_{T},R_{W}:ell ^{2}(mathbb {Z} /Nmathbb {N})to ell ^{2}(mathbb {Z} /Nmathbb {N})}$ denota el operador de limitación de tiempo y operadores de limitación de bandas, respectivamente. Entonces...

{displaystyle |L_{T}R_{W}|^{2}leq {frac {|T||W|}{|G|}}}

{displaystyle ell ^{2}(mathbb {Z} /Nmathbb {Z})}

Cuando N es un número primo, se cumple una desigualdad más fuerte:

{displaystyle |x|_{0}+|X|_{0}geq N+1.}

Teorema de Benedictis

El teorema de Amrein–Berthier y Benedicks dice intuitivamente que el conjunto de puntos donde $f$ es distinto de cero y el conjunto de puntos donde $ƒ̂$ es distinto de cero no puede ser pequeño.

Específicamente, es imposible para una función $f$ en $L 2 (R)$ y su transformada de Fourier $ƒ̂$ para que ambos sean compatibles con conjuntos finitos de Lebesgue medida. Una versión más cuantitativa es

{displaystyle |f|_{L^{2}(mathbf {R} ^{d})}leq Ce^{C|S||Sigma |}{bigl (}|f|_{L^{2}(S^{c})}+|{hat {f}}|_{L^{2}(Sigma ^{c})}{bigr)}~.}

Uno espera que el factor $Ce C|S||Σ|$ pueda ser reemplazado por $Ce C (| S ||Σ|) 1/ d$ , que solo se conoce si $S$ o $Σ$ es convexo.

Principio de incertidumbre de Hardy

El matemático G. H. Hardy formuló el siguiente principio de incertidumbre: no es posible $f$ y $.$ para ser "muy rápidamente disminuyendo". Específicamente, si $f$ dentro $L^2(mathbb{R})$ es tal que

{displaystyle |f(x)|leq C(1+|x|)^{N}e^{-api x^{2}}}

{displaystyle |{hat {f}}(xi)|leq C(1+|xi |)^{N}e^{-bpi xi ^{2}}}

0,N}" xmlns="http://www.w3.org/1998/Math/MathML">C■0,N{displaystyle C confiar0,N}0,N" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3bd15c1f755778480125f8aee37cd9b1f91e4178" style="vertical-align: -0.671ex; width:9.125ex; height:2.509ex;"/>

entonces, si $ab > 1, f = 0$ , mientras que si $ab = 1$ , entonces existe un polinomio $P$ de grado $\leq N$ tal que

{displaystyle f(x)=P(x)e^{-api x^{2}}.}

This was later improved as follows: si ${displaystyle fin L^{2}(mathbb {R} ^{d})}$ es tal que

<math alttext="{displaystyle int _{mathbb {R} ^{d}}int _{mathbb {R} ^{d}}|f(x)||{hat {f}}(xi)|{frac {e^{pi |langle x,xi rangle |}}{(1+|x|+|xi |)^{N}}},dx,dxi ∫ ∫ Rd∫ ∫ RdSilenciof()x)SilencioSilenciof^ ^ ().. )Silencioeπ π Silencio.. x,.. .. Silencio()1+SilencioxSilencio+Silencio.. Silencio)Ndxd.. .+JUEGO JUEGO ,{displaystyle int _{mathbb {R} ^{d}int _{mathbb {R} } ↑f(x) La vida eterna {hat {hat} {xi) La vida eterna {frac {e^{pi langle x,xirangle ¦}{(1+ vidas subsistentexi)} {N}},dx,dxi,dxi]<img alt="{displaystyle int _{mathbb {R} ^{d}}int _{mathbb {R} ^{d}}|f(x)||{hat {f}}(xi)|{frac {e^{pi |langle x,xi rangle |}}{(1+|x|+|xi |)^{N}}},dx,dxi

{displaystyle f(x)=P(x)e^{-pi langle Ax,xrangle }~,}

P

() N - d)/2

A

d \times d

Este resultado fue declarado en las obras completas de Beurling sin pruebas y probado en Hörmander (el caso $d=1,N=0$ ) y Bonami, Demange, y Jaming para el caso general. Tenga en cuenta que la versión de Hörmander-Beurling implica el caso $ab ■ 1$ en Hardy's Teorema mientras la versión de Bonami–Demange–Jaming cubre la fuerza total del Teorema de Hardy. Una prueba diferente del teorema de Beurling basado en el teorema de Liouville apareció en ref.

Una descripción completa del caso $ab < 1$ así como la siguiente extensión a las distribuciones de clase de Schwartz aparece en la ref.

Theorem— Si una distribución templada $fin {mathcal {S}}'(mathbb {R} ^{d})$ es tal que

{displaystyle e^{pi |x|^{2}}fin {mathcal {S}}'(mathbb {R} ^{d})}

{displaystyle e^{pi |xi |^{2}}{hat {f}}in {mathcal {S}}'(mathbb {R} ^{d})~,}

entonces

{displaystyle f(x)=P(x)e^{-pi langle Ax,xrangle }~,}

para algunos polinomios convenientes

P

y verdadera matriz definida positiva

A

tipo

d \times d

Historia

Werner Heisenberg formuló el principio de incertidumbre en el instituto Niels Bohr de Copenhague, mientras trabajaba en los fundamentos matemáticos de la mecánica cuántica.

Werner Heisenberg y Niels Bohr

En 1925, siguiendo el trabajo pionero con Hendrik Kramers, Heisenberg desarrolló la mecánica matricial, que reemplazó la antigua teoría cuántica ad hoc con la mecánica cuántica moderna. La premisa central era que el concepto clásico de movimiento no se ajusta al nivel cuántico, ya que los electrones en un átomo no viajan en órbitas claramente definidas. Más bien, su movimiento se difumina de una manera extraña: la transformada de Fourier de su dependencia del tiempo solo involucra aquellas frecuencias que podrían observarse en los saltos cuánticos de su radiación.

El artículo de Heisenberg no admitía ninguna cantidad no observable como la posición exacta del electrón en una órbita en cualquier momento; solo permitió que el teórico hablara sobre los componentes de Fourier del movimiento. Dado que los componentes de Fourier no estaban definidos en las frecuencias clásicas, no podían usarse para construir una trayectoria exacta, por lo que el formalismo no podía responder ciertas preguntas demasiado precisas sobre dónde estaba el electrón o qué tan rápido iba.

Según un relato: el artículo de "Heisenberg' marcó un alejamiento radical de los intentos anteriores de resolver problemas atómicos haciendo uso únicamente de cantidades observables. "Todos mis escasos esfuerzos se dirigen a eliminar y reemplazar adecuadamente el concepto de las trayectorias orbitales que uno no puede observar", escribió en una carta fechada el 9 de julio de 1925."

En realidad, fue Einstein quien planteó el problema por primera vez a Heisenberg en 1926 en su primera discusión real. Einstein había invitado a Heisenberg a su casa para una discusión sobre la mecánica de matrices después de su introducción. Tal como Heisenberg describe la discusión: “De camino a casa, me preguntó sobre mis antecedentes, mis estudios con Sommerfeld. Pero al llegar comenzó de inmediato con una pregunta central sobre el fundamento filosófico de la nueva mecánica cuántica. Me señaló que en mi descripción matemática la noción de 'trayecto de electrones' no ocurrió en absoluto, pero que en una cámara de niebla la trayectoria del electrón puede, por supuesto, observarse directamente. Le parecía absurdo afirmar que efectivamente había un camino de electrones en la cámara de niebla, pero ninguno en el interior del átomo." En esta situación, por supuesto, nosotros [Heisenberg y Bohr] tuvimos muchas discusiones, discusiones difíciles, porque todos sentimos que el esquema matemático de la mecánica cuántica u ondulatoria ya era definitivo. No se podría cambiar, y tendríamos que hacer todos nuestros cálculos a partir de este esquema. Por otro lado, nadie sabía cómo representar en este esquema un caso tan simple como el camino de un electrón a través de una cámara de niebla."

En marzo de 1926, trabajando en el instituto de Bohr, Heisenberg se dio cuenta de que la no conmutatividad implica el principio de incertidumbre. Esta implicación proporcionó una interpretación física clara de la no conmutatividad y sentó las bases de lo que se conoció como la interpretación de Copenhague de la mecánica cuántica. Heisenberg mostró que la relación de conmutación implica una incertidumbre, o en el lenguaje de Bohr, una complementariedad. Dos variables cualesquiera que no se conmutan no se pueden medir simultáneamente: cuanto más precisamente se conoce una, menos precisamente se puede conocer la otra. Heisenberg escribió:

Puede expresarse en su forma más simple como sigue: Uno nunca puede saber con precisión perfecta tanto de esos dos factores importantes que determinan el movimiento de una de las partículas más pequeñas, su posición y su velocidad. Es imposible determinar con precisión ambos la posición y la dirección y velocidad de una partícula en el mismo instante.

En su célebre artículo de 1927, "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik" ("Sobre el contenido perceptivo de la cinemática y la mecánica teóricas cuánticas"), Heisenberg estableció esta expresión como la cantidad mínima de perturbación del momento inevitable causada por cualquier medición de posición, pero no dio una definición precisa de las incertidumbres Δx y Δp. En cambio, dio algunas estimaciones plausibles en cada caso por separado. En su conferencia de Chicago refinó su principio:

Delta x,Delta pgtrsim h

()A1)

Kennard en 1927 demostró por primera vez la desigualdad moderna:

sigma _{x}sigma _{p}geq {frac {hbar }{2}}

()A2)

donde $ħ = h / 2 π$ , y $σ x$ , $σ p$ son las desviaciones estándar de posición y momento. Heisenberg solo probó la relación (A2) para el caso especial de estados gaussianos.

Terminología y traducción

A lo largo de la parte principal de su artículo original de 1927, escrito en alemán, Heisenberg usó la palabra "Ungenauigkeit" ("indeterminación"), describir el principio teórico básico. Solo en la nota final cambió a la palabra "Unsicherheit" ("incertidumbre"). Sin embargo, cuando la versión en inglés del libro de texto de Heisenberg, Los principios físicos de la teoría cuántica, se publicó en 1930, la traducción "incertidumbre" se usó, y se convirtió en el término más comúnmente usado en el idioma inglés a partir de entonces.

Microscopio de Heisenberg

El microscopio de rayos gamma de Heisenberg para localizar un electrón (de color azul). El rayo gamma entrante (que se muestra en verde) se dispersa por el electrón hasta el ángulo de apertura del microscopio Silencio. El rayo gamma disperso se muestra en rojo. La óptica clásica muestra que la posición de electrones se puede resolver sólo hasta una incertidumbre Δx que depende de Silencio y la longitud de onda λ de la luz entrante.

El principio es bastante contrario a la intuición, por lo que los primeros estudiantes de la teoría cuántica tenían que estar seguros de que las medidas ingenuas para violarlo siempre serían impracticables. Una forma en la que Heisenberg ilustró originalmente la imposibilidad intrínseca de violar el principio de incertidumbre es utilizando el efecto del observador de un microscopio imaginario como dispositivo de medición.

Imagina a un experimentador tratando de medir la posición y el momento de un electrón disparándole un fotón.

Problema 1 – Si el fotón tiene una longitud de onda corta, y por lo tanto, un gran impulso, la posición se puede medir con precisión. Pero el fotón se dispersa en una dirección al azar, transfiriendo una gran cantidad de impulso al electrón. Si el fotón tiene una larga longitud de onda y un bajo impulso, la colisión no perturba mucho el impulso del electrón, pero la dispersión revelará su posición sólo vagamente.
Problema 2 – Si se utiliza una abertura grande para el microscopio, la ubicación del electrón puede resolverse bien (ver criterio de Rayleigh); pero por el principio de conservación del impulso, el impulso transversal del foton entrante afecta el impulso de la línea de haz del electrón y por lo tanto, el nuevo impulso del electrón resuelve mal. Si se utiliza una pequeña abertura, la exactitud de ambas resoluciones es la otra manera.

La combinación de estas ventajas y desventajas implica que, independientemente de la longitud de onda del fotón y el tamaño de apertura que se usen, el producto de la incertidumbre en la posición medida y el momento medido es mayor o igual a un límite inferior, que es (hasta un pequeño factor numérico) igual a la constante de Planck. Heisenberg no se preocupó de formular el principio de incertidumbre como un límite exacto, y prefirió usarlo en su lugar, como una afirmación cuantitativa heurística, corregida hasta pequeños factores numéricos, lo que hace inevitable la no conmutatividad radicalmente nueva de la mecánica cuántica.

Reacciones críticas

La interpretación de Copenhague de la mecánica cuántica y el Principio de Incertidumbre de Heisenberg fueron, de hecho, vistos como objetivos gemelos por los detractores que creían en un determinismo y un realismo subyacentes. De acuerdo con la interpretación de Copenhague de la mecánica cuántica, no existe una realidad fundamental que describa el estado cuántico, solo una receta para calcular los resultados experimentales. No hay forma de decir cuál es fundamentalmente el estado de un sistema, solo cuál podría ser el resultado de las observaciones.

Albert Einstein creía que la aleatoriedad es un reflejo de nuestra ignorancia de alguna propiedad fundamental de la realidad, mientras que Niels Bohr creía que las distribuciones de probabilidad son fundamentales e irreducibles, y dependen de las medidas que elijamos realizar. Einstein y Bohr debatieron el principio de incertidumbre durante muchos años.

El ideal del observador imparcial

Wolfgang Pauli llamó a la objeción fundamental de Einstein al principio de incertidumbre "el ideal del observador imparcial" (frase traducida del alemán):

"Al igual que la luna tiene una posición definida" Einstein me dijo el invierno pasado, "si miramos o no a la luna, lo mismo también debe mantener los objetos atómicos, ya que no hay una distinción aguda posible entre estos y objetos macroscópicos. La observación no puede crear un elemento de realidad como una posición, debe haber algo contenido en la descripción completa de la realidad física que corresponde a la posibilidad de observar una posición, ya antes de que se haya hecho la observación." Espero, que cité correctamente a Einstein; siempre es difícil citar a alguien fuera de memoria con quien uno no está de acuerdo. Es precisamente este tipo de postulado que yo llamo el ideal del observador separado.
Carta de Pauli a Niels Bohr, 15 de febrero de 1955

La hendidura de Einstein

El primero de los experimentos mentales de Einstein que desafió el principio de incertidumbre fue el siguiente:

Considere una partícula que pasa por una ranura de ancho

d

. La hendidura introduce una incertidumbre en el impulso de aproximadamente

h / d

porque la partícula pasa por la pared. Pero vamos a determinar el impulso de la partícula midiendo el retroceso de la pared. Al hacerlo, encontramos el impulso de la partícula a la precisión arbitraria mediante la conservación del impulso.

La respuesta de Bohr fue que la pared también es mecánica cuántica, y que para medir el retroceso con precisión $Δ p$ , el el momento de la pared debe conocerse con esta precisión antes de que la partícula pase a través de ella. Esto introduce una incertidumbre en la posición de la pared y por lo tanto la posición de la rendija igual a $h / Δ p$ , y si el momento de la pared se conoce con suficiente precisión para medir el retroceso, la posición de la rendija es lo suficientemente incierta como para no permitir una medición de posición.

Richard Feynman proporciona un análisis similar con partículas que se difractan a través de múltiples rendijas.

Caja de Einstein

Bohr estuvo presente cuando Einstein propuso el experimento mental que se conoce como la caja de Einstein. Einstein argumentó que "la ecuación de incertidumbre de Heisenberg implicaba que la incertidumbre en el tiempo estaba relacionada con la incertidumbre en la energía, y el producto de los dos estaba relacionado con la constante de Planck". Considere, dijo, una caja ideal, forrada con espejos para que pueda contener luz indefinidamente. La caja podía pesarse antes de que un mecanismo de relojería abriera un obturador ideal en un instante elegido para permitir que escapara un solo fotón. "Ahora sabemos, explicó Einstein, exactamente el momento en que el fotón salió de la caja." "Ahora, pesa la caja nuevamente. El cambio de masa indica la energía de la luz emitida. De esta manera, dijo Einstein, se podría medir la energía emitida y el tiempo en que fue liberada con cualquier precisión deseada, en contradicción con el principio de incertidumbre."

Bohr pasó una noche sin dormir considerando este argumento y finalmente se dio cuenta de que era erróneo. Señaló que si la caja fuera a pesarse, digamos con un resorte y un puntero en una balanza, "dado que la caja debe moverse verticalmente con un cambio en su peso, habrá incertidumbre en su velocidad vertical y por lo tanto una incertidumbre en su altura sobre la mesa... Además, la incertidumbre sobre la elevación sobre la superficie de la Tierra resultará en una incertidumbre en la velocidad del reloj," debido a la propia teoría de Einstein del efecto de la gravedad sobre el tiempo. "A través de esta cadena de incertidumbres, Bohr demostró que el experimento de la caja de luz de Einstein no podía medir simultáneamente con exactitud la energía del fotón y el tiempo de su escape".

Paradoja EPR para partículas entrelazadas

Bohr se vio obligado a modificar su comprensión del principio de incertidumbre después de otro experimento mental de Einstein. En 1935, Einstein, Podolsky y Rosen publicaron un análisis de partículas entrelazadas ampliamente separadas (paradoja EPR). Einstein se dio cuenta de que medir una partícula alteraría la distribución de probabilidad de la otra, pero aquí la otra partícula no podría verse perturbada. Este ejemplo llevó a Bohr a revisar su comprensión del principio y concluyó que la incertidumbre no fue causada por una interacción directa.

Pero Einstein llegó a conclusiones de mayor alcance a partir del mismo experimento mental. Él creía que la "suposición básica natural" que una descripción completa de la realidad tendría que predecir los resultados de los experimentos a partir de "cantidades deterministas que cambian localmente" y por tanto tendría que incluir más información que la máxima posible permitida por el principio de incertidumbre.

En 1964, John Stewart Bell demostró que esta suposición se puede falsear, ya que implicaría una cierta desigualdad entre las probabilidades de diferentes experimentos. Los resultados experimentales confirman las predicciones de la mecánica cuántica, descartando la suposición básica de Einstein que lo llevó a sugerir sus variables ocultas. Estas variables ocultas pueden estar "ocultas" debido a una ilusión que ocurre durante las observaciones de objetos que son demasiado grandes o demasiado pequeños. Esta ilusión se puede comparar con las aspas de un ventilador giratorio que parecen aparecer y desaparecer en diferentes lugares y, a veces, parecen estar en el mismo lugar al mismo tiempo cuando se observan. Esta misma ilusión se manifiesta en la observación de partículas subatómicas. Tanto las aspas del ventilador como las partículas subatómicas se mueven tan rápido que el observador ve la ilusión. Por lo tanto, es posible que haya previsibilidad del comportamiento y las características de las partículas subatómicas en un dispositivo de registro capaz de rastrear a muy alta velocidad... Irónicamente, este hecho es una de las mejores pruebas que respaldan la filosofía de Karl Popper. de invalidación de una teoría por experimentos de falsación. Es decir, aquí el "supuesto básico" de Einstein; se falsificó mediante experimentos basados en las desigualdades de Bell. Para las objeciones de Karl Popper a la propia desigualdad de Heisenberg, véase más abajo.

Si bien es posible suponer que las predicciones de la mecánica cuántica se deben a variables ocultas no locales y, de hecho, David Bohm inventó tal formulación, esta resolución no es satisfactoria para la gran mayoría de los físicos. La cuestión de si un resultado aleatorio está predeterminado por una teoría no local puede ser filosófica y potencialmente intratable. Si las variables ocultas no estuvieran restringidas, podrían ser solo una lista de dígitos aleatorios que se usan para producir los resultados de la medición. Para que sea sensato, la suposición de variables ocultas no locales a veces se complementa con una segunda suposición: que el tamaño del universo observable pone un límite a los cálculos que pueden hacer estas variables. Una teoría no local de este tipo predice que una computadora cuántica encontraría obstáculos fundamentales al intentar factorizar números de aproximadamente 10.000 dígitos o más; una tarea potencialmente alcanzable en la mecánica cuántica.

Críticas de Popper

Karl Popper abordó el problema de la indeterminación como un lógico y realista metafísico. No estuvo de acuerdo con la aplicación de las relaciones de incertidumbre a partículas individuales en lugar de conjuntos de partículas preparadas de forma idéntica, y se refirió a ellas como "relaciones de dispersión estadísticas". En esta interpretación estadística, una medida particular puede hacerse con una precisión arbitraria sin invalidar la teoría cuántica. Esto contrasta directamente con la interpretación de Copenhague de la mecánica cuántica, que no es determinista pero carece de variables ocultas locales.

En 1934, Popper publicó Zur Kritik der Ungenauigkeitsrelationen (Crítica de las relaciones de incertidumbre) en Naturwissenschaften, y en el mismo año Logik der Forschung (traducido y actualizado por el autor como The Logic of Scientific Discovery en 1959), esbozando sus argumentos a favor de la interpretación estadística. En 1982, desarrolló aún más su teoría en Teoría cuántica y el cisma en física, escribiendo:

[La fórmula de Heisenberg] son, más allá de toda duda, derivados fórmulas estadísticas de la teoría cuántica. Pero han sido habitualmente malinterpretado por aquellos teóricos cuánticos que dijeron que estas fórmulas pueden ser interpretadas como la determinación de algún límite superior al precisión de nuestras mediciones. [con énfasis original]

Popper propuso un experimento para falsificar las relaciones de incertidumbre, aunque luego retiró su versión inicial después de discusiones con Weizsäcker, Heisenberg y Einstein; este experimento puede haber influido en la formulación del experimento EPR.

Incertidumbre de muchos mundos

La interpretación de muchos mundos esbozada originalmente por Hugh Everett III en 1957 pretende en parte reconciliar las diferencias entre los puntos de vista de Einstein y Bohr al reemplazar el colapso de la función de onda de Bohr con un conjunto de universos deterministas e independientes cuya distribución está gobernada por funciones de onda y la ecuación de Schrödinger. Por lo tanto, la incertidumbre en la interpretación de muchos mundos se deriva de que cada observador dentro de cualquier universo no tiene conocimiento de lo que sucede en los otros universos.

Libre albedrío

Algunos científicos, incluidos Arthur Compton y Martin Heisenberg, han sugerido que el principio de incertidumbre, o al menos la naturaleza probabilística general de la mecánica cuántica, podría ser evidencia del modelo de dos etapas del libre albedrío. Sin embargo, una crítica es que, aparte del papel básico de la mecánica cuántica como base para la química, los mecanismos biológicos no triviales que requieren mecánica cuántica son poco probables, debido al rápido tiempo de decoherencia de los sistemas cuánticos a temperatura ambiente. Los defensores de esta teoría dicen comúnmente que esta decoherencia es superada por los subespacios libres de decoherencia y filtrado que se encuentran en las células biológicas.

Termodinámica

Hay razones para creer que violar el principio de incertidumbre también implica fuertemente la violación de la segunda ley de la termodinámica. Véase la paradoja de Gibbs.

Contenido relacionado

Más resultados...

Principio de incertidumbre

Introducción

Interpretación de la mecánica ondulatoria

Interpretación de la mecánica de matrices

Límite de Heisenberg

Relaciones de incertidumbre de Robertson-Schrödinger

Estados mixtos

Las relaciones de incertidumbre Maccone-Pati

Mejora de la relación de incertidumbre de Robertson-Schrödinger basada en descomposiciones de la matriz de densidad

Espacio de fase

Ejemplos

Un contraejemplo

Ejemplos

Estados estacionarios del oscilador armónico cuántico

Osciladores armónicos cuánticos con condición inicial gaussiana

Estados coherentes

Partícula en una caja

Impulso constante

Relaciones de incertidumbre adicional

Errores sistemáticos y estadísticos

Principio de incertidumbre entrópica cuántica

Relación de incertidumbre con tres componentes de momento angular

Análisis armónico

Procesamiento de señales

Transformada discreta de Fourier

Teorema de Benedictis

Principio de incertidumbre de Hardy

Historia

Terminología y traducción

Microscopio de Heisenberg

Reacciones críticas

El ideal del observador imparcial

La hendidura de Einstein

Caja de Einstein

Paradoja EPR para partículas entrelazadas

Críticas de Popper

Incertidumbre de muchos mundos

Libre albedrío

Termodinámica

Contenido relacionado

Calorimetría

Superconductividad a alta temperatura

Aeronáutica