Presión de radiación

ImprimirCitar

Presión ejercida sobre cualquier superficie expuesta a la radiación electromagnética

Fuerza en un reflector resulta de reflejar el flujo de fotones

Presión de radiación (también conocida como presión de luz) es la presión mecánica ejercida sobre cualquier superficie debido al intercambio de momento entre el objeto y el campo electromagnético. Esto incluye el momento de la luz o la radiación electromagnética de cualquier longitud de onda que es absorbida, reflejada o emitida de otro modo (por ejemplo, radiación de cuerpo negro) por la materia en cualquier escala (desde objetos macroscópicos hasta partículas de polvo y moléculas de gas). La fuerza asociada se denomina fuerza de presión de radiación o, a veces, simplemente fuerza de la luz.

Las fuerzas generadas por la presión de la radiación son generalmente demasiado pequeñas para notarse en circunstancias cotidianas; sin embargo, son importantes en algunos procesos físicos y tecnologías. Esto incluye particularmente a los objetos en el espacio exterior, donde suele ser la principal fuerza que actúa sobre los objetos además de la gravedad, y donde el efecto neto de una fuerza diminuta puede tener un gran efecto acumulativo durante largos períodos de tiempo. Por ejemplo, si se hubieran ignorado los efectos de la presión de radiación del Sol sobre la nave espacial del programa Viking, la nave espacial no habría visto a Marte. órbita por unos 15.000 km (9.300 mi). La presión de radiación de la luz de las estrellas también es crucial en una serie de procesos astrofísicos. La importancia de la presión de radiación aumenta rápidamente a temperaturas extremadamente altas y, a veces, puede eclipsar la presión de gas habitual, por ejemplo, en interiores estelares y armas termonucleares. Además, se han sugerido grandes láseres que operan en el espacio como un medio para propulsar embarcaciones de vela con propulsión impulsada por haz.

Las fuerzas de presión de radiación son la base de la tecnología láser y las ramas de la ciencia que dependen en gran medida de los láseres y otras tecnologías ópticas. Eso incluye, entre otros, biomicroscopía (donde la luz se usa para irradiar y observar microbios, células y moléculas), óptica cuántica y optomecánica (donde la luz se usa para sondear y controlar objetos como átomos, qubits y objetos cuánticos macroscópicos).). Las aplicaciones directas de la fuerza de presión de la radiación en estos campos son, por ejemplo, el enfriamiento por láser (tema del Premio Nobel de Física de 1997), el control cuántico de objetos macroscópicos y átomos (Premio Nobel de Física de 2012), la interferometría (Premio Nobel de Física de 2017). Física) y pinzas ópticas (Premio Nobel de Física 2018).

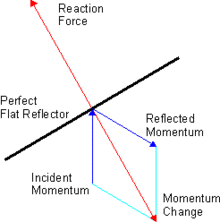
La presión de radiación se puede explicar igualmente considerando el momento de un campo electromagnético clásico o en términos de los momentos de fotones, partículas de luz. La interacción de ondas electromagnéticas o fotones con la materia puede implicar un intercambio de momento. Debido a la ley de conservación de la cantidad de movimiento, cualquier cambio en la cantidad de movimiento total de las ondas o fotones debe implicar un cambio igual y opuesto en la cantidad de movimiento de la materia con la que interactúa (tercera ley de movimiento de Newton), como es ilustrado en la figura adjunta para el caso de la luz perfectamente reflejada por una superficie. Esta transferencia de cantidad de movimiento es la explicación general de lo que llamamos presión de radiación.

Descubrimiento

Johannes Kepler presentó el concepto de presión de radiación en 1619 para explicar la observación de que la cola de un cometa siempre apunta en dirección contraria al Sol.

La afirmación de que la luz, como radiación electromagnética, tiene la propiedad de la cantidad de movimiento y, por lo tanto, ejerce una presión sobre cualquier superficie expuesta a ella fue publicada por James Clerk Maxwell en 1862 y probada experimentalmente por el físico ruso Pyotr Lebedev en 1900 y por Ernest Fox Nichols y Gordon Ferrie Hull en 1901. La presión es muy pequeña, pero se puede detectar al permitir que la radiación caiga sobre una paleta de metal reflectante delicadamente equilibrada en un radiómetro de Nichols (esto no debe confundirse con el radiómetro de Crookes, cuyo movimiento característico no es causado por la presión de radiación sino por el impacto de las moléculas de gas).

Teoría

La presión de radiación puede verse como una consecuencia de la conservación del momento dado el momento atribuido a la radiación electromagnética. Ese momento se puede calcular igualmente bien sobre la base de la teoría electromagnética o de los momentos combinados de una corriente de fotones, dando resultados idénticos como se muestra a continuación.

Presión de radiación del impulso de una onda electromagnética

Según la teoría del electromagnetismo de Maxwell, una onda electromagnética transporta un impulso, que se transferirá a una superficie opaca sobre la que golpea.

El flujo energético (irradiance) de una onda plana se calcula utilizando el vector Poynting $mathbf{S} = mathbf{E}timesmathbf{H}$ , cuya magnitud denotamos S. S dividida por la velocidad de la luz es la densidad del impulso lineal por área unidad (presión) del campo electromagnético. Así que, dimensionalmente, el vector Poynting es S=poder/zona=Tasa de trabajo/zona=ΔF/ΔtΔx/zona, que es la velocidad de la luz, c=x/Δt, presión de tiempos ΔF/rea. Esa presión se experimenta como presión de radiación en la superficie:

{displaystyle P_{text{incident}}={frac {langle Srangle }{c}}={frac {I_{f}}{c}}}

Donde $P$ es presión (normalmente en Pascals), $I_f$ es el incidente irradiancia (generalmente en W/m²) y $c$ es la velocidad de la luz en vacío. Aquí, 1/c. 3.34 N/GW.

Si la superficie es plana en un ángulo α con respecto a la onda incidente, la intensidad a través de la superficie se reducirá geométricamente por el coseno de ese ángulo y el componente de la fuerza de radiación contra la superficie también se reducirá por el coseno de α, resultando en una presión:

{displaystyle P_{text{incident}}={frac {I_{f}}{c}}cos ^{2}alpha }

El impulso de la onda incidente está en la misma dirección que esa onda. Pero solo la componente de ese impulso normal a la superficie contribuye a la presión sobre la superficie, como se indicó anteriormente. La componente de esa fuerza tangente a la superficie no se llama presión.

Presión de radiación por reflexión

El tratamiento anterior para una onda incidente representa la presión de radiación experimentada por un cuerpo negro (totalmente absorbente). Si la onda se refleja especularmente, entonces el retroceso debido a la onda reflejada contribuirá aún más a la presión de radiación. En el caso de un reflector perfecto, esta presión será idéntica a la presión provocada por la onda incidente:

{displaystyle P_{text{emitted}}={frac {I_{f}}{c}}}

esto duplicando la presión de radiación neta en la superficie:

{displaystyle P_{text{net}}=P_{text{incident}}+P_{text{emitted}}=2{frac {I_{f}}{c}}}

Para una superficie parcialmente reflectante, el segundo término debe multiplicarse por la reflectividad (también conocido como coeficiente de intensidad de reflexión), de modo que el aumento sea menos del doble. Para una superficie de reflexión difusa, se deben tener en cuenta los detalles de la reflexión y la geometría, lo que de nuevo da como resultado un aumento de la presión de radiación neta de menos del doble.

Presión de radiación por emisión

Así como una onda reflejada por un cuerpo contribuye a la presión de radiación neta experimentada, un cuerpo que emite radiación por sí mismo (en lugar de la reflejada) obtiene nuevamente una presión de radiación dada por la irradiancia de esa emisión en la dirección normal a la superficie I_e:

{displaystyle P_{text{emitted}}={frac {I_{text{e}}}{c}}}

La emisión puede provenir de radiación de cuerpo negro o cualquier otro mecanismo radiativo. Dado que todos los materiales emiten radiación de cuerpo negro (a menos que sean totalmente reflectantes o estén en el cero absoluto), esta fuente de presión de radiación es omnipresente pero generalmente pequeña. Sin embargo, debido a que la radiación de cuerpo negro aumenta rápidamente con la temperatura (como la cuarta potencia de la temperatura, dada por la ley de Stefan-Boltzmann), la presión de radiación debida a la temperatura de un objeto muy caliente (o debido a la radiación de cuerpo negro entrante de forma similar) ambientes calurosos) pueden volverse significativos. Esto es importante en los interiores estelares.

Presión de radiación en términos de fotones

La radiación electromagnética se puede ver en términos de partículas en lugar de ondas; estas partículas se conocen como fotones. Los fotones no tienen masa en reposo; sin embargo, los fotones nunca están en reposo (se mueven a la velocidad de la luz) y, no obstante, adquieren un impulso que viene dado por:

{displaystyle p={dfrac {h}{lambda }}={frac {E_{p}}{c}},}

donde p es el momento, h es la constante de Planck, λ es la longitud de onda y c es la velocidad de la luz en el vacío. Y E_p es la energía de un único fotón dada por:

{displaystyle E_{p}=hnu ={frac {hc}{lambda }}}

La presión de radiación nuevamente se puede ver como la transferencia del momento de cada fotón a la superficie opaca, más el momento debido a un (posible) fotón de retroceso para una superficie (parcialmente) reflectante. Dado que una onda incidente de irradiancia I_f sobre un área A tiene una potencia de I_fA , esto implica un flujo de I_f/E_p fotones por segundo por unidad de área que golpean la superficie. Combinando esto con la expresión anterior para el impulso de un solo fotón, se obtienen las mismas relaciones entre la irradiancia y la presión de radiación descritas anteriormente utilizando el electromagnetismo clásico. Y nuevamente, los fotones reflejados o emitidos contribuirán a la presión de radiación neta de manera idéntica.

Compresión en un campo de radiación uniforme

En general, la presión de las ondas electromagnéticas se puede obtener a partir de la desaparición de la traza del tensor de tensión electromagnético: dado que esta traza es igual a 3P − u, obtenemos

{displaystyle P={frac {u}{3}},}

donde u es la energía de radiación por unidad de volumen.

Esto también se puede demostrar en el caso concreto de la presión ejercida sobre superficies de un cuerpo en equilibrio térmico con su entorno, a una temperatura T: el cuerpo estará rodeado por un campo de radiación uniforme descrito por la ley de radiación de cuerpo negro de Planck y experimentará una presión de compresión debido a la radiación incidente, su reflexión y su propia emisión de cuerpo negro. A partir de ahí se puede demostrar que la presión resultante es igual a un tercio de la energía radiante total por unidad de volumen en el espacio circundante.

Usando la ley de Stefan-Boltzmann, esto se puede expresar como

{displaystyle P_{text{compress}}={frac {u}{3}}={frac {4sigma }{3c}}T^{4},}

Donde $sigma$ es la constante Stefan-Boltzmann.

Presión de radiación solar

La presión de la radiación solar se debe a la radiación del Sol a distancias más cercanas, especialmente dentro del Sistema Solar. (La presión de radiación de la luz solar sobre la Tierra es muy pequeña: equivale a la que ejerce aproximadamente un miligramo sobre un área de 1 metro cuadrado, o 10 μN/m², o 10^{- 10} atmósferas). Si bien actúa sobre todos los objetos, su efecto neto es generalmente mayor en los cuerpos más pequeños, ya que tienen una mayor proporción de área superficial a masa. Todas las naves espaciales experimentan tal presión, excepto cuando están detrás de la sombra de un cuerpo en órbita más grande.

La presión de la radiación solar sobre los objetos cercanos a la Tierra se puede calcular utilizando la irradiancia del Sol a 1 AU, conocida como la constante solar o G_SC, cuyo valor se establece en 1361 W/m² a partir de 2011.

Todas las estrellas tienen una distribución de energía espectral que depende de la temperatura de su superficie. La distribución es aproximadamente la de la radiación de cuerpo negro. Esta distribución debe tenerse en cuenta al calcular la presión de radiación o identificar materiales reflectores para optimizar una vela solar, por ejemplo.

Las presiones solares momentáneas o de una hora de duración pueden escalar debido a la liberación de erupciones solares y eyecciones de masa coronal, pero los efectos siguen siendo esencialmente inconmensurables en relación con la órbita terrestre. Sin embargo, estas presiones persisten durante eones, de modo que acumulativamente han producido un movimiento medible en la órbita del sistema tierra-luna.

Presiones de absorción y reflexión

La presión de radiación solar a la distancia de la Tierra al Sol se puede calcular dividiendo la constante solar G_SC (arriba) por la velocidad de la luz c. Para una lámina absorbente que mira hacia el Sol, esto es simplemente:

{displaystyle P={frac {G_{text{SC}}}{c}}approx 4.5cdot 10^{-6}~{text{Pa}}=4.5~mu {text{Pa}}.}

Este resultado está en pascales, equivalente a N/m² (newtons por metro cuadrado). Para una hoja en un ángulo α con el Sol, el área efectiva A de una hoja se reduce por un factor geométrico que resulta en una fuerza en la dirección de la luz solar de:

{displaystyle F={frac {G_{text{SC}}}{c}}(Acos alpha).}

Para encontrar la componente de esta fuerza normal a la superficie, se debe aplicar otro factor de coseno que dé como resultado una presión P en la superficie de:

{displaystyle P={frac {F}{A}}={frac {G_{text{SC}}}{c}}cos ^{2}alpha.}

Tenga en cuenta, sin embargo, que para tener en cuenta el efecto neto de la radiación solar en una nave espacial, por ejemplo, sería necesario considerar la fuerza total (en la dirección que se aleja del Sol) dada por la ecuación anterior, en lugar de solo el componente normal a la superficie que identificamos como "presión".

La constante solar se define para la radiación del Sol a la distancia de la Tierra, también conocida como una unidad astronómica (au). En consecuencia, a una distancia de R unidades astronómicas (siendo entonces R adimensional), aplicando la ley del inverso del cuadrado, nos encontraríamos con:

{displaystyle P={frac {G_{text{SC}}}{cR^{2}}}cos ^{2}alpha.}

Finalmente, considerando que no es una superficie absorbente sino perfectamente reflectante, la presión se duplica debido a la onda reflejada, resultando en:

{displaystyle P=2{frac {G_{text{SC}}}{cR^{2}}}cos ^{2}alpha.}

Tenga en cuenta que, a diferencia del caso de un material absorbente, la fuerza resultante sobre un cuerpo reflectante viene dada exactamente por esta presión que actúa normal a la superficie, con las fuerzas tangenciales de las ondas incidente y reflejada anulándose entre sí. En la práctica, los materiales no reflejan ni absorben totalmente, por lo que la fuerza resultante será un promedio ponderado de las fuerzas calculadas con estas fórmulas.

Presión de radiación solar calculada sobre reflector perfecto a la incidencia normal (α = 0)
Distancia al Sol	Presión de radiación en μPa (μN/m²)
0.20 au	227
0.39 au (Mercury)	59,7
0,72 au (Venus)	17,5
1.00 au (Tierra)	9.08
1.52 au (Mars)	3.93
3.00 au (asteroide típico)	1.01
5.20 au (Jupiter)	0.34

Perturbaciones de presión de radiación

La presión de la radiación solar es una fuente de perturbaciones orbitales. Afecta significativamente las órbitas y trayectorias de los cuerpos pequeños, incluidas todas las naves espaciales.

La presión de la radiación solar afecta a los cuerpos en gran parte del Sistema Solar. Los cuerpos pequeños se ven más afectados que los grandes debido a su menor masa en relación con su área de superficie. Las naves espaciales se ven afectadas junto con los cuerpos naturales (cometas, asteroides, granos de polvo, moléculas de gas).

La presión de radiación genera fuerzas y torsiones en los cuerpos que pueden cambiar sus movimientos de traslación y rotación. Los cambios de traslación afectan las órbitas de los cuerpos. Las tasas de rotación pueden aumentar o disminuir. Los cuerpos agregados libremente pueden romperse bajo altas tasas de rotación. Los granos de polvo pueden abandonar el Sistema Solar o girar en espiral hacia el Sol.

Un cuerpo completo generalmente se compone de numerosas superficies que tienen diferentes orientaciones en el cuerpo. Las facetas pueden ser planas o curvas. Tendrán diferentes áreas. Pueden tener propiedades ópticas que difieren de otros aspectos.

En un momento determinado, algunas facetas están expuestas al sol y otras están en la sombra. Cada superficie expuesta al Sol refleja, absorbe y emite radiación. Las facetas en la sombra están emitiendo radiación. La suma de las presiones en todas las facetas define la fuerza neta y el par en el cuerpo. Estos se pueden calcular utilizando las ecuaciones de las secciones anteriores.

El efecto Yarkovsky afecta la traslación de un cuerpo pequeño. Es el resultado de una cara que sale de la exposición solar a una temperatura más alta que una cara que se acerca a la exposición solar. La radiación emitida por la cara más cálida es más intensa que la de la cara opuesta, lo que da como resultado una fuerza neta sobre el cuerpo que afecta su movimiento.

El efecto YORP es una colección de efectos que amplían el concepto anterior del efecto Yarkovsky, pero de naturaleza similar. Afecta las propiedades de espín de los cuerpos.

El efecto Poynting-Robertson se aplica a partículas del tamaño de un grano. Desde la perspectiva de un grano de polvo que gira alrededor del Sol, la radiación del Sol parece provenir de una dirección ligeramente hacia adelante (aberración de la luz). Por lo tanto, la absorción de esta radiación conduce a una fuerza con un componente en contra de la dirección del movimiento. (El ángulo de aberración es pequeño, ya que la radiación se mueve a la velocidad de la luz, mientras que el grano de polvo se mueve muchos órdenes de magnitud más lento). El resultado es una espiral gradual de granos de polvo hacia el Sol. Durante largos períodos de tiempo, este efecto limpia gran parte del polvo del Sistema Solar.

Aunque es bastante pequeña en comparación con otras fuerzas, la fuerza de presión de radiación es inexorable. Durante largos períodos de tiempo, el efecto neto de la fuerza es sustancial. Tales presiones débiles pueden producir efectos marcados sobre partículas diminutas como iones de gas y electrones, y son esenciales en la teoría de la emisión de electrones del Sol, del material cometario, etc.

Debido a que la relación entre el área superficial y el volumen (y, por lo tanto, la masa) aumenta con la disminución del tamaño de las partículas, las partículas de polvo (del tamaño de un micrómetro) son susceptibles a la presión de la radiación incluso en el sistema solar exterior. Por ejemplo, la evolución de los anillos exteriores de Saturno está significativamente influenciada por la presión de radiación.

Como consecuencia de la presión de la luz, Einstein en 1909 predijo la existencia de "rozamiento por radiación", que se opondría al movimiento de la materia. Escribió: 'la radiación ejercerá presión en ambos lados de la placa. Las fuerzas de presión ejercidas sobre los dos lados son iguales si la placa está en reposo. Sin embargo, si está en movimiento, se reflejará más radiación en la superficie que está adelante durante el movimiento (superficie frontal) que en la superficie posterior. La fuerza de presión que actúa hacia atrás ejercida sobre la superficie frontal es, por lo tanto, mayor que la fuerza de presión que actúa sobre la parte posterior. Por tanto, como resultante de las dos fuerzas, queda una fuerza que contrarresta el movimiento de la placa y que aumenta con la velocidad de la placa. Llamaremos a esta resultante 'rozamiento por radiación' en resumen."

Velas solares

La navegación solar, un método experimental de propulsión de naves espaciales, utiliza la presión de radiación del Sol como fuerza motriz. La idea del viaje interplanetario de la luz fue mencionada por Julio Verne en De la Tierra a la Luna.

Una vela refleja alrededor del 90 % de la radiación incidente. El 10% que se absorbe se irradia desde ambas superficies, y la proporción emitida por la superficie no iluminada depende de la conductividad térmica de la vela. Una vela tiene curvatura, irregularidades en la superficie y otros factores menores que afectan su desempeño.

La Agencia de Exploración Aeroespacial de Japón (JAXA) ha desplegado con éxito una vela solar en el espacio, que ya ha logrado impulsar su carga útil con el proyecto IKAROS.

Efectos cósmicos de la presión de radiación

La presión de la radiación ha tenido un efecto importante en el desarrollo del cosmos, desde el nacimiento del universo hasta la formación continua de estrellas y la formación de nubes de polvo y gases en una amplia gama de escalas.

El universo primitivo

La época de los fotones es una fase en la que la energía del universo estuvo dominada por fotones, entre 10 segundos y 380 000 años después del Big Bang.

Formación y evolución de galaxias

El Pilares de la Creación nubes dentro de la nebulosa águila con forma de presión de radiación y vientos estelares.

El proceso de formación y evolución de galaxias comenzó temprano en la historia del cosmos. Las observaciones del universo primitivo sugieren fuertemente que los objetos crecieron de abajo hacia arriba (es decir, los objetos más pequeños se fusionaron para formar otros más grandes). A medida que las estrellas se forman y se convierten en fuentes de radiación electromagnética, la presión de radiación de las estrellas se convierte en un factor en la dinámica del material circunestelar restante.

Nubes de polvo y gases

La compresión gravitacional de las nubes de polvo y gases está fuertemente influenciada por la presión de la radiación, especialmente cuando las condensaciones conducen al nacimiento de estrellas. Las estrellas jóvenes más grandes que se forman dentro de las nubes comprimidas emiten intensos niveles de radiación que desplazan las nubes, provocando dispersión o condensaciones en las regiones cercanas, lo que influye en las tasas de natalidad en esas regiones cercanas.

Grupos de estrellas

Las estrellas se forman predominantemente en regiones de grandes nubes de polvo y gases, lo que da lugar a cúmulos estelares. La presión de radiación de las estrellas miembro finalmente dispersa las nubes, lo que puede tener un profundo efecto en la evolución del cúmulo.

Muchos cúmulos abiertos son inherentemente inestables, con una masa lo suficientemente pequeña como para que la velocidad de escape del sistema sea menor que la velocidad promedio de las estrellas constituyentes. Estos grupos se dispersarán rápidamente en unos pocos millones de años. En muchos casos, la extracción del gas del que se formó el cúmulo por la presión de radiación de las estrellas jóvenes y calientes reduce la masa del cúmulo lo suficiente como para permitir una rápida dispersión.

Un disco protoplanetario con una región central despejada (concepción del artista).

Formación de estrellas

La formación de estrellas es el proceso mediante el cual las regiones densas dentro de las nubes moleculares en el espacio interestelar colapsan para formar estrellas. Como rama de la astronomía, la formación estelar incluye el estudio de las nubes moleculares gigantes y medianas interestelares (GMC) como precursores del proceso de formación estelar, y el estudio de protoestrellas y objetos estelares jóvenes como sus productos inmediatos. La teoría de la formación estelar, además de dar cuenta de la formación de una sola estrella, también debe tener en cuenta las estadísticas de las estrellas binarias y la función de masa inicial.

Sistemas planetarios estelares

En general, se cree que los sistemas planetarios se forman como parte del mismo proceso que da como resultado la formación de estrellas. Un disco protoplanetario se forma por el colapso gravitacional de una nube molecular, llamada nebulosa solar, y luego evoluciona a un sistema planetario por colisiones y captura gravitacional. La presión de la radiación puede despejar una región en las inmediaciones de la estrella. A medida que continúa el proceso de formación, la presión de radiación continúa desempeñando un papel en la distribución de la materia. En particular, el polvo y los granos pueden entrar en espiral hacia la estrella o escapar del sistema estelar bajo la acción de la presión de radiación.

Comet Hale-Bopp (C/1995 O1). La presión de radiación y los efectos del viento solar en las colas de polvo y gas son claramente vistos.

Interiores estelares

En los interiores estelares las temperaturas son muy altas. Los modelos estelares predicen una temperatura de 15 MK en el centro del Sol, y en los núcleos de las estrellas supergigantes la temperatura puede superar los 1 GK. Como la presión de radiación escala como la cuarta potencia de la temperatura, se vuelve importante a estas altas temperaturas. En el Sol, la presión de radiación sigue siendo bastante pequeña en comparación con la presión del gas. En las estrellas no degeneradas más pesadas, la presión de radiación es el componente de presión dominante.

Cometas

La presión de la radiación solar afecta fuertemente a las colas de los cometas. El calor solar hace que se liberen gases del núcleo del cometa, que también se llevan los granos de polvo. La presión de la radiación y el viento solar alejan el polvo y los gases de la dirección del Sol. Los gases forman una cola generalmente recta, mientras que las partículas de polvo que se mueven más lentamente crean una cola curva más ancha.

Aplicaciones láser de presión de radiación

Pinzas ópticas

Los láseres se pueden utilizar como fuente de luz monocromática con longitud de onda $lambda$ . Con un conjunto de lentes, se puede enfocar el rayo láser a un punto que es $lambda$ en diámetro (o ${displaystyle r=lambda /2}$ ).

La presión de radiación de un láser P = 30 mW con λ = 1064 nm se puede calcular de la siguiente manera.

Área:

{displaystyle A=pi left({frac {lambda }{2}}right)^{2}approx 10^{-12}{text{ m}}^{2},}

fuerza:

{displaystyle F={frac {P}{c}}={frac {30{text{ mW}}}{299792458{text{ m/s}}}}approx 10^{-10}{text{ N}},}

presión:

{displaystyle p={frac {F}{A}}approx {frac {10^{-10}{text{ N}}}{10^{-12}{text{ m}}^{2}}}=100{text{ Pa}}.}

Esto se usa para atrapar o hacer levitar partículas en pinzas ópticas.

Interacciones luz-materia

En esta cavidad optomecánica, la luz está atrapada y mejorada entre dos espejos. Uno de los espejos está unido a una primavera y puede moverse. La fuerza de presión de radiación de la luz que circula en la cavidad puede humedecer o amplificar la oscilación del espejo en la primavera.

La reflexión de un pulso láser desde la superficie de un sólido elástico puede dar lugar a varios tipos de ondas elásticas que se propagan dentro del sólido o líquido. En otras palabras, la luz puede excitar y/o amplificar el movimiento de y en los materiales. Este es el tema de estudio en el campo de la optomecánica. Las ondas más débiles son generalmente las que se generan por la presión de radiación que actúa durante la reflexión de la luz. Tales ondas elásticas inducidas por la presión de la luz se han observado, por ejemplo, dentro de un espejo dieléctrico de ultra alta reflectividad. Estas ondas son la huella digital más básica de una interacción luz-materia sólida en la escala macroscópica. En el campo de la optomecánica de cavidades, la luz queda atrapada y resonantemente mejorada en las cavidades ópticas, por ejemplo, entre espejos. Esto tiene el propósito de mejorar gravemente el poder de la luz y la presión de radiación que puede ejercer sobre objetos y materiales. Se ha realizado el control óptico (es decir, la manipulación del movimiento) de una plétora de objetos: desde haces de kilómetros de largo (como en el interferómetro LIGO) hasta nubes de átomos, y desde trampolines creados con microingeniería hasta superfluidos.

En este sistema optomecánico, la fuerza de presión de radiación se aprovecha para detectar una sola molécula de proteína. La luz láser interactúa con una esfera de vidrio: la fuerza de presión de radiación hace vibrar. La presencia de una sola molécula en la esfera perturba que la vibración (termal) y la perturbación en el movimiento de la esfera se pueden detectar en el espectro oscilador de la izquierda.

Al contrario de excitar o amplificar el movimiento, la luz también puede amortiguar el movimiento de los objetos. El enfriamiento por láser es un método para enfriar materiales muy cerca del cero absoluto mediante la conversión de parte de la energía de movimiento del material en luz. La energía cinética y la energía térmica del material son sinónimos aquí, porque representan la energía asociada con el movimiento browniano del material. Los átomos que viajan hacia una fuente de luz láser perciben un efecto doppler sintonizado con la frecuencia de absorción del elemento objetivo. La presión de radiación sobre el átomo ralentiza el movimiento en una dirección particular hasta que el efecto Doppler sale del rango de frecuencia del elemento, provocando un efecto de enfriamiento general.

Otra área de investigación activa de la interacción láser-materia es la aceleración de la presión de radiación de iones o protones de objetivos de lámina delgada. Se pueden generar haces de alta energía de iones para aplicaciones médicas (por ejemplo, en la terapia de haces de iones) mediante la presión de radiación de pulsos láser cortos en láminas ultrafinas.

Contenido relacionado

Más resultados...