Pozo cuántico

Un pozo cuántico es un pozo potencial con sólo valores de energía discretos.

El modelo clásico utilizado para demostrar un pozo cuántico consiste en confinar partículas, que inicialmente eran libres de moverse en tres dimensiones, a dos dimensiones, obligándolas a ocupar una región plana. Los efectos del confinamiento cuántico tienen lugar cuando el espesor del pozo cuántico se vuelve comparable a la longitud de onda de De Broglie de los portadores (generalmente electrones y huecos), lo que lleva a niveles de energía llamados "subbandas de energía", es decir, los portadores sólo pueden tienen valores de energía discretos.

El concepto de pozo cuántico fue propuesto en 1963 de forma independiente por Herbert Kroemer y por Zhores Alferov y R.F. Kazarinov.

Historia

El pozo cuántico semiconductor fue desarrollado en 1970 por Esaki y Tsu, quienes también inventaron las superredes sintéticas. Sugirieron que una heteroestructura formada por capas delgadas alternas de semiconductores con diferentes bandas prohibidas debería exhibir propiedades interesantes y útiles. Desde entonces, se han dedicado muchos esfuerzos e investigaciones al estudio de la física de los sistemas de pozos cuánticos, así como al desarrollo de dispositivos de pozos cuánticos.

El desarrollo de dispositivos de pozos cuánticos se atribuye en gran medida a los avances en las técnicas de crecimiento de cristales. Esto se debe a que los dispositivos de pozos cuánticos requieren estructuras de alta pureza con pocos defectos. Por lo tanto, tener un gran control sobre el crecimiento de estas heteroestructuras permite el desarrollo de dispositivos semiconductores que pueden tener propiedades muy afinadas.

Los pozos cuánticos y la física de semiconductores han sido un tema candente en la investigación en física. El desarrollo de dispositivos semiconductores que utilizan estructuras formadas por múltiples semiconductores dio lugar a los premios Nobel para Zhores Alferov y Herbert Kroemer en 2000.

La teoría que rodea a los dispositivos de pozos cuánticos ha dado lugar a avances significativos en la producción y eficiencia de muchos componentes modernos, como diodos emisores de luz y transistores, por ejemplo. Hoy en día, estos dispositivos están omnipresentes en los teléfonos móviles, ordenadores y muchos otros dispositivos informáticos modernos.

Fabricación

Los pozos cuánticos se forman en semiconductores al tener un material, como el arseniuro de galio, intercalado entre dos capas de un material con una banda prohibida más amplia, como el arseniuro de aluminio. (Otros ejemplos: una capa de nitruro de indio y galio intercalada entre dos capas de nitruro de galio). Estas estructuras pueden desarrollarse mediante epitaxia de haz molecular o deposición química de vapor con control del espesor de la capa hasta monocapas.

Las películas metálicas delgadas también pueden soportar estados de pozos cuánticos, en particular, capas superpuestas metálicas delgadas que crecen en superficies metálicas y semiconductoras. La interfaz vacío-metal confina el electrón (o hueco) en un lado y, en general, mediante una brecha absoluta con los sustratos semiconductores, o mediante una banda prohibida proyectada con los sustratos metálicos.

Existen tres enfoques principales para hacer crecer un sistema de material QW: enrejado acoplado, con tensión equilibrada y con tensión.

• Lattice-matched system: En un sistema de lattice-matched, el pozo y la barrera tienen una constante de celo similar como el material de sustrato subyacente. Con este método, la diferencia de bandagap hay una dislocación mínima, pero también un cambio mínimo en el espectro de absorción.
• Sistema equilibrado: En un sistema de equilibrio de tensión, el pozo y la barrera se cultivan para que el aumento de la constante de la rejilla de una de las capas se compense por la disminución de la constante de la rejilla en el siguiente comparado con el material del sustrato. La elección del grosor y la composición de las capas afectan a los requerimientos de bandgap y las limitaciones de transporte de portadores. Este enfoque proporciona la mayor flexibilidad en el diseño, ofreciendo un alto número de QW periódicos con mínima relajación de la tensión.
• Sistema estrado: Un sistema tenso se cultiva con pozos y barreras que no son similares en constante de celosía. Un sistema tensado comprime toda la estructura. Como resultado, la estructura sólo puede acomodar unos pocos pozos cuánticos.

Descripción y descripción general

Uno de los sistemas de pozos cuánticos más simples se puede construir insertando una capa delgada de un tipo de material semiconductor entre dos capas de otro con una banda prohibida diferente. Considere, como ejemplo, dos capas de AlGaAs con una banda prohibida grande que rodea una capa delgada de GaAs con una banda prohibida más pequeña. Supongamos que el cambio de material ocurre a lo largo de la dirección z y, por lo tanto, el pozo potencial está a lo largo de la dirección z (sin confinamiento en la dirección x–y avión.). Dado que la banda prohibida del material contenido es menor que la del AlGaAs circundante, se crea un pozo cuántico (pozo potencial) en la región de GaAs. Este cambio en la energía de la banda a través de la estructura puede verse como el cambio en el potencial que sentiría un portador, por lo tanto, los portadores de baja energía pueden quedar atrapados en estos pozos.

Dentro del pozo cuántico, hay estados propios de energía discretos que los portadores pueden tener. Por ejemplo, un electrón en la banda de conducción puede tener menor energía dentro del pozo que la que podría tener en la región AlGaAs de esta estructura. En consecuencia, un electrón en la banda de conducción con baja energía puede quedar atrapado dentro del pozo cuántico. De manera similar, los agujeros en la banda de valencia también pueden quedar atrapados en la parte superior de los pozos potenciales creados en la banda de valencia. Los estados en los que pueden encontrarse los transportistas confinados son estados similares a partículas en una caja.

Física

Los pozos cuánticos y los dispositivos de pozos cuánticos son un subcampo de la física del estado sólido que todavía se estudia e investiga ampliamente en la actualidad. La teoría utilizada para describir tales sistemas utiliza resultados importantes de los campos de la física cuántica, la física estadística y la electrodinámica.

Modelo de pozo infinito

El modelo más simple de un sistema de pozos cuánticos es el modelo de pozos infinitos. En este modelo se supone que las paredes/barreras del pozo potencial son infinitas. Esta aproximación es bastante poco realista, ya que los pozos de potencial creados en los pozos cuánticos son generalmente del orden de unos pocos cientos de milielectronvoltios, lo que es mucho menor que el potencial infinitamente alto supuesto. Sin embargo, como primera aproximación, el modelo de pozo infinito sirve como un modelo simple y útil que proporciona una idea de la física detrás de los pozos cuánticos.

Considerar un cuántico infinito bien orientado en el z- dirección, tal que los portadores en el pozo se limitan en el z- dirección pero libre de moverse x-y avión. elegimos el pozo cuántico para correr ${displaystyle z=0}$ a ${displaystyle z=d}$. Asumimos que los transportistas no tienen potencial dentro del pozo y que el potencial en la región de barrera es infinitamente alto.

La ecuación Schrödinger para portadores en el modelo infinitamente bueno es:

${displaystyle - ¿Qué? ¿Qué?$

Donde ${displaystyle hbar }$ es la constante de Planck dividida por ${displaystyle 2pi}$ y ${displaystyle ¿Qué?$ es la masa efectiva de los transportistas dentro de la región del pozo. La masa efectiva de un transportista es la masa que el electrón "sentele" en su entorno cuántico y generalmente difiere entre diferentes semiconductores ya que el valor de masa efectiva depende en gran medida de la curvatura de la banda. Note que ${displaystyle ¿Qué?$ puede ser la masa efectiva de electrones en un pozo en la banda de conducción o para agujeros en un pozo en la banda de valence.

Soluciones y niveles de energía

Las funciones de onda de la solución no pueden existir en la región de barrera del pozo, debido al potencial infinitamente alto. Por lo tanto, al imponer las siguientes condiciones de contorno, se obtienen las funciones de onda permitidas,

${displaystyle psi (0)=psi (d)=0.}$

Las funciones de onda de solución toman la siguiente forma:

${displaystyle psi _{n}(z)={sqrt {frac {2}{d}sin(k_{n}z)qquad k_{n}={frac {fncHFF} } {d}}$

El subscript ${displaystyle n}$, (${displaystyle n confía0}$) denota el número de cuántico entero y ${displaystyle K_{n}$ es el vector de onda asociado con cada estado, dado arriba. Las energías discretas asociadas son dadas por:

${displaystyle E_{n}={frac {hbar ^{2}k_{n}{2m_{2m_{}={f}={f} {f}} {f}}}} {f} {f}}}} {f}}}}}}} {f}} {f} {f}} {f}}}}}} {f}}}}}}}}} {f}}}}} {f}}}}}}} {f}}}}}} {f}}}}}}}}}}}} {f}}} {f}}}}}} {f}}}}}}}} {f}}}}} {f}} {f}} {f}}}}}}}}}}}} {f}} {f} {f}} {f}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}} {hbar ^{2}{2m_{*}}left({frac {npi}{d}right)}} {2}}}}} {i}} {fn} {fn}}} {fn}}} {fn}}} {f}}}}} {f}}}}} {hbar}}} {hbar}}}}}}}}}}}}}}}} {hbar}}}}} {hbar} {hbar}} {hbar} {hbar} {hbar}}}}}}}}}}}}}} {hbar}}}}}} {h}} {h}} {hbar}}} {h}}}}}}}}}}}}}}}} {h}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {h}}}}} {$

El modelo simple de pozo infinito proporciona un buen punto de partida para analizar la física de los sistemas de pozos cuánticos y los efectos del confinamiento cuántico. El modelo predice correctamente que las energías en el pozo son inversamente proporcionales al cuadrado de la longitud del pozo. Esto significa que un control preciso sobre el ancho de las capas semiconductoras, es decir, la longitud del pozo, permitirá un control preciso de los niveles de energía permitidos para los portadores en los pozos. Esta es una propiedad increíblemente útil para la ingeniería de banda prohibida. Además, el modelo muestra que los niveles de energía son proporcionales a la inversa de la masa efectiva. En consecuencia, los agujeros pesados y los agujeros ligeros tendrán diferentes estados de energía cuando estén atrapados en el pozo. Los agujeros pesados y ligeros surgen cuando coinciden los máximos de las bandas de valencia con diferente curvatura; dando como resultado dos masas efectivas diferentes.

Un inconveniente del modelo de pozo infinito es que predice muchos más estados de energía de los que existen, ya que las paredes de los pozos cuánticos reales son finitas. El modelo también ignora el hecho de que, en realidad, las funciones de onda no llegan a cero en el límite del pozo, sino que "sangran" el nivel del pozo. en la pared (debido al túnel cuántico) y decae exponencialmente a cero. Esta propiedad permite el diseño y producción de superredes y otros dispositivos novedosos de pozos cuánticos y se describe mejor mediante el modelo de pozo finito.

Modelo de pozo finito

El modelo finito bien proporciona un modelo más realista de pozos cuánticos. Aquí las paredes del pozo en la heteroestructura se modelan utilizando un potencial finito ${displaystyle V_{0}$, que es la diferencia en las energías de banda de conducción de los diferentes semiconductores. Puesto que las paredes son finitas y los electrones pueden túnelear en la región de barrera. Por lo tanto, las funciones de onda permitidas penetrarán la pared de la barrera.

Considere un cuántico finito bien orientado en el z- dirección, tal que los portadores en el pozo se limitan en el z- dirección pero libre de moverse x-y avión. Elegimos el pozo cuántico para huir ${displaystyle z=0}$ a ${displaystyle z=d}$. Suponemos que los transportistas no tienen potencial dentro del pozo y potencial de ${displaystyle V_{0}$ en las regiones de barrera.

La ecuación de Schrodinger para portadores dentro del pozo no cambia en comparación con el modelo de pozo infinito, excepto por las condiciones de contorno en las paredes, que ahora exigen que las funciones de onda y sus pendientes sean continuas en los límites.

Dentro de la región de la barrera, la ecuación de Schrodinger para los transportistas dice:

${displaystyle - ¿Qué? ¿Qué? z^{2}}+V_{0}psi (z)=Epsi (z)}$

Donde ${displaystyle #$ es la masa efectiva del transportista en la región de barrera, que generalmente difiere de su masa efectiva dentro del pozo.

Soluciones y niveles de energía

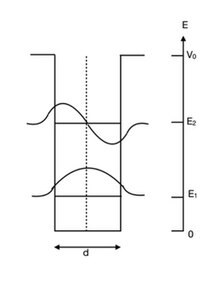
Utilizando las condiciones de límites relevantes y la condición de que la función de onda debe ser continua en el borde del pozo, obtenemos soluciones para el vector de onda ${displaystyle k}$ que satisfacen las siguientes ecuaciones trascendentales:

${displaystyle tan left({frac {k_{n}d}{2}right)={frac {m_{w}kappa } {m_{b} {fn}quad {text{(even)}}}$

y

${displaystyle tan left({frac {k_{n}d}{2}right)=-{frac {fn}fn} {fn}fn}fn}fn}fnh}}}}}}$

Donde ${displaystyle kappa }$ es la constante de decaimiento exponencial en la región de barrera, que es una medida de lo rápido que la función de onda se descompone a cero en la región de barrera. Los eigentales de energía cuantificados dentro del pozo, que dependen del vector de onda y del número cuántico (${displaystyle n}$) se dan por:

${displaystyle E_{n}={frac {hbar ^{2}k_{2}} {2m_{*}}}} {fnK}} {cHFF}} {fn}}} {fn0}}} {fn0}} {fnK}}}}}} {fn0}}}} {fn0}}}}}}}}}}}}} {\hbar}}}}}}}}}}} {\\hbar}}}}}} {\\\\\hbar}} {hbar }$

La constante de decadencia exponencial ${displaystyle kappa }$ es dado por:

${displaystyle kappa ={frac {cHFF} {2m_{b} {} {fn}}} {fn}}}}} {hbar}}}} {fn}} {fn}}}}}} {fn}}}} {fn}}} {fn}}}$

Depende del eigenstat de un portaaviones ${displaystyle E.$, la profundidad del pozo ${displaystyle V_{0}$, y la masa efectiva del transportista dentro de la región de barrera, ${displaystyle #$.

Las soluciones a las ecuaciones trascendentales anteriores se pueden encontrar fácilmente utilizando métodos numéricos o gráficos. Generalmente existen sólo unas pocas soluciones. Sin embargo, siempre habrá al menos una solución, es decir, un estado ligado en el pozo, independientemente de cuán pequeño sea el potencial. Al igual que en el pozo infinito, las funciones de onda en el pozo son de tipo sinusoidal pero decaen exponencialmente en la barrera del pozo. Esto tiene el efecto de reducir los estados de energía ligados del pozo cuántico en comparación con el pozo infinito.

Superredes

Una superred es una heteroestructura periódica hecha de materiales alternos con diferentes bandas prohibidas. El espesor de estas capas periódicas es generalmente del orden de unos pocos nanómetros. La estructura de bandas que resulta de tal configuración es una serie periódica de pozos cuánticos. Es importante que estas barreras sean lo suficientemente delgadas como para que los transportadores puedan atravesar las regiones de barrera de los múltiples pozos. Una propiedad definitoria de las superredes es que las barreras entre los pozos son lo suficientemente delgadas como para que los pozos adyacentes se acoplen. Las estructuras periódicas formadas por pozos cuánticos repetidos que tienen barreras que son demasiado gruesas para que se acoplen funciones de onda adyacentes se denominan estructuras de pozos cuánticos múltiples (MQW).

Dado que los portadores pueden atravesar las regiones de barrera entre los pozos, las funciones de onda de los pozos vecinos se acoplan a través de la barrera delgada, por lo tanto, los estados electrónicos en las superredes forman minibandas deslocalizadas. Las soluciones para los estados de energía permitidos en las superredes son similares a las de los pozos cuánticos finitos, con un cambio en las condiciones de contorno que surgen debido a la periodicidad de las estructuras. Dado que el potencial es periódico, el sistema se puede describir matemáticamente de forma similar a una red cristalina unidimensional.

Aplicaciones

Debido a su naturaleza casi bidimensional, los electrones en los pozos cuánticos tienen una densidad de estados en función de la energía que tiene distintos pasos, a diferencia de una suave dependencia de raíz cuadrada que se encuentra en los materiales a granel. Además, la masa efectiva de los huecos en la banda de valencia cambia para que coincida más con la de los electrones en la banda de valencia. Estos dos factores, junto con la reducida cantidad de material activo en los pozos cuánticos, conducen a un mejor rendimiento en dispositivos ópticos como los diodos láser. Como resultado, los pozos cuánticos se utilizan ampliamente en láseres de diodo, incluidos láseres rojos para DVD y punteros láser, láseres infrarrojos en transmisores de fibra óptica o láseres azules. También se utilizan para fabricar HEMT (transistores de alta movilidad de electrones), que se utilizan en electrónica de bajo ruido. Los fotodetectores infrarrojos de pozo cuántico también se basan en pozos cuánticos y se utilizan para obtener imágenes infrarrojas.

Al dopar el pozo mismo o, preferiblemente, la barrera de un pozo cuántico con impurezas del donante, se puede formar un gas de electrones bidimensional (2DEG). Esta estructura crea el canal conductor de un HEMT y tiene propiedades interesantes a baja temperatura. Una de esas características es el efecto Hall cuántico, que se observa en campos magnéticos elevados. Los dopantes aceptores también pueden dar lugar a un gas hueco bidimensional (2DHG).

Absorbedor saturable

Un pozo cuántico se puede fabricar como un absorbente saturable utilizando su propiedad de absorción saturable. Los absorbentes saturables se utilizan ampliamente en láseres de bloqueo en modo pasivo. Los absorbentes semiconductores saturables (SESAM) se utilizaron para el bloqueo de modo del láser ya en 1974, cuando se utilizó germanio tipo p para bloquear el modo de un láser de CO2 que generaba pulsos de aproximadamente 500 ps. Los SESAM modernos son pozos cuánticos únicos (SQW) de semiconductores III-V o pozos cuánticos múltiples (MQW) cultivados en reflectores de Bragg distribuidos por semiconductores (DBR). Inicialmente se utilizaron en un esquema de modelo de pulso resonante (RPM) como mecanismos de arranque para láseres de Ti:zafiro que empleaban KLM como un absorbente rápido saturable. RPM es otra técnica de bloqueo de modo de cavidad acoplada. A diferencia de los láseres APM que emplean no linealidad de fase de tipo Kerr no resonante para acortar el pulso, el RPM emplea la no linealidad de amplitud proporcionada por los efectos de llenado de banda resonante de los semiconductores. Los SESAM pronto se convirtieron en dispositivos absorbentes saturables intracavidad debido a su simplicidad más inherente con esta estructura. Desde entonces, el uso de SESAM ha permitido mejorar en varios órdenes de magnitud la duración de los impulsos, las potencias medias, las energías de los impulsos y las tasas de repetición de los láseres de estado sólido ultrarrápidos. Se obtuvo una potencia media de 60 W y una tasa de repetición de hasta 160 GHz. Utilizando KLM asistido por SESAM, se lograron pulsos inferiores a 6 fs directamente desde un oscilador de Ti:zafiro. Una ventaja importante que tienen los SESAM sobre otras técnicas de absorbentes saturables es que los parámetros del absorbente se pueden controlar fácilmente en una amplia gama de valores. Por ejemplo, la fluencia de saturación se puede controlar variando la reflectividad del reflector superior mientras La profundidad de modulación y el tiempo de recuperación se pueden adaptar cambiando las condiciones de crecimiento a baja temperatura para las capas absorbentes. Esta libertad de diseño ha ampliado aún más la aplicación de SESAM al bloqueo de modo de láseres de fibra, donde se necesita una profundidad de modulación relativamente alta para garantizar el arranque automático y la estabilidad operativa. Se demostraron con éxito los láseres de fibra que funcionan a ~1 μm y 1,5 μm.

Termoeléctrica

Los pozos cuánticos se han mostrado prometedores para la recolección de energía como dispositivos termoeléctricos. Se afirma que son más fáciles de fabricar y ofrecen la posibilidad de funcionar a temperatura ambiente. Los pozos conectan una cavidad central a dos depósitos electrónicos. La cavidad central se mantiene a una temperatura más alta que los depósitos. Los pozos actúan como filtros que dejan pasar electrones de determinadas energías. En general, mayores diferencias de temperatura entre la cavidad y los depósitos aumentan el flujo de electrones y la potencia de salida.

Un dispositivo experimental entregó una potencia de salida de aproximadamente 0,18 W/cm² para una diferencia de temperatura de 1 K, casi el doble de la potencia de un recolector de energía de puntos cuánticos. Los grados adicionales de libertad permitieron corrientes más grandes. Su eficiencia es ligeramente menor que la de los recolectores de energía de puntos cuánticos. Los pozos cuánticos transmiten electrones de cualquier energía por encima de un cierto nivel, mientras que los puntos cuánticos solo transmiten electrones de una energía específica.

Una posible aplicación es convertir el calor de residuos de circuitos eléctricos, por ejemplo, en chips de computadora, de vuelta a la electricidad, reduciendo la necesidad de refrigeración y energía para alimentar el chip.

Células solares

Se han propuesto pozos cuánticos para aumentar la eficiencia de las células solares. La eficiencia máxima teórica de las celdas tradicionales de unión simple es de aproximadamente el 34%, debido en gran parte a su incapacidad para capturar muchas longitudes de onda de luz diferentes. Las células solares de uniones múltiples, que constan de múltiples uniones p-n de diferentes bandas prohibidas conectadas en serie, aumentan la eficiencia teórica al ampliar el rango de longitudes de onda absorbidas, pero su complejidad y costo de fabricación limitan su uso a aplicaciones específicas. Por otro lado, las células que constan de una unión p-i-n en la que la región intrínseca contiene uno o más pozos cuánticos, conducen a un aumento de la fotocorriente sobre la corriente oscura, lo que resulta en un aumento neto de la eficiencia con respecto a las células p-n convencionales. Los fotones de energía dentro de la profundidad del pozo son absorbidos en los pozos y generan pares electrón-hueco. En condiciones de temperatura ambiente, estos portadores fotogenerados tienen suficiente energía térmica para escapar del pozo más rápido que la tasa de recombinación. Se pueden fabricar células solares de pozo cuántico de uniones múltiples elaboradas utilizando técnicas de deposición capa por capa, como la epitaxia de haz molecular o la deposición química de vapor. También se ha demostrado que las nanopartículas metálicas o dieléctricas agregadas sobre la celda conducen a aumentos adicionales en la fotoabsorción al dispersar la luz incidente en rutas de propagación laterales confinadas dentro de la capa intrínseca de múltiples pozos cuánticos.

Células solares de unión simple

Con las células solares fotovoltaicas de unión simple convencionales, la energía que generan es el producto de la fotocorriente y el voltaje a través del diodo. Como los semiconductores solo absorben fotones con energías superiores a su banda prohibida, el material de banda prohibida más pequeña absorbe una mayor parte del espectro radiativo del sol, lo que genera una corriente mayor. El voltaje de circuito abierto más alto que se puede lograr es la banda prohibida incorporada del material. Debido a que la banda prohibida del semiconductor determina tanto la corriente como el voltaje, diseñar una célula solar es siempre una solución de compromiso entre maximizar la salida de corriente con una banda prohibida baja y la salida de voltaje con una banda prohibida alta. Se ha determinado que el límite máximo teórico de eficiencia para las células solares convencionales es sólo del 31%, y los mejores dispositivos de silicio alcanzan un límite óptimo del 25%.

Con la introducción de los pozos cuánticos (QW), el límite de eficiencia de los dispositivos de silicio QW tensados de unión simple ha aumentado al 28,3 %. El aumento se debe a que la banda prohibida del material de barrera determina el voltaje incorporado. Mientras que la banda prohibida de los QW es ahora lo que determina el límite de absorción. Con sus experimentos con fotodiodos de unión pin, el grupo de Barnham demostró que colocar QW en la región agotada aumenta la eficiencia de un dispositivo. Los investigadores infieren que el aumento resultante indica que la generación de nuevos portadores y fotocorriente debido a la inclusión de energías más bajas en el espectro de absorción compensa la caída en el voltaje terminal resultante de la recombinación de portadores atrapados en los pozos cuánticos. Otros estudios han podido concluir que el aumento de la fotocorriente está directamente relacionado con el corrimiento al rojo del espectro de absorción.

Células solares multiunión

Hoy en día, entre las células solares que no son QW, las células solares de unión múltiple III/V son las más eficientes, registrando una eficiencia máxima del 46% bajo altas concentraciones de luz solar. Las células solares de uniones múltiples se crean apilando múltiples uniones pin de diferentes bandas prohibidas. La eficiencia de la célula solar aumenta con la inclusión de más radiación solar en el espectro de absorción mediante la introducción de más QW de diferentes bandas prohibidas. La relación directa entre la banda prohibida y la constante de red dificulta el avance de las células solares de uniones múltiples. A medida que se crecen juntos más pozos cuánticos (QW), el material crece con dislocaciones debido a las variables constantes de la red. Las dislocaciones reducen la duración de la difusión y la vida útil del portador. Por lo tanto, las QW proporcionan un enfoque alternativo a las células solares de uniones múltiples con una dislocación mínima de los cristales.

Energía de banda prohibida

Los investigadores buscan utilizar QW para cultivar material de alta calidad con dislocaciones mínimas de cristales y aumentar la eficiencia de la absorción de luz y la recolección de portadores para lograr células solares QW de mayor eficiencia. La sintonización de banda prohibida ayuda a los investigadores a diseñar sus células solares. Podemos estimar la banda prohibida efectiva en función de la energía de banda prohibida del QW y el cambio en la energía de banda prohibida debido a la tensión estérica: el efecto Stark de confinamiento cuántico (QCSE) y el efecto de tamaño cuántico (QSE).

${displaystyle ¿Qué? Delta E_{G}{text{Strain}+ Delta E. Delta E_{G} {text{QCSE}}$

La tensión del material causa dos efectos a la energía del bandgap. Primero es el cambio de energía relativa de la banda de conducción y valence. Este cambio energético se ve afectado por la tensión, ${displaystyle epsilon }$, coeficientes de rigidez elástica, ${displaystyle C_{11}$ y ${displaystyle C_{12}$, y potencial de deformación hidrostática, ${displaystyle a}$.

${displaystyle Delta E=-2aleft({frac ¿Qué?$

Segundo, debido a la tensión, hay una división de la degeneración de agujeros pesados y de agujeros ligeros. En un material fuertemente comprimido, los agujeros pesados (h) moverse a un estado de energía superior. En material insecticida, agujeros ligeros (lh) moverse a un estado de energía superior. Uno puede calcular la diferencia de energía debido a la división de h y lh del potencial de deformación, ${displaystyle b}$, tensión, ${displaystyle epsilon }$, y coeficientes de rigidez elástica, ${displaystyle C_{11}$ y ${displaystyle C_{12}$.

${displaystyle Delta E_{hh}=bleft({frac {C_{11}+2C_{12} {C_{11}}derecha)epsilon }$

${displaystyle Delta E_{lh}=-bleft({frac {C_{11}+2C_{12} {C_{11}}derecha)epsilon }$

El confinamiento cuántico El efecto Stark induce un cambio dependiente de la enfermedad en el bandgap. Si ${displaystyle q}$ es la carga elemental; ${displaystyle L_{text{eff,CB}}$ y ${displaystyle L_{text{eff,VB}}$ son el ancho efectivo de QWs en la banda de conducción y valence, respectivamente; ${displaystyle F}$ es el campo eléctrico inducido debido a la polarización piezoeléctrica y espontánea; y ${displaystyle hbar }$ es la constante del Planck reducido, entonces el cambio de energía es:

${displaystyle Delta E_{G} {text{QCSE}}=left({frac {15-pi ^{2}{24pi ^{2}}}}right)left({fracfrac {m_{e}{*}L_{text{eff,CB}}{4}+m_{h}{*}L_{text{eff,VB}}}{4}{4}{hbar} {i} {fnh}} {fnh}} {f}}}}}}}}} {f} {f}}}}}} {f}}}} {f}}}}}}} {f}}}}}}}} {f} {f}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}} {f} {f} {f} {f}} {f}f}}}}f}f}f}f}f}f}f}}}}}f}f}f}f}f}f}f}f}f ¿Qué?$

El efecto de tamaño cuántico (QSE) es la discretización de energía que sufre un transportista de carga debido al confinamiento cuando su El radio Bohr es mayor que el tamaño del pozo. A medida que aumenta el espesor del pozo cuántico, los QSE disminuyen. La disminución de QSE causa la ${displaystyle n=1}$ estado para bajar y disminuir el bandgap efectivo. El modelo Kronig-Penney se utiliza para calcular los estados cuánticos, y la regla de Anderson se aplica para estimar la banda de conducción y compensaciones de banda de valence en energía.

Captura y duración del operador

Con el uso eficaz de portadores en las QW, los investigadores pueden aumentar la eficiencia de las células solares de pozo cuántico (QWSC). Dentro de las QW en la región intrínseca de las células solares p-i-n, los portadores generados ópticamente son recolectados por el campo incorporado o se pierden debido a la recombinación de portadores. La recombinación de portadores es el proceso en el que un hueco y un electrón se recombinan para cancelar sus cargas. Los portadores pueden recogerse mediante la deriva del campo eléctrico. Se pueden utilizar pozos delgados y transportadores mediante emisión termoiónica o barreras delgadas y transportadores mediante túneles.

La vida útil del portador para el escape está determinada por la vida útil de los túneles y las emisiones termoiónicas. La vida útil de los túneles y de las emisiones termoiónicas depende de que la barrera tenga una altura efectiva baja. Se expresan mediante las siguientes ecuaciones:

${displaystyle {frac {fnMicrosoft Sans Serif}}={frac {npi hbar } {2t_{2}m_{} {}e^{fc} {-2}{hbar }in ¿Qué? {2m_{b} {fnMicrosoft Sans Serif}},dz}$

${displaystyle {frac {1}{text{therm}}={frac {1}{t_{w} {f} {f}} {f}} {f}} {f}} {f}}} {f}}}} {f}}} {f}}}}} {f}}}} {f}}}}} {f}}}}}} {f}}}} {f}}}}}}} {f}}}}}}}}}}} {f}}}}}}} {f} {f}}} {f}}}}} {f}}} {f}}}}}} {f}}}}}}}}}}}}}}}}}}}}} {f}}} {f}}}}}} {f}}} {f}}}}}}}}}} {f}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}} { {fnK}{2pi} ¿Qué? {E_{b} {KT}}}$,

Donde ${displaystyle #$ y ${displaystyle ¿Qué?$ son efectivas masas de portadores de carga en la barrera y bien, ${displaystyle E_{b}$ es la altura de barrera efectiva, y ${displaystyle E(z)}$ es el campo eléctrico.

Entonces se puede calcular la vida útil de escape de la siguiente manera:

${displaystyle {frac {1}{text{esc}}={frac {1}{tau ¿Qué? {1}{tau _{text{therm}}}}}$

La probabilidad total de que los transportistas minoritarios escapen de QWs es una suma de la probabilidad de cada pozo,

${displaystyle P_{text{tot}=P_{i} {N}$.

Aquí, ${displaystyle ¿Qué? ¿Qué? {1} {tau _{text{rec}}}}}}$, donde ${displaystyle tau _{text{rec}}}$ es vida de recombinación, y ${displaystyle N}$ es el número total de QW en la región intrínseca.

Para ${displaystyle tau _{text{esc.}lltau _{rec}$, hay una alta probabilidad para el recogimiento del transportista. Las asunciones hechas en este método de modelado son que cada portador cruza ${displaystyle N}$ QWs, mientras que, en realidad, cruzan diferentes números de QWs y que una captura de portador es al 100%, que puede no ser verdad en condiciones de dopaje de fondo alto.

Por ejemplo, tomar En_0.18Ga_0,82As (125${displaystyle mathrm {AA}$)/GaAs_0.36P_0,644 (40)${displaystyle mathrm {AA}$) en la consideración, el túnel y la vida útil de las emisiones termiónicas son 0.89 y 1.84, respectivamente. Incluso si se asume un tiempo de recombinación de 50ns, la probabilidad de escape de un pozo cuántico único y 100 pozos cuánticos es 0.984 y 0.1686, lo que no es suficiente para una captura eficiente del portador. Reducir el espesor de la barrera a 20 ångstroms reduce ${displaystyle tau _{text{tun.}}}$ a 4.1276 ps, aumentando la probabilidad de escape de más de 100 QWs a 0.9918. Indicando que el uso de barriers delgados es esencial para una colección de portadores más eficiente.

Sostenibilidad de los dispositivos de pozos cuánticos en comparación con el material a granel en términos de rendimiento

En el rango de 1,1-1,3 eV, Sayed et al. compara la eficiencia cuántica externa (EQE) de una subcelda metamórfica de InGaAs sobre sustratos de Ge de Spectrolab con una de 100 períodos In_0,30Ga_0,70As(3,5 nm)/GaAs(2,7 nm)/ GaAs_0,60P_0,40(3,0 nm) QWSC de Fuji et al. El material a granel muestra valores de EQE más altos que los de QW en la región de 880-900 nm, mientras que los QW tienen valores de EQE más altos en el rango de 400-600 nm. Este resultado proporciona cierta evidencia de que existe una lucha por extender las QW. umbrales de absorción a longitudes de onda más largas debido al equilibrio de tensión y problemas de transporte del portador. Sin embargo, el material a granel tiene más deformaciones, lo que lleva a una vida útil más corta de los soportes minoritarios.

En el rango de 1,6-1,8 eV, los AlGaAs de red emparejada de Heckelman et al. e InGaAsP de Jain et al. Sayed los compara con la estructura InGaAsP / InGaP QW de celosía emparejada de Sayed et al. Al igual que el rango de 1,1-1,3 eV, la EQE del material a granel es mayor en la región de longitud de onda más larga del espectro, pero los QW son ventajosos en el sentido de que absorben una región más amplia del espectro. Además, se pueden cultivar a temperaturas más bajas evitando la degradación térmica.

La aplicación de pozos cuánticos en muchos dispositivos es una solución viable para aumentar la eficiencia energética de dichos dispositivos. En el caso del láser, la mejora ya ha dado lugar a resultados significativos, como en el caso del LED. Con las QWSC, la recolección de energía del sol se convierte en un método más potente de cultivar energía al poder absorber más radiación solar y al poder capturar dicha energía de los portadores de carga de manera más eficiente. Una opción viable como las QWSC brinda al público la oportunidad de alejarse de los métodos que inducen gases de efecto invernadero y adoptar una alternativa más ecológica: la energía solar.