Potencial eléctrico

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Línea integral del campo eléctrico

El potencial eléctrico (también llamado potencial de campo eléctrico, caída de potencial, potencial electrostático) se define como la cantidad de energía de trabajo necesaria para mover una unidad de carga eléctrica desde un punto de referencia hasta el punto específico en un campo eléctrico. Más precisamente, es la energía por unidad de carga para una carga de prueba que es tan pequeña que la perturbación del campo bajo consideración es insignificante. Además, se supone que el movimiento a través del campo procede con una aceleración despreciable, para evitar que la carga de prueba adquiera energía cinética o produzca radiación. Por definición, el potencial eléctrico en el punto de referencia es cero unidades. Normalmente, el punto de referencia es la tierra o un punto en el infinito, aunque se puede utilizar cualquier punto.

En la electrostática clásica, el campo electrostático es una cantidad vectorial expresada como el gradiente del potencial electrostático, que es una cantidad escalar denotada por $V$ u ocasionalmente $φ$ , igual a la energía potencial eléctrica de cualquier partícula cargada en cualquier ubicación (medida en joules) dividida por la carga de esa partícula (medida en culombios). Al dividir la carga de la partícula se obtiene un cociente que es una propiedad del propio campo eléctrico. En resumen, un potencial eléctrico es la energía potencial eléctrica por unidad de carga.

Este valor se puede calcular en un campo eléctrico estático (invariable en el tiempo) o dinámico (variable en el tiempo) en un momento específico con la unidad julios por coulomb (J⋅C⁻¹) o voltios (V). Se supone que el potencial eléctrico en el infinito es cero.

En electrodinámica, cuando hay campos variables en el tiempo, el campo eléctrico no se puede expresar solo en términos de un potencial escalar. En cambio, el campo eléctrico se puede expresar en términos tanto del potencial eléctrico escalar como del potencial del vector magnético. El potencial eléctrico y el vector potencial magnético juntos forman un cuatro vector, de modo que los dos tipos de potencial se mezclan bajo las transformaciones de Lorentz.

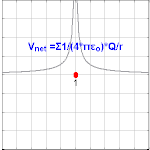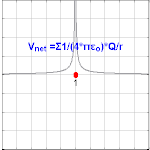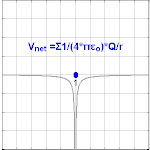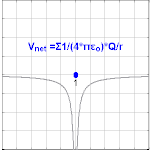
Prácticamente, el potencial eléctrico es una función continua en todo el espacio, porque una derivada espacial de un potencial eléctrico discontinuo produce un campo eléctrico de una magnitud imposiblemente infinita. En particular, el potencial eléctrico debido a una carga puntual idealizada (proporcional a $1 ⁄ r$ , con $r$ la distancia desde la carga puntual) es continua en todo el espacio excepto en la ubicación de la carga puntual. Aunque el campo eléctrico no es continuo a través de una carga superficial idealizada, no es infinito en ningún punto. Por lo tanto, el potencial eléctrico es continuo a través de una carga superficial idealizada. Además, una línea de carga idealizada tiene un potencial eléctrico (proporcional a $ln(r)$ , con $r$ la distancia radial desde la línea de carga) es continua en todas partes excepto en la línea de carga.

Introducción

La mecánica clásica explora conceptos como fuerza, energía y potencial. La fuerza y la energía potencial están directamente relacionadas. Una fuerza neta que actúa sobre cualquier objeto hará que se acelere. A medida que un objeto se mueve en la dirección de una fuerza que actúa sobre él, su energía potencial disminuye. Por ejemplo, la energía potencial gravitatoria de una bala de cañón en la cima de una colina es mayor que en la base de la colina. A medida que rueda cuesta abajo, su energía potencial disminuye y se traduce en movimiento: energía cinética.

Es posible definir el potencial de ciertos campos de fuerza de modo que la energía potencial de un objeto en ese campo dependa únicamente de la posición del objeto con respecto al campo. Dos de estos campos de fuerza son un campo gravitatorio y un campo eléctrico (en ausencia de campos magnéticos variables en el tiempo). Dichos campos afectan a los objetos debido a las propiedades intrínsecas (p. ej., masa o carga) y las posiciones de los objetos.

Un objeto puede poseer una propiedad conocida como carga eléctrica. Dado que un campo eléctrico ejerce una fuerza sobre un objeto cargado, si el objeto tiene una carga positiva, la fuerza estará en la dirección del vector del campo eléctrico en la ubicación de la carga; si la carga es negativa, la fuerza será en dirección opuesta.

La magnitud de la fuerza viene dada por la cantidad de la carga multiplicada por la magnitud del vector del campo eléctrico,

{displaystyle |mathbf {F} |=q|mathbf {E} |.}

Electrostática

Potencia eléctrica de los cargos por puntos positivos y negativos separados mostrados como rango de color de magenta (+), a través de amarillo (0), a cyan (−). Los contornos circulares son líneas de equipo. Las líneas de campo eléctrico dejan la carga positiva e introducen la carga negativa.

Potencia eléctrica en las proximidades de dos cargos opuestos.

El potencial eléctrico en un punto $r$ en un campo eléctrico estático $E$ viene dada por la integral de línea

${displaystyle V_{mathbf {E} }=-int _{mathcal {C}}mathbf {E} cdot mathrm {d} {boldsymbol {ell }},}$

Donde $C$ es un camino arbitrario desde algún punto de referencia fijo a $r$ . En electrostáticos, la ecuación Maxwell-Faraday revela que el rizo ${textstyle nabla times mathbf {E} }$ es cero, haciendo el campo eléctrico conservador. Así, la línea integral arriba no depende del camino específico $C$ elegido pero sólo en sus puntos finales, haciendo ${textstyle V_{mathbf {E} }}$ bien definido en todas partes. El teorema gradiente nos permite escribir:

${displaystyle mathbf {E} =-mathbf {nabla } V_{mathbf {E} },}$

Esto establece que el campo eléctrico apunta "cuesta abajo" hacia voltajes más bajos. Por la ley de Gauss, también se puede encontrar el potencial para satisfacer la ecuación de Poisson:

{displaystyle mathbf {nabla } cdot mathbf {E} =mathbf {nabla } cdot left(-mathbf {nabla } V_{mathbf {E} }right)=-nabla ^{2}V_{mathbf {E} }=rho /varepsilon _{0}}

Donde $***$ es la densidad total de carga y ${textstyle mathbf {nabla } cdot }$ denota la divergencia.

El concepto de potencial eléctrico está estrechamente relacionado con el de energía potencial. Una carga de prueba, $q$ , tiene una energía potencial eléctrica, $U E$ , dada por

{displaystyle U_{mathbf {E} }=q,V.}

La energía potencial y, por lo tanto, también el potencial eléctrico, solo se define hasta una constante aditiva: uno debe elegir arbitrariamente una posición donde la energía potencial y el potencial eléctrico sean cero.

Estas ecuaciones no se pueden utilizar si ${textstyle nabla times mathbf {E} neq mathbf {0} }$ , es decir, en el caso de un campo eléctrico no conservador (causado por un campo magnético cambiante; vea las ecuaciones de Maxwell). La generalización del potencial eléctrico a este caso se describe en la sección § Generalización a electrodinámica.

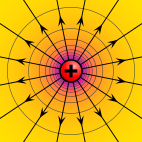
Potencial eléctrico debido a una carga puntual

El potencial eléctrico creado por una carga, Q, es V=Q/(4πε₀r). Diferentes valores de Q rendimiento diferentes valores de potencial eléctrico, V, (shown in the image).

El potencial eléctrico que surge de una carga puntual, $Q$ , a una distancia, $r$ , desde la ubicación de $Q$ se observa que es

{displaystyle V_{mathbf {E} }={frac {1}{4pi varepsilon _{0}}}{frac {Q}{r}},}

ε 0

V E

Potencial de la bomba

{displaystyle k_{e}={frac {1}{4pi varepsilon _{0}}}}

se conoce como la constante de Coulomb.

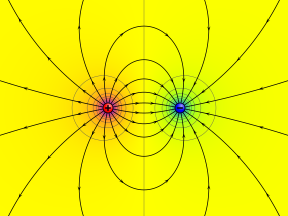
El potencial eléctrico en cualquier lugar, ${textstyle {textbf {r}}}$ , en un sistema de cargos de punto es igual a la suma de los potenciales eléctricos individuales debido a cada cargo de punto en el sistema. Este hecho simplifica significativamente los cálculos, ya que la adición de campos potenciales (calar) es mucho más fácil que la adición de los campos eléctricos (vector). Específicamente, el potencial de un conjunto de cargos discretos $q i$ en puntos $r i$ se convierte en

{displaystyle V_{mathbf {E} }(mathbf {r})=k_{e}sum _{i}{frac {q_{i}}{|mathbf {r} -mathbf {r} _{i}|}},}

${displaystyle mathbf {r} }$ es un punto en el que se evalúa el potencial.
${displaystyle mathbf {r} _{i}}$ es un punto en el que hay un cargo no cero.
${displaystyle q_{i}}$ es la carga en el punto ${displaystyle mathbf {r} _{i}}$ .

y el potencial de una distribución de carga continua $ρ (r)$ se vuelve

{displaystyle V_{mathbf {E} }(mathbf {r})=k_{e}int _{R}{frac {rho (mathbf {r} ')}{|mathbf {r} -mathbf {r} '|}}d^{3}r'.}

${displaystyle mathbf {r} }$ es un punto en el que se evalúa el potencial.
${displaystyle R}$ es una región que contiene todos los puntos en los que la densidad de carga no es cero.
${displaystyle mathbf {r} '}$ es un punto dentro ${displaystyle R}$ .
${displaystyle rho (mathbf {r} ')}$ es la densidad de carga en el punto ${displaystyle mathbf {r} '}$ .

Las ecuaciones dadas anteriormente para el potencial eléctrico (y todas las ecuaciones utilizadas aquí) están en las formas requeridas por las unidades SI. En algunos otros sistemas de unidades (menos comunes), como CGS-Gaussian, muchas de estas ecuaciones estarían alteradas.

Generalización a la electrodinámica

Cuando los campos magnéticos que van en el tiempo están presentes (que es cierto cuando hay campos eléctricos que van en el tiempo y viceversa), no es posible describir el campo eléctrico simplemente en términos de un potencial de escalar $V$ porque el campo eléctrico ya no es conservador: $textstyleint_C mathbf{E}cdot mathrm{d}boldsymbol{ell}$ es dependiente del camino porque $mathbf{nabla} times mathbf{E} neq mathbf{0}$ (debido a la ecuación Maxwell-Faraday).

En cambio, todavía se puede definir un potencial escalar incluyendo también el potencial del vector magnético $A$ . En particular, $A$ se define para satisfacer:

{displaystyle mathbf {B} =mathbf {nabla } times mathbf {A} }

donde $B$ es el campo magnético. Por el teorema fundamental del cálculo vectorial, siempre se puede encontrar tal $A$ , ya que la divergencia del campo magnético es siempre cero debido a la ausencia de monopolos magnéticos. Ahora, la cantidad

mathbf{F} = mathbf{E} + frac{partialmathbf{A}}{partial t}

es un campo conservador, desde el rizo de $mathbf {E}$ es cancelado por el rizo de ${displaystyle {frac {partial mathbf {A} }{partial t}}}$ según la ecuación Maxwell-Faraday. Por lo tanto, uno puede escribir

{displaystyle mathbf {E} =-mathbf {nabla } V-{frac {partial mathbf {A} }{partial t}},}

donde $V$ es el potencial escalar definido por el campo conservativo $F .$

El potencial electrostático es simplemente el caso especial de esta definición donde $A$ es invariable en el tiempo. Por otro lado, para campos variantes en el tiempo,

{displaystyle -int _{a}^{b}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}neq V_{(b)}-V_{(a)}}

a diferencia de la electrostática.

Libertad de calibre

El potencial electrostático podría tener cualquier constante agregado a él sin afectar el campo eléctrico. En electrodinámica, el potencial eléctrico tiene infinitamente muchos grados de libertad. Para cualquier campo de escalar (posiblemente de tiempo o de invasión espacial), $psi$ , podemos realizar la siguiente transformación del medidor para encontrar un nuevo conjunto de potenciales que producen exactamente los mismos campos eléctricos y magnéticos:

{displaystyle V^{prime }=V-{frac {partial psi }{partial t}}}

{displaystyle mathbf {A} ^{prime }=mathbf {A} +nabla psi }

Dadas las diferentes opciones de calibre, el potencial eléctrico podría tener propiedades bastante diferentes. En el calibre de Coulomb, el potencial eléctrico viene dado por la ecuación de Poisson

{displaystyle nabla ^{2}V=-{frac {rho }{varepsilon _{0}}}}

igual que en la electrostática. Sin embargo, en el calibre de Lorenz, el potencial eléctrico es un potencial retardado que se propaga a la velocidad de la luz y es la solución a una ecuación de onda no homogénea:

{displaystyle nabla ^{2}V-{frac {1}{c^{2}}}{frac {partial ^{2}V}{partial t^{2}}}=-{frac {rho }{varepsilon _{0}}}}

Unidades

La unidad de potencial eléctrico derivada del SI es el voltio (en honor a Alessandro Volta), denotada como V, razón por la cual la diferencia de potencial eléctrico entre dos puntos en el espacio se conoce como voltaje. Las unidades más antiguas rara vez se utilizan en la actualidad. Las variantes del sistema de unidades centímetro-gramo-segundo incluían varias unidades diferentes para el potencial eléctrico, incluido el abvolt y el statvolt.

Potencial de Galvani frente a potencial electroquímico

Dentro de los metales (y otros sólidos y líquidos), la energía de un electrón se ve afectada no sólo por el potencial eléctrico, sino también por el entorno atómico específico en el que se encuentra. Cuando un voltímetro está conectado entre dos tipos diferentes de metal, mide el diferencia potencial corregido para los diferentes ambientes atómicos. La cantidad medida por un voltímetro se llama potencial electroquímico o nivel fermi, mientras que el potencial eléctrico sin ajustar puro, $V$ , a veces se llama el potencial de Galvani, $phi$ . Los términos "voltaje" y "poder eléctrico" son un poco ambiguos pero uno puede referirse a o de estos en diferentes contextos.

Contenido relacionado

Más resultados...