Potencial de reposo
Un potencial de membrana relativamente estático que generalmente se conoce como el valor del suelo para el voltaje trans-membrana.
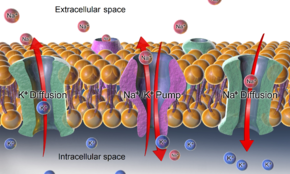
El potencial de membrana relativamente estático de las células inactivas se denomina potencial de membrana en reposo (o voltaje en reposo), a diferencia de los fenómenos electroquímicos dinámicos específicos llamados potencial de acción y potencial de membrana graduado.
Aparte de los dos últimos, que ocurren en las células excitables (neuronas, músculos y algunas células secretoras de las glándulas), el voltaje de la membrana en la mayoría de las células no excitables también puede sufrir cambios en respuesta a estímulos ambientales o intracelulares. El potencial de reposo existe debido a las diferencias en las permeabilidades de las membranas para los iones potasio, sodio, calcio y cloruro, que a su vez resultan de la actividad funcional de varios canales iónicos, transportadores e intercambiadores de iones. Convencionalmente, el potencial de membrana en reposo se puede definir como un valor fundamental relativamente estable del voltaje transmembrana en células animales y vegetales.
Debido a que la permeabilidad de la membrana para el potasio es mucho mayor que la de otros iones, y debido al fuerte gradiente químico del potasio, los iones de potasio fluyen desde el citosol hacia el espacio extracelular llevando carga positiva, hasta que su movimiento se equilibra con la acumulación. Formación de carga negativa en la superficie interna de la membrana. Nuevamente, debido a la alta permeabilidad relativa al potasio, el potencial de membrana resultante casi siempre está cerca del potencial de inversión del potasio. Pero para que este proceso se produzca, primero se debe establecer un gradiente de concentración de iones potasio. Este trabajo lo realizan las bombas/transportadores y/o intercambiadores de iones y generalmente está impulsado por ATP.
En el caso del potencial de membrana en reposo a través de la membrana plasmática de una célula animal, los gradientes de potasio (y sodio) son establecidos por la Na+/K+-ATPasa (bomba de sodio-potasio), que transporta 2 iones de potasio al interior y 3 iones de sodio al exterior a costa de 1 molécula de ATP. En otros casos, por ejemplo, se puede establecer un potencial de membrana mediante la acidificación del interior de un compartimento membranoso (como la bomba de protones que genera potencial de membrana a través de las membranas de las vesículas sinápticas).
Electroneutralidad
En la mayoría de los tratamientos cuantitativos del potencial de membrana, como la derivación de la ecuación de Goldman, se supone la electroneutralidad; es decir, que no hay un exceso de carga mensurable en ninguno de los lados de la membrana. Entonces, aunque hay un potencial eléctrico a través de la membrana debido a la separación de carga, no existe una diferencia real mensurable en la concentración global de iones positivos y negativos a través de la membrana (como se estima a continuación), es decir, no hay una diferencia real mensurable. cargue el exceso en ambos lados. Esto ocurre porque el efecto de la carga sobre el potencial electroquímico es enormemente mayor que el efecto de la concentración, por lo que un cambio indetectable en la concentración crea un gran cambio en el potencial eléctrico.
Generación del potencial de reposo
Las membranas celulares suelen ser permeables sólo a un subconjunto de iones. Estos suelen incluir iones de potasio, iones de cloruro, iones de bicarbonato y otros. Para simplificar la descripción de la base iónica del potencial de membrana en reposo, es más útil considerar al principio sólo una especie iónica y considerar las demás más adelante. Dado que los potenciales transmembrana plasmática casi siempre están determinados principalmente por la permeabilidad del potasio, ahí es por donde empezar.

- El panel 1 del diagrama muestra una representación diagramática de una célula simple donde ya se ha establecido un gradiente de concentración. Este panel se dibuja como si la membrana no tiene permeabilidad a ningún ion. No hay potencial de membrana porque a pesar de haber un gradiente de concentración para el potasio, no hay desequilibrio de carga neta en la membrana. Si la membrana fuera permeable a un tipo de iones que se concentra más en un lado de la membrana, entonces ese ión contribuiría al voltaje de la membrana porque los iones permeantes se moverían a través de la membrana con movimiento neto de ese ión hacia abajo el gradiente de concentración. Habrá movimiento neto desde el lado de la membrana con una mayor concentración del ión al lado con menor concentración. Tal movimiento de un ión a través de la membrana resultaría en un desequilibrio neto de carga a través de la membrana y un potencial de membrana. Este es un mecanismo común por el cual muchas células establecen un potencial de membrana.
- En el panel 2 del diagrama, la membrana celular se ha hecho permeable a iones de potasio, pero no a los aniones (An−En la celda. Estas aniones son mayoritariamente aportadas por proteínas. Hay energía almacenada en el gradiente de concentración de iones de potasio que se puede convertir en un gradiente eléctrico cuando potasio (K)+Los iones salen de la celda. Tenga en cuenta que los iones de potasio pueden moverse a través de la membrana en ambas direcciones, pero por el proceso puramente estadístico que surge de la mayor concentración de iones de potasio dentro de la célula, habrá más iones de potasio saliendo de la célula. Debido a que hay una mayor concentración de iones de potasio dentro de las células, su movimiento molecular aleatorio es más probable encontrar el poro permeabilidad (canal de iones) que es el caso de los iones de potasio que están fuera y a una menor concentración. Un K interno+ es simplemente "más probable" dejar la célula que un K extracelular+ es entrarlo. Es una cuestión de difusión haciendo trabajo disipando el gradiente de concentración. Cuando el potasio sale de la celda, se va detrás de los aniones. Por lo tanto, una separación de carga se desarrolla como K+ deja la celda. Esta separación de carga crea un voltaje transmembrano. Esta tensión transmembrana es el potencial de la membrana. A medida que el potasio siga dejando la célula, separando más cargas, el potencial de membrana seguirá creciendo. La longitud de las flechas (verde indicando gradiente de concentración, tensión de indicación roja), representa la magnitud del movimiento de iones de potasio debido a cada forma de energía. La dirección de la flecha indica la dirección en la que se aplica esa fuerza particular. Así, el voltaje de la membrana del edificio es una fuerza creciente que actúa contra la tendencia de movimiento neto de iones de potasio por el gradiente de concentración de potasio.
- En el Panel 3, el voltaje de la membrana ha crecido en la medida en que su "forzamiento" ahora coincide con los gradientes de concentración. Desde estas fuerzas (que se aplican a K+) son ahora la misma fuerza y orientada en direcciones opuestas, el sistema está ahora en equilibrio. De otra manera, la tendencia del potasio a salir de la célula corriendo por su gradiente de concentración se combina ahora con la tendencia del voltaje de la membrana a tirar los iones de potasio de vuelta a la célula. K+ continúa pasando por la membrana, pero la velocidad a la que entra y deja la célula es la misma, por lo tanto, no hay neto corriente de potasio. Porque el K+ está en equilibrio, el potencial de la membrana es estable o "resting" (E)K).
El voltaje en reposo es el resultado de varias enzimas translocadoras de iones (uniportadores, cotransportadores y bombas) en la membrana plasmática, que operan constantemente en paralelo, por lo que cada translocadora de iones tiene su fuerza electromotriz característica (= potencial de inversión = &# 39;voltaje de equilibrio'), dependiendo de las concentraciones de sustrato particulares dentro y fuera (ATP interno incluido en el caso de algunas bombas). La ATPasa exportadora de H+ hace que el voltaje de la membrana en plantas y hongos sea mucho más negativo que en las células animales más investigadas, donde el voltaje en reposo está determinado principalmente por canales iónicos selectivos.
En la mayoría de las neuronas, el potencial de reposo tiene un valor de aproximadamente −70 mV. El potencial de reposo está determinado principalmente por las concentraciones de iones en los fluidos a ambos lados de la membrana celular y las proteínas transportadoras de iones que se encuentran en la membrana celular. A continuación se describe cómo las concentraciones de iones y las proteínas transportadoras de membrana influyen en el valor del potencial de reposo.
El potencial de reposo de una célula se puede entender mejor si se piensa en términos de potenciales de equilibrio. En el diagrama de ejemplo aquí, a la celda modelo se le dio solo un ion permeante (potasio). En este caso, el potencial de reposo de esta célula sería el mismo que el potencial de equilibrio del potasio.
Sin embargo, una célula real es más complicada y tiene permeabilidades a muchos iones, cada uno de los cuales contribuye al potencial de reposo. Para entender mejor, consideremos una célula con sólo dos iones permeantes, potasio y sodio. Considere un caso en el que estos dos iones tienen gradientes de concentración iguales dirigidos en direcciones opuestas y las permeabilidades de la membrana a ambos iones son iguales. K+ al salir de la célula tenderá a arrastrar el potencial de membrana hacia EK. El Na+ que entra en la célula tenderá a arrastrar el potencial de membrana hacia el potencial de inversión del sodio ENa. Dado que las permeabilidades a ambos iones se establecieron iguales, el potencial de membrana, al final del tira y afloja Na+/K+, terminará a mitad de camino. entre ENa y EK. Como ENa y EK eran iguales pero de signos opuestos, el punto medio es cero, lo que significa que el La membrana descansará a 0 mV.
Tenga en cuenta que aunque el potencial de membrana en 0 mV es estable, no es una condición de equilibrio porque ninguno de los iones contribuyentes está en equilibrio. Los iones difunden sus gradientes electroquímicos a través de canales de iones, pero el potencial de la membrana es sostenido por K continua+ influx y Na+ efflux via ion transporters. Tal situación con permeabilidades similares para iones contraactores, como potasio y sodio en células animales, puede ser extremadamente costoso para la célula si estas permeabilidades son relativamente grandes, ya que se necesita mucha energía ATP para bombear los iones de vuelta. Debido a que ninguna célula real puede permitirse tales permeabilidades iónicas iguales y grandes en reposo, el potencial de reposo de las células animales se determina por la alta permeabilidad predominante al potasio y se ajusta al valor requerido mediante la modulación de permeabilidad y gradientes de sodio y cloruro.
En una célula animal sana, la permeabilidad al Na+ es aproximadamente el 5% de la permeabilidad al K+ o incluso menos, mientras que los respectivos potenciales de inversión son +60 mV para el sodio (ENa) y −80 mV para el potasio (EK). Por lo tanto, el potencial de membrana no estará justo en EK, sino que se despolarizará desde EK en una cantidad de aproximadamente el 5 % de la diferencia de 140 mV entre EK y ENa. Por tanto, el potencial de reposo de la célula será de aproximadamente −73 mV.
En una notación más formal, el potencial de membrana es el promedio ponderado del potencial de equilibrio de cada ión contribuyente. El tamaño de cada peso es la conductancia relativa de cada ion. En el caso normal, donde tres iones contribuyen al potencial de membrana:
- ,
dónde
- Em es el potencial de la membrana, medido en voltios
- EX es el potencial de equilibrio para ion X, también en voltios
- gX/gTot es la conducta relativa de ion X, que es sin dimensión
- gTot es la conducta total de todos los iones permeantes en unidades arbitrarias (por ejemplo, siemens for electric conductance), en este caso gK+ + gNa+ + gCl−
Proteínas de transporte de membrana
Para la determinación de los potenciales de membrana, los dos tipos más importantes de proteínas de transporte de iones de membrana son canales de iones y transportadores de iones. Las proteínas de canal Ion crean caminos a través de las membranas celulares a través de los cuales los iones pueden difusa pasivamente sin gasto directo de energía metabólica. Ellos tienen selectividad para ciertos iones, por lo tanto, hay potasio-, cloruro-, y canales de ion sodio-selectiva. Diferentes células e incluso diferentes partes de una célula (dendritos, cuerpos celulares, nodos de Ranvier) tendrán diferentes cantidades de varias proteínas de transporte de iones. Por lo general, la cantidad de ciertos canales de potasio es más importante para el control del potencial de reposo (ver abajo). Algunas bombas de iones como el Na+/K+-ATPase son electrogénicas, es decir, producen desequilibrio de carga en la membrana celular y también pueden contribuir directamente al potencial de la membrana. La mayoría de las bombas usan energía metabólica (ATP) para funcionar.
Potenciales de equilibrio
Para la mayoría de las células animales, los iones de potasio (K+) son los más importantes para el potencial de reposo. Debido al transporte activo de iones de potasio, la concentración de potasio es mayor dentro de las células que en el exterior. La mayoría de las células tienen proteínas de canales iónicos selectivas de potasio que permanecen abiertas todo el tiempo. Habrá un movimiento neto de iones de potasio cargados positivamente a través de estos canales de potasio con la consiguiente acumulación de un exceso de carga negativa dentro de la célula. El movimiento hacia afuera de los iones de potasio cargados positivamente se debe al movimiento molecular aleatorio (difusión) y continúa hasta que se acumula suficiente exceso de carga negativa dentro de la célula para formar un potencial de membrana que puede equilibrar la diferencia en la concentración de potasio entre el interior y el exterior de la célula. "Equilibrio" significa que la fuerza eléctrica (potencial) que resulta de la acumulación de carga iónica, y que impide la difusión hacia afuera, aumenta hasta que es igual en magnitud pero opuesta en dirección a la tendencia del movimiento difusivo hacia afuera del potasio. Este punto de equilibrio es un potencial de equilibrio ya que el flujo (o corriente) transmembrana neto de K+ es cero. Una buena aproximación del potencial de equilibrio de un ion determinado sólo necesita las concentraciones a ambos lados de la membrana y la temperatura. Se puede calcular mediante la ecuación de Nernst:
dónde
- Eeq,K+ es el potencial de equilibrio para potasio, medido en voltios
- R es la constante de gas universal, igual a 8.314 joules· K−1·mol−1
- T es la temperatura absoluta, medida en kelvins (= K = grados Celsius + 273.15)
- z es el número de cargos elementales del ión en cuestión involucrados en la reacción
- F es la constante Faraday, igual a 96.485 coulombs·mol−1 o J·V−1·mol−1
- [K+]o es la concentración extracelular de potasio, medida en mol·m−3 o mmol·l−1
- [K+]i es también la concentración intracelular de potasio
Son comunes los potenciales de equilibrio del potasio de alrededor de −80 milivoltios (dentro negativo). Se observan diferencias en diferentes especies, diferentes tejidos dentro del mismo animal y los mismos tejidos en diferentes condiciones ambientales. Aplicando la ecuación de Nernst anterior, se pueden explicar estas diferencias mediante cambios en la concentración relativa de K+ o diferencias de temperatura.
Para uso común, la ecuación de Nernst a menudo se presenta en una forma simplificada, asumiendo una temperatura típica del cuerpo humano (37 °C), reduciendo las constantes y cambiando a Log base 10. (Las unidades utilizadas para la concentración no son importantes ya que cancelarán en una proporción). Para el potasio a temperatura corporal normal, se puede calcular el potencial de equilibrio en milivoltios como:
Del mismo modo, el potencial de equilibrio del sodio (Na+) a temperatura normal del cuerpo humano se calcula utilizando la misma constante simplificada. Puede calcular E suponiendo una concentración exterior, [K+]o, de 10 mM y una concentración interior, [K+] i, de 100mM. Para los iones cloruro (Cl−) se debe invertir el signo de la constante (−61,54 mV). Si se calcula el potencial de equilibrio del calcio (Ca2+), la carga 2+ reduce a la mitad la constante simplificada a 30,77 mV. Si se trabaja a temperatura ambiente, aproximadamente 21 °C, las constantes calculadas son aproximadamente 58 mV para K+ y Na+, −58 mV para Cl− y 29 mV para Ca2+. A temperatura fisiológica, aproximadamente 29,5 °C, y concentraciones fisiológicas (que varían para cada ion), los potenciales calculados son aproximadamente 67 mV para Na+, −90 mV para K+, −86 mV para Cl− y 123 mV para Ca2+.
Potenciales en reposo
El potencial de membrana en reposo no es un potencial de equilibrio ya que depende del gasto constante de energía (para bombas iónicas como se mencionó anteriormente) para su mantenimiento. Es un potencial de difusión dinámico el que tiene en cuenta este mecanismo, totalmente diferente al potencial de equilibrio de la almohada, que es cierto sin importar la naturaleza del sistema bajo consideración. El potencial de membrana en reposo está dominado por las especies iónicas del sistema que tienen la mayor conductancia a través de la membrana. Para la mayoría de las células esto es potasio. Como el potasio también es el ion con el potencial de equilibrio más negativo, normalmente el potencial de reposo no puede ser más negativo que el potencial de equilibrio del potasio. El potencial de reposo se puede calcular con la ecuación de voltaje de Goldman-Hodgkin-Katz utilizando las concentraciones de iones como para el potencial de equilibrio y al mismo tiempo incluyendo las permeabilidades relativas de cada especie iónica. En condiciones normales, se puede suponer con seguridad que sólo los iones potasio, sodio (Na+) y cloruro (Cl−) desempeñan un papel importante en el potencial de reposo:
Esta ecuación se parece a la ecuación de Nernst, pero tiene un término para cada ion permeante. Además, se ha insertado z en la ecuación, lo que provoca que las concentraciones intracelulares y extracelulares de Cl− se inviertan en relación con K+ y Na<. sup>+, ya que la carga negativa del cloruro se maneja invirtiendo la fracción dentro del término logarítmico. *Em es el potencial de membrana, medido en voltios *R, T y F son como arriba *Ps es la permeabilidad relativa del ion s *[s]Y es la concentración de ion s en el compartimento Y como arriba. Otra forma de ver el potencial de membrana, considerando en cambio la conductancia de los canales iónicos en lugar de la permeabilidad de la membrana, es utilizar la ecuación de Millman (también llamada ecuación de conductancia de cuerdas):
o reformulado
donde gtot es la conductancia combinada de todas las especies iónicas, nuevamente en unidades arbitrarias. La última ecuación representa el potencial de membrana en reposo como un promedio ponderado de los potenciales de inversión del sistema, donde los pesos son las conductancias relativas de cada especie de ion (g X/gtot). Durante el potencial de acción, estos pesos cambian. Si las conductancias de Na+ y Cl− son cero, el potencial de membrana se reduce al potencial de Nernst para K+ (como g K+ = gtot). Normalmente, en condiciones de reposo gNa+ y gCl− no son cero, pero son mucho más pequeños que < i>gK+, lo que hace que Em esté cerca de Eeq,K+ . Condiciones médicas como la hiperpotasemia en la que se modifica el potasio sérico de la sangre (que gobierna la [K+]o) son muy peligrosas ya que compensan la E< sub>eq,K+, afectando así a Em. Esto puede causar arritmias y paro cardíaco. El uso de una inyección en bolo de cloruro de potasio en ejecuciones por inyección letal detiene el corazón al cambiar el potencial de reposo a un valor más positivo, lo que despolariza y contrae las células cardíacas de forma permanente, no permitiendo que el corazón se repolarice y, por lo tanto, entre en diástole para recargarse. con sangre.
Aunque la ecuación de voltaje GHK y la ecuación de Millman están relacionadas, no son equivalentes. La diferencia crítica es que la ecuación de Millman asume la relación de voltaje actual para ser ohmica, mientras que la ecuación de voltaje de GHK toma en consideración las pequeñas rectificaciones instantáneas predichas por la ecuación de flujo GHK causada por el gradiente de concentración de iones. Así, una estimación más precisa del potencial de membrana se puede calcular utilizando la ecuación de GHK que con la ecuación de Millman.
Medición de potenciales en reposo
En algunas células, el potencial de membrana siempre está cambiando (como en las células marcapasos cardíacos). Para tales células nunca hay ningún "descanso" y el "potencial de reposo" Es un concepto teórico. Otras células con pocas funciones de transporte de membrana que cambian con el tiempo tienen un potencial de membrana en reposo que se puede medir insertando un electrodo en la célula. Los potenciales transmembrana también se pueden medir ópticamente con colorantes que cambian sus propiedades ópticas según el potencial de membrana.
Resumen de los valores de potencial en reposo en diferentes tipos de células
| Tipos de células | Potencial de reposo |
|---|---|
| Células musculares esqueléticas | -95 mV |
| Astroglia | -80 a -90 mV |
| Neuronas | -60 a -70 mV |
| Células musculares | -60 mV |
| Aorta tejido muscular musculoso | -45mV |
| Células de fotoreceptor | -40 mV |
| Celda de pelo (Cochlea) | -15 a -40mV |
| Erythrocytes | -8.4 mV |
| Condrocitos | -8mV |
Historia
Las corrientes de reposo en los nervios fueron medidas y descritas por Julius Bernstein en 1902, donde propuso una "Teoría de membrana" que explicaba el potencial de reposo del nervio y del músculo como potencial de difusión.

![E_{eq,K^+} = frac{RT}{zF} ln frac{[K^+]_{o}}{[K^+]_{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7eb1afcc5d7a5032ff24be5c403b43b1307b01e)
![E_{{eq,K^{+}}}=61.54mVlog {frac {[K^{+}]_{{o}}}{[K^{+}]_{{i}}}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d0b62ffda044574b1a52306113028c6a29c89f2)
![E_{{m}}={frac {RT}{F}}ln {left({frac {P_{{Na^{+}}}[Na^{+}]_{{o}}+P_{{K^{+}}}[K^{+}]_{{o}}+P_{{Cl^{-}}}[Cl^{-}]_{{i}}}{P_{{Na^{+}}}[Na^{+}]_{{i}}+P_{{K^{+}}}[K^{+}]_{{i}}+P_{{Cl^{-}}}[Cl^{-}]_{{o}}}}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef443116c02ee0a29c6f4d6f5a5fc571e530ec8)

