Politropo

En astrofísica, un politropo se refiere a una solución de la ecuación de Lane-Emden en la que la presión depende de la densidad en la forma

P=K*** *** ()n+1)/n,{displaystyle P=Krho ^{(n+1)/n}

donde P es presión, ρ es densidad y K es una constante de proporcionalidad. La constante n se conoce como índice politrópico; tenga en cuenta, sin embargo, que el índice politrópico tiene una definición alternativa con n como exponente.

Esta relación no necesita interpretarse como una ecuación de estado, que establece P como una función tanto de ρ como de T (la temperatura); sin embargo, en el caso particular descrito por la ecuación politrópica, existen otras relaciones adicionales entre estas tres cantidades, que juntas determinan la ecuación. Por lo tanto, esta es simplemente una relación que expresa una suposición sobre el cambio de presión con el radio en términos del cambio de densidad con el radio, dando una solución a la ecuación de Lane-Emden.

A veces, la palabra politropo puede referirse a una ecuación de estado que se parece a la relación termodinámica anterior, aunque esto es potencialmente confuso y debe evitarse. Es preferible referirse al fluido en sí mismo (a diferencia de la solución de la ecuación de Lane-Emden) como un fluido politrópico. La ecuación de estado de un fluido politrópico es lo suficientemente general como para que tales fluidos idealizados encuentren un amplio uso fuera del problema limitado de los politropos.

Se ha demostrado que el exponente politrópico (de un politropo) es equivalente a la derivada de presión del módulo volumétrico donde también se ha demostrado su relación con la ecuación de estado de Murnaghan. Por lo tanto, la relación politrópica es más adecuada para condiciones de presión relativamente baja (por debajo de 10⁷ Pa) y de alta presión (por encima de 10¹⁴ Pa) cuando la presión derivada del volumen módulo, que es equivalente al índice politropo, es casi constante.

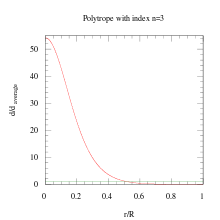
Modelos de ejemplo por índice politrópico

• Un índice n = 0 politropo se utiliza a menudo para modelar planetas rocosos. La razón es que n = 0 politropo tiene densidad constante, es decir, interior incompresible. Esta es una aproximación de orden cero para planetas rocosos (sólidos/líquidos).
• Las estrellas Neutron están bien modeladas por politropos con índice entre n = 0,5 y n = 1.
• Un politropo con índice n = 1,5 es un buen modelo para los núcleos estrella totalmente convectivos (como los de los gigantes rojos), enanos marrones, planetas gigantes gaseosos (como Júpiter). Con este índice, el exponente politrópico es 5/3, que es la relación de capacidad de calor (γ) para el gas monatámico. Para el interior de estrellas gaseosas (consistente con hidrógeno ionizado o helio), esto se deriva de una aproximación de gas ideal para las condiciones de convección natural.
• Un politropo con índice n = 1,5 es también un buen modelo para enanos blancos de baja masa, según la ecuación del estado de materia degenerada no relativista.
• Un politropo con índice n = 3 es un buen modelo para los núcleos de enanos blancos de masas superiores, según la ecuación del estado de materia degenerada relativista.
• Un politropo con índice n = 3 generalmente también se utiliza para modelar estrellas de la secuencia principal como el Sol, al menos en la zona de radiación, correspondiente al modelo estándar Eddington de la estructura estelar.
• Un politropo con índice n = 5 tiene un radio infinito. Corresponde al modelo plausible más simple de un sistema estelar autoconsistente, primero estudiado por Arthur Schuster en 1883, y tiene una solución exacta.
• Un politropo con índice n = corresponde a lo que se llama esfera estratémica, que es una esfera autogravitativa isotérmica de gas, cuya estructura es idéntica a la estructura de un sistema sin colisión de estrellas como un cluster globular. Esto se debe a que para un gas ideal, la temperatura es proporcional a ρ^1/n, tan infinito n corresponde a una temperatura constante.

In general as the polytropic index increases, the density distribution is more heavily weighted toward the center (or = 0) of the body.