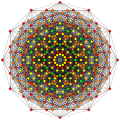
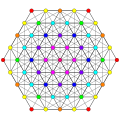
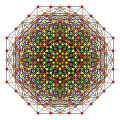
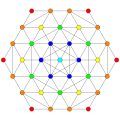
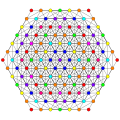
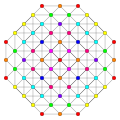
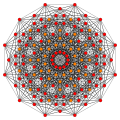
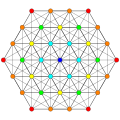
Politopo E7

Proyecciones ortoográficas en la E₇ Coxeter avión

321

231

132

En geometría heptadimensional, existen 127 politopos uniformes con simetría E₇. Las tres formas más simples son los politopos 321, 231 y 132, compuestos por 56, 126 y 576 vértices, respectivamente.Pueden visualizarse como proyecciones ortográficas simétricas en los planos de Coxeter del grupo de Coxeter E₇ y otros subgrupos.

Se pueden realizar proyecciones ortográficas simétricas de estos 127 politopos en los planos de Coxeter E₇, E₆, D₆, D₅, D₄, D₃, A₆, A₅, A₄, A₃ y A₂. A_k tiene simetría k+1, D_k tiene simetría 2(k-1), y E₆ y E₇ tienen simetría 12 y 18, respectivamente.

Para 10 de 127 politopos (7 anillos individuales y 3 truncamientos), se muestran en estos 9 planos de simetría, con vértices y aristas dibujados, y vértices coloreados según el número de vértices superpuestos en cada posición proyectiva.

#	Gráficos planos de Coxeter								Coxeter diagrama Símbolo Schläfli Nombres
	E7 [18]	E6	A6 [7x2]	A5 [6]	A4 D6 [10]	D5 [8]	A2 D4 [6]	A3 D3 [4]
1									231 (laq)
2									Rectificado 231 (rolaq)
3									Rectificado 132 (rolín)
4									132 (lin)
5									Birectified 321 (branq)
6									Rectificado 321 (ranq)
7									321 (naq)
8									truncado 231 (talq)
9									Truncated 132 (tilin)
10									Truncado 321 (tanq)

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Polytopes regulares, 3a edición, Dover Nueva York, 1973
• Kaleidoscopios: Escrituras seleccionadas de H.S.M. Coxeter, editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopios: Escrituras seleccionadas de H.S.M. Coxeter
  • H.S.M. Coxeter, Polytops regulares y semi regulares I[Mat. Zeit. 46 (1940) 380-407, MR 2,10]
  • H.S.M. Coxeter, Polytopes regulares y semi-regulares II[Math. Zeit. 188 (1985) 559-591]
  • H.S.M. Coxeter, Polytopes regulares y semi-regulares III[Mat. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The The The Theory of Uniform Polytopes and Honeycombs, Doctorado en Disertación, Universidad de Toronto, 1966
• Klitzing, Richard. "Politopes uniformes 7D (polyexa)".

v t e Convexos fundamentales politopes regulares y uniformes en dimensiones 2–10
Familia	An	Bn	I2p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Poligono regular	Triángulo	Plaza	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetraedro	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniforme polichoron	Pentachoron	16 celdas • Tesseract	Demitesseract	24 horas	120 celdas • 600 celdas
Uniforme 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniforme 6-polytope	6-simplex	6 orthoplex • 6-cubos	6-demicube	122 • 221
Uniforme 7-polytope	7-simplex	7-orthoplex • 7-cubo	7-demicube	132 • 231 • 321
Uniforme 8-polytope	8-simplex	8-orthoplex • 8-cubo	8-demicube	142 • 241 • 421
Uniforme 9-polytope	9-simplex	9 orthoplex • 9-cubo	9-demicube
Uniforme 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniforme uniforme n-polytope	n-simplex	n-ortoplex • n- ¡Cabrón!	n-Demicube	1k2 • 2k1 • k21	n- politopetopentagonal
Temas: Familias de politopo • Politopo regular • Lista de politopes y compuestos regulares