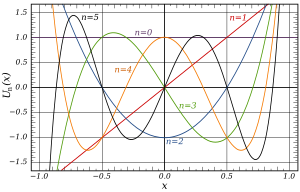
Polinomios de Chebyshev

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Secuencia polinómica

Parcela del polinomio Chebyshev del primer tipo T n(x) con n=5 en el plano complejo de -2-2i a 2+2i con colores creados con Mathematica 13.1 función ComplejoPlot3D

El Polinomios Chebyshev son dos secuencias de polinomios relacionados con las funciones cosina y sine, notados como $T_n(x)$ y $U_n(x)$ . Pueden definirse de varias maneras equivalentes, una de las cuales comienza con funciones trigonométricas:

El Polinomios Chebyshev de primer tipo $T_{n}$ se definen por

{displaystyle T_{n}(cos theta)=cos(ntheta).}

Del mismo modo, el Polinomios Chebyshev del segundo tipo $U_{n}$ se definen por

{displaystyle U_{n}(cos theta)sin theta =sin {big (}(n+1)theta {big)}.}

Que estas expresiones definen polinomios en $cos theta$ puede no ser obvio a primera vista, pero sigue por reescritura ${displaystyle cos(ntheta)}$ y ${displaystyle sin {big (}(n+1)theta {big)}}$ usando la fórmula de Moivre o usando las fórmulas de suma de ángulo para $cos$ y $sin$ repetidamente. Por ejemplo, las fórmulas de doble ángulo, que siguen directamente desde las fórmulas de suma de ángulo, pueden utilizarse para obtener ${displaystyle T_{2}(cos theta)=cos(2theta)=2cos ^{2}theta -1}$ y ${displaystyle U_{1}(cos theta)sin theta =sin(2theta)=2cos theta sin theta }$ , que son respectivamente un polinomio en $cos theta$ y un polinomio en $cos theta$ multiplicado por $sin theta$ . Por lo tanto ${displaystyle T_{2}(x)=2x^{2}-1}$ y ${displaystyle U_{1}(x)=2x}$ .

Una propiedad importante y conveniente de $T n (x)$ es que son ortogonales con respecto al producto interior:

{displaystyle langle f,grangle =int _{-1}^{1}f(x),g(x),{frac {mathrm {d} x}{sqrt {1-x^{2}}}},}

y $U n (x)$ son ortogonal con respecto a otro producto interno análogo, dado a continuación.

Los polinomios de Chebyshev $T n$ son polinomios con el mayor coeficiente principal posible cuyo valor absoluto en el intervalo $[-1, 1]$ está delimitado por 1. También son los "extremal" polinomios para muchas otras propiedades.

Los polinomios de Chebyshev son importantes en la teoría de la aproximación porque las raíces de $T n (x)$ , que también se denominan nodos de Chebyshev, se utilizan como puntos coincidentes para optimizar la interpolación de polinomios. El polinomio de interpolación resultante minimiza el problema del fenómeno de Runge y proporciona una aproximación cercana a la mejor aproximación polinomial a una función continua bajo la norma máxima, también llamada "minimax" criterio. Esta aproximación conduce directamente al método de cuadratura de Clenshaw-Curtis.

Estos polinomios recibieron su nombre de Pafnuty Chebyshev. La letra $T$ se usa debido a las transliteraciones alternativas del nombre Chebyshev como Tchebycheff, Tchebyshev (francés) o Tschebyschow (alemán).

Definiciones

Definición de recurrencia

Parcela de los primeros cinco

T n

Polinomios Chebyshev (primer tipo)

Los polinomios de Chebyshev de primera especie se obtienen a partir de la relación de recurrencia

{displaystyle {begin{aligned}T_{0}(x)&=1\T_{1}(x)&=x\T_{n+1}(x)&=2x,T_{n}(x)-T_{n-1}(x).end{aligned}}}

La recurrencia también permite representarlos explícitamente como el determinante de una matriz tridiagonal de tamaño $ktimes k$ :

{displaystyle T_{k}(x)=det {begin{bmatrix}x&1&0&dots &0\1&2x&1&dots &0\0&1&2x&ddots &vdots \vdots &vdots &ddots &ddots &1\0&0&dots &1&2xend{bmatrix}}}

La función generadora ordinaria para $T n$ es

{displaystyle sum _{n=0}^{infty }T_{n}(x),t^{n}={frac {1-tx}{1-2tx+t^{2}}}.}

Hay varias otras funciones generadoras para los polinomios de Chebyshev; la función generadora exponencial es

{displaystyle sum _{n=0}^{infty }T_{n}(x){frac {t^{n}}{n!}}={frac {1}{2}}!left(e^{tleft(x-{sqrt {x^{2}-1}}right)}+e^{tleft(x+{sqrt {x^{2}-1}}right)}right)=e^{tx}cosh left(t{sqrt {x^{2}-1}}right).}

La función generadora relevante para la teoría del potencial bidimensional y la expansión multipolar es

{displaystyle sum limits _{n=1}^{infty }T_{n}(x),{frac {t^{n}}{n}}=ln left({frac {1}{sqrt {1-2tx+t^{2}}}}right).}

Parcela de los primeros cinco

U n

Polinomios Chebyshev (segundo tipo)

Los polinomios de Chebyshev de segunda clase están definidos por la relación de recurrencia

{displaystyle {begin{aligned}U_{0}(x)&=1\U_{1}(x)&=2x\U_{n+1}(x)&=2x,U_{n}(x)-U_{n-1}(x).end{aligned}}}

Observe que los dos conjuntos de relaciones de recurrencia son idénticos, excepto para ${displaystyle T_{1}(x)=x}$ vs. ${displaystyle U_{1}(x)=2x}$ .La función generadora ordinaria para $U n$ es

{displaystyle sum _{n=0}^{infty }U_{n}(x),t^{n}={frac {1}{1-2tx+t^{2}}},}

y la función generadora exponencial es

{displaystyle sum _{n=0}^{infty }U_{n}(x){frac {t^{n}}{n!}}=e^{tx}!left(!cosh left(t{sqrt {x^{2}-1}}right)+{frac {x}{sqrt {x^{2}-1}}}sinh left(t{sqrt {x^{2}-1}}right)!right).}

Definición trigonométrica

Como se describe en la introducción, los polinomios de Chebyshev del primer tipo se pueden definir como polinomios únicos que satisfacen

{displaystyle T_{n}(x)={begin{cases}cos(narccos x)&{text{ if }}~|x|leq 1\cosh(noperatorname {arcosh} x)&{text{ if }}~xgeq 1\(-1)^{n}cosh(noperatorname {arcosh} (-x))&{text{ if }}~xleq -1end{cases}}}

o, en otras palabras, como los polinomios únicos que satisfacen

T_n(costheta)=cos(ntheta)

para $n = 0, 1, 2, 3, \dots$ que como punto técnico es una variante (transpuesta equivalente) de Schröder's ecuación. Es decir, $T n (x)$ es funcionalmente conjugado con $n x$ , codificado en la propiedad de anidamiento a continuación.

Los polinomios del segundo tipo satisfacen:

{displaystyle U_{n-1}(cos theta)sin theta =sin(ntheta),}

{displaystyle U_{n}(cos theta)={frac {sin {big (}(n+1),theta {big)}}{sin theta }},}

que es estructuralmente bastante similar al kernel de Dirichlet $D n (x)$ :

{displaystyle D_{n}(x)={frac {sin left((2n+1){dfrac {x}{2}},right)}{sin {dfrac {x}{2}}}}=U_{2n}!!left(cos {frac {x}{2}}right).}

(El kernel de Dirichlet, de hecho, coincide con lo que ahora se conoce como el polinomio de Chebyshev de cuarto tipo).

Ese $cos nx$ es un $n$ ésimo grado en $cos x$ se puede ver observando que $cos nx$ es la parte real de un lado de la fórmula de De Moivre. La parte real del otro lado es un polinomio en $cos x$ y $sin x$ , en el que todas las potencias de $sin x$ son pares y, por lo tanto, reemplazables a través de la identidad $cos 2 x + sin 2 x = 1$ . Por el mismo razonamiento, $sin nx$ es la parte imaginaria del polinomio, en el que todas las potencias de $sin x$ son impares y, por lo tanto, si se factoriza un factor de $sin x$ , los factores restantes se pueden reemplazar para crear un $(n -1)$ polinomio de primer grado en $cos x .$

La identidad es bastante útil junto con la fórmula generadora recursiva, ya que permite calcular el coseno de cualquier múltiplo entero de un ángulo únicamente en términos del coseno del ángulo base.

Los polinomios de Chebyshev del primer tipo se pueden calcular directamente a partir de la identidad de Euler

{displaystyle cos ktheta +isin ktheta =e^{iktheta }=(e^{itheta })^{k}=(cos theta +isin theta)^{k}.}

Expandiendo este último, se obtiene

{displaystyle (cos theta +isin theta)^{k}=sum limits _{j=0}^{k}{binom {k}{j}}i^{j}sin ^{j}theta cos ^{k-j}theta.}

Entonces, para conseguir la expresión para ${displaystyle cos ktheta }$ , uno debe mirar en la parte real de la expresión, que se obtiene de las sumas correspondientes a los índices. Observando ${displaystyle i^{2j}=(-1)^{j}}$ y ${displaystyle sin ^{2j}theta =(1-cos ^{2}theta)^{j}}$ , uno recibe la fórmula explícita

{displaystyle cos ktheta =sum limits _{j=0}^{lfloor k/2rfloor }{binom {k}{2j}}(cos ^{2}theta -1)^{j}cos ^{k-2j}theta}

lo que a su vez significa que

{displaystyle T_{k}(x)=sum limits _{j=0}^{lfloor k/2rfloor }{binom {k}{2j}}(x^{2}-1)^{j}x^{k-2j}.}

Alternativamente, los dos primeros polinomios de Chebyshev del primer tipo se calculan directamente a partir de la definición para ser

{displaystyle T_{0}(cos theta)=cos(0theta)=1}

{displaystyle T_{1}(cos theta)=cos theta}

mientras que el resto puede evaluarse utilizando una especialización de la identidad de producto a suma

{displaystyle 2cos ntheta cos theta =cos lbrack (n+1)theta rbrack +cos lbrack (n-1)theta rbrack }

como, por ejemplo,

{displaystyle {begin{aligned}T_{2}(cos theta)&=cos 2theta =2cos theta cos theta -1=2cos ^{2}theta -1.\T_{3}(cos theta)&=cos 3theta =2cos theta cos 2theta -cos theta =4cos ^{3}theta -3cos theta.end{aligned}}}

Por el contrario, una potencia entera arbitraria de funciones trigonométricas puede expresarse como una combinación lineal de funciones trigonométricas utilizando polinomios de Chebyshev.

{displaystyle cos ^{n}theta =2^{1-n}!mathop {mathop {{sum }'} _{j=0}^{n}} _{n-j,{text{even}}}!!{binom {n}{tfrac {n-j}{2}}},T_{j}(cos theta),}

donde el primer símbolo de la suma indica que la contribución $j = 0$ necesita ser reducido si aparece, y ${displaystyle T_{j}(cos theta)=cos(jtheta)}$ .

Un corolario inmediato es la expresión de exponenciación compleja en términos de polinomios de Chebyshev: dado $z = a + bi$ ,

{displaystyle {begin{aligned}z^{n}&=|z|^{n}!left(cos left(narccos {frac {a}{|z|}}right)+i{frac {b}{|b|}}sin left(narccos {frac {a}{|z|}}right)right)\&=|z|^{n},T_{n}!!!;left({frac {a}{|z|}}right)+ib|z|^{n-1} U_{n-1}!!!;left({frac {a}{|z|}}right).end{aligned}}}

Definición de polinomios conmutativos

Los polinomios de Chebyshev también se pueden caracterizar mediante el siguiente teorema:

Si ${displaystyle F_{n}(x)}$ es una familia de polinomios monicos con coeficientes en un campo de características ${displaystyle 0}$ tales que ${displaystyle deg F_{n}(x)=n}$ y ${displaystyle F_{m}(F_{n}(x))=F_{n}(F_{m}(x))}$ para todos $m$ y $n$ , entonces, hasta un simple cambio de variables, ya sea ${displaystyle F_{n}(x)=x^{n}}$ para todos $n$ o ${displaystyle F_{n}(x)=2*T_{n}(x/2)}$ para todos $n$ .

Definición de la ecuación de Pell

Los polinomios de Chebyshev también se pueden definir como las soluciones de la ecuación de Pell

{displaystyle T_{n}(x)^{2}-left(x^{2}-1right)U_{n-1}(x)^{2}=1}

en un anillo $R [x]$ . Por lo tanto, pueden generarse mediante la técnica estándar para las ecuaciones de Pell de tomar potencias de una solución fundamental:

{displaystyle T_{n}(x)+U_{n-1}(x),{sqrt {x^{2}-1}}=left(x+{sqrt {x^{2}-1}}right)^{n}~.}

Relaciones entre los dos tipos de polinomios de Chebyshev

Los polinomios de Chebyshev del primer y segundo tipo corresponden a un par complementario de secuencias de Lucas $Ṽ n (P, Q)$ y $\times n (P, Q)$ con parámetros $P = 2 x$ y $P = 1$ :

{displaystyle {begin{aligned}{tilde {U}}_{n}(2x,1)&=U_{n-1}(x),\{tilde {V}}_{n}(2x,1)&=2,T_{n}(x).end{aligned}}}

Se deduce que también satisfacen un par de ecuaciones de recurrencia mutua:

{displaystyle {begin{aligned}T_{n+1}(x)&=x,T_{n}(x)-(1-x^{2}),U_{n-1}(x),\U_{n+1}(x)&=x,U_{n}(x)+T_{n+1}(x).end{aligned}}}

El segundo de estos se puede reorganizar usando la definición de recurrencia para los polinomios de Chebyshev del segundo tipo para dar

{displaystyle T_{n}(x)={frac {1}{2}}{big (}U_{n}(x)-U_{n-2}(x){big)}.}

Usar esta fórmula iterativamente da la fórmula de suma

{displaystyle U_{n}(x)={begin{cases}2sum _{{text{ odd }}j}^{n}T_{j}(x)&{text{ for odd }}n.\2sum _{{text{ even }}j}^{n}T_{j}(x)-1&{text{ for even }}n,end{cases}}}

mientras se reemplaza $U_n(x)$ y ${displaystyle U_{n-2}(x)}$ usando la fórmula derivada para $T_n(x)$ da la relación de recurrencia para el derivado de $T_{n}$ :

{displaystyle 2,T_{n}(x)={frac {1}{n+1}},{frac {mathrm {d} }{mathrm {d} x}},T_{n+1}(x)-{frac {1}{n-1}},{frac {mathrm {d} }{mathrm {d} x}},T_{n-1}(x),qquad n=2,3,ldots }

Esta relación se utiliza en el método espectral de Chebyshev para resolver ecuaciones diferenciales.

Las desigualdades de Turán para los polinomios de Chebyshev son

0&&{text{ for }}-1<x0~.end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">Tn()x)2− − Tn− − 1()x)Tn+1()x)=1− − x2■0para− − 1.x.1yUn()x)2− − Un− − 1()x)Un+1()x)=1■0.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fn0} {fn0}fn1} {cH0} {cH0}n0}n1}n0}n0}n1n0}n0}n0}n0}n1n0}n0n1n1n1}n0}n1}n0n1}n1n0}n1n1n0}n1n1nKn1}n1}n1}n1}n1n1n0}nnnKnnKnKnKnKnKnKnKnKnKn1cH00n1cH0}n1}n1}n1n0&&{text{ for }}-1<x0~.end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d2594562076c60faa2f6b93a7247ea12aefe7e20" style="vertical-align: -2.671ex; width:71.654ex; height:6.509ex;"/>

Las relaciones integrales son

{displaystyle {begin{aligned}int _{-1}^{1}{frac {T_{n}(y)}{(y-x){sqrt {1-y^{2}}}}},mathrm {d} y&=pi ,U_{n-1}(x)~,\int _{-1}^{1}{frac {{sqrt {1-y^{2}}},U_{n-1}(y)}{y-x}},mathrm {d} y&=-pi ,T_{n}(x)end{aligned}}}

donde las integrales se consideran como valor principal.

Expresiones explícitas

Diferentes enfoques para definir los polinomios de Chebyshev conducen a diferentes expresiones explícitas como:

0\\&=nsum _{k=0}^{n}(-2)^{k}{frac {(n+k-1)!}{(n-k)!(2k)!}}(1-x)^{k}qquad qquad ~{text{ for }}~n>0\\&={}_{2}F_{1}!left(-n,n;{tfrac {1}{2}};{tfrac {1}{2}}(1-x)right)\end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">Tn()x)={}#⁡ ⁡ ()narccos⁡ ⁡ x)paraSilencioxSilencio≤ ≤ 112()()x− − x2− − 1)n+()x+x2− − 1)n)paraSilencioxSilencio≥ ≥ 1={}#⁡ ⁡ ()narccos⁡ ⁡ x)para− − 1≤ ≤ x≤ ≤ 1cosh⁡ ⁡ ()narcosh⁡ ⁡ x)para1≤ ≤ x()− − 1)ncosh⁡ ⁡ ()narcosh⁡ ⁡ ()− − x))parax≤ ≤ − − 1Tn()x)=.. k=0⌊n2⌋()n2k)()x2− − 1)kxn− − 2k=xn.. k=0⌊n2⌋()n2k)()1− − x− − 2)k=n2.. k=0⌊n2⌋()− − 1)k()n− − k− − 1)!k!()n− − 2k)!()2x)n− − 2kparan■0=n.. k=0n()− − 2)k()n+k− − 1)!()n− − k)!()2k)!()1− − x)kparan■0=2F1()− − n,n;12;12()1− − x)){displaystyle {begin{aligned}T_{n}(x) Condenado={begin{cases}cos(narccos x)qquad >{text{ for }~Principio}leq 1\\\\\{dfrac {1}{2} {bigg}{Big (}x-{sqrt {x^{2}-1}{} {f} {f} {f}} {f}}} {f}}}} {f}}}}} {f}}}} {f}}}}} {f}}}} { Grande. Grande. {x^{2}-1}{f} {f} {f}}} {f}}}} {f}}}} {f}} {f}}}}} {f}}}}}}}}}} {\f}}}}}} {\f}}}}}}} {\\f}}}}}}}}}}} {\\\\\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\}}}}}}}}}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} - 1\\end{cases}\\\\\\\\\T_{n}(x) ¿Por qué? ################################################################################################################################################################################################################################################################ {n}{2}sum} ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ ###{k=0}{n}(-2)}{k}{frac {(n+k-1)}{(n-k)!(2k)}}} {k}qquad qquad ~{text{ for for ¡No! {1}{2};{tfrac {1} {2} {1-x)right)\\end{aligned}}}}0\\&=nsum _{k=0}^{n}(-2)^{k}{frac {(n+k-1)!}{(n-k)!(2k)!}}(1-x)^{k}qquad qquad ~{text{ for }}~n>0\\&={}_{2}F_{1}!left(-n,n;{tfrac {1}{2}};{tfrac {1}{2}}(1-x)right)\end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7ed67409a66786efc49e5f154fadfbbaf57b6dd2" style="vertical-align: -39.505ex; width:72.772ex; height:80.176ex;"/>

con inversa

{displaystyle x^{n}=2^{1-n}mathop {{sum }'} _{j=0 atop j,equiv ,n{pmod {2}}}^{n}!!{binom {n}{tfrac {n-j}{2}}}!;T_{j}(x),}

donde el número primo en el símbolo de suma indica que la contribución de $j = 0$ debe reducirse a la mitad si aparece.

0\&=sum _{k=0}^{leftlfloor {frac {n}{2}}rightrfloor }(-1)^{k}{binom {n-k}{k}}~(2x)^{n-2k}&{text{ for }}~n>0\&=sum _{k=0}^{n}(-2)^{k}{frac {(n+k+1)!}{(n-k)!(2k+1)!}}(1-x)^{k}&{text{ for }}~n>0\&=(n+1) {}_{2}F_{1}left(-n,n+2;{tfrac {3}{2}};{tfrac {1}{2}}(1-x)right)\end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">Un()x)=()x+x2− − 1)n+1− − ()x− − x2− − 1)n+12x2− − 1=.. k=0⌊n2⌋()n+12k+1)()x2− − 1)kxn− − 2k=xn.. k=0⌊n2⌋()n+12k+1)()1− − x− − 2)k=.. k=0⌊n2⌋()2k− − ()n+1)k)()2x)n− − 2kparan■0=.. k=0⌊n2⌋()− − 1)k()n− − kk)()2x)n− − 2kparan■0=.. k=0n()− − 2)k()n+k+1)!()n− − k)!()2k+1)!()1− − x)kparan■0=()n+1)2F1()− − n,n+2;32;12()1− − x)){displaystyle {begin{aligned}U_{n}(x) sentimiento={frac {left(x+{sqrt {x^{2}-1}right)}{n+1}-left(x-{sqrt {x^{2}-1}right)}{n+1}{2{sqrt {x^{2}-1}}\\fn}\fnK}}\\fn}}\\fn}}\\\cH00}}\\\cH0}}}\\\cH0}}}\\\cH0}}}}}\\\ ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ ¿Qué? # {binom {2k-(n+1)}{k}~(2x)}{n-2k} {text{ fortext{ for }'n título0\=sum ¿Por qué? {n-k}{k}~(2x)}{n-2k} {fn} {fn} {fn} {fn} {fn} {fn} {fn+c+1)!}{(n-k+1)!}} {cn-x)} {cHFF} {fn} {fnfn0\\\\fn1}\\fn1}\\\\cH0cH0cH0cH00cH00cH00cH00cH00cH00cH00cH00cH00cH0cH00cH00cH00cH00cH00cH00}cH00cH00}cH00}cH00cH00cH00cH00cH00}cH00}cH00}cH00cH00}cH00cH00cH00}cH00cH {fnMicroc {3}}} {fnMicroc {2}}} {fnMicroc {1} {2}} {2}} {nMicroc}} {fnMicroc}}} {fnMicroc}}} {\fnMicroc}}}} {fnMicroc}}}}}\\\\\fn}}\\\\\fn\\\\\\\fnMicrob}}}}}}}}}}\\\\fn}}}}}}}}}}}}}}}\\\\\\\\fn}}}}}}}}\\\\\\\fn}}}}}}}}}}}\\\\\\\\\\\\fn0\&=sum _{k=0}^{leftlfloor {frac {n}{2}}rightrfloor }(-1)^{k}{binom {n-k}{k}}~(2x)^{n-2k}&{text{ for }}~n>0\&=sum _{k=0}^{n}(-2)^{k}{frac {(n+k+1)!}{(n-k)!(2k+1)!}}(1-x)^{k}&{text{ for }}~n>0\&=(n+1) {}_{2}F_{1}left(-n,n+2;{tfrac {3}{2}};{tfrac {1}{2}}(1-x)right)\end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/60b5f5ff4a60578a357624cc53f617a91321c8a5" style="vertical-align: -28.261ex; margin-bottom: -0.244ex; width:66.25ex; height:58.176ex;"/>

donde $2 F 1$ es una función hipergeométrica.

Propiedades

Simetría

{displaystyle {begin{aligned}T_{n}(-x)&=(-1)^{n},T_{n}(x)={begin{cases}T_{n}(x)quad &~{text{ for }}~n~{text{ even}}\\-T_{n}(x)quad &~{text{ for }}~n~{text{ odd}}end{cases}}\\\U_{n}(-x)&=(-1)^{n},U_{n}(x)={begin{cases}U_{n}(x)quad &~{text{ for }}~n~{text{ even}}\\-U_{n}(x)quad &~{text{ for }}~n~{text{ odd}}end{cases}}\end{aligned}}}

Es decir, los polinomios de Chebyshev de orden par tienen simetría par y, por lo tanto, solo contienen potencias pares de $x$ . Los polinomios de Chebyshev de orden impar tienen una simetría impar y, por lo tanto, solo contienen potencias impares de $x$ .

Raíces y extremos

Un polinomio de Chebyshev de cualquier tipo con grado $n$ tiene $n$ diferentes raíces simples, llamadas raíces de Chebyshev, en el intervalo $[-1, 1]$ . Las raíces del polinomio de Chebyshev del primer tipo a veces se denominan nodos de Chebyshev porque se usan como nodos en la interpolación de polinomios. Usando la definición trigonométrica y el hecho de que

{displaystyle cos left((2k+1){frac {pi }{2}}right)=0}

se puede mostrar que las raíces de $T n$ son

{displaystyle x_{k}=cos left({frac {pi (k+1/2)}{n}}right),quad k=0,ldotsn-1.}

Del mismo modo, las raíces de $U n$ son

x_{k}=cos left({frac {k}{n+1}}pi right),quad k=1,ldotsn.

Los extremos de $T n$ en el intervalo $- 1 \leq x \leq 1$ se encuentran en

{displaystyle x_{k}=cos left({frac {k}{n}}pi right),quad k=0,ldotsn.}

Una propiedad única de los polinomios de Chebyshev del primer tipo es que en el intervalo $-1 \leq x \leq 1$ todos los extremos tienen valores que son −1 o 1. Por lo tanto, estos polinomios tienen solo dos valores críticos finitos, la propiedad definitoria de los polinomios de Shabat. Tanto el primer como el segundo tipo de polinomio de Chebyshev tienen extremos en los extremos, dados por:

{displaystyle T_{n}(1)=1}

T_{n}(-1)=(-1)^{n}

{displaystyle U_{n}(1)=n+1}

{displaystyle U_{n}(-1)=(-1)^{n}(n+1).}

El extremo de $T_n(x)$ en el intervalo ${displaystyle -1leq xleq 1}$ Donde $0}" xmlns="http://www.w3.org/1998/Math/MathML">n■0{displaystyle n confiado0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27a6a5d982d54202a14f111cb8a49210501b2c96" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>$ se encuentran en $n+1$ valores de $x$ . Ellos son $pm 1$ , o ${displaystyle cos left({frac {2pi k}{d}}right)}$ Donde $2}" xmlns="http://www.w3.org/1998/Math/MathML">d■2{displaystyle d confiar2}2" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/239ca2d02537225ef87b98fa12958e8799bc697f" style="vertical-align: -0.338ex; width:5.477ex; height:2.176ex;"/>$ , ${displaystyle d;|;2n}$ , $<math alttext="{displaystyle 0<k0.k.d/2{displaystyle 0 0 se hizo 2 <img alt="{displaystyle 0<k$ y ${displaystyle (k,d)=1}$ , es decir, $k$ y $d$ son números relativamente primos.

Específicamente, cuando $n$ es incluso,

${displaystyle T_{n}(x)=1}$ si $x=pm 1$ , o $2}" xmlns="http://www.w3.org/1998/Math/MathML">d■2{displaystyle d confiar2}2" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/239ca2d02537225ef87b98fa12958e8799bc697f" style="vertical-align: -0.338ex; width:5.477ex; height:2.176ex;"/>$ y ${displaystyle 2n/d}$ es incluso. Hay ${displaystyle n/2+1}$ tales valores $x$ .
${displaystyle T_{n}(x)=-1}$ si $2}" xmlns="http://www.w3.org/1998/Math/MathML">d■2{displaystyle d confiar2}2" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/239ca2d02537225ef87b98fa12958e8799bc697f" style="vertical-align: -0.338ex; width:5.477ex; height:2.176ex;"/>$ y ${displaystyle 2n/d}$ Es extraño. Hay $n/2$ tales valores $x$ .

Cuando $n$ Es extraño.

${displaystyle T_{n}(x)=1}$ si $x=1$ , o $2}" xmlns="http://www.w3.org/1998/Math/MathML">d■2{displaystyle d confiar2}2" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/239ca2d02537225ef87b98fa12958e8799bc697f" style="vertical-align: -0.338ex; width:5.477ex; height:2.176ex;"/>$ y ${displaystyle 2n/d}$ es incluso. Hay $(n+1)/2$ tales valores $x$ .
${displaystyle T_{n}(x)=-1}$ si $x=-1$ , o $2}" xmlns="http://www.w3.org/1998/Math/MathML">d■2{displaystyle d confiar2}2" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/239ca2d02537225ef87b98fa12958e8799bc697f" style="vertical-align: -0.338ex; width:5.477ex; height:2.176ex;"/>$ y ${displaystyle 2n/d}$ Es extraño. Hay $(n+1)/2$ tales valores $x$ .

Este resultado se ha generalizado en soluciones ${displaystyle U_{n}(x)pm 1=0}$ , y a ${displaystyle V_{n}(x)pm 1=0}$ y ${displaystyle W_{n}(x)pm 1=0}$ para polinomios Chebyshev de la tercera y cuarta clase, respectivamente.

Diferenciación e integración

Las derivadas de los polinomios pueden ser menos que sencillas. Derivando los polinomios en sus formas trigonométricas, se puede demostrar que:

{displaystyle {begin{aligned}{frac {mathrm {d} T_{n}}{mathrm {d} x}}&=nU_{n-1}\{frac {mathrm {d} U_{n}}{mathrm {d} x}}&={frac {(n+1)T_{n+1}-xU_{n}}{x^{2}-1}}\{frac {mathrm {d} ^{2}T_{n}}{mathrm {d} x^{2}}}&=n,{frac {nT_{n}-xU_{n-1}}{x^{2}-1}}=n,{frac {(n+1)T_{n}-U_{n}}{x^{2}-1}}.end{aligned}}}

Las últimas dos fórmulas pueden ser numéricamente problemáticas debido a la división por cero (0/0 forma indeterminada, específicamente) en $x = 1$ y $x = -1$ . Se puede demostrar que:

{displaystyle {begin{aligned}left.{frac {mathrm {d} ^{2}T_{n}}{mathrm {d} x^{2}}}right|_{x=1}!!&={frac {n^{4}-n^{2}}{3}},\left.{frac {mathrm {d} ^{2}T_{n}}{mathrm {d} x^{2}}}right|_{x=-1}!!&=(-1)^{n}{frac {n^{4}-n^{2}}{3}}.end{aligned}}}

Prueba

El segundo derivado del polinomio Chebyshev del primer tipo es

{displaystyle T''_{n}=n,{frac {nT_{n}-xU_{n-1}}{x^{2}-1}}}

que, si se evalúa como se muestra anteriormente, plantea un problema porque es indeterminado $x = \pm1$ . Puesto que la función es un polinomio, (todos) los derivados deben existir para todos los números reales, por lo que el tomar para limitar la expresión anterior debe producir los valores deseados – tomando el límite como $x \to 1$ :

{displaystyle T''_{n}(1)=lim _{xto 1}n,{frac {nT_{n}-xU_{n-1}}{x^{2}-1}}}

Factorización del denominador:

{displaystyle T''_{n}(1)=lim _{xto 1}n,{frac {nT_{n}-xU_{n-1}}{(x+1)(x-1)}}=lim _{xto 1}n,{frac {dfrac {nT_{n}-xU_{n-1}}{x-1}}{x+1}}.}

Puesto que el límite en su conjunto debe existir, el límite del numerador y el denominador debe existir independientemente, y

{displaystyle T''_{n}(1)=n,{frac {displaystyle {lim _{xto 1}},{frac {nT_{n}-xU_{n-1}}{x-1}}}{displaystyle {lim _{xto 1}},(x+1)}}={frac {n}{2}}lim _{xto 1}{frac {nT_{n}-xU_{n-1}}{x-1}}.}

El denominador (todavía) limita a cero, lo que implica que el numerador debe limitarse a cero, es decir. $U n - 1 1) nT n 1) n$ que será útil más adelante. Dado que el numerador y el denominador se limitan a cero, la regla de L'Hôpital se aplica:

{displaystyle {begin{aligned}T''_{n}(1)&={frac {n}{2}},lim _{xto 1},{frac {{frac {mathrm {d} }{mathrm {d} x}}left(n,T_{n}-x,U_{n-1}right),}{,{frac {mathrm {d} }{mathrm {d} x}}(x-1)}}\&={frac {n}{2}}lim _{xto 1}{frac {mathrm {d} }{mathrm {d} x}}left(n,T_{n}-x,U_{n-1}right)\&={frac {n}{2}}lim _{xto 1}left(;n^{2},U_{n-1}-U_{n-1}-x{frac {mathrm {d} }{mathrm {d} x}}left(U_{n-1}right);right)\&={frac {n}{2}}left(,n^{2},U_{n-1}(1)-U_{n-1}(1)-lim _{xto 1}x,{frac {mathrm {d} }{mathrm {d} x}}left(U_{n-1}right),right)\&={frac {n^{4}}{2}}-{frac {n^{2}}{2}}-{frac {1}{2}}lim _{xto 1}{frac {mathrm {d} }{mathrm {d} x}}left(n,U_{n-1}right)\&={frac {n^{4}}{2}}-{frac {n^{2}}{2}}-{frac {T''_{n}(1)}{2}}\T''_{n}(1)&={frac {n^{4}-n^{2}}{3}}.\end{aligned}}}

La prueba $x = 1 -$ es similar, con el hecho de que $T n (1) - (-1) n$ ser importante.

La fórmula más general establece:

{displaystyle left.{frac {d^{p}T_{n}}{dx^{p}}}right|_{x=pm 1}!!=(pm 1)^{n+p}prod _{k=0}^{p-1}{frac {n^{2}-k^{2}}{2k+1}}~,}

que es de gran utilidad en la solución numérica de problemas de valores propios.

Además, tenemos

{displaystyle {frac {mathrm {d} ^{p}}{mathrm {d} x^{p}}},T_{n}(x)=2^{p},nmathop {{sum }'} _{0leq kleq n-p atop k,equiv ,n-p{pmod {2}}}{binom {{frac {n+p-k}{2}}-1}{frac {n-p-k}{2}}}{frac {left({frac {n+p+k}{2}}-1right)!}{left({frac {n-p+k}{2}}right)!}},T_{k}(x),~qquad pgeq 1,}

donde el primo en los símbolos de suma significa que el término aportado por $k = 0$ debe dividirse por la mitad, si aparece.

Con respecto a la integración, la primera derivada de $T n$ implica que

{displaystyle int U_{n},mathrm {d} x={frac {T_{n+1}}{n+1}}}

y la relación de recurrencia para los polinomios de primer tipo que involucran derivadas establece que para $n \geq 2$

{displaystyle int T_{n},mathrm {d} x={frac {1}{2}},left({frac {T_{n+1}}{n+1}}-{frac {T_{n-1}}{n-1}}right)={frac {n,T_{n+1}}{n^{2}-1}}-{frac {x,T_{n}}{n-1}}.}

La última fórmula se puede manipular aún más para expresar la integral de $T n$ como una función de polinomios de Chebyshev del primer tipo solamente:

{displaystyle {begin{aligned}int T_{n},mathrm {d} x&={frac {n}{n^{2}-1}}T_{n+1}-{frac {1}{n-1}}T_{1}T_{n}\&={frac {n}{n^{2}-1}},T_{n+1}-{frac {1}{2(n-1)}},(T_{n+1}+T_{n-1})\&={frac {1}{2(n+1)}},T_{n+1}-{frac {1}{2(n-1)}},T_{n-1}.end{aligned}}}

Además, tenemos

{displaystyle int _{-1}^{1}T_{n}(x),mathrm {d} x={begin{cases}{frac {(-1)^{n}+1}{1-n^{2}}}&{text{ if }}~nneq 1\0&{text{ if }}~n=1.end{cases}}}

Productos de polinomios de Chebyshev

Los polinomios de Chebyshev del primer tipo satisfacen la relación

{displaystyle T_{m}(x),T_{n}(x)={tfrac {1}{2}}!left(T_{m+n}(x)+T_{|m-n|}(x)right)!,qquad forall m,ngeq 0,}

que se demuestra fácilmente a partir de la fórmula de producto a suma para el coseno,

{displaystyle 2cos alpha ,cos beta =cos(alpha +beta)+cos(alpha -beta).}

Para $n = 1$ esto da como resultado la fórmula de recurrencia ya conocida, simplemente dispuesta de manera diferente y con $n = 2$ forma la relación de recurrencia para todos los polinomios de Chebyshev indexados pares o impares (dependiendo de la paridad del $m$ ) lo que implica la igualdad o imparidad de estos polinomios. A partir de esta expansión del producto se pueden concluir tres fórmulas más útiles para evaluar los polinomios de Chebyshev:

{displaystyle {begin{aligned}T_{2n}(x)&=2,T_{n}^{2}(x)-T_{0}(x)&&=2T_{n}^{2}(x)-1,\T_{2n+1}(x)&=2,T_{n+1}(x),T_{n}(x)-T_{1}(x)&&=2,T_{n+1}(x),T_{n}(x)-x,\T_{2n-1}(x)&=2,T_{n-1}(x),T_{n}(x)-T_{1}(x)&&=2,T_{n-1}(x),T_{n}(x)-x.end{aligned}}}

Los polinomios del segundo tipo satisfacen la relación similar

{displaystyle T_{m}(x),U_{n}(x)={begin{cases}{frac {1}{2}}left(U_{m+n}(x)+U_{n-m}(x)right),&~{text{ if }}~ngeq m-1,\\{frac {1}{2}}left(U_{m+n}(x)-U_{m-n-2}(x)right),&~{text{ if }}~nleq m-2.end{cases}}}

(con la definición $U -1 \equiv 0$ por convención). también satisfacen

{displaystyle U_{m}(x),U_{n}(x)=sum _{k=0}^{n},U_{m-n+2k}(x)=sum _{underset {text{ step 2 }}{p=m-n}}^{m+n}U_{p}(x)~.}

para $m \geq n$ . Para $n = 2$ esta recurrencia se reduce a

{displaystyle U_{m+2}(x)=U_{2}(x),U_{m}(x)-U_{m}(x)-U_{m-2}(x)=U_{m}(x),{big (}U_{2}(x)-1{big)}-U_{m-2}(x)~,}

que establece la paridad o imparidad de los polinomios de Chebyshev indexados pares o impares de segunda especie dependiendo de si $m$ empieza por 2 o 3.

Propiedades de composición y divisibilidad

Las definiciones trigonométricas de $T n$ y $U n$ implica la composición o las propiedades de anidamiento

{displaystyle {begin{aligned}T_{mn}(x)&=T_{m}(T_{n}(x)),\U_{mn-1}(x)&=U_{m-1}(T_{n}(x))U_{n-1}(x).end{aligned}}}

Para $T mn$ el orden de composición puede invertirse, haciendo que la familia de funciones polinómicas $T n$ un semigrupo conmutativo bajo composición.

Dado que $T m (x)$ es divisible por $x$ si $m$ es impar, se sigue que $T mn (x)$ es divisible por $T n (x)$ si $m$ es impar. Además, $U mn -1 (x)$ es divisible por $U n -1 (x)$ , y en el caso de que $m$ sea par, divisible por $T n (x) U n -1 (x)$ .

Ortogonalidad

Tanto $T n$ como $U n$ forman una secuencia de polinomios ortogonales. Los polinomios del primer tipo $T n$ son ortogonales con respecto al peso

{displaystyle {frac {1}{sqrt {1-x^{2}}}},}

en el intervalo $[-1, 1]$ , es decir, tenemos:

{displaystyle int _{-1}^{1}T_{n}(x),T_{m}(x),{frac {mathrm {d} x}{sqrt {1-x^{2}}}}={begin{cases}0&~{text{ if }}~nneq m,\\pi &~{text{ if }}~n=m=0,\\{frac {pi }{2}}&~{text{ if }}~n=mneq 0.end{cases}}}

Esto se puede probar haciendo $x = cos θ$ y usando la identidad definitoria $T n (cos θ) = cos(nθ).$

De manera similar, los polinomios del segundo tipo $U n$ son ortogonales con respecto al peso

{displaystyle {sqrt {1-x^{2}}}}

en el intervalo $[-1, 1]$ , es decir, tenemos:

{displaystyle int _{-1}^{1}U_{n}(x),U_{m}(x),{sqrt {1-x^{2}}},mathrm {d} x={begin{cases}0&~{text{ if }}~nneq m,\{frac {pi }{2}}&~{text{ if }}~n=m.end{cases}}}

(La medida $\sqrt 1 - x 2 d x$ es, dentro de una constante de normalización, la distribución semicircular de Wigner).

Estas propiedades de ortogonalidad se derivan del hecho de que los polinomios de Chebyshev resuelven las ecuaciones diferenciales de Chebyshev

{displaystyle (1-x^{2})y''-xy'+n^{2}y=0,}

{displaystyle (1-x^{2})y''-3xy'+n(n+2)y=0,}

que son ecuaciones diferenciales de Sturm-Liouville. Es una característica general de tales ecuaciones diferenciales que existe un conjunto distinguido de soluciones ortonormales. (Otra forma de definir los polinomios de Chebyshev es como las soluciones de esas ecuaciones).

El $T n$ también satisface una condición de ortogonalidad discreta:

{displaystyle sum _{k=0}^{N-1}{T_{i}(x_{k}),T_{j}(x_{k})}={begin{cases}0&~{text{ if }}~ineq j,\N&~{text{ if }}~i=j=0,\{frac {N}{2}}&~{text{ if }}~i=jneq 0,end{cases}}}

donde $N$ es cualquier número entero mayor que $max(i, j)$ , y $x k$ son los $N$ nodos de Chebyshev (ver arriba) de $T N (x)$ :

{displaystyle x_{k}=cos left(pi ,{frac {2k+1}{2N}}right)quad ~{text{ for }}~k=0,1,dotsN-1.}

Para los polinomios de segunda clase y cualquier número entero $N > i + j$ con los mismos nodos de Chebyshev $x k$ , hay sumas similares:

{displaystyle sum _{k=0}^{N-1}{U_{i}(x_{k}),U_{j}(x_{k})left(1-x_{k}^{2}right)}={begin{cases}0&{text{ if }}~ineq j,\{frac {N}{2}}&{text{ if }}~i=j,end{cases}}}

y sin la función de peso:

{displaystyle sum _{k=0}^{N-1}{U_{i}(x_{k}),U_{j}(x_{k})}={begin{cases}0&~{text{ if }}~inot equiv j{pmod {2}},\Ncdot (1+min{i,j})&~{text{ if }}~iequiv j{pmod {2}}.end{cases}}}

Para cualquier número entero $N > i + j$ , basado en los $N$ ceros de $U N (x)$ :

{displaystyle y_{k}=cos left(pi ,{frac {k+1}{N+1}}right)quad ~{text{ for }}~k=0,1,dotsN-1,}

uno puede obtener la suma:

{displaystyle sum _{k=0}^{N-1}{U_{i}(y_{k}),U_{j}(y_{k})(1-y_{k}^{2})}={begin{cases}0&~{text{ if }}ineq j,\{frac {N+1}{2}}&~{text{ if }}i=j,end{cases}}}

y de nuevo sin la función de peso:

{displaystyle sum _{k=0}^{N-1}{U_{i}(y_{k}),U_{j}(y_{k})}={begin{cases}0&~{text{ if }}~inot equiv j{pmod {2}},\{bigl (}min{i,j}+1{bigr)}{bigl (}N-max{i,j}{bigr)}&~{text{ if }}~iequiv j{pmod {2}}.end{cases}}}

Norma ∞ mínima

Para cualquier $n \geq 1$ , entre los polinomios de grado $n$ con coeficiente principal 1 (polinomios mónicos),

{displaystyle f(x)={frac {1}{,2^{n-1},}},T_{n}(x)}

es aquel cuyo valor absoluto máximo en el intervalo [−1, 1] es mínimo.

Este valor absoluto máximo es

{frac {1}{2^{n-1}}}

y $| f (x) |$ alcanza este máximo exactamente $n + 1$ veces en

{displaystyle x=cos {frac {kpi }{n}}quad {text{for }}0leq kleq n.}

Prueba

Supongamos que $w n () x)$ es un polinomio de grado $n$ con coeficiente líder 1 con valor absoluto máximo en el intervalo $[1, a 1]$ menos que $1 / 2 n - 1$ .

Define

{displaystyle f_{n}(x)={frac {1}{,2^{n-1},}},T_{n}(x)-w_{n}(x)}

Porque en puntos extremos $T n$ tenemos

<math alttext="{displaystyle {begin{aligned}|w_{n}(x)|&0qquad {text{ for }}~x=cos {frac {2kpi }{n}}~&&{text{ where }}0leq 2kleq n\f_{n}(x)&Silenciown()x)Silencio.Silencio12n− − 1Tn()x)Silenciofn()x)■0parax=#⁡ ⁡ 2kπ π nDonde0≤ ≤ 2k≤ ≤ nfn()x).0parax=#⁡ ⁡ ()2k+1)π π nDonde0≤ ≤ 2k+1≤ ≤ n{displaystyle {begin{aligned}Princew_{n}(x) tocando {1}{2^{n-1}}T_{n}(x)right remain\f_{n}(x) ################################################################################################################################################################################################################################################################<img alt="{displaystyle {begin{aligned}|w_{n}(x)|&0qquad {text{ for }}~x=cos {frac {2kpi }{n}}~&&{text{ where }}0leq 2kleq n\f_{n}(x)&

Del teorema de valor intermedio, $f n () x)$ al menos $n$ raíces. Sin embargo, esto es imposible, como $f n () x)$ es un polinomio de grado $n - 1$ , por lo que el teorema fundamental del álgebra implica que tiene a la mayoría $n - 1$ raíces.

Observación

Por el teorema de la equioscilación, entre todos los polinomios de grado $\leq n$ , el polinomio $f$ minimiza $‖ f ‖ \infty$ en $[-1, 1]$ si y solo si hay $n + 2$ puntos $-1 \leq x 0 < x 1 < \dots < x n + 1 \leq 1$ tal que $| f (x i) | = ‖ f ‖ \infty .$

Por supuesto, el polinomio nulo en el intervalo $[-1, 1]$ se puede aproximar por sí mismo y minimiza el $\infty$ -norma.

Arriba, sin embargo, $| f |$ alcanza su máximo solo $n + 1$ veces porque estamos buscando el mejor polinomio de grado $n \geq 1$ (por lo que no se puede utilizar el teorema evocado anteriormente).

Polinomios de Chebyshev como casos especiales de familias de polinomios más generales

Los polinomios Chebyshev son un caso especial de los polinomios ultrasféricos o Gegenbauer ${displaystyle C_{n}^{(lambda)}(x)}$ , que ellos mismos son un caso especial de los polinomios Jacobi ${displaystyle P_{n}^{(alphabeta)}(x)}$ :

{displaystyle {begin{aligned}T_{n}(x)&={frac {n}{2}}lim _{qto 0}{frac {1}{q}},C_{n}^{(q)}(x)qquad ~{text{ if }}~ngeq 1,\&={frac {1}{binom {n-{frac {1}{2}}}{n}}}P_{n}^{left(-{frac {1}{2}},-{frac {1}{2}}right)}(x)={frac {2^{2n}}{binom {2n}{n}}}P_{n}^{left(-{frac {1}{2}},-{frac {1}{2}}right)}(x)~,\U_{n}(x)&=C_{n}^{(1)}(x)\&={frac {n+1}{binom {n+{frac {1}{2}}}{n}}}P_{n}^{left({frac {1}{2}},{frac {1}{2}}right)}(x)={frac {2^{2n+1}}{binom {2n+2}{n+1}}}P_{n}^{left({frac {1}{2}},{frac {1}{2}}right)}(x)~.end{aligned}}}

Los polinomios de Chebyshev también son un caso especial de los polinomios de Dickson:

{displaystyle D_{n}(2xalphaalpha ^{2})=2alpha ^{n}T_{n}(x),}

{displaystyle E_{n}(2xalphaalpha ^{2})=alpha ^{n}U_{n}(x).,}

En particular, cuando ${displaystyle alpha ={tfrac {1}{2}}}$ , están relacionados por ${displaystyle D_{n}(x,{tfrac {1}{4}})=2^{1-n}T_{n}(x)}$ y ${displaystyle E_{n}(x,{tfrac {1}{4}})=2^{-n}U_{n}(x)}$ .

Otras propiedades

Las curvas dadas por $y = T n (x)$ , o de manera equivalente, por las ecuaciones paramétricas $y = T n (cos θ) = cos nθ$ , $x = cos θ$ , son un caso especial de curvas de Lissajous con relación de frecuencia igual a $n.$

Similar a la fórmula

{displaystyle T_{n}(cos theta)=cos(ntheta),}

tenemos la fórmula análoga

{displaystyle T_{2n+1}(sin theta)=(-1)^{n}sin left(left(2n+1right)theta right).}

Para $x \neq 0$ ,

{displaystyle T_{n}!left({frac {x+x^{-1}}{2}}right)={frac {x^{n}+x^{-n}}{2}}}

{displaystyle x^{n}=T_{n}!left({frac {x+x^{-1}}{2}}right)+{frac {x-x^{-1}}{2}} U_{n-1}!left({frac {x+x^{-1}}{2}}right),}

que se deriva del hecho de que esto se cumple por definición para $x = e iθ$ .

Ejemplos

Primer tipo

Los primeros pocos polinomios Chebyshev del primer tipo en el dominio

-1 - x 1

: El apartamento

T 0

T 1

T 2

T 3

T 4

T 5

Los primeros polinomios de Chebyshev del primer tipo son OEIS: A028297

{displaystyle {begin{aligned}T_{0}(x)&=1\T_{1}(x)&=x\T_{2}(x)&=2x^{2}-1\T_{3}(x)&=4x^{3}-3x\T_{4}(x)&=8x^{4}-8x^{2}+1\T_{5}(x)&=16x^{5}-20x^{3}+5x\T_{6}(x)&=32x^{6}-48x^{4}+18x^{2}-1\T_{7}(x)&=64x^{7}-112x^{5}+56x^{3}-7x\T_{8}(x)&=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1\T_{9}(x)&=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x\T_{10}(x)&=512x^{10}-1280x^{8}+1120x^{6}-400x^{4}+50x^{2}-1\T_{11}(x)&=1024x^{11}-2816x^{9}+2816x^{7}-1232x^{5}+220x^{3}-11xend{aligned}}}

Segundo tipo

Los primeros pocos polinomios Chebyshev del segundo tipo en el dominio

-1 - x 1

: El apartamento

U 0

U 1

U 2

U 3

U 4

U 5

. Aunque no visible en la imagen,

U n 1) n + 1

U n ()-1) n + 1)(-1) n

Los primeros polinomios de Chebyshev del segundo tipo son OEIS: A053117

{displaystyle {begin{aligned}U_{0}(x)&=1\U_{1}(x)&=2x\U_{2}(x)&=4x^{2}-1\U_{3}(x)&=8x^{3}-4x\U_{4}(x)&=16x^{4}-12x^{2}+1\U_{5}(x)&=32x^{5}-32x^{3}+6x\U_{6}(x)&=64x^{6}-80x^{4}+24x^{2}-1\U_{7}(x)&=128x^{7}-192x^{5}+80x^{3}-8x\U_{8}(x)&=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1\U_{9}(x)&=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10xend{aligned}}}

Como conjunto base

La función no monetaria (top)

Sí. = x 3 H () - x)

, donde

H

es la función Heaviside step, y (abajo) la quinta suma parcial de su expansión Chebyshev. La séptima suma es indistinguible de la función original en la resolución del gráfico.

En el espacio de Sobolev apropiado, el conjunto de polinomios de Chebyshev forman una base ortonormal, de modo que una función en el mismo espacio puede, en $-1 \leq x \leq 1$ , se expresará a través de la expansión:

f(x)=sum _{n=0}^{infty }a_{n}T_{n}(x).

Además, como se mencionó anteriormente, los polinomios de Chebyshev forman una base ortogonal que (entre otras cosas) implica que los coeficientes $a n$ se puede determinar fácilmente mediante la aplicación de un producto interno. Esta suma se denomina serie de Chebyshev o expansión de Chebyshev.

Dado que una serie de Chebyshev está relacionada con una serie de coseno de Fourier a través de un cambio de variables, todos los teoremas, identidades, etc. que se aplican a las series de Fourier tienen una contrapartida de Chebyshev. Estos atributos incluyen:

Los polinomios Chebyshev forman un sistema ortogonal completo.
La serie Chebyshev converge a $f () x)$ si la función es lisa y continua. El requisito de suavidad puede ser relajado en la mayoría de los casos - siempre y cuando haya un número finito de discontinuidades en $f () x)$ y sus derivados.
En una discontinuidad, la serie convergerá al promedio de los límites derecho e izquierdo.

La abundancia de teoremas e identidades heredados de las series de Fourier hacen que los polinomios de Chebyshev sean herramientas importantes en el análisis numérico; por ejemplo, son las funciones de base de propósito general más populares utilizadas en el método espectral, a menudo a favor de las series trigonométricas debido a la convergencia generalmente más rápida para las funciones continuas (el fenómeno de Gibbs sigue siendo un problema).

Ejemplo 1

Considere la expansión de Chebyshev de $log(1 + x)$ . Uno puede expresar

{displaystyle log(1+x)=sum _{n=0}^{infty }a_{n}T_{n}(x)~.}

Se pueden encontrar los coeficientes $a n$ mediante la aplicación de un producto interno o mediante la condición de ortogonalidad discreta. Para el producto interior,

{displaystyle int _{-1}^{+1},{frac {T_{m}(x),log(1+x)}{sqrt {1-x^{2}}}},mathrm {d} x=sum _{n=0}^{infty }a_{n}int _{-1}^{+1}{frac {T_{m}(x),T_{n}(x)}{sqrt {1-x^{2}}}},mathrm {d} x,}

que da

0.end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">an={}− − log⁡ ⁡ 2paran=0,− − 2()− − 1)nnparan■0.{displaystyle a_{n}={begin{cases}-log 2 {fn} {fn} {fn} {fn} {fnfnfnfn} {fnfnfn} {fnfnfnfnfnfnfnfnfnfnfnfnfnMicrosoft Sans Serif}0.end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f8716fedc562f9397a8b67bcf27f2fcf6dbc8804" style="vertical-align: -3.171ex; width:28.606ex; height:7.509ex;"/>

Alternativamente, cuando no se puede evaluar el producto interno de la función que se está aproximando, la condición de ortogonalidad discreta proporciona un resultado a menudo útil para los coeficientes aproximados,

{displaystyle a_{n}approx {frac {,2-delta _{0n},}{N}},sum _{k=0}^{N-1}T_{n}(x_{k}),log(1+x_{k}),}

donde $δ ij$ es la función delta de Kronecker y $x k$ son las $N$ Ceros de Gauss-Chebyshev de $T N (x)$ :

{displaystyle x_{k}=cos left({frac {pi left(k+{tfrac {1}{2}}right)}{N}}right).}

Para cualquier $N$ , estos coeficientes aproximados proporcionan una aproximación exacta a la función en $x k$ con un error controlado entre esos puntos. Los coeficientes exactos se obtienen con $N = \infty$ , representando así la función exactamente en todos los puntos en $[-1, 1]$ . La tasa de convergencia depende de la función y su suavidad.

Esto nos permite calcular los coeficientes aproximados $a n$ de manera muy eficiente a través de la transformada de coseno discreta

{displaystyle a_{n}approx {frac {2-delta _{0n}}{N}}sum _{k=0}^{N-1}cos left({frac {npi left(,k+{tfrac {1}{2}}right)}{N}}right)log(1+x_{k}).}

Ejemplo 2

Para dar otro ejemplo:

{displaystyle {begin{aligned}(1-x^{2})^{alpha }&=-{frac {1}{sqrt {pi }}},{frac {Gamma left({tfrac {1}{2}}+alpha right)}{Gamma (alpha +1)}}+2^{1-2alpha },sum _{n=0}(-1)^{n},{2alpha choose alpha -n},T_{2n}(x)\&=2^{-2alpha },sum _{n=0}(-1)^{n},{2alpha +1 choose alpha -n},U_{2n}(x).end{aligned}}}

Sumas parciales

Las sumas parciales de

f(x)=sum _{n=0}^{infty }a_{n}T_{n}(x)

son muy útiles en la aproximación de diversas funciones y en la solución de ecuaciones diferenciales (ver método espectral). Dos métodos comunes para determinar los coeficientes $a n$ son mediante el uso del producto interno como en Galerkin& #39;sy mediante el uso de la colocación que está relacionada con la interpolación.

Como interpolante, los coeficientes $N$ de los $(N - 1)$ La primera suma parcial generalmente se obtiene en los puntos de Chebyshev-Gauss-Lobatto (o cuadrícula de Lobatto), lo que da como resultado un error mínimo y evita el fenómeno de Runge asociado con una cuadrícula uniforme. Esta colección de puntos corresponde a los extremos del polinomio de mayor orden en la suma, más los puntos extremos y viene dada por:

{displaystyle x_{k}=-cos left({frac {kpi }{N-1}}right);qquad k=0,1,dotsN-1.}

Polinomio en forma de Chebyshev

Un polinomio arbitrario de grado $N$ se puede escribir en términos de los polinomios de Chebyshev del primer tipo. Tal polinomio $p (x)$ es de la forma

{displaystyle p(x)=sum _{n=0}^{N}a_{n}T_{n}(x).}

Los polinomios en forma de Chebyshev se pueden evaluar mediante el algoritmo de Clenshaw.

Familias de polinomios relacionados con los polinomios de Chebyshev

Polynomials denoted ${displaystyle C_{n}(x)}$ y ${displaystyle S_{n}(x)}$ estrechamente relacionado con los polinomios Chebyshev se utilizan a veces. Se definen por

{displaystyle C_{n}(x)=2T_{n}left({frac {x}{2}}right),qquad S_{n}(x)=U_{n}left({frac {x}{2}}right)}

y satisfacer

{displaystyle C_{n}(x)=S_{n}(x)-S_{n-2}(x).}

A. F. Horadam llamó a los polinomios ${displaystyle C_{n}(x)}$ Polinomios de Vieta-Lucas y los denotó ${displaystyle v_{n}(x)}$ . Llamó a los polinomios ${displaystyle S_{n}(x)}$ polinomios de Vieta-Fibonacci y los denotó ${displaystyle V_{n}(x)}$ . Las listas de ambos conjuntos de polinomios se dan en Viète Opera Mathematica, Capítulo IX, Teoremas VI y VII. Los polinomios de Vieta-Lucas y Vieta-Fibonacci son, hasta el poder de un argumento real $i$ y un cambio de índice en el caso de este último, igual a los polinomios Lucas y Fibonacci $L n$ y $F n$ de argumento imaginario.

Los polinomios de Chebyshev desplazados del primer y segundo tipo están relacionados con los polinomios de Chebyshev por

{displaystyle T_{n}^{*}(x)=T_{n}(2x-1),qquad U_{n}^{*}(x)=U_{n}(2x-1).}

Cuando el argumento del polinomio de Chebyshev satisface $2 x - 1 \in [-1, 1]$ el argumento del polinomio de Chebyshev desplazado satisface $x \in [0, 1]$ . De manera similar, se pueden definir polinomios desplazados para intervalos genéricos $[a, b]$ .

Alrededor de 1990, los términos "tercer tipo" y "cuarto tipo" entró en uso en relación con los polinomios de Chebyshev, aunque los polinomios denotados por estos términos tuvieron un desarrollo anterior bajo el nombre polinomios aerodinámicos. Según J. C. Mason y G. H. Elliott, la terminología "tercer tipo" y "cuarto tipo" se debe a Walter Gautschi, "en consulta con colegas en el campo de los polinomios ortogonales." Los polinomios de Chebyshev de tercer tipo se definen como

{displaystyle V_{n}(x)={frac {cos left(left(n+{frac {1}{2}}right)theta right)}{cos left({frac {theta }{2}}right)}}={sqrt {frac {2}{1+x}}}T_{2n+1}left({sqrt {frac {x+1}{2}}}right)}

y los polinomios de Chebyshev de cuarta clase se definen como

{displaystyle W_{n}(x)={frac {sin left(left(n+{frac {1}{2}}right)theta right)}{sin left({frac {theta }{2}}right)}}=U_{2n}left({sqrt {frac {x+1}{2}}}right),}

Donde ${displaystyle theta =arccos x}$ . En la literatura de la fécula ${displaystyle V_{n}(x)}$ y ${displaystyle W_{n}(x)}$ son denotados ${displaystyle t_{n}(x)}$ y ${displaystyle u_{n}(x)}$ . Las familias polinómicas $T_n(x)$ , $U_n(x)$ , ${displaystyle V_{n}(x)}$ , y ${displaystyle W_{n}(x)}$ son ortogonales con respecto a los pesos

{displaystyle left(1-x^{2}right)^{-1/2},quad left(1-x^{2}right)^{1/2},quad (1-x)^{-1/2}(1+x)^{1/2},quad (1+x)^{-1/2}(1-x)^{1/2}}

y son proporcionales a los polinomios Jacobi ${displaystyle P_{n}^{(alphabeta)}(x)}$ con

{displaystyle (alphabeta)=left(-{frac {1}{2}},-{frac {1}{2}}right),quad (alphabeta)=left({frac {1}{2}},{frac {1}{2}}right),quad (alphabeta)=left(-{frac {1}{2}},{frac {1}{2}}right),quad (alphabeta)=left({frac {1}{2}},-{frac {1}{2}}right).}

Las cuatro familias satisfacen la recurrencia ${displaystyle p_{n}(x)=2xp_{n-1}(x)-p_{n-2}(x)}$ con $p_{0}(x)=1$ , donde ${displaystyle p_{n}=T_{n}}$ , $U_{n}$ , $V_{n}$ , o $W_{n}$ , pero difieren según si $p_{1}(x)$ iguales $x$ , $2x$ , $2x-1$ , o $2x+1$ .

Contenido relacionado

Más resultados...