Poliedro estrellado

En geometría, un poliedro estrellado es un poliedro que tiene una cualidad repetitiva de no convexidad que le da una calidad visual similar a la de una estrella.

Existen dos tipos generales de poliedros estelares:

• Polyhedra que se autointerseca de una manera repetitiva.
• Concave polihedra de un tipo particular que alterna convex y vértices de concave o silla de montar de una manera repetitiva. Matemáticamente estas figuras son ejemplos de dominios estrella.

Los estudios matemáticos de poliedros estelares suelen centrarse en poliedros regulares y uniformes, o en poliedros duales de poliedros uniformes. Todas estas estrellas son del tipo que se autointersecta.

Los poliedros estrellados regulares son poliedros que se intersecan entre sí. Pueden tener caras que se intersecan entre sí o figuras con vértices que se intersecan entre sí.

Existen cuatro poliedros estrellados regulares, conocidos como poliedros de Kepler-Poinsot. El símbolo de Schläfli {p,q} implica caras con lados p y figuras de vértice con lados q. Dos de ellos tienen caras pentagrammáticas {5/2} y dos tienen figuras de vértice pentagrammáticas.

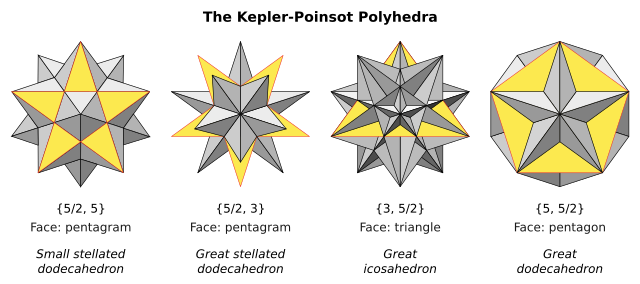
Estas imágenes muestran cada forma con una sola cara de color amarillo para mostrar la porción visible de esa cara.

Existe también un número infinito de diedros y hosoedros estelares regulares {2,p/q} y {p/q,2} para cualquier polígono estelar {p/q}. Si bien son degenerados en el espacio euclidiano, pueden realizarse esféricamente en forma no degenerada.

Existen numerosos poliedros estelares uniformes, entre los que se incluyen dos series infinitas, de prismas y antiprismas, y sus duales.

Los poliedros uniformes y dobles en estrella también son poliedros que se intersecan entre sí. Pueden tener caras que se intersecan entre sí, figuras de vértices que se intersecan entre sí o ambas cosas.

Los poliedros estrellados uniformes tienen caras regulares o caras de polígonos estrellados regulares. Los poliedros estrellados uniformes duales tienen caras regulares o figuras de vértices de polígonos estrellados regulares.

Ejemplo de polihedra uniforme y sus duales

Uniform polyhedron	Poliedro dual
El prisma pentagramamico es un poliedro estrella prismática. Se compone de dos caras pentagrama conectadas por cinco caras cuadradas intersectando.	La dipirámide pentagrama es también una estrella poliedron, representando el dual al prisma pentagramamico. Es face-transitive, compuesto por diez triángulos isosceles intersecting.
El gran dodecicosahedron es un poliedro estrella, construido a partir de una sola figura del vértice de la intersectación hexagonal y decagrammica, {10/3}, caras.	El gran dodecicosacrón es el dual al grandes dodecicosahedron. Es cara-transitiva, compuesta de 60 intersecciones pajarita- caras cuadrilaterales en forma.

Más allá de las formas anteriores, existen clases ilimitadas de poliedros autointersecantes (en forma de estrella).

Dos clases importantes son las estelaciones de poliedros convexos y sus duales, las facetas de los poliedros duales.

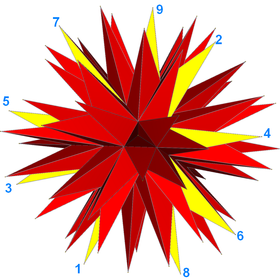
Por ejemplo, la estelación completa del icosaedro (ilustrada) puede interpretarse como un poliedro que se autointersecta compuesto por 20 caras idénticas, cada una de ellas un polígono enrollado (9/4). A continuación se muestra una ilustración de este poliedro con una cara dibujada en amarillo.

Un politopo que se intersecta a sí mismo de manera similar en cualquier número de dimensiones se denomina politopo estrella.

Un politopo regular {p,q,r,...,s,t} es un politopo estrella si su faceta {p,q,...s} o su figura de vértice {q,r,...,s,t} es un politopo estrella.

En cuatro dimensiones, las 10 policoras estelares regulares se denominan policoras de Schläfli–Hess. De manera análoga a los poliedros estelares regulares, estas 10 están compuestas por facetas que son uno de los cinco sólidos platónicos regulares o uno de los cuatro poliedros estelares regulares de Kepler–Poinsot.

Por ejemplo, la gran estrella de 120 celdas, proyectada ortogonalmente en el espacio tridimensional, se ve así:

No existen politopos estelares regulares de dimensiones superiores a 4.

Un poliedro que no se cruza consigo mismo, de modo que todo su interior puede verse desde un punto interior, es un ejemplo de dominio estelar. Las partes exteriores visibles de muchos poliedros estelares que se intersecan entre sí forman los límites de los dominios estelares, pero a pesar de su apariencia similar, como poliedros abstractos son estructuras diferentes. Por ejemplo, el pequeño dodecaedro estrellado tiene 12 caras de pentagrama, pero el dominio estelar correspondiente tiene 60 caras de triángulos isósceles y, en consecuencia, diferentes números de vértices y aristas.

Los dominios estelares poliédricos aparecen en varios tipos de arquitectura, generalmente de naturaleza religiosa. Por ejemplo, se ven en muchas iglesias barrocas como símbolos del Papa que construyó la iglesia, en iglesias húngaras y en otros edificios religiosos. Estas estrellas también se pueden utilizar como decoración. Las estrellas moravas se utilizan para ambos fines y se pueden construir en varias formas.

• Pológono estrella
• Stellation
• Compuesto poliedral
• List of uniform polyhedra
• Lista de polihedra uniforme por triángulo Schwarz

• Coxeter, H.S.M., M. S. Longuet-Higgins y J.C.P Miller, Uniform Polyhedra, Phil. Trans. 246 A (1954) pp. 401-450.
• Coxeter, H.S.M., Polytopes regulares3o. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (VI. Star-polyhedra, XIV. (pág. 263) [1]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (cap. 26, Regular star-polytopes, págs. 404 a 408)
• Tarnai, T., Krähling, J. y Kabai, S.; "Star polyhedra: from St. Mark's Basilica in Venice to Hungarian Protestant churches", Paper ID209, Proc. of the IASS 2007, Shell and Spatial Structures: Structural Architecture-Towards the Future Looking to the Past, University of IUAV, 2007. [2] Archivado 2010-11-29 en la máquina Wayback o [3]

• Weisstein, Eric W. "Star Polyhedron". MathWorld.