Plano de cuadrícula
En urbanismo, el plano cuadriculado, plano cuadriculado de calles o plano cuadriculado es un tipo de plano urbano en el que las calles discurren a ángulos rectos entre sí, formando una cuadrícula.
Dos características inherentes al plano de cuadrícula, intersecciones frecuentes y geometría ortogonal, facilitan el movimiento. La geometría ayuda con la orientación y la búsqueda de caminos y sus intersecciones frecuentes con la elección y la franqueza de la ruta a los destinos deseados.
En la antigua Roma, el método del plan de cuadrícula para medir la tierra se llamaba centuriación. El plano cuadriculado data de la antigüedad y se originó en múltiples culturas; algunas de las primeras ciudades planificadas se construyeron utilizando planos de cuadrícula en el subcontinente indio.
Historia
Planos de rejilla antiguos
Hacia el año 2600 a. C., Mohenjo-Daro y Harappa, las principales ciudades de la civilización del valle del Indo, se construyeron con manzanas divididas por una cuadrícula de calles rectas que iban de norte a sur y de este a oeste. Cada bloque estaba subdividido por pequeños carriles. Las ciudades y monasterios de Sirkap, Taxila y Thimi (en los valles del Indo y Katmandú), que datan del primer milenio a. C. al siglo XI d. C., también tenían diseños basados en cuadrículas.
Un trabajador' aldea (2570-2500 a. C.) en Giza, Egipto, albergaba una fuerza laboral rotativa y estaba distribuida en bloques de largas galerías separadas por calles en una cuadrícula formal. Muchas ciudades de culto piramidal usaban una orientación común: un eje norte-sur desde el palacio real y un eje este-oeste desde el templo, reuniéndose en una plaza central donde el Rey y Dios se unían y cruzaban.
Hammurabi, rey del imperio babilónico en el siglo XVIII a. C., ordenó la reconstrucción de Babilonia: construir y restaurar templos, murallas, edificios públicos y canales de irrigación. Las calles de Babilonia eran anchas y rectas, se cruzaban aproximadamente en ángulo recto y estaban pavimentadas con ladrillos y betún.
La tradición de los planos cuadriculados continúa en China desde el siglo XV a. C. en adelante en la planificación urbana tradicional de varios estados chinos antiguos. Las pautas puestas en forma escrita en el Kaogongji durante el período de primavera y otoño (770-476 a. C.) decían: "una ciudad capital debe ser cuadrada en el plano". Tres puertas a cada lado del perímetro conducen a las nueve calles principales que atraviesan la ciudad y definen su patrón de cuadrícula. Y por su trazado la ciudad debía tener la Corte Real situada al sur, la Plaza del Mercado al norte, el Templo Ancestral Imperial al este y el Altar a los Dioses de la Tierra y del Grano al oeste."
Teotihuacan, cerca de la actual Ciudad de México, es el sitio de planta cuadriculada antigua más grande de América. La cuadrícula de la ciudad cubría 21 kilómetros cuadrados (8 millas cuadradas).
Quizás el sistema de cuadrícula más conocido es el que se extendió por las colonias del Imperio Romano. La cuadrícula romana arquetípica fue introducida en Italia por primera vez por los griegos, y dicha información se transfirió a través del comercio y la conquista.
Antigua Grecia
Aunque la idea de la cuadrícula estaba presente en la planificación social y urbana helénica, no estaba generalizada antes del siglo V a. C. Sin embargo, lentamente ganó primacía a través del trabajo de Hippodamus de Mileto (498 - 408 a. C.), quien planeó y replanificó muchas ciudades griegas de acuerdo con esta forma. El concepto de cuadrícula como el método ideal de planificación urbana había sido ampliamente aceptado en la época de Alejandro Magno. Sus conquistas fueron un paso en la propagación del plan cuadriculado a lo largo de las colonias, algunas tan lejanas como Taxila en Pakistán, que más tarde se vería reflejada en la expansión del Imperio Romano. La cuadrícula griega tenía sus calles alineadas aproximadamente en relación con los puntos cardinales y, en general, buscaba aprovechar las señales visuales basadas en el paisaje montañoso típico de Grecia y Asia Menor. La cuadrícula de calles estaba formada por plateiai y stenophoi (equivalentes a los romanos decumani y cardines). Esto probablemente se ejemplificó mejor en Priene, en la actual Turquía occidental, donde la cuadrícula ortogonal de la ciudad se basaba en los puntos cardinales, en un terreno inclinado que creaba vistas hacia un río y la ciudad de Mileto.
Antigua Roma
El pueblo etrusco, cuyos territorios en Italia abarcaban lo que eventualmente se convertiría en Roma, fundó lo que ahora es la ciudad de Marzabotto a fines del siglo VI a. Su trazado se basó en las ideas jónicas griegas, y fue aquí donde se ubicaron los principales ejes este-oeste y norte-sur de una ciudad (el decumanus maximus y el cardo maximus respectivamente). se pudo ver por primera vez en Italia. Según Stanislawski (1946), los romanos utilizaron cuadrículas hasta finales de la República o principios del Imperio, cuando introdujeron la centuriación, un sistema que extendieron por el Mediterráneo y más tarde por el norte de Europa.
La expansión militar de este período facilitó la adopción de la forma de cuadrícula como estándar: los romanos establecieron castra (fuertes o campamentos) primero como centros militares; algunos de ellos se convirtieron en centros administrativos. La cuadrícula romana era similar en forma a la versión griega de una cuadrícula, pero permitía consideraciones prácticas. Por ejemplo, las castra romanas a menudo se ubicaban en terrenos llanos, especialmente cerca o en nodos importantes como cruces de ríos o intersecciones de rutas comerciales. Las dimensiones de la castra eran a menudo estándar, y cada una de sus cuatro paredes generalmente tenía una longitud de 660 metros (2150 pies). La familiaridad era el objetivo de tal estandarización: los soldados podían estar estacionados en cualquier lugar del Imperio, y la orientación sería fácil dentro de las ciudades establecidas si tuvieran un diseño estándar. Cada uno tendría en su centro los mencionados decumanus maximus y cardo maximus, y su intersección formaría el foro, alrededor del cual se ubicarían importantes edificios públicos. De hecho, tal era el grado de similitud entre las ciudades que Higgins afirma que los soldados "estarían alojados en la misma dirección cuando se trasladaron de castra a castra". Pompeya ha sido citada tanto por Higgins como por Laurence como el ejemplo mejor conservado de la cuadrícula romana.
Fuera de la castra, también se dividieron grandes extensiones de tierra de acuerdo con la cuadrícula dentro de las murallas. Por lo general, tenían 730 metros (2400 pies) por lado (llamados centuria) y contenían 100 parcelas de tierra (cada una llamada heredium). El decumanus maximus y el cardo maximus se extendían desde las puertas de la ciudad hacia los asentamientos vecinos. Estos se alinearon para ser lo más rectos posible, desviándose de su camino solo debido a obstáculos naturales que impedían una ruta directa.
Si bien la imposición de una sola forma de ciudad independientemente de la región podría verse como una imposición de la autoridad imperial, no hay duda del razonamiento práctico detrás de la formación de la cuadrícula romana. Bajo la guía romana, la cuadrícula fue diseñada para ser eficiente e intercambiable, lo que facilitó y ayudó a la expansión de su imperio.
Asia desde el primer milenio dC
A medida que Japón y la península de Corea se centralizaron políticamente en el siglo VII d. C., esas sociedades adoptaron los principios chinos de planificación de redes en numerosos lugares. En Corea, Gyeongju, la capital de Silla Unificada, y Sanggyeong, la capital de Balhae, adaptaron el modelo chino de la dinastía Tang. Las antiguas capitales de Japón, como Fujiwara-Kyô (694-710 d. C.), Nara (Heijô-Kyô, 710-784 d. C.) y Kioto (Heian-Kyô, 794-1868 d. C.) también se adaptaron de Tang's capital, Chang'an. Sin embargo, por razones de defensa, los planificadores de Tokio evitaron la cuadrícula y optaron por una red irregular de calles que rodeaban los terrenos del castillo de Edo. En períodos posteriores, algunas partes de Tokio se planificaron en cuadrícula, pero los planes de cuadrícula son generalmente raros en Japón y, en consecuencia, el sistema de direcciones japonés se basa en subdivisiones cada vez más finas, en lugar de una cuadrícula.
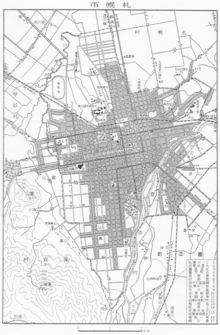
La tradición de planificación cuadriculada en Asia continuó hasta principios del siglo XX, con Sapporo, Japón (fundada en 1868) siguiendo un plan cuadriculado bajo la influencia estadounidense.
Europa y sus colonias (siglos XII-XVII)
Las nuevas ciudades europeas se planificaron utilizando cuadrículas a partir del siglo XII, de manera más prodigiosa en las bastidas del sur de Francia que se construyeron durante los siglos XIII y XIV. Las nuevas ciudades europeas medievales que usaban planes de cuadrícula estaban muy extendidas, desde Gales hasta la región florentina. Muchos fueron construidos sobre rejillas antiguas establecidas originalmente como puestos de avanzada coloniales romanos. En las Islas Británicas, el nuevo sistema de ciudad planificado que involucraba un diseño de calles en cuadrícula era parte del sistema de robo. Un ejemplo de una ciudad planificada medieval en los Países Bajos es Elburg. Bury St Edmunds es un ejemplo de una ciudad planificada en un sistema de cuadrícula a fines del siglo XI.
El modelo romano también se utilizó en los asentamientos españoles durante la Reconquista de Isabel y Fernando. Posteriormente se aplicó en las nuevas ciudades establecidas durante la colonización española de América, tras la fundación de San Cristóbal de La Laguna (Islas Canarias) en 1496. En 1573, el rey Felipe II de España compiló las Leyes de Indias para orientar la construcción y administración de comunidades coloniales. Las Leyes especificaban una plaza central cuadrada o rectangular con ocho calles principales que partían de las esquinas de la plaza. Cientos de comunidades cuadriculadas en todo el continente americano se establecieron de acuerdo con este patrón, haciéndose eco de las prácticas de las civilizaciones indias anteriores.
La capital barroca de Malta, La Valeta, que data del siglo XVI, se construyó siguiendo un plan de cuadrícula rígida de casas de diseño uniforme, salpicadas de palacios, iglesias y plazas.
El plano cuadriculado se hizo popular con el inicio del Renacimiento en el norte de Europa. En 1606, la ciudad recién fundada de Mannheim en Alemania fue la primera ciudad renacentista trazada en el plano cuadriculado. Más tarde vino la Ciudad Nueva de Edimburgo y casi todo el centro de la ciudad de Glasgow, y muchas comunidades y ciudades planificadas en Australia, Canadá y Estados Unidos.
Derry, construida entre 1613 y 1618, fue la primera ciudad planificada de Irlanda. El diamante central dentro de una ciudad amurallada con cuatro puertas se consideró un buen diseño para la defensa. El patrón de cuadrícula se copió ampliamente en las colonias de la América del Norte británica.
Rusia (siglo XVIII)
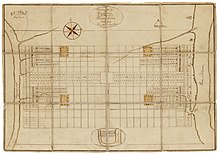
En Rusia, la primera ciudad planificada fue San Petersburgo, fundada en 1703 por Pedro I. Consciente de la experiencia de la construcción europea moderna que examinó en los años de su Gran Embajada en Europa, el Zar ordenó a Domenico Trezzini que elaborara la primera plano general de la ciudad. El proyecto de este arquitecto para Vasilyevsky Island era una típica cuadrícula de calles rectangulares (originalmente destinadas a ser canales, como en Amsterdam), con tres vías de circulación longitudinales, cruzadas rectangularmente con unas 30 calles transversales.
La forma de las cuadras de las calles en la isla Vasilyevsky es la misma que se implementó más tarde en el Proyecto de los Comisionados. Plano de 1811 para Manhattan: rectángulos alargados. El lado más largo de cada bloque da a la calle relativamente estrecha con un nombre numérico (en Petersburgo se llaman Liniya (Línea)), mientras que el lado más corto da a avenidas anchas. Para denotar avenidas en Petersburgo, se introdujo un término especial prospekt. Dentro de la cuadrícula de la isla Vasilyevsky hay tres prospekts, llamados Bolshoi (Grande), Sredniy (Medio) y Maly (Pequeño) mientras que los extremos de cada línea se cruzan con los terraplenes de los ríos Bolshaya Neva y Smolenka en el delta del río Neva.
La peculiaridad de las 'líneas' (calles) el nombre en esta cuadrícula es que cada lado de la calle tiene su propio número, por lo que una 'línea' es un lado de una calle, no toda la calle. La numeración tiene una base cero latente, sin embargo, la supuesta "línea cero" tiene su nombre propio Kadetskaya liniya, mientras que el lado opuesto de esta calle se llama '1-st Line'. La siguiente calle se llama '2-nd Line' en el lado este, y la '3ra Línea' en el lado occidental. Después de la reorganización de la numeración de casas en 1834 y 1858, los números de casas pares se usan en las líneas impares y, respectivamente, los números de casas impares se usan para las líneas pares. Los números máximos para 'líneas' en Petersburgo son las líneas 28-29.
Más tarde, a mediados del siglo XVIII, apareció otra cuadrícula de bloques rectangulares con las calles numeradas en la parte continental de la ciudad: 13 calles nombradas a partir de la '1-st Rota' hasta el '13-th Rota', donde las empresas (alemán: Rotte, ruso: рота) del Regimiento Izmaylovsky fueron localizados.
Primeros Estados Unidos (siglos XVII-XIX)
Muchas de las primeras ciudades de los Estados Unidos, como Boston, no comenzaron con un sistema de cuadrícula. Sin embargo, incluso en los días anteriores a la revolución, algunas ciudades vieron los beneficios de tal diseño. New Haven Colony, una de las primeras colonias de Estados Unidos, se diseñó con una pequeña cuadrícula de 9 cuadrados en su fundación en 1638. A mayor escala, Filadelfia se diseñó en una cuadrícula de calles rectilíneas en 1682: una de las primeras ciudades del norte Estados Unidos para utilizar un sistema de red. A instancias del fundador de la ciudad, William Penn, el agrimensor Thomas Holme diseñó un sistema de calles anchas que se cruzan en ángulo recto entre el río Schuylkill al oeste y el río Delaware al este, incluidas cinco plazas de zonas verdes dedicadas. Penn anunció este diseño ordenado como una salvaguardia contra el hacinamiento, los incendios y las enfermedades que asolaban las ciudades europeas. Holme diseñó una versión ideal de la cuadrícula, pero surgieron callejones dentro y entre bloques más grandes a medida que la ciudad tomaba forma. A medida que Estados Unidos se expandía hacia el oeste, la planificación urbana basada en cuadrículas modelada en el diseño de Filadelfia se volvería popular entre las ciudades fronterizas, haciendo que las cuadrículas fueran omnipresentes en todo el país.
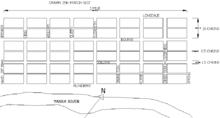
Otro plan de red muy conocido es el plan para la ciudad de Nueva York formulado en la Declaración de los Comisionados. Plan de 1811, una propuesta de la legislatura estatal de Nueva York para el desarrollo de la mayor parte de Manhattan por encima de Houston Street.
Washington, D.C., la capital de los Estados Unidos, fue planificada por el arquitecto franco-estadounidense Pierre Charles L'Enfant. Bajo el plan L'Enfant, el Distrito de Columbia original se desarrolló utilizando un plan de cuadrícula que se interrumpe por avenidas diagonales, la más famosa es la avenida Pennsylvania. Estas diagonales a menudo están conectadas por círculos de tráfico, como Dupont Circle y Washington Circle. A medida que la ciudad creció, el plan se duplicó para cubrir la mayor parte del resto de la capital. Mientras tanto, el centro de la ciudad enfrentó el desorden y se adoptó el Plan McMillan, dirigido por el Senador James McMillan, para construir un National Mall y un sistema de parques que aún hoy es una joya de la ciudad.
A menudo, algunas de las calles de una cuadrícula están numeradas (Primera, Segunda, etc.), con letras o ordenadas alfabéticamente. El centro de San Diego usa los tres esquemas: las calles de norte a sur están numeradas de oeste a este, y las calles de este a oeste están divididas entre una serie de letras que van hacia el sur de la A a la L y una serie de calles con nombres de árboles o plantas, que van hacia el norte alfabéticamente. del fresno al nogal. Como en muchas ciudades, algunas de estas calles han recibido nuevos nombres violando el sistema (la antigua Calle D ahora es Broadway, la antigua Avenida 12 ahora es Park Boulevard, etc.); esto ha significado que 2nd, no 1st, es el nombre de calle más común en los Estados Unidos.
Una excepción a la típica cuadrícula uniforme es el plan de Savannah, Georgia (1733), conocido como el Plan Oglethorpe. Es un bloque de ciudad celular compuesto que consta de cuatro bloques de esquina grandes, cuatro bloques pequeños en el medio y una plaza pública en el centro; toda la composición de aproximadamente diez acres (cuatro hectáreas) se conoce como barrio. Su estructura celular incluye todos los usos primarios del suelo de un barrio y por eso se le ha llamado fractal. Su configuración de calles presagia técnicas modernas de moderación del tráfico aplicadas a cuadrículas uniformes donde ciertas calles seleccionadas se vuelven discontinuas o estrechas, desincentivando así el tráfico. La configuración también representa un ejemplo de espacio compartido funcional, donde el tránsito de peatones y vehículos puede coexistir de manera segura y cómoda.
En el desarrollo hacia el oeste de los Estados Unidos, el uso del plano cuadriculado fue casi universal en la construcción de nuevos asentamientos, como en Salt Lake City (1870), Dodge City (1872) y Oklahoma City (1890). En estas ciudades occidentales, las calles se numeraron incluso con más cuidado que en el este para sugerir una futura prosperidad y estatus metropolitano.
Una de las principales ventajas del plan de cuadrícula era que permitía la rápida subdivisión y subasta de una gran parcela de tierra. Por ejemplo, cuando la legislatura de la República de Texas decidió en 1839 trasladar la capital a un nuevo sitio a lo largo del río Colorado, el funcionamiento del gobierno requirió la rápida población de la ciudad, que recibió el nombre de Austin. Encargado de la tarea, Edwin Waller diseñó una cuadrícula de catorce bloques frente al río en 640 acres (exactamente 1 milla cuadrada; aproximadamente 2,6 km2). Después de medir el terreno, Waller organizó la venta casi inmediata de 306 lotes y, para fines de año, todo el gobierno de Texas había llegado en carretas de bueyes al nuevo sitio. Aparte de la velocidad de la ventaja topográfica, la lógica en el momento de la adopción de la red en esta y otras ciudades sigue siendo oscura.
Principios del siglo XIX: Australasia
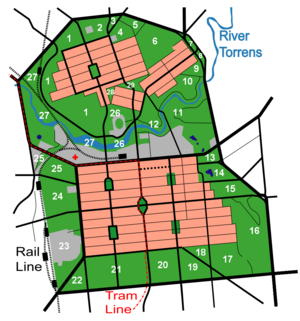
En 1836, William Light elaboró sus planos para Adelaida, en el sur de Australia, sobre el río Torrens. Dos áreas al sur (el centro de la ciudad) y al norte (North Adelaide) del río se diseñaron en un patrón de cuadrícula, con la ciudad rodeada por Adelaide Park Lands.
Hoddle Grid es el nombre que se le da al diseño de Melbourne, Victoria, en honor al topógrafo Robert Hoddle, quien lo trazó en 1837 al establecer el primer plano formal de la ciudad. Esta cuadrícula de calles, trazada cuando había solo unos pocos cientos de colonos, se convirtió en el núcleo de lo que ahora es una ciudad de más de 5 millones de personas, la ciudad de Melbourne. Las inusuales dimensiones de los huertos y la incorporación de estrechos 'pequeños' calles fueron el resultado del compromiso entre el deseo de Hoddle de emplear las regulaciones establecidas en 1829 por el anterior gobernador de Nueva Gales del Sur, Ralph Darling, que requería bloques cuadrados y calles anchas y espaciosas, y el deseo de Bourke de vías de acceso traseras (ahora las calles 'pequeñas', por ejemplo Little Collins Street).
La ciudad de Christchurch, Nueva Zelanda, fue planificada por Edward Jollie en 1850.
Acre de la ciudad
El término "acre de la ciudad" (a menudo escrito con letras mayúsculas iniciales) puede haberse originado con Edward Gibbon Wakefield, quien estuvo involucrado en varios esquemas para promover la colonización de Australia del Sur en la década de 1830 y, como fundador de New Zealand Company, los planes para Wellington, New Plymouth y Nelson. Todos estos pueblos estaban trazados en un plano cuadriculado, por lo que era fácil dividir la tierra en parcelas de un acre (aproximadamente 0,4 ha), y estas se conocieron como acres de pueblo. Adelaide se dividió en 1042 Town Acres. Los mapas que muestran las divisiones de los acres de la ciudad están disponibles para Adelaide, Nelson y Wellington.
Finales del siglo XIX hasta la actualidad
Ildefons Cerdà, ingeniero de caminos español, definió un concepto de urbanismo, basado en la retícula, que aplicó al Eixample de Barcelona. La red del Eixample introdujo elementos de diseño innovadores que fueron excepcionales en ese momento e incluso únicos entre los planes de red posteriores:
- un bloque muy grande que mide 113 por 113 m (371 por 371 pies), mucho más grande que los bloques antiguos de la ciudad y más grande que cualquier bloque romano, griego y sus mutaciones (ver dibujo abajo);
- a 20 m (66 pies) ancho de carretera (derecha) comparado con la mayoría de 3 m en la ciudad vieja;
- bloques cuadrados con esquinas truncadas; y
- carreteras principales, perpendicular y diagonal, de 50 m (160 pies) de ancho.
Estas innovaciones se basaron en motivos funcionales: el tamaño del bloque, para permitir la creación de un espacio abierto interior silencioso (60 m por 60 m) y permitir una amplia luz solar y ventilación en sus edificios perimetrales; la geometría rectilínea, las calles y bulevares anchos para sustentar una alta movilidad y las esquinas recortadas para facilitar el giro de carretas y autocares y particularmente de vehículos sobre rieles fijos.
En los mapas de las ciudades estadounidenses más grandes, las áreas del centro casi siempre son cuadrículas. Estas áreas representan las dimensiones originales del terreno de la ciudad fundada, generalmente alrededor de una milla cuadrada. Algunas ciudades expandieron la cuadrícula más lejos del centro, pero los mapas también muestran que, en general, a medida que aumenta la distancia desde el centro, emerge una variedad de patrones sin un orden perceptible en particular. En yuxtaposición a la cuadrícula, aparecen al azar. Estos nuevos patrones se han clasificado sistemáticamente y se han medido sus características de diseño.
En los Estados Unidos, el sistema de red se usó ampliamente en la mayoría de las principales ciudades y sus suburbios hasta la década de 1960. Sin embargo, durante la década de 1920, la rápida adopción del automóvil provocó el pánico entre los planificadores urbanos, quienes, basándose en la observación, afirmaron que los automóviles a alta velocidad eventualmente matarían a decenas de miles de niños pequeños por año. Aparentemente, en esta etapa temprana de la entrada del automóvil a la red, las calles de las principales ciudades del mundo fueron el escenario de una virtual 'masacre'. ya que la tasa de mortalidad en proporción a la población era más del doble de la tasa actual. En 2009, después de varias décadas de mejoras en la seguridad vial y una disminución continua en las muertes, se estima que 33,963 personas murieron en accidentes de tráfico automovilísticos y, según la Administración Nacional de Seguridad del Tráfico en las Carreteras, "Los accidentes automovilísticos son la causa principal de muerte para niños de 3 a 14 años." Los planificadores, por lo tanto, pidieron una "supermanzana" arreglo que minimizó el tráfico de automóviles y desalentó a los automóviles de viajar en cualquier cosa que no sean carreteras arteriales; los generadores de tráfico, como los complejos de apartamentos y las tiendas, estarían restringidos a los bordes de la supermanzana, a lo largo de la arteria. Este paradigma prevaleció entre 1930 y 1960, especialmente en Los Ángeles, donde los ejemplos notables incluyen Leimert Park (un ejemplo temprano) y Panorama City (uno del período tardío).
Un destacado urbanista del siglo XX, Lewis Mumford, criticó severamente algunas de las características de la cuadrícula: "Con un cuadrado en T y un triángulo, finalmente, el ingeniero municipal podría, sin la menor capacitación como un arquitecto o un sociólogo, 'plan' una metrópolis, con sus lotes estándar, sus bloques estándar, sus anchos de calle estándar, en una palabra, con sus partes estandarizadas, comparables y reemplazables. Los nuevos planes de parrilla fueron espectaculares en su ineficiencia y desperdicio. Al no poder discriminar lo suficiente entre las arterias principales y las calles residenciales, las primeras no se hicieron lo suficientemente anchas mientras que las segundas solían ser demasiado anchas para funciones puramente vecinales... en cuanto a su contribución a las funciones sociales permanentes de la ciudad, la parrilla anónima el plan resultó vacío."
En la década de 1960, los ingenieros de tráfico y los planificadores urbanos abandonaron la cuadrícula prácticamente en su totalidad a favor de una "jerarquía de calles". Este es un modelo completamente "asimétrico" disposición de calles en la que una subdivisión residencial, a menudo rodeada por un muro acústico o una puerta de seguridad, está completamente separada de la red vial, excepto por una o dos conexiones a vías arteriales. En cierto modo, se trata de un regreso a los estilos medievales: como se señala en la historia seminal del diseño urbano de Spiro Kostof, The City Shaped, existe un gran parecido entre la disposición de las calles de los modernos arrabales y los de las ciudades medievales árabes y moriscas. En cada caso, la unidad comunitaria en cuestión —el clan o la familia extendida en el mundo musulmán, la subdivisión económicamente homogénea en los suburbios modernos— se aísla de la escena urbana más amplia mediante el uso de callejones sin salida y culs-de-sac. yo>.
Milton Keynes
Un famoso sistema de cuadrícula se encuentra en la nueva ciudad británica de Milton Keynes. En esta ciudad planificada, que comenzó a construirse en 1967, un sistema de diez "horizontales" (aproximadamente de este a oeste) y once "vertical" Se utilizaron carreteras (aproximadamente de norte a sur), con rotondas en cada intersección. Todas las carreteras horizontales recibieron nombres que terminaban en 'camino' y números H (para 'horizontal', por ejemplo, H3 Monks Way). Los caminos verticales recibieron nombres que terminaban en 'calle' y números V (para 'vertical', por ejemplo, V6 Grafton Street). Cada camino de la cuadrícula estaba espaciado aproximadamente un kilómetro a lo largo del siguiente, formando cuadrados de aproximadamente un kilómetro cuadrado. Cada plaza y cada rotonda recibió su propio nombre. El sistema proporcionó un transporte muy fácil dentro de la ciudad, aunque confundió a los visitantes que no estaban familiarizados con el sistema. Los cuadrados de la cuadrícula así formados son mucho más grandes que las manzanas de la ciudad descritas anteriormente, y los diseños de las carreteras dentro de los cuadrados de la cuadrícula son generalmente 'orgánicos' en forma, coincidiendo con el modelo de jerarquía de calles descrito anteriormente.
Beneficios y críticas
Coste financiero
Ancho de la calle, o derecho de paso (ROW), influye en la cantidad de tierra que se dedica a las calles, que deja de estar disponible para el desarrollo y, por lo tanto, representa un costo de oportunidad. Cuanto más ancha sea la calle, mayor será el costo de oportunidad. El ancho de la calle está determinado por consideraciones estéticas y de circulación y no depende de la configuración del patrón. Cualquier configuración puede tener calles anchas o estrechas.
La longitud de la calle influye proporcionalmente en la cantidad de componentes de la calle que deben construirse, como pavimento, bordillos y aceras, alcantarillas y desagües pluviales, postes de luz y árboles. La longitud de la calle de un área determinada de desarrollo depende de la frecuencia con la que ocurren las calles, que a su vez depende de la longitud y el ancho de una cuadra. Cuanto mayor sea la frecuencia de las calles, mayor será su longitud total. Cuanto más pequeñas sean las dimensiones de la manzana, mayor será la frecuencia de las calles. A medida que aumenta la frecuencia de las calles, también lo hace el número de intersecciones. Las intersecciones normalmente cuestan más que la longitud de la calle recta porque requieren mucha mano de obra y requieren señalización de la calle y el tráfico.
El ancho del pavimento influye en el costo al afectar la cantidad de materiales y mano de obra necesarios para proporcionar una superficie de carretera terminada. El ancho del pavimento generalmente se basa en consideraciones de ingeniería de tráfico y no depende de la configuración del patrón. Al igual que con el ancho de la calle, cualquier patrón puede tener aceras anchas o estrechas. De los tres factores que afectan el costo, el ancho de la calle, la longitud de la calle y el ancho del pavimento, solo la longitud de la calle depende del patrón. Por lo tanto, una comparación objetiva de costos se basaría en esta variable con el pleno entendimiento de que las otras variables, aunque opcionales, pueden desempeñar un papel.
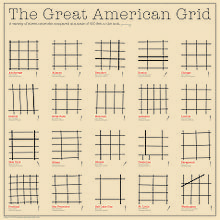
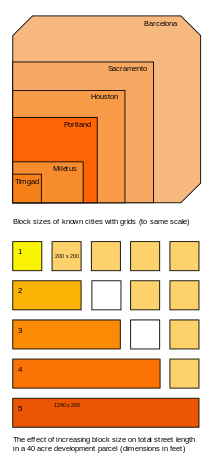
Los patrones de cuadrícula ortogonales tradicionales generalmente tienen mayores frecuencias de calles que los patrones discontinuos. Por ejemplo, el bloque de Portland es de 200 pies × 200 pies, mientras que el de Mileto es de 200 pies × 200 pies. es la mitad de ese tamaño y la mitad de Timgad otra vez (ver diagrama). Houston, Sacramento y Barcelona son progresivamente más grandes alcanzando hasta cuatro veces el área del bloque de Portland. El plan de 1811 de Nueva York (ver arriba) tiene bloques de 200 pies (61 m). de ancho y longitudes variables que van desde aproximadamente 500 pies (150 m) a 900 pies (270 m) pies. La frecuencia correspondiente de calles para cada uno de estos tamaños de bloque afecta la longitud de la calle.
Un ejemplo simple de un patrón de cuadrícula de calles (ver diagrama) ilustra la reducción progresiva en la longitud de la calle total (la suma de todas las longitudes de las calles individuales) y el aumento correspondiente en la longitud de las cuadras. Para una reducción correspondiente de una, dos, tres y cuatro calles dentro de esta parcela de 40 acres (16 ha), la longitud de la calle se reduce de un total original de 12,600 pies (3,800 m) a 7,800 pies (2,400 m) pies lineales, una reducción del 39%. Simultáneamente, las longitudes de los bloques aumentan de 200 × 200 pies a 1240 × 200 pies. Cuando los cinco bloques alcanzaron el tamaño final de 1240 pies (380 m), se eliminaron cuatro tramos de calle de un total de ocho. Los bloques de 300 m (1000 pies) o más de longitud rara vez aparecen en los planos de cuadrícula y no se recomiendan, ya que obstaculizan el movimiento de los peatones (peatones, a continuación). Desde la perspectiva del peatón, cuanto más pequeña es la manzana, más fácil es la navegación y más directa la ruta. En consecuencia, se prefieren las rejillas más finas.
Los patrones que incorporan tipos de calles discontinuas, como medias lunas y callejones sin salida, en general, no han considerado el movimiento de peatones como una prioridad y, en consecuencia, han producido bloques que generalmente están en el rango de 1,000 pies (300 m) y a menudo lo superan. Como resultado, la frecuencia de las calles cae y también lo hace la longitud total de las calles y, por lo tanto, el costo. En general, no es el patrón de calles per se lo que afecta los costos, sino la frecuencia de las calles que necesita o incorpora a propósito.
Una ventaja inherente de la geometría ortogonal de una cuadrícula adecuada es su tendencia a generar lotes regulares en secuencias bien empaquetadas. Esto maximiza el uso de la tierra del bloque; sin embargo, no afecta la frecuencia de las calles. Cualquier frecuencia de calles ortogonales produce el mismo efecto de empaquetamiento. La geometría ortogonal también minimiza las disputas sobre los límites de los lotes y maximiza la cantidad de lotes que podrían estar frente a una calle determinada. John Randal dijo que el plan de red de Manhattan facilitó la 'compra, venta y mejora de bienes raíces'.
Otro aspecto importante de las cuadrículas de calles y el uso de bloques rectilíneos es que los flujos de tráfico de peatones, automóviles o ambos, solo se cruzan en ángulo recto. Esta es una característica importante de seguridad vial, ya que nadie que ingrese a la intersección necesita mirar por encima del hombro para ver el tráfico que se aproxima. Cada vez que los flujos de tráfico se encuentran en un ángulo agudo, nadie puede ver el tráfico que se les acerca. La cuadrícula es, por lo tanto, una respuesta geométrica a nuestra fisiología humana. Es muy probable que el propósito original de los diseños de cuadrícula provenga del Ágora ateniense. Antes de la organización de la red, los mercados se disponían al azar en un campo con enfoques de tráfico en ángulos extraños. Esto provocó que los carros y vagones se volcaran debido a las frecuentes colisiones. La disposición de los puestos del mercado en filas regularizadas en ángulo recto resolvió este problema y luego se incorporó al Ágora ateniense y se copió desde entonces.
Características ecológicas, absorción de agua de lluvia y generación de contaminantes
Las rejillas uniformes típicas no responden a la topografía. El plan de Priene, por ejemplo, está ubicado en la ladera de una colina y la mayoría de sus calles de norte a sur están escalonadas, una característica que las habría hecho inaccesibles para carretas, carros y animales cargados. Muchas ciudades modernas, como San Francisco, Vancouver y Saint John, New Brunswick, siguen el ejemplo de Priene. En un contexto moderno, las pendientes pronunciadas limitan la accesibilidad en automóvil, y más aún en bicicleta, a pie o en silla de ruedas, particularmente en climas fríos.
La misma inflexibilidad de la cuadrícula conduce a ignorar áreas ambientalmente sensibles, como pequeños arroyos y arroyos o lotes de bosques maduros, en lugar de la aplicación de la geometría inmutable. Se dice del plan de red de Nueva York que aplastó todos los obstáculos en su camino. Por el contrario, los patrones de calles discontinuas recientes siguen la configuración de las características naturales sin alterarlas. La cuadrícula representa una solución racionalista y reduccionista a un problema multifacético.
Las frecuencias inherentes de calles principales e intersecciones de la cuadrícula producen grandes áreas de superficies impermeables en el pavimento de la calle y las aceras. En comparación con las redes recientes con tipos de calles discontinuas, las cuadrículas pueden ser hasta un 30% más altas en superficies impermeables atribuibles a las carreteras. La prioridad ambiental emergente de retener hasta el 90% del agua de lluvia en el sitio se vuelve problemática con altos porcentajes de superficies impermeables. Y dado que las carreteras constituyen la mayor parte de las superficies impermeables totales de un desarrollo, la dificultad se ve agravada por el tipo de diseño de cuadrícula. Por estas razones, los planificadores modernos han intentado modificar la cuadrícula clásica, rígida y uniforme.
Algunas ciudades, especialmente Seattle, han ideado medios para mejorar la capacidad de retención de una calle. Sin embargo, las intersecciones frecuentes, tal como ocurren en una cuadrícula regular, supondrían un obstáculo para su aplicación efectiva.
Un patrón de red de calles puede afectar la producción de contaminantes por la cantidad de viajes en automóvil que requiere y la velocidad a la que pueden viajar los automóviles. El plan de cuadrícula con sus intersecciones frecuentes puede desplazar una parte de los viajes locales en automóvil por caminar o andar en bicicleta debido a la franqueza de la ruta que ofrece a los peatones. Pero, mientras los autos también estén permitidos en esas calles, hace que las mismas rutas sean más directas para los autos, lo que podría ser un incentivo para conducir. El desplazamiento potencial del viaje en automóvil resultaría en una reducción de las emisiones contaminantes. La ventaja de la densidad de las intersecciones para los peatones, sin embargo, puede tener un efecto contrario para los automóviles debido a su potencial para reducir la velocidad. Las velocidades bajas inferiores a 32 km/h (20 mph) tienen un coeficiente de producción de contaminantes significativamente mayor que las superiores a 48 km/h (30 mph), aunque el coeficiente después de estabilizarse tiende a aumentar gradualmente después de 80 km/h (50 mph). Este efecto se acentúa con una alta densidad de tráfico en áreas con usos comerciales donde las velocidades se reducen. Dado que el plan de cuadrícula no es jerárquico y las intersecciones son frecuentes, todas las calles pueden estar sujetas a esta reducción potencial de velocidades promedio, lo que lleva a una alta producción de contaminantes. Los gases de efecto invernadero y nocivos pueden ser perjudiciales para el medio ambiente y para la salud de los residentes.
Entorno social y seguridad
En su estudio seminal de 1982 sobre calles habitables que se llevó a cabo en vecindarios con cuadrícula, Donald Appleyard demostró que las redes sociales y los juegos callejeros se degradaban a medida que aumentaba el tráfico en una calle. Su investigación sentó las bases para la moderación del tráfico y para varias iniciativas, como calles vivas y Zonas de Hogar, todas las cuales tienen como objetivo mejorar el entorno social de una calle. La cantidad de tráfico en una calle depende de variables como la densidad de población del barrio, la propiedad de automóviles y su proximidad a edificios comerciales, institucionales o recreativos. Sin embargo, lo más importante es que depende de si una calle es o podría convertirse en un camino directo hacia un destino. Como vía de paso, podría soportar niveles impredecibles de tráfico que pueden fluctuar durante el día y aumentar con el tiempo.
Una característica clave del patrón de cuadrícula es que todas y cada una de las calles son igualmente accesibles para el tráfico (no jerárquicas) y pueden elegirse a voluntad como rutas alternativas a un destino. Los residentes se han resistido a conducir por cortes o atajos. Las ciudades respondieron haciendo modificaciones para evitarlo. La práctica de diseño actual recomendada sugiere el uso de intersecciones de 3 vías para aliviarlo.
La geometría de la cuadrícula abierta normal es evidentemente inadecuada para proteger o mejorar el entorno social de una calle de la influencia negativa del tráfico. De manera similar, un estudio innovador de 1972 de Oscar Newman sobre una teoría del espacio defendible describió formas de mejorar el entorno social y la seguridad de los vecindarios y las calles. En una aplicación práctica de su teoría en Five Oaks, el patrón de cuadrícula del vecindario se modificó para evitar el tráfico y crear enclaves más pequeños identificables mientras se mantiene la libertad total de movimiento de los peatones. El resultado positivo de estos cambios refuerza los hallazgos de Appleyard y la necesidad de reducir o prevenir el tránsito en las calles de los vecindarios; una necesidad que no se puede satisfacer con una cuadrícula típica, uniforme y abierta.
La cuestión de la seguridad del vecindario ha sido un foco constante de investigación desde el trabajo de Oscar Newman. Una nueva investigación ha ampliado la discusión sobre este tema en disputa. Un estudio reciente realizó un extenso análisis espacial y correlacionó varios edificios, planos del sitio y factores sociales con las frecuencias delictivas e identificó matices sutiles en las posiciones contrastantes. El estudio analizó, entre otros, los tipos de vivienda, la densidad unitaria (densidad de sitio), el movimiento en la calle, los callejones sin salida o las cuadrículas y la permeabilidad de un área residencial. Entre sus conclusiones se encuentran, respectivamente, que los pisos son siempre más seguros que las casas y la riqueza de los habitantes importa, la densidad es beneficiosa en general pero más a nivel del suelo, el movimiento local es beneficioso, pero no el de mayor escala, la riqueza relativa y el número de vecinos tener un efecto mayor que estar en un callejón sin salida o estar en una calle de paso. También restableció que los callejones sin salida simples y lineales con un buen número de viviendas unidas a través de calles tienden a ser seguros. En cuanto a la permeabilidad, sugiere que las áreas residenciales deberían ser lo suficientemente permeables para permitir el movimiento en todas las direcciones, pero no más. La provisión excesiva de permeabilidad mal utilizada es un peligro delictivo. La rejilla abierta y uniforme podría verse como un ejemplo de permeabilidad indiferenciada.
Un estudio reciente en California examinó la cantidad de juegos infantiles que ocurrían en las calles de vecindarios con diferentes características; patrón de cuadrícula y callejones sin salida. Los hallazgos indican que las calles de cuadrícula abierta mostraron una actividad de juego sustancialmente menor que el tipo de calle sin salida. Los callejones sin salida reducen el peligro percibido del tráfico y, por lo tanto, fomentan más juegos al aire libre. Señaló el camino hacia el desarrollo de patrones de redes de calles híbridas que mejoran el movimiento de los peatones pero restringen la conducción por cortes directos. Estudios similares en Europa y más recientemente en Australia encontraron que el juego al aire libre de los niños se reduce significativamente en las carreteras donde el tráfico es, o los padres lo perciben, como un riesgo. Como resultado de esta percepción errónea del riesgo, los niños que viven en comunidades sin salida tienen más probabilidades de morir atropellados por vehículos. Este mayor riesgo de muerte se debe a múltiples factores, que incluyen a las familias que manejan distancias más largas para llegar a sus destinos, los padres dedican menos tiempo a enseñar a sus hijos a tener cuidado con el tráfico y un mayor riesgo de que los padres atropellen accidentalmente a los niños en sus vehículos. "seguro" calzadas y calles sin salida.
Actividades tradicionales en la calle, como actividades infantiles' jugar, pasear y socializar son incompatibles con el flujo de tráfico, que fomenta la geometría de cuadrícula abierta y uniforme. Por estas razones, ciudades como Berkeley, California y Vancouver, Columbia Británica, entre muchas otras, transformaron calles residenciales existentes que formaban parte de un plan de cuadrícula en callejones sin salida permeables y conectados. Esta transformación conserva la permeabilidad y la conectividad de la red para los modos de transporte activos, pero filtra y restringe el tráfico de automóviles en la calle sin salida únicamente a los residentes.
Movimiento de peatones y bicicletas
Las redes de calles de ciudades antiguas que crecieron orgánicamente, aunque admiradas por ser pintorescas, pueden resultar confusas para los visitantes, pero rara vez para los habitantes originales (ver plano). Similarmente confusos para los visitantes son los planos de subdivisiones modernas con calles discontinuas y curvilíneas. El cambio de orientación de la calle, particularmente cuando es gradual o arbitrario, no se puede "mapear" en la mente. Los callejones sin salida, las medias lunas o los callejones sin salida frustran al viajero, especialmente cuando son largos, obligando a un arduo volver sobre sus pasos.
La frecuencia de las intersecciones, sin embargo, también se convierte en una desventaja para los peatones y las bicicletas. Interrumpe el galope relajado de la marcha y obliga a los peatones a salir a la calzada, un territorio hostil que genera ansiedad. Las personas con limitaciones físicas o debilidades, como los niños y las personas mayores, por ejemplo, pueden encontrar un desafío para caminar con regularidad. Para las bicicletas esta desventaja se acentúa ya que su velocidad normal es al menos el doble que la de los peatones. Las paradas frecuentes anulan la ventaja de la velocidad y el beneficio físico de andar en bicicleta y aumentan la frustración. Las intersecciones no solo son desagradables sino también peligrosas. La mayoría de las colisiones de tráfico y las lesiones ocurren en las intersecciones y la mayoría de las lesiones de los peatones que cruzan con el derecho de paso.
Surge un dilema al tratar de cumplir objetivos de planificación importantes cuando se usa la red: peatones, rentabilidad y responsabilidad ambiental. Para atender bien a los peatones, la ruta preferida es una configuración rectangular y una alta frecuencia de calles e intersecciones, que proporciona la geometría de cuadrícula ortogonal. Para reducir los costos de desarrollo y el impacto ambiental, una menor frecuencia de calles es el camino lógico. Dado que estos dos objetivos de diseño son contradictorios, es necesario lograr un equilibrio. Tal equilibrio se ha logrado en proyectos modernos líderes como Vauban, Freiburg y Village Homes, Davis. Ambos obtienen un puntaje alto en la participación del modo de peatones y bicicletas y, al mismo tiempo, en la reducción de las externalidades negativas del desarrollo. Sus configuraciones de diseño representan una fusión del plan de cuadrícula clásico con patrones de red de calles recientes.
Al examinar el tema de la transitabilidad, una comparación reciente de siete diseños de vecindarios encontró un aumento del 43 y 32 por ciento en caminar con respecto a un plan de cuadrícula y un diseño suburbano convencional en un diseño de cuadrícula fusionada, que tiene una mayor permeabilidad para los peatones que para los automóviles. debido a su inclusión de caminos peatonales dedicados. También mostró un rango de 7 a 10 por ciento de reducción en la conducción con respecto a los seis diseños de vecindario restantes en el conjunto, un beneficio ambiental.
Seguridad
La seguridad percibida y real juegan un papel en el uso de la calle. La seguridad percibida, aunque tal vez sea un reflejo inexacto de la cantidad de lesiones o muertes, influye en la actitud de los padres. decisión de permitir que sus hijos jueguen, caminen o anden en bicicleta en la calle. Los niveles reales de seguridad medidos por el número total de colisiones y el número y la gravedad de las lesiones son un asunto de interés público. Ambos deben informar el diseño, si se quiere que la red de calles logre su uso óptimo.
Estudios recientes han encontrado tasas más altas de accidentes de tránsito en las áreas suburbanas periféricas que en las ciudades centrales y los suburbios del interior con bloques más pequeños y patrones de calles más conectados. Si bien parte de esta disparidad es el resultado de la distancia de las instalaciones médicas de emergencia (los hospitales generalmente se construyen en una etapa bastante tardía del desarrollo de un área suburbana), está claro que las velocidades más bajas fomentadas por la frecuencia de las intersecciones disminuyen la gravedad de los accidentes ocurridos en calles dentro de un plan de cuadrícula.
Un estudio anterior encontró diferencias significativas en los accidentes registrados entre los vecindarios residenciales que estaban dispuestos en una cuadrícula y los que incluían callejones sin salida y medias lunas. La frecuencia de accidentes fue significativamente mayor en los barrios de la red.
Dos estudios más recientes examinaron la frecuencia de las colisiones en dos distritos regionales utilizando las últimas herramientas analíticas. Investigaron la posible correlación entre los patrones de la red de calles y la frecuencia de las colisiones. En un estudio, las redes cul-de-sac parecían ser mucho más seguras que las redes grid, en casi tres a uno. Un segundo estudio encontró que el plan de cuadrícula es el menos seguro por un margen significativo con respecto a todos los demás patrones de calles.
Un estudio de 2009 sugiere que los patrones de uso del suelo juegan un papel importante en la seguridad del tráfico y deben considerarse junto con el patrón de la red. Mientras que todos los tipos de intersecciones en general reducen la incidencia de choques fatales, las intersecciones de cuatro vías, que ocurren regularmente en una cuadrícula, aumentan significativamente los choques totales y con lesiones. El estudio recomienda redes de calles híbridas con densas concentraciones de intersecciones en T y concluye que no es deseable volver a la parrilla del siglo XIX.
La adherencia estricta al plan de cuadrícula puede causar fuertes pendientes ya que no se tiene en cuenta la topología del terreno. Esto puede ser peligroso para los conductores, peatones y bicicletas, ya que es más difícil controlar la velocidad y el frenado, especialmente en condiciones invernales.
Reconstrucción y desarrollo
Una de las mayores dificultades con los planes de cuadrícula es su falta de especialización, la mayoría de los servicios importantes se concentran a lo largo de las arterias principales de la ciudad. A menudo, los planos de cuadrícula se encuentran en asentamientos lineales, con una calle principal que conecta las carreteras perpendiculares. Sin embargo, esto se puede mitigar al permitir el desarrollo de uso mixto para que los destinos estén más cerca de casa. Muchas ciudades, especialmente en América Latina, aún conservan con éxito sus planes de red. Recientemente, los planificadores de los Estados Unidos y Canadá han revisado la idea de reintroducir patrones de cuadrícula en muchas ciudades y pueblos.
Ciudades y pueblos con un plano cuadriculado
América del Norte
Estados Unidos
- Austin
- Anniston, Alabama
- Atlanta
- Birmingham, Alabama
- Cedar Falls, Iowa
- Charlotte, Carolina del Norte
- Chicago
- Cincinnati
- Columbia, South Carolina
- Columbus, Ohio
- Dallas
- Detroit
- Fresno, California
- Holyoke
- Houston
- Indianapolis
- Jacksonville
- Los Ángeles
- Lake Charles, Louisiana
- Lubbock
- Manchester
- Miami
- Milwaukee
- Minneapolis
- New Haven
- Ciudad de Nueva York (ver Plan de Comisionados de 1811)
- Oklahoma City
- Omaha, Nebraska
- Orlando
- Panorama City
- Phoenix
- Portland, Oregon
- Philadelphia
- Providence, Rhode Island
- Raleigh
- Richmond
- Sacramento
- Salt Lake City
- San Diego
- San Francisco
- San Jose, California
- Seattle (ver el diseño de la calle de Seattle)
- Savannah, Georgia (véase el Plan Oglethorpe)
- St. Louis
- San Petersburgo, Florida
- Tampa
- Traverse City
- Tucson
- Tulsa, Oklahoma
- Washington D.C. (ver Plan L'Enfant)
- Wichita, Kansas
- Wilmington, Delaware
- Wilmington, Carolina del Norte
- Windermere
- Winter Park, Florida
Canadá
- Calgary
- Edmonton
- Halifax
- Hamilton
- London, Ontario
- Montreal
- Oshawa, Ontario
- Ottawa
- Quebec City, Quebec
- Regina
- San Juan
- Saskatoon
- Sudbury, Ontario
- Thunder Bay, Ontario
- Toronto (ver carretera de concesión)
- Vancouver
- Windsor
- Winnipeg
- Victoria
México
- Ciudad de México
- Puebla
América del Sur
Argentina
- Buenos Aires
- Mar del Plata
- Bahía Blanca
Chile
- Santiago
Perú
- Lima
Europa
España
- Barcelona (ver Eixample and Pla Cerdà)
- Madrid (ver Plan Castro)
- Valencia (ver Eixample, Valencia)
- Donostia
Reino Unido
- Bury St Edmunds (rejilla medieval)
- Derry
- Glasgow
- Manchester
- Middlesbrough
- Milton Keynes (ver sistema de carreteras de red Milton Keynes)
- New Town, Edimburgo
- Plymouth
- Winchelsea
Suiza
- La Chaux-de-Fonds
Italia
- Nápoles
- Turín
- Milán, parcialmente con el plan Beruto
- Reggio Calabria
- Messina
Irlanda
- Newtown Pery, Limerick
Malta
- Valletta
Países Bajos
- Elburg
- La Haya
- Nieuw-Vennep
Serbia
- Kraljevo
Finlandia
- Pori
Alemania
- Mannheim
Bulgaria
- Stara Zagora
- Byala Slatina
Oceanía
Australia
- Adelaida (ver Visión de la Luz)
- Ballarat
- Ballina
- Cairns
- Hobart
- Melbourne (ver Hoddle Grid)
- Newcastle, New South Wales (véase Dangar Grid)
- Perth en muchos de los suburbios internos más antiguos.
- Los suburbios de Sydney de Smithfield, Austral, Auburn y Canley Heights en el mayor oeste
Nueva Zelanda
- Christchurch
- Invercargill
África
Egipto
- Alexandria
Senegal
- Dakar
Somalia
- Mogadishu
Sudáfrica
- Ciudad del Cabo
- Johannesburgo
Asia
Japón
- Kyoto
- Nagoya
- Sapporo
India
- Amaravati
- Chandigarh
- Gandhinagar
- Jaipur
- Mulund, un suburbio de Mumbai
- Neyveli Township
China
- Beijing
- Datong
- Hong Kong (principalmente la península de Kowloon)
- Xi'an
Indonesia
- Batam
- Gilimanuk
- Kenyam
- Kolaka
- Lubuk Pakam
- Medan
- Metro
- Nabire
- North Yakarta
- Palangka Raya
- Pematangsiantar
- Pinrang
- Pontianak
- Siak Sri Indrapura
- Sibolga
- Sragen
- Surabaya
- Waingapu
- Wonogiri
- Pueblos y aldeas de los resultados del programa de transmigración en todo Indonesia
Israel
- Old Beersheba
Malasia
- Batu Pahat
- Ipoh
- Kota Kinabalu
- Muar
- Subang Jaya
- Taiping
Pakistán
- Islamabad
- Karachi
- Jauharabad
Filipinas
- Bacolod
- Banga
- Basco, Batanes
- Bonifacio Global City
- Butuan
- Candelaria
- Candon
- Cebu City
- Claveria, Cagayan
- Kidapawan
- Koronadal
- Lucena
- Intramuros, Manila
- Magalang
- Muñoz
- Pasay
- San Nicolas
- Santiago
- Tagum
- Tuguegarao
- Victoria
- Vigan
Singapur
- Punggol como rejilla fundida
- Anchorvale como rejilla fundida
Emiratos Árabes Unidos
- Abu Dhabi
- Dubai
- Sharjah
Vietnam
- Distrito 1, Ciudad Ho Chi Minh
Contenido relacionado
Río columbia
Océano de tetis
Río Brahmaputra