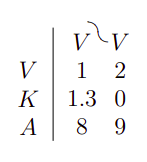Plankalkül

Plankalkül (Pronunciación alemana: [ˈplaːnkalkyːl]) es un lenguaje de programación diseñado con fines de ingeniería por Konrad Zuse entre 1942 y 1945. Fue el primer lenguaje de programación de alto nivel diseñado para una computadora.

Kalkül es el término alemán para un sistema formal, como en Hilbert-Kalkül, el nombre original del sistema de deducción al estilo de Hilbert, así que Plankalkül se refiere a un sistema formal de planificación.

Historia de la programación

En el dominio de la creación de máquinas informáticas, Zuse fue autodidacta y las desarrolló sin conocer otras máquinas informáticas mecánicas que ya existían, aunque más tarde (construyendo el Z3) se inspiró en las de Hilbert y Ackermann. 39;s libro sobre lógica matemática elemental (cf. Principios de Lógica Matemática). Para describir circuitos lógicos, Zuse inventó su propio diagrama y sistema de notación, al que llamó "combinatoria de condicionales" (Alemán: Bedingungskombinatorik). Después de terminar el Z1 en 1938, Zuse descubrió que el cálculo que había ideado de forma independiente ya existía y se conocía como cálculo proposicional. Lo que Zuse tenía en mente, sin embargo, necesitaba ser mucho más poderoso (el cálculo proposicional no es Turing-completo y no puede describir ni siquiera cálculos aritméticos simples). En mayo de 1939 describió sus planes para el desarrollo de lo que se convertiría en Plankalkül. Escribió lo siguiente en su cuaderno:

Mesa en casa en Hinterstein[de] donde Zuse trabajaba en Plankalkül

Mientras trabajaba en su tesis doctoral, Zuse desarrolló el primer sistema formal conocido de notación de algoritmos capaz de manejar bifurcaciones y bucles. En 1942 comenzó a escribir un programa de ajedrez en Plankalkül. En 1944, Zuse se reunió con el lógico y filósofo alemán Heinrich Scholz, quien expresó su aprecio por la utilización del cálculo lógico por parte de Zuse. En 1945, Zuse describió Plankalkül en un libro inédito. Sin embargo, el colapso de la Alemania nazi le impidió presentar su manuscrito.

En ese momento, las únicas dos computadoras que funcionaban en el mundo eran ENIAC y Harvard Mark I, ninguna de las cuales usaba un compilador, y ENIAC necesitaba ser reprogramada para cada tarea cambiando la forma en que se conectaban los cables.

Aunque la mayoría de sus computadoras fueron destruidas por las bombas aliadas, Zuse pudo rescatar una máquina, la Z4, y trasladarla al pueblo alpino de Hinterstein (parte de Bad Hindelang).

El primer intento de diseñar un lenguaje algorítmico fue emprendido en 1948 por K. Zuse. Su notación es bastante general, pero la propuesta nunca alcanzó la consideración que merece.

—Heinz Rutishauser, creador de ALGOL

Incapaz de continuar construyendo computadoras, lo que también estaba prohibido por las potencias aliadas, Zuse dedicó su tiempo al desarrollo de un modelo y lenguaje de programación de alto nivel. En 1948 publicó un artículo en el Archiv der Mathematik y lo presentó en la Reunión Anual del GAMM. Su trabajo no logró atraer mucha atención. En una conferencia de 1957, Zuse expresó su esperanza de que Plankalkül, "después de un tiempo como la Bella Durmiente, cobre vida". Expresó su decepción porque los diseñadores de ALGOL 58 nunca reconocieron la influencia de Plankalkül en su propio trabajo.

Plankalkül se publicó de forma más completa en 1972. Joachim Hohmann implementó el primer compilador en su disertación de 1975. Otras implementaciones independientes siguieron en 1998 y 2000 en la Universidad Libre de Berlín.

Descripción

Plankalkül ha establecido comparaciones con el lenguaje APL y con el álgebra relacional. Incluye sentencias de asignación, subrutinas, sentencias condicionales, iteración, aritmética de punto flotante, arreglos, estructuras de registros jerárquicos, aserciones, manejo de excepciones y otras funciones avanzadas, como la ejecución dirigida a objetivos. Plankalkül proporciona una estructura de datos llamada grafo generalizado (verallgemeinerter Graph), que se puede utilizar para representar estructuras geométricas.

Plankalkül compartió una notación idiosincrásica usando varias líneas con el Begriffsschrift de Frege de 1879 (que trata sobre lógica matemática).

Algunas características del Plankalkül:

• sólo variables locales
• funciones no soportan la recursión
• sólo admite llamadas por valor
• tipos compuestos son arrays y tuples
• contiene expresiones condicionales
• contiene un bucle y un bucle de tiempo
• No tengo

Tipos de datos

El único tipo de datos primitivos en el Plankalkül es un solo bit o booleano (alemán: Ja-Nein-Werte – no valor en la terminología de Zuses). Es denotado por el identificador S0{displaystyle S0}. Todos los tipos de datos adicionales son compuestos, y se acumulan desde primitivos por medio de "arrays" y "records".

Por lo tanto, una secuencia de ocho bits (que en la computación moderna podría ser considerado como byte) se denota por 8× × S0{displaystyle 8times S0}, y matriz booleana de tamaño m{displaystyle m} por n{displaystyle n}se describe por m× × n× × S0{displaystyle mtimes ntimes S0}. También existe una notación acortada, por lo que uno podría escribir S1⋅ ⋅ n{displaystyle S1cdot n} en lugar de n× × S0{displaystyle ntimes S0}.

Tipo S0{displaystyle S0} podría tener dos valores posibles 0{displaystyle 0} y L{displaystyle L.. Así que la secuencia de 4 bits podría ser escrita como L00L, pero en los casos en que tal secuencia representa un número, el programador podría utilizar la representación decimal 9.

Registro de dos componentes σ σ {displaystyle sigma } y τ τ {displaystyle tau } está escrito como ()σ σ ,τ τ ){displaystyle (sigmatau)}.

Tipo (alemán: Arte) en Plankalkül consta de 3 elementos: valor estructurado (alemán: Struktur), significado pragmático (alemán: Typ) y posible restricción a los posibles valores (alemán: Beschränkung). Los tipos definidos por el usuario se identifican por letra A con número, como A1{displaystyle A1} – primer tipo definido por el usuario.

Ejemplos

Zuse usó muchos ejemplos de la teoría del ajedrez:

A1{displaystyle A1}	S1⋅ ⋅ 3{displaystyle S1cdot 3}	Coordenada de tablero de ajedrez (tiene tamaño 8x8 por lo que 3 bits son lo suficiente)
A2{displaystyle A2}	2× × A1{displaystyle 2times A1}	cuadrado de la tabla (por ejemplo L00, 00L denota e2 en notación algebraica)
A3{displaystyle A3}	S1⋅ ⋅ 4{displaystyle S1cdot 4}	pieza (por ejemplo, 00L0 — rey blanco)
A4{displaystyle A4}	()A2,A3){displaystyle (A2,A3)}	pieza en un tablero (por ejemplo L00, 00L; 00L0 — rey blanco en e2)
A5{displaystyle A5}	64× × A3{displaystyle 64times A3}	tabla (piezas de piezas, describe qué pieza contiene cada una de 64 plazas)
A10{displaystyle A10}	()A5,S0,S1⋅ ⋅ 4,A2){displaystyle (A5,S0,S1cdot 4,A2)}	estado del juegoA5{displaystyle A5}- bordo, S0{displaystyle S0}- que se mueve, S1⋅ ⋅ 4{displaystyle S1cdot 4}— posibilidad de castling (2 para blanco y 2 para negro), A2 — información sobre la célula en la que se mueve En passant es posible

Identificadores

Los identificadores son caracteres alfanuméricos con un número. Existen los siguientes tipos de identificadores para las variables:

• Valores de entrada (alemán: Eingabewerte, Variablen) - marcado con una carta V.
• Valores intermedios, temporales (alemán: Zwischenwerte) - marcado con una letra Z.
• Constantes (alemán: Constanten) - marcado con una carta С.
• Valores de rendimiento (alemán: Resultatwerte) - marcado con una carta R.

La variable particular de algún tipo se identifica por un número, escrito debajo del tipo. Por ejemplo:

V0{displaystyle {begin{matrix}Vend{matrix}}, Z2{displaystyle {begin{matrix}Z2end{matrix}}, C31{displaystyle {begin{matrix}C31end{matrix}} etc.

Los programas y subprogramas están marcados con una letra P, seguida de un número de programa (y opcionalmente un subprograma). Por ejemplo P13{displaystyle P13}, P5⋅ ⋅ 7{displaystyle P5cdot 7}.

Valor de salida del programa P13{displaystyle P13} guardado allí en variable R0{displaystyle {begin{matrix}Rend{matrix}} está disponible para otros subprogramas bajo el identificador R170{displaystyle {begin{matrix}R17end{matrix}}, y valor de lectura de esa variable también significa ejecutar subprograma relacionado.

Acceso a elementos por índice

Plankalkül permite el acceso a elementos separados de la variable utilizando "índice combinado" (German: Komponenten-Index). Cuando, por ejemplo, el programa recibe entrada en variable V0{displaystyle {begin{matrix}Vend{matrix}} tipo A10{displaystyle A10} (Estado del juego), entonces V00{}}- da estado de la junta, V00⋅ ⋅ i{cdot iend{matrix}}}- pieza en número cuadrado I, y V00⋅ ⋅ i⋅ ⋅ j{cdot icdot jend{matrix}}} Un poco número j de esa pieza.

En los lenguajes de programación modernos, eso se describiría mediante una notación similar a V0[0], V0[0][i], V0[0] [i][j] (aunque para acceder a un solo bit en los lenguajes de programación modernos se suele utilizar una máscara de bits).

Sintaxis bidimensional

Debido a que los índices de las variables se escriben verticalmente, cada instrucción de Plankalkül requiere varias filas para escribirse.

La primera fila contiene el tipo de variable, luego el número de variable marcado con la letra V (alemán: Variablen-Index), luego los índices de los subcomponentes variables marcados con K (alemán: Komponenten-Index), y luego (alemán: Struktur-Index) marcado con S, que describe el tipo de variable. No se requiere escribir, pero Zuse señala que esto ayuda a leer y comprender el programa.

En la línea S{displaystyle S. tipos S0{displaystyle S0} y S1{displaystyle S1} podría acortarse 0{displaystyle 0} y 1{displaystyle 1}.

Ejemplos:

VV3KSm× × 2× × 1⋅ ⋅ n{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}	variable V3 - lista de m{displaystyle m} pares de valores de tipo S1⋅ ⋅ n{displaystyle S1cdot n}
VV3Sm× × 2× × 1⋅ ⋅ n{displaystyle {begin{array}{r habitl} limitadaV\Vcera3S recurmtimes 2times 1cdot nend{array}}	Row K podría ser saltada cuando está vacía. Por lo tanto, esta expresión significa lo mismo que antes.
VV3Ki⋅ ⋅ 0⋅ ⋅ 7S0{displaystyle {begin{array}{r habitl {ccc}}} {cdotcdot 0cdot 7cdot 7cdot}}}	Valor de 8 bits (index 7), de primer par (index 0), de elemento і-th variable V3, tiene tipo booleano (S0{displaystyle S0}).

Los índices pueden ser no solo constantes. Las variables podrían usarse como índices para otras variables, y eso está marcado con una línea, que muestra en qué índice de componente se usaría el valor de la variable:

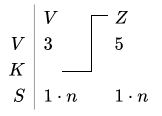Z5-th elemento de variable V3. Equivalente a la expresión V3[Z5] en muchos lenguajes de programación modernos.

Operación de asignación

Zuse presentó en su cálculo un operador de asignación, desconocido en matemáticas ante él. Lo marcó con «⇒ ⇒ {displaystyle "Rightarrow"», y lo llamó cede-sign (alemán: Ergibt-Zeichen). El uso del concepto de asignación es una de las diferencias clave entre matemáticas y informática.

Zuse escribió esa expresión:

Z+1⇒ ⇒ ZV11{displaystyle {begin{array}{r habitlll} reducidaZ+1 ventajaRightarrow "Z\V círculo1 diez"

es análoga a una ecuación matemática más tradicional:

Z+1=ZV11Kii+1{displaystyle {begin{array}{r habitlll} reducidaZ+1 tendrían una relación con el tema de la muerte.

Hay afirmaciones de que Konrad Zuse utilizó inicialmente el glifo como signo de asignación, y comenzó a usar ⇒ ⇒ {displaystyle "Rightarrow" bajo la influencia de Heinz Rutishauser. Knuth y Pardo creen que Zuse siempre escribió ⇒ ⇒ {displaystyle "Rightarrow", y eso fue presentado por los editores de «Über den allgemeinen Plankalkül als Mittel zur Formulierung schematisch-kombinativer Aufgaben» en 1948. En la conferencia ALGOL 58 en Zurich, los participantes europeos se propusieron utilizar para el carácter de asignación presentado por Zuse, pero la delegación estadounidense insistió en :=.

La variable que almacena el resultado de una asignación (valor l) se escribe a la derecha del operador de asignación. La primera asignación a la variable se considera una declaración.

El lado izquierdo del operador de asignación se utiliza para la expresión (alemán: Ausdruck), que define qué valor se asignará a la variable. Las expresiones podrían utilizar operadores aritméticos, operadores booleanos y operadores de comparación (=,ل ل ,≤ ≤ {displaystyle =,neqleq} etc.).

La operación de exponenciación se escribe de manera similar a la operación de indexación, usando líneas en notación 2d:

Flujo de control

Terminología

Zuse llamó a un solo programa un Rechenplan ("plan de computación"). Imaginó lo que llamó un Planfertigungsgerät ("dispositivo de ensamblaje de planes"), que traduciría automáticamente la formulación matemática de un programa en material de película perforada legible por máquina.

Ejemplo

La notación original era bidimensional. Para una implementación posterior en la década de 1990, se desarrolló una notación lineal.

El siguiente ejemplo define una función max3 (en una transcripción lineal) que calcula el máximo de tres variables:

P1 max3 (V0[:8.0],V1[:8.0],V2[:8.0]) → R0[:8.0]
max(V0[:8.0],V1[:8.0]) → Z1[:8.0]
max(Z1[:8.0],V2[:8.0]) → R0[:8.0]
FIN
P2 max (V0[:8.0],V1[:8.0]) → R0[:8.0]
V0[:8.0] → Z1[:8.0]
(Z1[:8.0] ANTE V1[:8.0]) → V1[:8.0] → Z1[:8.0]
Z1[:8.0] → R0[:8.0]
FIN