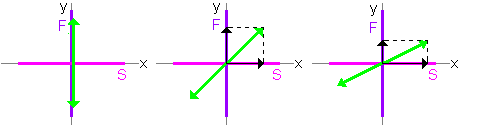
Placa de onda

Campo eléctrico paralelo al eje óptico

Campo eléctrico perpendicular al eje

El campo combinado

La luz polarizada linealmente que entra en una placa de media onda se puede resolver en dos ondas, paralelas y perpendiculares al eje óptico de la onda. En la placa, la onda paralela se propaga ligeramente más lenta que la perpendicular. En el lado lejano de la placa, la onda paralela es exactamente la mitad de una longitud de onda retardada en relación con la onda perpendicular, y la combinación resultante es una imagen de espejo del estado de polarización de entrada (en relación con el eje óptico).

Una placa de ondas o retardador es un dispositivo óptico que altera el estado de polarización de una onda de luz que viaja a través de él. Dos tipos comunes de placas de onda son la placa de media onda, que cambia la dirección de polarización de la luz polarizada linealmente, y la placa de cuarto de onda, que convierte la luz polarizada linealmente en circularmente. luz polarizada y viceversa. También se puede usar una placa de cuarto de onda para producir polarización elíptica.

Las placas onduladas están construidas con un material birrefringente (como cuarzo o mica, o incluso plástico), cuyo índice de refracción es diferente para la luz polarizada linealmente a lo largo de uno u otro de dos ejes de cristal perpendiculares. El comportamiento de una placa ondulada (es decir, si es una placa de media onda, una placa de un cuarto de onda, etc.) depende del espesor del cristal, la longitud de onda de la luz y la variación del índice de refracción. Mediante la elección apropiada de la relación entre estos parámetros, es posible introducir un cambio de fase controlado entre los dos componentes de polarización de una onda de luz, alterando así su polarización.

Un uso común de las placas de onda, en particular las placas de tinte sensible (onda completa) y de cuarto de onda, es en mineralogía óptica. La adición de placas entre los polarizadores de un microscopio petrográfico facilita la identificación óptica de minerales en secciones delgadas de rocas, en particular al permitir la deducción de la forma y orientación de las indicaciones ópticas dentro de las secciones de cristal visible. Esta alineación puede permitir la discriminación entre minerales que de otro modo parecen muy similares en luz polarizada plana y polarizada cruzada.

Principios de funcionamiento

Una onda en un cristal uniaxial se separará en dos componentes, uno paralelo y uno perpendicular al eje óptico, que acumulará fase a diferentes velocidades. Esto se puede utilizar para manipular el estado de polarización de la onda.

Una placa de onda montada en un montaje giratorio

Una placa de ondas funciona cambiando la fase entre dos componentes de polarización perpendicular de la onda de luz. Una placa ondulada típica es simplemente un cristal birrefringente con una orientación y un grosor cuidadosamente elegidos. El cristal se corta en una placa, con la orientación del corte elegida de manera que el eje óptico del cristal sea paralelo a las superficies de la placa. Esto da como resultado dos ejes en el plano de corte: el eje ordinario, con índice de refracción n_o, y el extraordinario eje, con índice de refracción n_e. El eje ordinario es perpendicular al eje óptico. El eje extraordinario es paralelo al eje óptico. Para una onda de luz que normalmente incide sobre la placa, el componente de polarización a lo largo del eje ordinario viaja a través del cristal con una velocidad v_o = c/ n_o, mientras que la componente de polarización a lo largo del eje extraordinario viaja con una velocidad v_e = c /n_e. Esto conduce a una diferencia de fase entre los dos componentes cuando salen del cristal. Cuando n_e < n_o, como en la calcita, el eje extraordinario se llama eje rápido y el eje ordinario se llama eje lento. Para n_e > n_o la situación se invierte.

Dependiendo del grosor del cristal, la luz con componentes de polarización a lo largo de ambos ejes emergerá en un estado de polarización diferente. La placa de ondas se caracteriza por la cantidad de fase relativa, Γ, que imparte a los dos componentes, que está relacionada con la birrefringencia Δn y el espesor L del cristal por la fórmula

.. =2π π Δ Δ nLλ λ 0,{displaystyle Gamma ={frac {2pi ,Delta n,L}{lambda ♪♪

donde λ₀ es la longitud de onda de vacío de la luz.

Las placas de onda en general, así como los polarizadores, pueden describirse mediante el formalismo de matriz de Jones, que utiliza un vector para representar el estado de polarización de la luz y una matriz para representar la transformación lineal de una placa de onda o polarizador.

Aunque la birrefringencia Δn puede variar ligeramente debido a la dispersión, esta es insignificante comparada con la variación en la diferencia de fase según la longitud de onda de la luz debido a la diferencia de trayectoria fija (λ ₀ en el denominador de la ecuación anterior). Por lo tanto, las placas de ondas se fabrican para trabajar en un rango particular de longitudes de onda. La variación de fase se puede minimizar apilando dos placas de ondas que difieren en una cantidad minúscula en espesor espalda con espalda, con el eje lento de uno a lo largo del eje rápido del otro. Con esta configuración, la fase relativa impartida puede ser, para el caso de una placa de cuarto de onda, un cuarto de longitud de onda en lugar de tres cuartos o un cuarto más un número entero. Esto se denomina placa de ondas de orden cero.

Para una sola placa de onda, cambiar la longitud de onda de la luz introduce un error lineal en la fase. La inclinación de la placa de ondas entra a través de un factor de 1/cos θ (donde θ es el ángulo de inclinación) en la longitud de la trayectoria y, por lo tanto, solo cuadráticamente en la fase. Para la polarización extraordinaria, la inclinación también cambia el índice de refracción al ordinario a través de un factor de cos θ, por lo que combinado con la longitud del camino, el cambio de fase para la luz extraordinaria debido a la inclinación es cero.

Un cambio de fase independiente de la polarización de orden cero necesita una placa con un grosor de una longitud de onda. Para la calcita, el índice de refracción cambia en el primer decimal, de modo que una verdadera placa de orden cero es diez veces más gruesa que una longitud de onda. Para el cuarzo y el fluoruro de magnesio, el índice de refracción cambia en el segundo lugar decimal y las placas de orden cero verdadero son comunes para longitudes de onda superiores a 1 μm.

Tipos de platos

Placa de media onda

Una ola que pasa por un plato de media onda

Para un plato de media onda, la relación entre L, Δn, y λ₀ es elegido para que el cambio de fase entre los componentes de polarización sea Dimension = π. Ahora suponga una onda linealmente polarizada con vector de polarización p^ ^ {displaystyle mathbf {hat {p} es un incidente en el cristal. Deja θ denota el ángulo entre p^ ^ {displaystyle mathbf {hat {p} y f^ ^ {displaystyle mathbf {f}, donde f^ ^ {displaystyle mathbf {f} es el vector a lo largo del eje rápido de la onda. Vamos z denota el eje de propagación de la ola. El campo eléctrico de la onda del incidente es

Eei()kz− − ⋅ ⋅ t)=Ep^ ^ ei()kz− − ⋅ ⋅ t)=E()#⁡ ⁡ Silencio Silencio f^ ^ +pecado⁡ ⁡ Silencio Silencio s^ ^ )ei()kz− − ⋅ ⋅ t),{displaystyle mathbf {E} ,mathrm {e} ^{i(kz-omega t)}=E,mathbf {hat {} ,mathrm {e} ^{i(kz-omega t)}=E(cos theta ,mathbf {hat {f} {f} {f} {f}}} {f}}} {f}f}}}} {f}f}}f}}}}}}}}}}}f}f}}}}}}f} {f}f} {f}f}}f}f}f}f}}}}f} {f} +sin theta ,mathbf {hat {s})mathrm {e} ^{i(kz-omega t)}}

Donde s^ ^ {displaystyle mathbf {f}} yace a lo largo del lento eje de la onda. El efecto de la placa de media onda es introducir un cambio de fase e^i.= e^iπ= 1 - entre f y s componentes de la onda, para que al salir del cristal la onda sea ahora dada por

E()#⁡ ⁡ Silencio Silencio f^ ^ − − pecado⁡ ⁡ Silencio Silencio s^ ^ )ei()kz− − ⋅ ⋅ t)=E[#⁡ ⁡ ()− − Silencio Silencio )f^ ^ +pecado⁡ ⁡ ()− − Silencio Silencio )s^ ^ ]ei()kz− − ⋅ ⋅ t).{displaystyle E(cos theta ,mathbf {hat {f} -sin theta ,mathbf {hat {s})mathrm {e} ^{i(kz-omega t)}=E[cos(-theta)mathbf {hat {hat {f} +sin(-theta)mathbf {hat {s}}mathrm} {e} {iegak} {i} {i} {i} {i} {i} {i} {i} {i} {i}i}i} {i}i}i}i}i}i}i}i}i}i}i} {i} {i}i}i}i} {i}i}i}i}i}i}i}i}i}i}i}i}i}ii}i}i}i}i}i}

Si p^ ^ .{displaystyle mathbf {hat {p}} denota el vector de polarización de la onda saliendo de la onda, entonces esta expresión muestra que el ángulo entre p^ ^ .{displaystyle mathbf {hat {p}} y f^ ^ {displaystyle mathbf {f} es − θ. Evidentemente, el efecto de la placa de media onda es reflejar el vector de polarización de la onda a través del plano formado por los vectores f^ ^ {displaystyle mathbf {f} y z^ ^ {displaystyle mathbf {hat {z}. Para la luz polarizada linealmente, esto equivale a decir que el efecto de la placa de media onda es girar el vector de polarización a través de un ángulo 2θ; sin embargo, para la luz polarizada elíptica la placa de media onda también tiene el efecto de invertir la entrega de la luz.

Placa de cuarto de onda

Dos ondas difieren por un turno de cuarta fase para un eje.

Creación de polarización circular utilizando una placa de onda trimestral y un filtro polarizador

Para una placa de cuarto de onda, la relación entre L, Δn y λ₀ se elige de modo que el cambio de fase entre componentes de polarización es Γ = π/2. Supongamos ahora que una onda polarizada linealmente incide sobre el cristal. Esta onda se puede escribir como

()Eff^ ^ +Ess^ ^ )ei()kz− − ⋅ ⋅ t),{displaystyle (E_{f}mathbf {hat {f} {fnMicrosoft}}

donde los ejes f y s son los ejes rápido y lento de la placa de cuarto de onda, respectivamente, la onda se propaga a lo largo de z eje, y E_f y E_s son reales. El efecto de la placa de cuarto de onda es introducir un término de cambio de fase e^iΓ =e^iπ/2 = i entre las componentes f y s de la onda, de modo que al salir del cristal la onda ahora viene dada por

()Eff^ ^ +iEss^ ^ )ei()kz− − ⋅ ⋅ t).{displaystyle (E_{f}mathbf {hat {f} ## IE_{s}mathbf {hat {s})mathrm {e} ^{i(kz-omega t)}.}

La onda ahora está polarizada elípticamente.

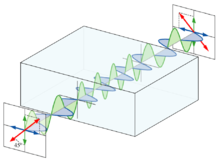
Si el eje de polarización de la onda incidente se elige de modo que forme un ángulo de 45° con los ejes rápido y lento de la placa de onda, entonces E_f = E_s ≡ E, y la onda resultante al salir de la placa de ondas es

E()f^ ^ +is^ ^ )ei()kz− − ⋅ ⋅ t),{displaystyle E(mathbf {f} ##imathbf {hat {s}]mathrm {e} ^{i(kz-omega t)}}}

y la onda está polarizada circularmente.

Si el eje de polarización de la onda incidente se elige de modo que haga un 0° con los ejes rápido o lento de la placa de onda, entonces la polarización no cambiará, por lo que permanecerá lineal. Si el ángulo está entre 0° y 45°, la onda resultante tiene una polarización elíptica.

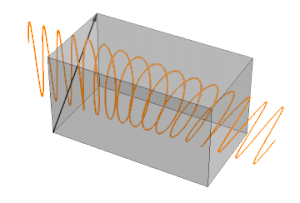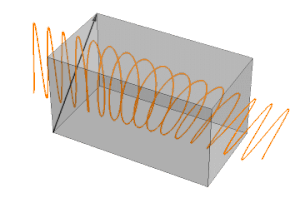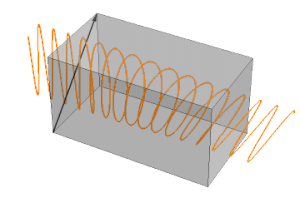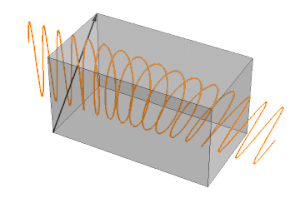
Una polarización circulante se puede visualizar como la suma de dos polarizaciones lineales con una diferencia de fase de 90°. La salida depende de la polarización de la entrada. Suponga que los ejes de polarización x e y son paralelos al eje lento y rápido de la placa de ondas:

La polarización del fotón (o haz) entrante se puede resolver como dos polarizaciones en los ejes x e y. Si la polarización de entrada es paralela al eje rápido o lento, entonces no hay polarización del otro eje, por lo que la polarización de salida es la misma que la de entrada (solo la fase más o menos retrasada). Si la polarización de entrada es de 45° con respecto al eje rápido y lento, la polarización en esos ejes es igual. Pero la fase de la salida del eje lento se retrasará 90° con la salida del eje rápido. Si no se muestra la amplitud sino ambos valores de seno, entonces x e y combinados describirán un círculo. Con otros ángulos que no sean 0° o 45°, los valores en el eje rápido y lento serán diferentes y su salida resultante describirá una elipse.

Placa de onda completa o tintado sensible

Una placa de onda completa introduce una diferencia de fase de exactamente una longitud de onda entre las dos direcciones de polarización, para una longitud de onda de luz. En mineralogía óptica, es común usar una placa de onda completa diseñada para luz verde (una longitud de onda cercana a los 540 nm). La luz blanca polarizada linealmente que pasa a través de la placa se polariza elípticamente, excepto la longitud de onda de la luz verde, que permanecerá lineal. Si se agrega un polarizador lineal orientado perpendicularmente a la polarización original, esta longitud de onda verde se extingue por completo pero quedan elementos de los otros colores. Esto significa que, en estas condiciones, la placa aparecerá con un tono intenso de rojo violeta, a veces conocido como "tinte sensible". Esto da lugar a los nombres alternativos de esta placa, la placa de tinte sensible o (menos comúnmente) placa de tinte rojo. Estas placas se usan ampliamente en mineralogía para ayudar en la identificación de minerales en secciones delgadas de rocas.

Placas de onda de orden múltiple frente a de orden cero

Una placa de ondas de orden múltiple está hecha de un solo cristal birrefringente que produce un múltiplo entero de la retardación nominal (por ejemplo, una placa de media onda de orden múltiple puede tener una retardación absoluta de 37λ/2). Por el contrario, una placa de ondas de orden cero produce exactamente el retardo especificado. Esto se puede lograr combinando dos placas de ondas de orden múltiple de manera que la diferencia en sus retardos produzca el retardo neto (verdadero) de la placa de ondas. Las placas de onda de orden cero son menos sensibles a los cambios de temperatura y longitud de onda, pero son más caras que las de orden múltiple.

Al apilar una serie de placas de onda de diferente orden con filtros de polarización entre ellas se obtiene un filtro de Lyot. Los filtros se pueden rotar o las placas de ondas se pueden reemplazar con capas de cristal líquido para obtener una banda de paso ampliamente sintonizable en el espectro de transmisión óptica.

Uso de placas de ondas en mineralogía y petrología óptica

Las placas de tinte sensible (onda completa) y de cuarto de onda se utilizan ampliamente en el campo de la mineralogía óptica. La adición de placas entre los polarizadores de un microscopio petrográfico facilita la identificación óptica de minerales en secciones delgadas de rocas, en particular al permitir la deducción de la forma y orientación de las indicaciones ópticas dentro de las secciones de cristal visible.

En términos prácticos, la placa se inserta entre los polarizadores perpendiculares en un ángulo de 45 grados. Esto permite llevar a cabo dos procedimientos diferentes para investigar el mineral bajo la mira del microscopio. En primer lugar, en luz polarizada cruzada ordinaria, la placa se puede usar para distinguir la orientación de la indicatriz óptica en relación con el alargamiento del cristal, es decir, si el mineral es de "longitud lenta" o "longitud rápida" – en función de si los colores de interferencia visibles aumentan o disminuyen en un orden cuando se agrega la placa. En segundo lugar, un procedimiento un poco más complejo permite utilizar una placa de tinte junto con técnicas de figura de interferencia para permitir la medición del ángulo óptico del mineral. El ángulo óptico (a menudo anotado como "2V") puede ser un diagnóstico del tipo de mineral y, en algunos casos, revelar información sobre la variación de la composición química dentro de un solo tipo de mineral.