Pi

ImprimirCitar

Número, aproximadamente 3.14

El número $π$ (se despidió como "pi") es una constante matemática que es la relación de la circunferencia de un círculo a su diámetro, aproximadamente igual a 3.14159. El número $π$ aparece en muchas fórmulas a través de las matemáticas y la física. Es un número irracional, lo que significa que no se puede expresar exactamente como una proporción de dos enteros, aunque fracciones tales como ${displaystyle {tfrac {22}{7}}}$ se utilizan comúnmente para aproximarlo. En consecuencia, su representación decimal nunca termina, ni entra en un patrón de repetición permanente. Es un número trascendental, lo que significa que no puede ser una solución de una ecuación que implica sólo sumas, productos, poderes e enteros. La trascendencia de $π$ implica que es imposible resolver el antiguo desafío de cubrir el círculo con una brújula y una recta. Los dígitos decimales $π$ parece ser distribuida aleatoriamente, pero no se ha encontrado ninguna prueba de esta conjetura.

Durante miles de años, los matemáticos han intentado ampliar su comprensión de $π$ , a veces calculando su valor en un alto grado de precisión Las civilizaciones antiguas, incluidos los egipcios y los babilonios, requerían aproximaciones bastante precisas de $π$ para realizar cálculos prácticos. Alrededor del año 250 BC, el matemático griego Arquímedes creó un algoritmo para aproximar $π$ con precisión arbitraria. En el siglo V d. C., los matemáticos chinos aproximaron $π$ a siete dígitos, mientras que los matemáticos indios hicieron una aproximación de cinco dígitos, ambos usando formas geométricas. tecnicas La primera fórmula computacional para $π$ , basada en series infinitas, se descubrió un milenio después. El primer uso conocido de la letra griega π para representar la relación entre la circunferencia de un círculo y su diámetro fue realizado por el matemático galés William Jones en 1706.

La invención del cálculo pronto condujo al cálculo de cientos de dígitos de $π$ , suficientes para todos los cálculos científicos prácticos. Sin embargo, en los siglos XX y XXI, matemáticos e informáticos han buscado nuevos enfoques que, combinados con una potencia computacional cada vez mayor, ampliaron la representación decimal de $π$ a muchos billones de dígitos. Estos cálculos están motivados por el desarrollo de algoritmos eficientes para calcular series numéricas, así como por la búsqueda humana de batir récords. Los extensos cálculos involucrados también se han utilizado para probar supercomputadoras.

Debido a que su definición se relaciona con el círculo, $π$ se encuentra en muchas fórmulas en trigonometría y geometría, especialmente aquellas relacionadas con círculos, elipses y esferas. También se encuentra en fórmulas de otros temas científicos, como cosmología, fractales, termodinámica, mecánica y electromagnetismo. En el análisis matemático moderno, a menudo se define sin ninguna referencia a la geometría; por lo tanto, también aparece en áreas que tienen poco que ver con la geometría, como la teoría de números y la estadística. La ubicuidad de $π$ la convierte en una de las constantes matemáticas más conocidas dentro y fuera de la ciencia. Se han publicado varios libros dedicados a $π$ y cálculos récord de los dígitos de $π$ suelen generar titulares de noticias.

Fundamentos

Nombre

El símbolo utilizado por los matemáticos para representar la relación entre la circunferencia de un círculo y su diámetro es la letra griega minúscula π, a veces escrita como pi. En inglés, $π$ se pronuncia como "pastel" (PY). En el uso matemático, la letra minúscula $π$ se distingue de su contraparte mayúscula y ampliada $Π$ , que denota un producto de una secuencia, de forma análoga a cómo $Σ$ denota una suma.

La elección del símbolo $π$ se analiza en la sección Adopción del símbolo π.

Definición

La circunferencia de un círculo es ligeramente más de tres veces mientras su diámetro. La relación exacta se llama

π

$π$ se define comúnmente como la relación de la circunferencia de un círculo $C$ a su diámetro $d$ :

{displaystyle pi ={frac {C}{d}}}

La relación $C / d$ es constante, independientemente del tamaño del círculo. Por ejemplo, si un círculo tiene el doble de diámetro que otro círculo, también tendrá el doble de circunferencia, conservando la relación $C / d$ . Esta definición de $π$ hace uso implícito de geometría plana (euclidiana); aunque la noción de círculo se puede extender a cualquier geometría curva (no euclidiana), estos nuevos círculos ya no cumplirán la fórmula $π = C / d$ .

Aquí, la circunferencia de un círculo es la longitud del arco alrededor del perímetro del círculo, una cantidad que puede definirse formalmente independientemente de la geometría usando límites, un concepto en cálculo. Por ejemplo, se puede calcular directamente la longitud del arco de la mitad superior del círculo unitario, dada en coordenadas cartesianas por la ecuación $x 2 + y 2 = 1$ , como la integral:

{displaystyle pi =int _{-1}^{1}{frac {dx}{sqrt {1-x^{2}}}}.}

Una integral como esta fue adoptada como la definición de $π$ por Karl Weierstrass, quien la definió directamente como una integral en 1841.

La integración ya no se usa comúnmente en una primera definición analítica porque, como explica Remmert 2012, el cálculo diferencial generalmente precede al cálculo integral en el plan de estudios universitario, por lo que es deseable tener una definición de estilo $π$ que no se basa en este último. Una de esas definiciones, debida a Richard Baltzer y popularizada por Edmund Landau, es la siguiente: $π$ es el doble del número positivo más pequeño en el que la función coseno es igual a 0. $π$ es también el número positivo más pequeño en el que la función seno es igual a cero, y la diferencia entre ceros consecutivos de la función seno. El coseno y el seno se pueden definir independientemente de la geometría como una serie de potencias o como la solución de una ecuación diferencial.

Con un espíritu similar, $π$ se puede definir usando las propiedades de la exponencial compleja, $exp z$ , de una variable compleja $z$ . Al igual que el coseno, el exponencial complejo se puede definir de varias maneras. El conjunto de números complejos en los que $exp z$ es igual a uno es entonces una progresión aritmética (imaginaria) de la forma:

{displaystyle {dots-2pi i,0,2pi i,4pi i,dots }={2pi kimid kin mathbb {Z} }}

y hay un único número real positivo $π$ con esta propiedad.

Una variación de la misma idea, haciendo uso de conceptos matemáticos sofisticados de topología y álgebra, es el siguiente teorema: hay un isomorfismo continuo único (hasta el automorfismo) del grupo R/Z de números reales bajo módulo de suma de enteros (el grupo circular), sobre el grupo multiplicativo de números complejos de valor absoluto uno. El número $π$ se define entonces como la mitad de la magnitud de la derivada de este homomorfismo.

Irracionalidad y normalidad

$π$ es un número irracional, lo que significa que no se puede escribir como la proporción de dos enteros. Fracciones como $22 / 7$ y $355 / 113$ se utilizan comúnmente para aproximado $π$ , pero ninguna fracción común (proporción de números enteros) puede ser su valor exacto. Debido a que $π$ es irracional, tiene un número infinito de dígitos en su representación decimal y no se asienta en un patrón de repetición infinita de dígitos Hay varias pruebas de que π es irracional; generalmente requieren cálculo y se basan en la técnica reductio ad absurdum. El grado en que $π$ se puede aproximar mediante números racionales (llamada medida de irracionalidad) no se conoce con precisión; las estimaciones han establecido que la medida de irracionalidad es mayor que la medida de $e$ o $ln 2$ pero menor que la medida de los números de Liouville.

Los dígitos de $π$ no tienen un patrón aparente y han superado las pruebas de aleatoriedad estadística, incluidas las pruebas de normalidad; un número de longitud infinita se llama normal cuando todas las posibles secuencias de dígitos (de cualquier longitud dada) aparecen con la misma frecuencia. La conjetura de que $π$ es normal no se ha probado ni refutado.

Desde la llegada de las computadoras, una gran cantidad de dígitos de $π$ han estado disponibles para realizar análisis estadísticos. Yasumasa Canadá ha realizado análisis estadísticos detallados sobre los dígitos decimales de $π$ y los encontró consistentes con la normalidad; por ejemplo, las frecuencias de los diez dígitos del 0 al 9 se sometieron a pruebas de significación estadística y no se encontró evidencia de un patrón. Cualquier secuencia aleatoria de dígitos contiene subsecuencias arbitrariamente largas que parecen no aleatorias, según el teorema del mono infinito. Por lo tanto, debido a que la secuencia de $π$ 's dígitos pasa las pruebas estadísticas de aleatoriedad, contiene algunas secuencias de dígitos que pueden aparecen no aleatorias, como una secuencia de seis 9 consecutivos que comienza en el lugar decimal 762 de la representación decimal de $π$ . Esto también se llama el "punto de Feynman" en el folclore matemático, después de Richard Feynman, aunque no se conoce ninguna conexión con Feynman.

Trascendencia

Porque...

π

es un número trascendental, cubrir el círculo no es posible en un número finito de pasos utilizando las herramientas clásicas de la brújula y la rectitud.

Además de ser irracional, $π$ también es un número trascendental, lo que significa que no es la solución de ningún no -ecuación polinomial constante con coeficientes racionales, como $x 5 / 120 - x 3 / 6 + x = 0$ .

La trascendencia de $π$ tiene dos consecuencias importantes: Primero, $π$ no se puede expresar usando ninguna combinación finita de números racionales y raíces cuadradas o raíces enésimas (como $3 \sqrt 31$ o $\sqrt 10). En segundo lugar, dado que ningún número trascendental se puede construir con regla y compás, no es posible "cuadrar el círculo". En otras palabras, es imposible construir, utilizando únicamente compás y regla, un cuadrado cuya área sea exactamente igual al área de un círculo dado. La cuadratura de un círculo fue uno de los problemas de geometría importantes de la antigüedad clásica. Los matemáticos aficionados en los tiempos modernos a veces han intentado cuadrar el círculo y reclamar el éxito, a pesar de que es matemáticamente imposible.$

Fracciones continuas

Como todos los números irracionales, $π$ no se puede representar como una fracción común (también conocida como fracción simple o vulgar), por la definición misma de número irracional (es decir, no un número racional). Pero cada número irracional, incluido $π$ , puede representarse mediante una serie infinita de fracciones anidadas, denominada fracción continua:

{displaystyle pi =3+textstyle {cfrac {1}{7+textstyle {cfrac {1}{15+textstyle {cfrac {1}{1+textstyle {cfrac {1}{292+textstyle {cfrac {1}{1+textstyle {cfrac {1}{1+textstyle {cfrac {1}{1+ddots }}}}}}}}}}}}}}}

Al truncar la fracción continua en cualquier punto se obtiene una aproximación racional para $π$ ; los primeros cuatro son $3$ , $22 / 7$ , $333 / 106$ y $355 / 113$ . Estos números se encuentran entre las aproximaciones históricas más conocidas y más utilizadas de la constante. Cada aproximación generada de esta manera es una mejor aproximación racional; es decir, cada una está más cerca de $π$ que cualquier otra fracción con el mismo denominador o uno más pequeño. Debido a que se sabe que $π$ es trascendental, por definición no es algebraico y, por lo tanto, no puede ser un irracional cuadrático. Por lo tanto, $π$ no puede tener una fracción continua periódica. Aunque la fracción continua simple para $π$ (que se muestra arriba) tampoco muestra ningún otro patrón obvio, los matemáticos han descubierto varias fracciones continuas generalizadas que hacen, tales como:

{displaystyle {begin{aligned}pi &=3+textstyle {cfrac {1^{2}}{6+textstyle {cfrac {3^{2}}{6+textstyle {cfrac {5^{2}}{6+textstyle {cfrac {7^{2}}{6+textstyle {cfrac {9^{2}}{6+ddots }}}}}}}}}}=textstyle {cfrac {4}{1+textstyle {cfrac {1^{2}}{2+textstyle {cfrac {3^{2}}{2+textstyle {cfrac {5^{2}}{2+textstyle {cfrac {7^{2}}{2+ddots }}}}}}}}}}=textstyle {cfrac {4}{1+textstyle {cfrac {1^{2}}{3+textstyle {cfrac {2^{2}}{5+textstyle {cfrac {3^{2}}{7+textstyle {cfrac {4^{2}}{9+ddots }}}}}}}}}}end{aligned}}}

Valor aproximado y dígitos

Algunas aproximaciones de pi incluyen:

Integers: 3
Fracciones: Las fracciones aproximadas incluyen (para aumentar la precisión) 22/7, 333/106, 355/113, 52163/16604, 103993/33102, 104348/33215, y 245850922/78256779. (Lista se selecciona términos de OEIS: A063674 y OEIS: A063673.)
Digits: Los primeros 50 dígitos decimales son 3.14159265358979323846264338327950288419716939937510... (ver OEIS: A000796)

Dígitos en otros sistemas numéricos

Los primeros 48 dígitos binarios (base 2) (llamados bits) son 11.00100100001111110110Graben 19, 10101000100010000101Graben 19, 10100011... (ver OEIS: A004601)
Los primeros 20 dígitos en hexadecimal (base 16) son 3.243F6A8885A308D31319... (ver OEIS: A062964)
Los primeros cinco dígitos sexagesimal (base 60) son 3;8,29,44,0,47 (ver OEIS: A06070707)
Los primeros 38 dígitos en el sistema de numeral ternario son 10.0102110122220102110021111102212222201... (ver OEIS: A004602)

Números complejos y la identidad de Euler

La asociación entre poderes imaginarios del número

e

y puntos en el círculo de unidad centrado en el origen en el plano complejo dado por la fórmula de Euler

Cualquier número complejo, digamos $z$ , puede expresarse usando un par de números reales. En el sistema de coordenadas polares, se usa un número (radio o r) para representar la distancia de $z$ desde el origen del plano complejo, y el otro (ángulo o $φ$ ) el giro en sentido antihorario desde la recta real positiva:

{displaystyle z=rcdot (cos varphi +isin varphi),}

donde $i$ es la unidad imaginaria que satisface $i 2$ = −1. La frecuente aparición de $π$ en análisis complejo puede estar relacionada con el comportamiento de la función exponencial de variable compleja, descrita por Euler&# 39;s fórmula:

{displaystyle e^{ivarphi }=cos varphi +isin varphi}

donde la constante e es la base del logaritmo natural. Esta fórmula establece una correspondencia entre potencias imaginarias de $e$ y puntos de la circunferencia unitaria centrados en el origen del plano complejo. Establecer $φ$ = $π$ en Euler&#39 Su fórmula da como resultado la identidad de Euler, célebre en matemáticas debido a que contiene cinco importantes constantes matemáticas:

{displaystyle e^{ipi }+1=0.}

Hay $n$ diferentes números complejos $z$ que satisfacen $z n = 1$ , y estos se denominan " $n$ -ésimas raíces de unidad" y están dadas por la fórmula:

{displaystyle e^{2pi ik/n}qquad (k=0,1,2,dotsn-1).}

Historia

Antigüedad

Las aproximaciones más conocidas a $π$ que datan antes de la era común tenían una precisión de dos decimales; esto se mejoró en las matemáticas chinas en particular a mediados del primer milenio, con una precisión de siete decimales. Después de esto, no se hicieron más progresos hasta finales del período medieval.

Las primeras aproximaciones escritas de $π$ se encuentran en Babilonia y Egipto, ambas dentro del uno por ciento del valor real. En Babilonia, una tablilla de arcilla fechada entre 1900 y 1600 a. "math" class="sfrac tion">25/8 = 3,125. En Egipto, el Papiro Rhind, fechado alrededor de 1650 a. C. pero copiado de un documento fechado en 1850 a. C., tiene una fórmula para el área de un círculo que trata $π$ como (16/9)² ≈ 3.16. Aunque algunos piramidólogos como Flinders Petrie han teorizado que la Gran Pirámide de Giza se construyó con proporciones relacionadas con $π$ , esta teoría no es ampliamente aceptado por los estudiosos. En los Shulba Sutras de las matemáticas indias, que datan de una tradición oral del primer o segundo milenio antes de Cristo, se dan aproximaciones que se han interpretado de diversas formas como aproximadamente 3,08831, 3,08833, 3,004, 3 o 3,125.

Era de aproximación de polígonos

π

se puede estimar computando los perímetros de polígonos circunscritos e inscritos.

Arquímedes desarrolló el enfoque poligonal de aproximación

π

El primer algoritmo registrado para calcular rigurosamente el valor de $π$ fue un enfoque geométrico usando polígonos, ideado alrededor del año 250 a. matemático griego Arquímedes. Este algoritmo poligonal dominó durante más de 1000 años y, como resultado, $π$ a veces se conoce como la constante de Arquímedes. Arquímedes calculó los límites superior e inferior de $π$ dibujando un hexágono regular dentro y fuera de un círculo, y duplicando sucesivamente el número de lados hasta llegó a un polígono regular de 96 lados. Al calcular los perímetros de estos polígonos, demostró que $223 / 71 < π < 22 / 7$ (es decir $3.1408 < π < 3.1429$ ). Arquímedes' límite superior de $22 / 7$ puede haber llevado a una creencia popular generalizada de que $π$ es igual a $22 / 7$ . Alrededor del año 150 d. C., el científico greco-romano Ptolomeo, en su Almagest, dio un valor para $π$ de 3.1416, que pudo haber obtenido de Arquímedes o de Apolonio de Perge. Los matemáticos que usaban algoritmos poligonales alcanzaron 39 dígitos de $π$ en 1630, un récord que solo se rompió en 1699 cuando se usaron series infinitas para llegar a 71 dígitos.

En la antigua China, los valores de $π$ incluían 3,1547 (alrededor del año 1 d. C.), $\sqrt 10$ (100 d. C., aproximadamente 3,1623), y $142 / 45$ (siglo III, aproximadamente 3.1556). Alrededor del año 265 d. C., el matemático del Reino Wei, Liu Hui, creó un algoritmo iterativo basado en polígonos y lo usó con un polígono de 3072 lados para obtener un valor de $π$ de 3,1416. Más tarde, Liu inventó un método más rápido para calcular $π$ y obtuvo un valor de 3,14 con un polígono de 96 lados, aprovechando el hecho de que las diferencias de área de polígonos sucesivos forman una serie geométrica con un factor de 4. El matemático chino Zu Chongzhi, alrededor del año 480 d. C., calculó que $3.1415926 < π < 3.1415927$ y sugirió las aproximaciones $π \approx 355 / 113$ = 3.14159292035... y $π \approx 22 / 7$ = 3,142857142857..., que denominó Milü (''relación cercana") y Yuelü ("proporción aproximada"), respectivamente, utilizando el algoritmo de Liu Hui aplicado a un polígono de 12 288 lados. Con un valor correcto para sus siete primeros dígitos decimales, este valor siguió siendo la aproximación más precisa de $π$ disponible durante los siguientes 800 años.

El astrónomo indio Aryabhata utilizó un valor de 3,1416 en su Āryabhaṭīya (499 d. C.). Fibonacci en c. 1220 calculó 3,1418 usando un método poligonal, independiente de Arquímedes. El autor italiano Dante aparentemente empleó el valor $3+ \sqrt 2 / 10 \approx 3,14142$ .

El astrónomo persa Jamshīd al-Kāshī produjo 9 dígitos sexagesimales, aproximadamente el equivalente a 16 dígitos decimales, en 1424 utilizando un polígono de 3 × 2²⁸ lados, que se situó como el récord mundial de aproximadamente 180 años El matemático francés François Viète en 1579 logró 9 dígitos con un polígono de 3×2¹⁷ lados. El matemático flamenco Adriaan van Roomen llegó a 15 decimales en 1593. En 1596, el matemático holandés Ludolph van Ceulen alcanzó los 20 dígitos, un récord que luego aumentó a 35 dígitos (como resultado, $π$ fue llamado el "número ludolfo" en Alemania hasta principios del siglo XX). El científico holandés Willebrord Snellius alcanzó los 34 dígitos en 1621, y el astrónomo austríaco Christoph Grienberger llegó a los 38 dígitos en 1630 usando 10⁴⁰ lados. Christiaan Huygens pudo llegar a 10 decimales en 1654 utilizando un método ligeramente diferente equivalente a la extrapolación de Richardson.

Serie infinita

Comparación de la convergencia de varias series históricas infinitas para

π

. S_n es la aproximación después de tomar n términos. Cada subplot posterior magnifica el área sombreada horizontalmente por 10 veces. (haga clic para el detalle)

El cálculo de $π$ fue revolucionado por el desarrollo de técnicas de series infinitas en los siglos XVI y XVII. Una serie infinita es la suma de los términos de una sucesión infinita. Las series infinitas permitieron a los matemáticos calcular $π$ con mucha mayor precisión que Arquímedes y otros que usaban técnicas geométricas. Aunque las series infinitas fueron explotadas para $π$ más notablemente por matemáticos europeos como James Gregory y Gottfried Wilhelm Leibniz, el enfoque también apareció en el Escuela de Kerala en algún momento entre 1400 y 1500 d.C. Alrededor del año 1500 d. C., se presentó una descripción escrita de una serie infinita que podría usarse para calcular $π$ en verso sánscrito en Tantrasamgraha de Nilakantha Somayaji. La serie se presenta sin pruebas, pero las pruebas se presentan en un trabajo posterior, Yuktibhāṣā, de alrededor de 1530 d.C. Nilakantha atribuye la serie a un matemático indio anterior, Madhava de Sangamagrama, que vivió c. 1350 - c. 1425. Se describen varias series infinitas, incluidas series para seno, tangente y coseno, que ahora se denominan serie de Madhava o serie de Gregory-Leibniz. Madhava usó series infinitas para estimar $π$ en 11 dígitos alrededor de 1400, pero ese valor fue mejorado alrededor de 1430 por el matemático persa Jamshīd al. -Kāshī, utilizando un algoritmo poligonal.

En 1593, François Viète publicó lo que ahora se conoce como la fórmula de Viète, un producto infinito (en lugar de una suma infinita, que se usa más típicamente en $π$ cálculos):

{displaystyle {frac {2}{pi }}={frac {sqrt {2}}{2}}cdot {frac {sqrt {2+{sqrt {2}}}}{2}}cdot {frac {sqrt {2+{sqrt {2+{sqrt {2}}}}}}{2}}cdots }

En 1655, John Wallis publicó lo que ahora se conoce como producto de Wallis, también un producto infinito:

{displaystyle {frac {pi }{2}}={Big (}{frac {2}{1}}cdot {frac {2}{3}}{Big)}cdot {Big (}{frac {4}{3}}cdot {frac {4}{5}}{Big)}cdot {Big (}{frac {6}{5}}cdot {frac {6}{7}}{Big)}cdot {Big (}{frac {8}{7}}cdot {frac {8}{9}}{Big)}cdots }

A formal portrait of a man, with long hair

Isaac Newton utilizó series infinitas para calcular

π

a 15 dígitos, más tarde escribiendo "Me avergüenza decirles cuántas figuras he llevado estos cálculos".

En la década de 1660, el científico inglés Isaac Newton y el matemático alemán Gottfried Wilhelm Leibniz descubrieron el cálculo, lo que condujo al desarrollo de muchas series infinitas para aproximar $π$ . El mismo Newton usó una serie arcsen para calcular una aproximación de 15 dígitos de $π$ en 1665 o 1666, escribiendo "Soy avergonzado de decirle a cuántas cifras llevé estos cálculos, no teniendo otros asuntos en ese momento."

En 1671, James Gregory, e independientemente Leibniz en 1674, publicaron la serie:

{displaystyle arctan z=z-{frac {z^{3}}{3}}+{frac {z^{5}}{5}}-{frac {z^{7}}{7}}+cdots }

Esta serie, a veces llamada serie Gregory-Leibniz, es igual a $π/4$ cuando se evalúa con $z = 1.$

En 1699, el matemático inglés Abraham Sharp utilizó la serie Gregory-Leibniz para ${textstyle z={frac {1}{sqrt {3}}}}$ para calcular $π$ a 71 dígitos, rompiendo el registro anterior de 39 dígitos, que se estableció con un algoritmo poligonal. La serie Gregory-Leibniz para $z=1$ es simple, pero converge muy lentamente (es decir, se acerca la respuesta gradualmente), por lo que no se utiliza en moderno $π$ cálculos.

En 1706, John Machin utilizó la serie de Gregory-Leibniz para producir un algoritmo que convergía mucho más rápido:

{displaystyle {frac {pi }{4}}=4arctan {frac {1}{5}}-arctan {frac {1}{239}}.}

Machin alcanzó los 100 dígitos de $π$ con esta fórmula. Otros matemáticos crearon variantes, ahora conocidas como fórmulas tipo Machin, que se usaron para establecer varios registros sucesivos para calcular dígitos de $π$ . Las fórmulas tipo máquina siguieron siendo el método más conocido para calcular $π$ hasta bien entrada la era de las computadoras, y se usaron para establecer récords de 250 años, culminando en una aproximación de 620 dígitos en 1946 por Daniel Ferguson, la mejor aproximación lograda sin la ayuda de un dispositivo de cálculo.

En 1844, Zacharias Dase estableció un récord, quien empleó una fórmula similar a Machin para calcular 200 decimales de $π$ en su cabeza a instancias del matemático alemán Carl Friedrich Gauss.

En 1853, el matemático británico William Shanks calculó $π$ en 607 dígitos, pero cometió un error en el dígito 528, representando todo dígitos posteriores incorrectos. Aunque calculó 100 dígitos adicionales en 1873, elevando el total a 707, su error anterior también hizo que todos los dígitos nuevos fueran incorrectos.

Tasa de convergencia

Algunas series infinitas para $π$ convergen más rápido que otras. Dada la elección de dos series infinitas para $π$ , los matemáticos generalmente usarán la que converge más rápidamente porque la convergencia más rápida reduce la cantidad de cálculo necesario para calcular $π$ con cualquier precisión determinada. Una serie infinita simple para $π$ es la serie de Gregory-Leibniz:

{displaystyle pi ={frac {4}{1}}-{frac {4}{3}}+{frac {4}{5}}-{frac {4}{7}}+{frac {4}{9}}-{frac {4}{11}}+{frac {4}{13}}-cdots }

A medida que los términos individuales de esta serie infinita se suman a la suma, el total se acerca gradualmente a $π$ , y con una cantidad suficiente de términos: puede acercarse tanto a $π$ como desee. Sin embargo, converge con bastante lentitud: después de 500 000 términos, produce solo cinco dígitos decimales correctos de $π$ .

Una serie infinita para $π$ (publicada por Nilakantha en el siglo XV) que converge más rápidamente que la serie de Gregory-Leibniz es:

{displaystyle pi =3+{frac {4}{2times 3times 4}}-{frac {4}{4times 5times 6}}+{frac {4}{6times 7times 8}}-{frac {4}{8times 9times 10}}+cdots }

La siguiente tabla compara las tasas de convergencia de estas dos series:

Serie infinita para $π$	Después del primer mandato	Después del segundo mandato	Después del tercer mandato	Después del cuarto período	Después del quinto período	Converges to:
${displaystyle pi ={frac {4}{1}}-{frac {4}{3}}+{frac {4}{5}}-{frac {4}{7}}+{frac {4}{9}}-{frac {4}{11}}+{frac {4}{13}}+cdots }$	4.0000	2.6666...	3.4666...	2.8952...	3.3396...	$π$ = 3.1415...
${displaystyle pi ={3}+{frac {4}{2times 3times 4}}-{frac {4}{4times 5times 6}}+{frac {4}{6times 7times 8}}-cdots }$	3.0000	3.1666...	3.1333...	3.1452...	3.1396...	$π$ = 3.1415...

Después de cinco términos, la suma de la serie Gregory–Leibniz está dentro de 0,2 del valor correcto de $π$ , mientras que la la suma de la serie de Nilakantha está dentro de 0,002 del valor correcto. La serie de Nilakantha converge más rápido y es más útil para calcular dígitos de $π$ . Las series que convergen aún más rápido incluyen la serie de Machin y la serie de Chudnovsky, la última produce 14 dígitos decimales correctos por término.

Irracionalidad y trascendencia

No todos los avances matemáticos relacionados con $π$ tenían como objetivo aumentar la precisión de las aproximaciones. Cuando Euler resolvió el problema de Basilea en 1735, encontrando el valor exacto de la suma de los cuadrados recíprocos, estableció una conexión entre $π$ y los números primos que más tarde contribuyeron al desarrollo y estudio de la función zeta de Riemann:

{displaystyle {frac {pi ^{2}}{6}}={frac {1}{1^{2}}}+{frac {1}{2^{2}}}+{frac {1}{3^{2}}}+{frac {1}{4^{2}}}+cdots }

El científico suizo Johann Heinrich Lambert demostró en 1768 que $π$ es irracional, lo que significa que no es igual al cociente de dos números enteros La prueba de Lambert aprovechó una representación de fracción continua de la función tangente. El matemático francés Adrien-Marie Legendre demostró en 1794 que $π$ ² también es irracional. En 1882, el matemático alemán Ferdinand von Lindemann demostró que $π$ es trascendental, confirmando una conjetura hecha tanto por Legendre como por Euler. Hardy y Wright afirman que "las pruebas fueron posteriormente modificadas y simplificadas por Hilbert, Hurwitz y otros escritores".

Adopción del símbolo π

El primer uso conocido de la letra griega π para representar la relación de la circunferencia de un círculo a su diámetro fue por el matemático galés William Jones en 1706

Leonhard Euler popularizó el uso de la letra griega π en obras que publicó en 1736 y 1748.

En los primeros usos, la letra griega π se utilizó para denotar el semiperímetro (semiperiferia en latín) de un círculo. y se combinó en ratios con δ (para diámetro o semidiametro) o ρ (para radio) para formar constantes del círculo. (Antes de entonces, los matemáticos a veces utilizan letras como c o p en su lugar.) El primer uso grabado es de Oughtred " ${displaystyle delta.pi }$ ", para expresar la relación de periferia y diámetro en las ediciones 1647 y posteriores Clavis Mathematicae. Barrow también usó " ${textstyle {frac {pi }{delta }}}$ "para representar a la constante 3.14... mientras que Gregory usó " ${textstyle {frac {pi }{rho }}}$ "para representar 6.28...

El primer uso conocido de la letra griega $π$ sola para representar la relación entre la circunferencia de un círculo y su diámetro fue del matemático galés William Jones en su obra de 1706 Synopsis Palmariorum Matheseos; o, una Nueva Introducción a las Matemáticas. La letra griega aparece por primera vez allí en la frase "1/2 periferia ( $π$ )" en la discusión de un círculo con radio uno. Sin embargo, escribe que sus ecuaciones para $π$ son de la "pluma lista del verdaderamente ingenioso Sr. John Machin&# 34;, lo que lleva a la especulación de que Machin pudo haber empleado la letra griega antes que Jones. Jones' La notación no fue adoptada de inmediato por otros matemáticos, y la notación de fracciones todavía se usaba hasta 1767.

Euler comenzó a usar la forma de una sola letra a partir de su Ensayo que explica las propiedades del aire de 1727, aunque usó $π$ = 6,28..., la relación entre la periferia y el radio, en este escrito y en algunos posteriores. Euler utilizó por primera vez $π$ = 3.14... en su obra de 1736 Mechanica, y continuó en su muy leído trabajo de 1748 Introductio in analysin infinitorum (escribió: "en aras de la brevedad, escribiremos este número como $π$ ; por lo tanto, $π$ es igual a la mitad de la circunferencia de un círculo de radio 1"). Debido a que Euler mantuvo mucha correspondencia con otros matemáticos en Europa, el uso de la letra griega se extendió rápidamente y la práctica fue adoptada universalmente a partir de entonces en el mundo occidental, aunque la definición todavía variaba entre 3.14... y 6.28... hasta 1761..

Búsqueda moderna de más dígitos

Era informática y algoritmos iterativos

El algoritmo iterativo Gauss–Legendre:
Inicializar
${displaystyle textstyle a_{0}=1,quad b_{0}={frac {1}{sqrt {2}}},quad t_{0}={frac {1}{4}},quad p_{0}=1.}$ Iterate ${displaystyle textstyle a_{n+1}={frac {a_{n}+b_{n}}{2}},quad quad b_{n+1}={sqrt {a_{n}b_{n}}},}$ ${displaystyle textstyle t_{n+1}=t_{n}-p_{n}(a_{n}-a_{n+1})^{2},quad quad p_{n+1}=2p_{n}.}$ Entonces una estimación para $π$ es dado por ${displaystyle textstyle pi approx {frac {(a_{n}+b_{n})^{2}}{4t_{n}}}.}$

El desarrollo de las computadoras a mediados del siglo XX volvió a revolucionar la búsqueda de dígitos de $π$ . Los matemáticos John Wrench y Levi Smith alcanzaron los 1120 dígitos en 1949 usando una calculadora de escritorio. Usando una serie infinita de tangente inversa (arctan), un equipo dirigido por George Reitwiesner y John von Neumann ese mismo año logró 2.037 dígitos con un cálculo que tomó 70 horas de tiempo de computadora en la computadora ENIAC. El récord, siempre basado en una serie arctan, se batió repetidamente (7.480 dígitos en 1957; 10.000 dígitos en 1958; 100.000 dígitos en 1961) hasta alcanzar el millón de dígitos en 1973.

Dos desarrollos adicionales alrededor de 1980 aceleraron una vez más la capacidad de calcular $π$ . Primero, el descubrimiento de nuevos algoritmos iterativos para calcular $π$ , que eran mucho más rápidos que las series infinitas; y segundo, la invención de algoritmos de multiplicación rápida que podían multiplicar grandes números muy rápidamente. Dichos algoritmos son particularmente importantes en los cálculos modernos de $π$ porque la mayor parte del tiempo de la computadora se dedica a la multiplicación. Incluyen el algoritmo de Karatsuba, la multiplicación de Toom-Cook y los métodos basados en la transformada de Fourier.

Los algoritmos iterativos fueron publicados de forma independiente entre 1975 y 1976 por el físico Eugene Salamin y el científico Richard Brent. Estos evitan la dependencia de series infinitas. Un algoritmo iterativo repite un cálculo específico, cada iteración utiliza los resultados de los pasos anteriores como sus entradas y produce un resultado en cada paso que converge al valor deseado. En realidad, el enfoque fue inventado más de 160 años antes por Carl Friedrich Gauss, en lo que ahora se denomina método de la media aritmética-geométrica (método AGM) o algoritmo de Gauss-Legendre. Modificado por Salamin y Brent, también se lo conoce como el algoritmo Brent-Salamin.

Los algoritmos iterativos se utilizaron ampliamente después de 1980 porque son más rápidos que los algoritmos de series infinitas: mientras que las series infinitas suelen aumentar el número de dígitos correctos de forma aditiva en términos sucesivos, los algoritmos iterativos generalmente multiplican el número de dígitos correctos. dígitos en cada paso. Por ejemplo, el algoritmo de Brent-Salamin duplica el número de dígitos en cada iteración. En 1984, los hermanos John y Peter Borwein produjeron un algoritmo iterativo que cuadruplica el número de dígitos en cada paso; y en 1987, uno que aumenta cinco veces el número de dígitos en cada paso. El matemático japonés Yasumasa Kanada utilizó métodos iterativos para establecer varios récords en la computación $π$ entre 1995 y 2002. Esta rápida convergencia llega en un precio: los algoritmos iterativos requieren significativamente más memoria que las series infinitas.

Motivos para calcular π

Como los matemáticos descubrieron nuevos algoritmos, y las computadoras se pusieron a disposición, el número de dígitos decimales conocidos de

π

aumentó dramáticamente. La escala vertical es logarítmica.

Para la mayoría de los cálculos numéricos que involucran $π$ , unos pocos dígitos brindan suficiente precisión. Según Jörg Arndt y Christoph Haenel, treinta y nueve dígitos son suficientes para realizar la mayoría de los cálculos cosmológicos, porque esa es la precisión necesaria para calcular la circunferencia del universo observable con una precisión de un átomo. Teniendo en cuenta los dígitos adicionales necesarios para compensar los errores de redondeo computacional, Arndt concluye que unos pocos cientos de dígitos serían suficientes para cualquier aplicación científica. A pesar de esto, la gente ha trabajado arduamente para calcular $π$ hasta miles y millones de dígitos. Este esfuerzo puede atribuirse en parte a la compulsión humana por batir récords, y tales logros con $π$ a menudo aparecen en los titulares de todo el mundo. También tienen beneficios prácticos, como probar supercomputadoras, probar algoritmos de análisis numérico (incluidos algoritmos de multiplicación de alta precisión); y dentro de las propias matemáticas puras, proporcionando datos para evaluar la aleatoriedad de los dígitos de $π$ .

Serie rápidamente convergente

Srinivasa Ramanujan, trabajando en aislamiento en la India, produjo muchas series innovadoras para computar

π

Las calculadoras $π$ modernas no utilizan algoritmos iterativos exclusivamente. En las décadas de 1980 y 1990 se descubrieron nuevas series infinitas que son tan rápidas como los algoritmos iterativos, pero son más simples y consumen menos memoria. Los algoritmos iterativos rápidos se anticiparon en 1914, cuando el matemático indio Srinivasa Ramanujan publicó docenas de fórmulas nuevas e innovadoras para $π$ , notables por su elegancia, profundidad matemática y convergencia rápida. Una de sus fórmulas, basada en ecuaciones modulares, es

{displaystyle {frac {1}{pi }}={frac {2{sqrt {2}}}{9801}}sum _{k=0}^{infty }{frac {(4k)!(1103+26390k)}{k!^{4}left(396^{4k}right)}}.}

Esta serie converge mucho más rápidamente que la mayoría de las series arctan, incluida la fórmula de Machin. Bill Gosper fue el primero en utilizarlo para avances en el cálculo de $π$ , estableciendo un récord de 17 millones de dígitos en 1985. Ramanujan& Las fórmulas de #39 anticiparon los algoritmos modernos desarrollados por los hermanos Borwein (Jonathan y Peter) y los hermanos Chudnovsky. La fórmula de Chudnovsky desarrollada en 1987 es

{displaystyle {frac {1}{pi }}={frac {sqrt {10005}}{4270934400}}sum _{k=0}^{infty }{frac {(6k)!(13591409+545140134k)}{(3k)!,k!^{3}(-640320)^{3k}}}.}

Genera alrededor de 14 dígitos de $π$ por término y se ha utilizado para establecer varios récords $π$ cálculos, incluido el primero en superar los mil millones (10⁹) dígitos en 1989 por los hermanos Chudnovsky, 10 billones (10¹³) dígitos en 2011 por Alexander Yee y Shigeru Kondo, y 100 billones de dígitos por Emma Haruka Iwao en 2022. Para fórmulas similares, consulte también la serie Ramanujan-Sato.

En 2006, el matemático Simon Plouffe utilizó el algoritmo de relación de enteros PSLQ para generar varias fórmulas nuevas para $π$ , conforme a lo siguiente modelo:

{displaystyle pi ^{k}=sum _{n=1}^{infty }{frac {1}{n^{k}}}left({frac {a}{q^{n}-1}}+{frac {b}{q^{2n}-1}}+{frac {c}{q^{4n}-1}}right),}

donde $q$ es $eπ$ (la constante de Gelfond), $k$ es un número impar, y $a, b, c$ son ciertos números racionales que calculó Plouffe.

Métodos de Montecarlo

La aguja de Buffon. Agujas a y b han caído al azar.

Los puntos aleatorios se colocan en un cuadrado y un círculo inscrito dentro.

Los métodos de Monte Carlo, que evalúan los resultados de múltiples ensayos aleatorios, se pueden usar para crear aproximaciones de $π$ . La aguja de Buffon es una de esas técnicas: si se deja caer una aguja de longitud $ℓ$ $n$ veces sobre una superficie en la que se dibujan líneas paralelas $t$ unidades separadas, y si $x$ de esas veces se detiene cruzando una línea ( $x$ > 0), luego uno puede aproximar $π$ en función de los recuentos:

{displaystyle pi approx {frac {2nell }{xt}}.}

Otro método de Monte Carlo para calcular $π$ es dibujar un círculo inscrito en un cuadrado y colocar puntos al azar en el cuadrado. La relación entre los puntos dentro del círculo y el número total de puntos será aproximadamente igual a $π/4$ .

Cinco paseos aleatorios con 200 pasos. El medio de la muestra

Silencio W 200 Silencio

μ = 56/5

, y así

2(200)μ -2 Entendido 3.19

está dentro

0,05

π

Otra forma de calcular $π$ usando la probabilidad es comenzar con un paseo aleatorio, generado por una secuencia de monedas (justas) lanzamientos: variables aleatorias independientes $X k$ tales que $X k \in {-1,1}$ con probabilidades iguales. El paseo aleatorio asociado es

{displaystyle W_{n}=sum _{k=1}^{n}X_{k}}

para que, para cada $n$ , $W n$ se extrae de una distribución binomial desplazada y escalada. Como $n$ varía, $W n$ define un proceso estocástico (discreto). Entonces $π$ se puede calcular mediante

{displaystyle pi =lim _{nto infty }{frac {2n}{E[|W_{n}|]^{2}}}.}

Este método de Monte Carlo es independiente de cualquier relación con los círculos y es una consecuencia del teorema del límite central, que se analiza a continuación.

Estos métodos de Monte Carlo para aproximar $π$ son muy lentos en comparación con otros métodos y no brindan ninguna información sobre el número de dígitos que se obtienen. Por lo tanto, nunca se usan para aproximar $π$ cuando se desea velocidad o precisión.

Algoritmos de grifo

En 1995 se descubrieron dos algoritmos que abrieron nuevas vías de investigación en $π$ . Se llaman algoritmos de grifo porque, como el agua que gotea de un grifo, producen dígitos únicos de $π$ que no se reutilizan después de que se calculado. Esto contrasta con las series infinitas o los algoritmos iterativos, que retienen y usan todos los dígitos intermedios hasta que se produce el resultado final.

Los matemáticos Stan Wagon y Stanley Rabinowitz produjeron un algoritmo spigot simple en 1995. Su velocidad es comparable a la de los algoritmos arctan, pero no tan rápida como la de los algoritmos iterativos.

Otro algoritmo spigot, el algoritmo de extracción de dígitos BBP, fue descubierto en 1995 por Simon Plouffe:

{displaystyle pi =sum _{k=0}^{infty }{frac {1}{16^{k}}}left({frac {4}{8k+1}}-{frac {2}{8k+4}}-{frac {1}{8k+5}}-{frac {1}{8k+6}}right).}

Esta fórmula, a diferencia de otras anteriores, puede producir cualquier dígito hexadecimal individual de $π$ sin calcular todos los dígitos anteriores. Los dígitos binarios individuales se pueden extraer de dígitos hexadecimales individuales, y los dígitos octales se pueden extraer de uno o dos dígitos hexadecimales. Se han descubierto variaciones del algoritmo, pero aún no se ha encontrado ningún algoritmo de extracción de dígitos que produzca rápidamente dígitos decimales. Una aplicación importante de los algoritmos de extracción de dígitos es validar nuevos reclamos de registros $π$ cálculos: después de reclamar un nuevo registro, el resultado decimal se convierte a hexadecimal y luego se usa un algoritmo de extracción de dígitos para calcular varios dígitos hexadecimales aleatorios cerca del final; si coinciden, esto proporciona una medida de confianza de que todo el cálculo es correcto.

Entre 1998 y 2000, el proyecto de computación distribuida PiHex usó la fórmula de Bellard (una modificación del algoritmo BBP) para calcular el cuadrillonésimo (10¹⁵ésimo) bit de $π$ , que resultó ser 0. En septiembre de 2010, Yahoo! empleado usó la aplicación Hadoop de la empresa en mil computadoras durante un período de 23 días para calcular 256 bits de $π$ en el dos milmillonésimo (2×10¹⁵ésimo) bit, que también resulta ser cero.

Papel y caracterizaciones en matemáticas

Debido a que $π$ está estrechamente relacionado con el círculo, se encuentra en muchas fórmulas de los campos de la geometría y la trigonometría, particularmente las relativas a círculos, esferas o elipses. Otras ramas de la ciencia, como la estadística, la física, el análisis de Fourier y la teoría de números, también incluyen $π$ en algunas de sus fórmulas importantes..

Geometría y trigonometría

El área del círculo es igual

π

veces la zona sombreada. El área del círculo de unidad es

π

$π$ aparece en fórmulas para áreas y volúmenes de formas geométricas basadas en círculos, como elipses, esferas, conos y toros A continuación se encuentran algunas de las fórmulas más comunes que involucran $π$ .

La circunferencia de un círculo con radio $r$ es $2π r$ .
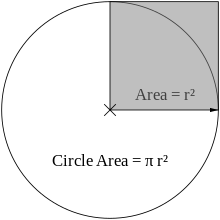
El área de un círculo con radio $r$ es $π r 2$ .
El área de un elipse con eje semi-major $a$ y eje semi-minor $b$ es $π ab$ .
El volumen de una esfera con radio $r$ es $4 / 3 π r 3$ .
La superficie de una esfera con radio $r$ es $4π r 2$ .

Algunas de las fórmulas anteriores son casos especiales del volumen de la bola n-dimensional y el área de superficie de su límite, la esfera (n−1)-dimensional, que se muestra a continuación.

Además de los círculos, existen otras curvas de ancho constante. Por el teorema de Barbier, toda curva de ancho constante tiene un perímetro $π$ multiplicado por su ancho. El triángulo de Reuleaux (formado por la intersección de tres círculos con los lados de un triángulo equilátero como sus radios) tiene el área más pequeña posible para su ancho y el círculo el más grande. También existen curvas no circulares suaves e incluso algebraicas de ancho constante.

Las integrales definidas que describen la circunferencia, el área o el volumen de formas generadas por círculos suelen tener valores que implican $π$ . Por ejemplo, una integral que especifica la mitad del área de un círculo de radio uno está dada por:

{displaystyle int _{-1}^{1}{sqrt {1-x^{2}}},dx={frac {pi }{2}}.}

En esa parte integral de la función $\sqrt 1 - x 2$ representa la altura sobre la $x$ -eje de un semicírculo (la raíz cuadrada es una consecuencia del teorema pitagórico), y la parte integral compone el área debajo del semicírculo.

Unidades de ángulo

Funciones sine y cosina repiten con el período 2

π

Las funciones trigonométricas se basan en ángulos y los matemáticos generalmente usan radianes como unidades de medida. $π$ juega un papel importante en los ángulos medidos en radianes, que se definen de modo que un círculo completo abarque un ángulo de 2 $π$ radianes. La medida del ángulo de 180° es igual a $π$ radianes, y 1° = $π$ /180 radianes.

Las funciones trigonométricas comunes tienen períodos que son múltiplos de $π$ ; por ejemplo, el seno y el coseno tienen el período 2 $π$ , por lo que para cualquier ángulo $θ$ y cualquier número entero $k$ ,

{displaystyle sin theta =sin left(theta +2pi kright){text{ and }}cos theta =cos left(theta +2pi kright).}

Valores propios

Las matices de una cuerda vibradora son las funciones eigenias de la segunda derivada, y forman una progresión armónica. Los eigenvalues asociados forman la progresión aritmética de múltiples enteros

π

Muchas de las apariciones de $π$ en las fórmulas de las matemáticas y las ciencias tienen que ver con su estrecha relación con la geometría. Sin embargo, $π$ también aparece en muchas situaciones naturales que aparentemente no tienen nada que ver con la geometría.

En muchas aplicaciones, desempeña un papel distinguido como un eigenvalue. Por ejemplo, una cadena vibradora idealizada se puede modelar como el gráfico de una función $f$ en el intervalo de unidad $[0, 1]$ , con extremos fijos $f (0) f (1) = 0$ . Los modos de vibración de la cuerda son soluciones de la ecuación diferencial ${displaystyle f''(x)+lambda f(x)=0}$ , o ${displaystyle f''(t)=-lambda f(x)}$ . Así $λ$ es un eigenvalue del segundo operador derivado ${displaystyle fmapsto f''}$ , y está limitado por la teoría de Sturm-Liouville para tomar sólo ciertos valores específicos. Debe ser positivo, ya que el operador es negativo definido, por lo que es conveniente escribir $λ = . 2$ , donde $. ■ 0$ se llama número de onda. Entonces... $f () x) = pecado(π x)$ satisfice las condiciones del límite y la ecuación diferencial con $. = π$ .

El valor $π$ es, de hecho, el mínimo tal valor del número de onda, y se asocia con el modo fundamental de vibración de la cuerda. Una manera de mostrar esto es estimando la energía, que satisface la desigualdad de Wirtinger: para una función ${displaystyle f:[0,1]to mathbb {C} }$ con $f (0) f (1) = 0$ y $f$ , $f'$ ambos cuadrados integrados, tenemos:

{displaystyle pi ^{2}int _{0}^{1}|f(x)|^{2},dxleq int _{0}^{1}|f'(x)|^{2},dx,}

con igualdad precisamente cuando $f$ es un múltiple de $pecado(π) x)$ . Aquí. $π$ aparece como una constante óptima en la desigualdad de Wirtinger, y sigue que es el número de onda más pequeño, utilizando la caracterización de variación del valor eigenvalue. En consecuencia, $π$ es el valor singular más pequeño del operador derivado en el espacio de funciones en $[0, 1]$ desaparecer en ambos extremos (el espacio Sobolev ${displaystyle H_{0}^{1}[0,1]}$ ).

Desigualdades

La antigua ciudad de Carthage fue la solución a un problema isoperimétrico, según una leyenda relatada por el Señor Kelvin: aquellas tierras que bordean el mar que la reina Dido podía encerrar en todos los otros lados dentro de un solo oxhido dado, cortadas en rayas.

El número al que sirve $π$ aparece en problemas similares de valores propios en análisis de dimensiones superiores. Como se mencionó anteriormente, se puede caracterizar por su papel como la mejor constante en la desigualdad isoperimétrica: el área $A$ encerrada por un plano La curva de Jordan del perímetro $P$ satisface la desigualdad

{displaystyle 4pi Aleq P^{2},}

y la igualdad se logra claramente para el círculo, ya que en ese caso $A = π r 2$ y $P = 2π r$ .

En última instancia, como consecuencia de la desigualdad isoperimétrica, $π$ aparece en la constante óptima para la desigualdad crítica de Sobolev en n dimensiones, lo que caracteriza el papel de $π$ también en muchos fenómenos físicos, por ejemplo, los de la clásica teoría potencial. En dos dimensiones, la desigualdad crítica de Sobolev es

{displaystyle 2pi |f|_{2}leq |nabla f|_{1}}

para f una función suave con soporte compacto $R 2$ , $nabla f$ es el gradiente de f, y ${displaystyle |f|_{2}}$ y ${displaystyle |nabla f|_{1}}$ se refieren respectivamente a la L2 y L1-norm. La desigualdad Sobolev es equivalente a la desigualdad isoperimétrica (en cualquier dimensión), con las mismas mejores constantes.

La desigualdad de Wirtinger también se generaliza a las desigualdades de Poincaré de dimensiones superiores que proporcionan las mejores constantes para la energía de Dirichlet de una membrana n-dimensional. Específicamente, $π$ es la mayor constante tal que

{displaystyle pi leq {frac {left(int _{G}|nabla u|^{2}right)^{1/2}}{left(int _{G}|u|^{2}right)^{1/2}}}}

para todos los subconjuntos convexos $G$ de $R n$ de diámetro 1 y funciones integrables al cuadrado u en $G$ de media cero. Así como la desigualdad de Wirtinger es la forma variacional del problema de valores propios de Dirichlet en una dimensión, la desigualdad de Poincaré es la forma variacional del problema de valores propios de Neumann, en cualquier dimensión.

Transformada de Fourier y principio de incertidumbre de Heisenberg

Una animación de una geodésica en el grupo Heisenberg

La constante $π$ también aparece como un parámetro espectral crítico en la transformada de Fourier. Esta es la transformación integral, que toma una función integrable de valor complejo $f$ en la línea real a la función definida como:

{displaystyle {hat {f}}(xi)=int _{-infty }^{infty }f(x)e^{-2pi ixxi },dx.}

Aunque existen varias convenciones diferentes para la transformada de Fourier y su inversa, cualquier convención de este tipo debe incluir $π$ en alguna parte . La anterior es la definición más canónica, sin embargo, proporciona el operador unitario único en $L 2$ que también es un homomorfismo de álgebra de $L 1$ a $L \infty$ .

El principio de incertidumbre de Heisenberg también contiene el número $π$ . El principio de incertidumbre da un límite inferior definido en la medida en que es posible localizar una función tanto en el espacio como en la frecuencia: con nuestras convenciones para la transformada de Fourier,

{displaystyle left(int _{-infty }^{infty }x^{2}|f(x)|^{2},dxright)left(int _{-infty }^{infty }xi ^{2}|{hat {f}}(xi)|^{2},dxi right)geq left({frac {1}{4pi }}int _{-infty }^{infty }|f(x)|^{2},dxright)^{2}.}

La consecuencia física, sobre la incertidumbre en las observaciones simultáneas de posición y momento de un sistema mecánico cuántico, se analiza a continuación. La aparición de $π$ en las fórmulas del análisis de Fourier es, en última instancia, una consecuencia del teorema de Stone-von Neumann, que afirma la unicidad del Representación de Schrödinger del grupo de Heisenberg.

Integrales de Gauss

Un gráfico de la función gaissa

. () x) e - x 2

. La región de colores entre la función y la x-eje tiene área

\sqrt π

Los campos de probabilidad y estadística utilizan con frecuencia la distribución normal como un modelo simple para fenómenos complejos; por ejemplo, los científicos generalmente asumen que el error de observación en la mayoría de los experimentos sigue una distribución normal. La función gaussiana, que es la función de densidad de probabilidad de la distribución normal con media $μ$ y desviación estándar $σ$ , naturalmente contiene π:

{displaystyle f(x)={1 over sigma {sqrt {2pi }}},e^{-(x-mu)^{2}/(2sigma ^{2})}.}

El factor de ${displaystyle {tfrac {1}{sqrt {2pi }}}}$ hace que el área bajo el gráfico de $f$ igual a uno, como se requiere para una distribución de probabilidad. Esto se deriva de un cambio de variables en la integral gausiana:

{displaystyle int _{-infty }^{infty }e^{-u^{2}},du={sqrt {pi }}}

que dice que el área bajo la curva de campana básica en la figura es igual a la raíz cuadrada de $π$ .

El teorema del límite central explica el papel central de las distribuciones normales y, por lo tanto, de $π$ , en probabilidad y estadística. Este teorema está conectado en última instancia con la caracterización espectral de $π$ como el valor propio asociado con el principio de incertidumbre de Heisenberg, y el hecho de que se cumple la igualdad en el principio de incertidumbre solo para la función gaussiana. De manera equivalente, $π$ es la única constante que hace que la distribución normal gaussiana $e -π x 2$ igual a su propia transformada de Fourier. De hecho, según Howe (1980), el "todo el asunto" de establecer los teoremas fundamentales del análisis de Fourier se reduce a la integral de Gauss.

Geometría proyectiva

Vamos $V$ ser el conjunto de todas las dos veces diferentes funciones reales ${displaystyle f:mathbb {R} to mathbb {R} }$ que satisfacen la ecuación diferencial ordinaria ${displaystyle f''(x)+f(x)=0}$ . Entonces... $V$ es un espacio vectorial real bidimensional, con dos parámetros correspondientes a un par de condiciones iniciales para la ecuación diferencial. Para cualquier $tin {mathbb R}$ , vamos ${displaystyle e_{t}:Vto mathbb {R} }$ ser la evaluación funcional, que se asocia a cada ${displaystyle fin V}$ el valor ${displaystyle e_{t}(f)=f(t)}$ de la función $f$ en el punto real $t$ . Entonces, para cada uno t, el núcleo de $e_t$ es un subespacio lineal unidimensional $V$ . Por lo tanto ${displaystyle tmapsto ker e_{t}}$ define una función desde ${displaystyle mathbb {R} to mathbb {P} (V)}$ desde la línea real hasta la línea de proyecto real. Esta función es periódica y la cantidad $π$ se puede caracterizar como el período de este mapa.

Topología

Uniformización del cuartic Klein, una superficie del género tres y la característica Euler −4, como un cociente del plano hiperbólico por el grupo de simetría PSL(2,7) del plano Fano. El área hiperbólica de un dominio fundamental es

8π

, por Gauss–Bonnet.

La constante $π$ aparece en la fórmula de Gauss-Bonnet que relaciona la geometría diferencial de las superficies con su topología. Específicamente, si una superficie compacta $Σ$ tiene una curvatura de Gauss K, entonces

{displaystyle int _{Sigma }K,dA=2pi chi (Sigma)}

donde $χ (Σ)$ es la característica de Euler, que es un número entero. Un ejemplo es el área superficial de una esfera S de curvatura 1 (de modo que su radio de curvatura, que coincide con su radio, también es 1). La característica de Euler de una esfera se puede calcular a partir de su grupos de homología y se encuentra que es igual a dos. Así tenemos

{displaystyle A(S)=int _{S}1,dA=2pi cdot 2=4pi }

reproduciendo la fórmula del área superficial de una esfera de radio 1.

La constante aparece en muchas otras fórmulas integrales en topología, en particular, aquellas que involucran clases características a través del homomorfismo de Chern-Weil.

Cálculo vectorial

Decomposiciones de armónicos esféricos, un área en cálculo vectorial

El cálculo vectorial es una rama del cálculo que se ocupa de las propiedades de los campos vectoriales y tiene muchas aplicaciones físicas, como la electricidad y el magnetismo. El potencial newtoniano para una fuente puntual $Q$ situada en el origen de un sistema de coordenadas cartesianas tridimensional es

{displaystyle V(mathbf {x})=-{frac {kQ}{|mathbf {x} |}}}

que representa la energía potencial de una unidad de masa (o carga) colocada a una distancia $| x |$ de la fuente y $k$ es una constante dimensional. El campo, denotado aquí por $E$ , que puede ser el campo gravitatorio (newtoniano) o el campo eléctrico (culombio), es el gradiente negativo de la potencial:

{displaystyle mathbf {E} =-nabla V.}

Los casos especiales incluyen la ley de Coulomb y la ley de gravitación universal de Newton. Gauss' La ley establece que el flujo hacia afuera del campo a través de cualquier superficie suave, simple, cerrada y orientable $S$ que contiene el origen es igual a $4 π kQ$ :

{displaystyle 4pi kQ=}

{scriptstyle S}

{displaystyle mathbf {E} cdot dmathbf {A}.}

Es estándar absorber este factor de $4π$ en la constante $k$ , en cuyo caso aparece en el numerador de la ecuación del potencial. Este argumento muestra por qué debe aparecer en alguna parte. Además, $4π$ es el área de superficie de la esfera unitaria, pero no hemos asumido que $S$ es la esfera. Sin embargo, como consecuencia del teorema de la divergencia, debido a que la región que se aleja del origen es el vacío (sin fuente), solo es la clase de homología de la superficie $S$ en $R 3 ∖ {0}$ que importa al calcular la integral, por lo que puede ser reemplazada por cualquier superficie conveniente en la misma clase de homología, en particular, una esfera, donde las coordenadas esféricas pueden usarse para calcular la integral.

Una consecuencia de la ley de Gauss es que el Laplaciano negativo del potencial $V$ es igual a $4π kQ$ veces la función delta de Dirac:

{displaystyle Delta V(mathbf {x})=-4pi kQdelta (mathbf {x}).}

A partir de esto se obtienen distribuciones más generales de materia (o carga) por convolución, dando la ecuación de Poisson

{displaystyle Delta V(mathbf {x})=-4pi krho (mathbf {x})}

donde $ρ$ es la función de distribución.

La constante $π$ también juega un papel análogo en los potenciales de cuatro dimensiones asociados con las ecuaciones de Einstein, una función fundamental fórmula que forma la base de la teoría general de la relatividad y describe la interacción fundamental de la gravitación como resultado de la curvatura del espacio-tiempo por la materia y la energía:

{displaystyle R_{mu nu }-{frac {1}{2}}Rg_{mu nu }+Lambda g_{mu nu }={frac {8pi G}{c^{4}}}T_{mu nu },}

Donde $R μ$ es el tensor de curvatura Ricci, $R$ es la curvatura del cuero cabelludo, $g μ$ es el tensor métrico, $▪$ es la constante cosmológica, $G$ es la constante gravitacional de Newton, $c$ es la velocidad de la luz en el vacío, y $T μ$ es el tensor de la energía. El lado izquierdo de la ecuación de Einstein es un análogo no lineal del Laplaciano del tensor métrico, y se reduce a eso en el límite de campo débil, con el ${displaystyle Lambda g}$ término que juega el papel de un multiplicador Lagrange, y el lado derecho es el análogo de la función de distribución, tiempos $8π$ .

Fórmula integral de Cauchy

Las funciones analíticas complejas se pueden visualizar como una colección de aerosoles y equipostentiales, sistemas de curvas que intersectan en ángulos rectos. Aquí ilustrado es el logaritmo complejo de la función Gamma.

Una de las herramientas clave en el análisis complejo es la integración del contorno de una función sobre una curva de Jordan positivamente orientada (rectificable) $γ$ . Una forma de la fórmula integral de Cauchy establece que si un punto $z 0$ es interior a γ, luego

{displaystyle oint _{gamma }{frac {dz}{z-z_{0}}}=2pi i.}

Aunque la curva $γ$ no es un círculo y, por lo tanto, no tiene ninguna conexión obvia con la constante $π$ , una prueba estándar de este resultado utiliza el teorema de Morera, que implica que la integral es invariante bajo homotopía de la curva, por lo que puede deformarse en un círculo y luego integrarse explícitamente en coordenadas polares. Más generalmente, es cierto que si una curva cerrada rectificable $γ$ no contiene $z 0$ , entonces la integral anterior es $2π i$ veces el número de vueltas de la curva.

La forma general de la fórmula integral de Cauchy establece la relación entre los valores de una función analítica compleja $f (z)$ en la curva de Jordan $γ$ y el valor de $f (z)$ en cualquier punto interior $z 0$ de $γ:$

{displaystyle oint _{gamma }{f(z) over z-z_{0}},dz=2pi if(z_{0})}

siempre que $f (z)$ sea analítico en la región delimitada por $γ$ y se extiende continuamente a $γ$ . La fórmula integral de Cauchy es un caso especial del teorema del residuo, que si $g (z)$ es un función meromórfica la región encerrada por $γ$ y es continua en una vecindad de $γ$ , entonces

{displaystyle oint _{gamma }g(z),dz=2pi isum operatorname {Res} (g,a_{k})}

donde la suma es de los residuos en los polos de $g (z)$ .

La función gamma y la aproximación de Stirling

Parcela de la función gamma en el eje real

Función factorial $n!$ es el producto de todos los enteros positivos a través de $n$ . La función gamma extiende el concepto de factorial (normalmente definido sólo para los números no negativos) a todos los números complejos, excepto los números negativos reales, con la identidad ${displaystyle Gamma (n)=(n-1)!}$ . Cuando se evalúa la función gamma a medio número, el resultado contiene $π$ . Por ejemplo, $Gamma (1/2)={sqrt {pi }}$ y ${textstyle Gamma (5/2)={frac {3{sqrt {pi }}}{4}}}$ .

La función gamma se define por el desarrollo de su producto Weierstrass:

{displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{n=1}^{infty }{frac {e^{z/n}}{1+z/n}}}

donde $γ$ es la constante de Euler-Mascheroni. Evaluada en $z = 1/2$ y elevada al cuadrado, la ecuación $Γ(1/2) 2 = π$ se reduce a la fórmula del producto Wallis. La función gamma también está conectada con la función zeta de Riemann y las identidades del determinante funcional, en el que la constante $π$ juega un papel importante.

La función gamma se usa para calcular el volumen $V n (r)$ de la bola n-dimensional de radio r en el espacio euclidiano n-dimensional, y el área superficial $S n -1 (r)$ de su límite, el (n−1)-dimensional esfera:

{displaystyle V_{n}(r)={frac {pi ^{n/2}}{Gamma left({frac {n}{2}}+1right)}}r^{n},}

{displaystyle S_{n-1}(r)={frac {npi ^{n/2}}{Gamma left({frac {n}{2}}+1right)}}r^{n-1}.}

Además, de la ecuación funcional se sigue que

{displaystyle 2pi r={frac {S_{n+1}(r)}{V_{n}(r)}}.}

La función gamma se puede utilizar para crear una simple aproximación a la función factorial $n!$ para grandes $n$ : ${textstyle n!sim {sqrt {2pi n}}left({frac {n}{e}}right)^{n}}$ que se conoce como la aproximación de Stirling. Equivalentemente,

{displaystyle pi =lim _{nto infty }{frac {e^{2n}n!^{2}}{2n^{2n+1}}}.}

Como una aplicación geométrica de la aproximación de Stirling, sea $Δ n$ el símplex estándar en n-dimensional, y $(n + 1)Δ n$ denota el símplex que tiene todos sus lados escalados por un factor de $n + 1$ . Después

{displaystyle operatorname {Vol} ((n+1)Delta _{n})={frac {(n+1)^{n}}{n!}}sim {frac {e^{n+1}}{sqrt {2pi n}}}.}

La conjetura de volumen de Ehrhart es que este es el límite superior (óptimo) del volumen de un cuerpo convexo que contiene solo un punto de red.

Teoría de números y función zeta de Riemann

Cada primo tiene un grupo Prüfer asociado, que son localizaciones aritméticas del círculo. Las funciones L de la teoría de números analíticos también se localizan en cada primera p.

Solución del problema de Basilea utilizando la conjetura Weil: el valor de

Especificaciones 2)

es el área hiperbólica de un dominio fundamental del grupo modular, tiempos

π /2

La función zeta de Riemann $ζ (s)$ se utiliza en muchas áreas de las matemáticas. Cuando se evalúa en $s = 2$ se puede escribir como

{displaystyle zeta (2)={frac {1}{1^{2}}}+{frac {1}{2^{2}}}+{frac {1}{3^{2}}}+cdots }

Encontrar una solución simple para esta serie infinita fue un famoso problema matemático llamado el problema de Basilea. Leonhard Euler lo resolvió en 1735 cuando demostró que era igual a $π 2 /6$ . El resultado de Euler conduce al resultado de la teoría de números de que la probabilidad de que dos números aleatorios sean primos relativos (es decir, que no tengan factores compartidos) es igual a $6/π 2$ . Esta probabilidad se basa en la observación de que la probabilidad de que cualquier número sea divisible por un primo $p$ es $1/ p$ (por ejemplo, cada séptimo entero es divisible por 7). Por lo tanto, la probabilidad de que dos números sean ambos divisibles por este número primo es $1/ p 2$ , y la probabilidad de que al menos uno de ellos no lo sea es $1 - 1/ p 2$ . Para primos distintos, estos eventos de divisibilidad son mutuamente independientes; por lo que la probabilidad de que dos números sean primos relativos viene dada por un producto de todos los números primos:

{displaystyle {begin{aligned}prod _{p}^{infty }left(1-{frac {1}{p^{2}}}right)&=left(prod _{p}^{infty }{frac {1}{1-p^{-2}}}right)^{-1}\[4pt]&={frac {1}{1+{frac {1}{2^{2}}}+{frac {1}{3^{2}}}+cdots }}\[4pt]&={frac {1}{zeta (2)}}={frac {6}{pi ^{2}}}approx 61%.end{aligned}}}

Esta probabilidad se puede usar junto con un generador de números aleatorios para aproximar $π$ usando un enfoque de Monte Carlo.

La solución al problema de Basilea implica que la cantidad derivada geométricamente $π$ está profundamente conectada con la distribución de números primos números. Este es un caso especial de la conjetura de Weil sobre los números de Tamagawa, que afirma la igualdad de tales productos infinitos similares de cantidades aritméticas, localizados en cada primo p, y una cantidad geométrica: el recíproco del volumen de cierto espacio localmente simétrico. En el caso del problema de Basilea, es la triple variedad hiperbólica $SL2(R)/SL2(Z)$ .

La función zeta también satisface la ecuación funcional de Riemann, que involucra tanto $π$ como la función gamma:

{displaystyle zeta (s)=2^{s}pi ^{s-1} sin left({frac {pi s}{2}}right) Gamma (1-s) zeta (1-s).}

Además, la derivada de la función zeta satisface

{displaystyle exp(-zeta '(0))={sqrt {2pi }}.}

Una consecuencia es que $π$ se puede obtener a partir del determinante funcional del oscilador armónico. Este determinante funcional se puede calcular a través de una expansión del producto y es equivalente a la fórmula del producto de Wallis. El cálculo se puede reformular en mecánica cuántica, específicamente el enfoque variacional del espectro del átomo de hidrógeno.

Serie de Fourier

π

aparece en caracteres de números p-adic (shown), que son elementos de un grupo Prüfer. La tesis de Tate hace un uso pesado de esta maquinaria.

La constante $π$ También aparece naturalmente en la serie Fourier de funciones periódicas. Funciones periódicas son funciones del grupo $T = R / Z$ de partes fraccionadas de números reales. La descomposición de Fourier muestra que una función de valor complejo $f$ on $T$ puede ser escrito como una superposición lineal infinita de caracteres unitarios $T$ . Es decir, homomorfismos de grupo continuos de $T$ al grupo círculo $U 1)$ de los números complejos del módulo de unidad. Es un teorema que cada carácter de $T$ es uno de los exponenciales complejos ${displaystyle e_{n}(x)=e^{2pi inx}}$ .

Hay un carácter único en $T$ , hasta conjugación compleja, que es un isomorfismo de grupo. Utilizando la medida de Haar en el grupo circular, la constante $π$ es la mitad de la magnitud de la derivada Radon-Nikodym de este carácter. Los otros caracteres tienen derivadas cuyas magnitudes son múltiplos enteros positivos de 2 $π$ . Como resultado, la constante $π$ es el único número tal que el grupo T, equipado con su Haar medida, es Pontrjagin dual a la red de múltiplos enteros de 2 $π$ . Esta es una versión de la fórmula de suma de Poisson unidimensional.

Formas modulares y funciones theta

Las funciones Theta se transforman bajo la celosía de los períodos de una curva elíptica.

La constante $π$ está profundamente conectada con la teoría de formas modulares y funciones theta. Por ejemplo, el algoritmo de Chudnovsky involucra de manera esencial la j-invariante de una curva elíptica.

Las formas modulares son funciones holomorfas en el medio plano superior caracterizadas por sus propiedades de transformación bajo el grupo modular ${displaystyle mathrm {SL} _{2}(mathbb {Z})}$ (o sus diversos subgrupos), una celosía en el grupo ${displaystyle mathrm {SL} _{2}(mathbb {R})}$ . Un ejemplo es la función Jacobi theta

{displaystyle theta (z,tau)=sum _{n=-infty }^{infty }e^{2pi inz+ipi n^{2}tau }}

que es una especie de forma modular llamada forma Jacobi. Esto a veces se escribe en términos de la nome $q=e^{pi i tau}$ .

La constante $π$ es la única constante que hace que la función theta de Jacobi tenga una forma automórfica, lo que significa que se transforma en una forma específica forma. Ciertas identidades se mantienen para todas las formas automórficas. un ejemplo es

{displaystyle theta (z+tautau)=e^{-pi itau -2pi iz}theta (z,tau),}

lo que implica que $θ$ se transforma como una representación bajo el grupo discreto de Heisenberg. Las formas modulares generales y otras funciones theta también implican $π$ , una vez más debido al teorema de Stone-von Neumann.

Distribución de Cauchy y teoría del potencial

La Bruja de Agnesi, llamada por María Agnesi (1718-1799), es una construcción geométrica del gráfico de la distribución Cauchy.

La distribución Cauchy rige el paso de partículas marrones a través de una membrana.

La distribución de Cauchy

{displaystyle g(x)={frac {1}{pi }}cdot {frac {1}{x^{2}+1}}}

es una función de densidad de probabilidad. La probabilidad total es igual a uno, debido a la integral:

{displaystyle int _{-infty }^{infty }{frac {1}{x^{2}+1}},dx=pi.}

La entropía de Shannon de la distribución de Cauchy es igual a $ln(4π)$ , que también implica $π$ .

La distribución de Cauchy juega un papel importante en la teoría del potencial porque es la medida de Furstenberg más simple, el núcleo de Poisson clásico asociado con un movimiento browniano en un semiplano. Las funciones armónicas conjugadas y, por lo tanto, también la transformada de Hilbert están asociadas con las asintóticas del núcleo de Poisson. La transformada de Hilbert H es la transformada integral dada por el valor principal de Cauchy de la integral singular

{displaystyle Hf(t)={frac {1}{pi }}int _{-infty }^{infty }{frac {f(x),dx}{x-t}}.}

La constante $π$ es el factor de normalización único (positivo) tal que H define un estructura compleja en el espacio de Hilbert de funciones de valor real integrables al cuadrado en la recta real. La transformada de Hilbert, como la transformada de Fourier, se puede caracterizar únicamente en términos de sus propiedades de transformación en el espacio de Hilbert $L 2 (R)$ : hasta un factor de normalización, es el único operador lineal acotado que conmuta con dilataciones positivas y anticonmuta con todas las reflexiones de la recta real. La constante $π$ es el único factor de normalización que hace que esta transformación sea unitaria.

En el conjunto de Mandelbrot

El conjunto Mandelbrot se puede utilizar para aproximar

π

David Boll descubrió en 1991 una ocurrencia de $π$ en el fractal llamado conjunto de Mandelbrot. Examinó el comportamiento de el conjunto de Mandelbrot cerca del "cuello" en $(-0.75, 0)$ . Cuando el número de iteraciones hasta la divergencia del punto $(-0.75, ε)$ se multiplica por $ε$ , el resultado se acerca a $π$ como estilo $ε$ tiende a cero. El punto $(0.25 + ε, 0)$ en la cúspide del gran "valle" en el lado derecho del conjunto de Mandelbrot se comporta de manera similar: el número de iteraciones hasta la divergencia multiplicado por la raíz cuadrada de $ε$ tiende a $π$ .

Afuera de las matemáticas

Describir fenómenos físicos

Aunque no es una constante física, $π$ aparece habitualmente en ecuaciones que describen los principios fundamentales del universo, a menudo debido a $Relación de π$ con el círculo y con los sistemas de coordenadas esféricas. Una fórmula simple del campo de la mecánica clásica da el período aproximado $T$ de un péndulo simple de longitud $L$ , oscilando con una pequeña amplitud ( $g$ es la aceleración gravitacional de la tierra):

{displaystyle Tapprox 2pi {sqrt {frac {L}{g}}}.}

Una de las fórmulas clave de la mecánica cuántica es el principio de incertidumbre de Heisenberg, que muestra que la incertidumbre en la medición de la posición de una partícula (Δ $x$ ) y el impulso (Δ $p$ ) no pueden ser arbitrariamente pequeños al mismo tiempo (donde $h$ es la constante de Planck):

{displaystyle Delta x,Delta pgeq {frac {h}{4pi }}.}

El hecho de que $π$ sea aproximadamente igual a 3 juega un papel en la vida útil relativamente larga del ortopositronio. El tiempo de vida inverso al orden más bajo en la constante de estructura fina $α$ es

{displaystyle {frac {1}{tau }}=2{frac {pi ^{2}-9}{9pi }}malpha ^{6},}

donde $m$ es la masa del electrón.

$π$ está presente en algunas fórmulas de ingeniería estructural, como la fórmula de pandeo derivada de Euler, que proporciona la carga axial máxima $F$ que una columna larga y delgada de longitud $L$ , módulo de elasticidad $E$ , y el momento de inercia del área $I$ puede transportar sin pandeo:

{displaystyle F={frac {pi ^{2}EI}{L^{2}}}.}

El campo de la dinámica de fluidos contiene $π$ en Stokes' ley, que se aproxima a la fuerza de fricción $F$ ejercida sobre pequeños objetos esféricos de radio $R$ , moviéndose con velocidad $v$ en un fluido con viscosidad dinámica $η :$

{displaystyle F=6pi eta Rv.}

En electromagnetismo, la constante de permeabilidad al vacío μ₀ aparece en las ecuaciones de Maxwell, que describen las propiedades de los campos eléctricos y magnéticos y la radiación electromagnética. Antes del 20 de mayo de 2019, se definió como exactamente

{displaystyle mu _{0}=4pi times 10^{-7}{text{ H/m}}approx 1.2566370614ldots times 10^{-6}{text{ N/A}}^{2}.}

Se puede derivar una relación para la velocidad de la luz en el vacío, $c$ a partir de las ecuaciones de Maxwell en el medio del vacío clásico usando una relación entre μ₀ y la constante eléctrica (permisividad del vacío), $ε 0$ en unidades SI:

{displaystyle c={1 over {sqrt {mu _{0}varepsilon _{0}}}}.}

En condiciones ideales (pendiente suave uniforme sobre un sustrato erosionable homogéneamente), la sinuosidad de un río serpenteante se aproxima a $π$ . La sinuosidad es la relación entre la longitud real y la distancia en línea recta desde la fuente hasta la boca. Las corrientes más rápidas a lo largo de los bordes exteriores de las curvas de un río causan más erosión que a lo largo de los bordes interiores, lo que empuja las curvas aún más hacia afuera y aumenta la curvatura general del río. Sin embargo, ese bucle eventualmente hace que el río se doble sobre sí mismo en algunos lugares y haga un "cortocircuito", creando un lago en forma de meandro en el proceso. El equilibrio entre estos dos factores opuestos conduce a una relación promedio de $π$ entre la longitud real y la distancia directa entre la fuente y la boca.

Memorización de dígitos

La pifilología es la práctica de memorizar un gran número de dígitos de $π$ , y los registros mundiales los mantiene el Récords mundiales Guinness. El récord de memorización de dígitos de $π$ , certificado por Guinness World Records, es de 70 000 dígitos, recitado en India por Rajveer Meena en 9 horas y 27 minutos el 21 de marzo de 2015. En 2006, Akira Haraguchi, un ingeniero japonés jubilado, afirmó haber recitado 100.000 decimales, pero Guinness World Records no verificó la afirmación.

Una técnica común es memorizar una historia o un poema en el que la longitud de las palabras represente los dígitos de $π$ : la primera palabra tiene tres letras, la segunda palabra tiene una, la tercera tiene cuatro, la cuarta tiene una, la quinta tiene cinco, y así sucesivamente. Estas ayudas para la memorización se denominan mnemónicos. Un ejemplo temprano de un mnemotécnico para pi, ideado originalmente por el científico inglés James Jeans, es "Cómo quiero un trago, alcohólico, por supuesto, después de las pesadas conferencias sobre mecánica cuántica". Cuando se usa un poema, a veces se le llama piem. Se han compuesto poemas para memorizar $π$ en varios idiomas además del inglés. Los memorizadores $π$ que establecen récords normalmente no se basan en poemas, sino que utilizan métodos como recordar patrones numéricos y el método de loci.

Algunos autores han utilizado los dígitos de $π$ para establecer una nueva forma de escritura restringida, donde se requiere la longitud de las palabras para representar los dígitos de $π$ . La Cadaeic Cadenza contiene los primeros 3835 dígitos de $π$ de esta manera, y el libro completo Not a Wake contiene 10 000 palabras, cada una de las cuales representa un dígito de $π$ .

En la cultura popular

Un pastel de pipa. Las piezas son circulares, y "pie" y

π

son homófonos, haciendo tarta un tema frecuente de pi puns.

Quizás debido a la simplicidad de su definición y su presencia omnipresente en las fórmulas, $π$ se ha representado en la cultura popular más de otras construcciones matemáticas.

En la coproducción del documental de la Open University y la BBC de 2008, La historia de las matemáticas, que se emitió en octubre de 2008 en BBC Four, el matemático británico Marcus du Sautoy muestra una visualización del, históricamente el primer exacto: fórmula para calcular π al visitar la India y explorar sus contribuciones a la trigonometría.

En el Palais de la Découverte (un museo de ciencias de París) hay una sala circular conocida como la sala pi. En su pared hay inscritos 707 dígitos de $π$ . Los dígitos son grandes caracteres de madera adheridos al techo en forma de cúpula. Los dígitos se basaron en un cálculo de 1873 realizado por el matemático inglés William Shanks, que incluía un error que comenzaba en el dígito 528. El error fue detectado en 1946 y corregido en 1949.

En la novela Contacto de Carl Sagan de 1985, se sugiere que el creador del universo enterró un mensaje en lo profundo de los dígitos de $π$ . Los dígitos de $π$ también se han incorporado a la letra de la canción "Pi" del álbum de 2005 Aerial de Kate Bush. En el episodio "Wolf in the Fold" de Star Trek de 1967, se contiene una computadora fuera de control al recibir instrucciones de "Calcular hasta el último dígito el valor de $π$ ".

En Estados Unidos, el Día Pi cae el 14 de marzo (escrito 3/14 al estilo estadounidense) y es popular entre los estudiantes. $π$ y su representación digital a menudo son utilizados por autodenominados "geeks matemáticos" para bromas internas entre grupos de mentalidad matemática y tecnológica. Una alegría universitaria atribuida de diversas formas al Instituto Tecnológico de Massachusetts o al Instituto Politécnico Rensselaer incluye "3.14159". El Día Pi en 2015 fue particularmente significativo porque la fecha y la hora 14/03/15 9:26:53 reflejaron muchos más dígitos de pi. En partes del mundo donde las fechas se anotan comúnmente en formato de día/mes/año, el 22 de julio representa el 'Día de aproximación de Pi', como 22/7 = 3,142857.

Durante la subasta de 2011 de la cartera de valiosas patentes tecnológicas de Nortel, Google realizó una serie de ofertas inusualmente específicas basadas en constantes matemáticas y científicas, incluidas $π$ .

En 1958, Albert Eagle propuso reemplazar $π$ por $τ$ (tau), donde $τ = π /2$ , para simplificar fórmulas, pero este uso de $τ$ es por lo demás desconocido. Algunos proponen τ = 2π, argumentando que $τ$ , como el número de radianes en una vuelta o la relación de un círculo' s circunferencia a su radio, es más natural que $π$ y simplifica muchas fórmulas. Este uso de $τ$ no ha llegado a la corriente principal de las matemáticas, pero se ha agregado a varios lenguajes de programación como una constante predefinida.

En 1897, un matemático aficionado intentó persuadir a la legislatura de Indiana para que aprobara el proyecto de ley Pi de Indiana, que describía un método para cuadrar el círculo y contenía texto que implicaba varios valores incorrectos para $π$ , incluido 3.2. El proyecto de ley es notorio como un intento de establecer un valor de constante matemática por decreto legislativo. El proyecto de ley fue aprobado por la Cámara de Representantes de Indiana, pero rechazado por el Senado, lo que significa que no se convirtió en ley.

En la cultura informática

En la cultura contemporánea de Internet, las personas y las organizaciones suelen rendir homenaje al número $π$ . Por ejemplo, el científico informático Donald Knuth permitió que los números de versión de su programa TeX se acercaran a $π$ . Las versiones son 3, 3.1, 3.14, etc.

Contenido relacionado

Más resultados...

Pi